基于Burg法的城市轨道交通快速线路轨道不平顺谱研究

2020-05-29崔旭浩

铁道学报 2020年4期

金锋,肖宏,崔旭浩

(北京交通大学轨道工程北京市重点实验室，北京 100044)

轨道不平顺是轨道结构的基本属性之一，与轮轨间非线性接触状态密切相关，是线路设计的基本输入参数。截至2019年9月，我国已有39个城市开通城市轨道交通线路，尽管运营里程已超过6 000 km,但至今我国尚未建立通用的城市轨道交通不平顺谱。而根据新一轮北京轨道交通线网规划(2017—2035年),我国将稳步推进快速、大规模修建城市轨道交通线路的步伐。可见，基于采集的大量轨检数据开展城市轨道交通不平顺谱研究，不仅重要而且紧迫。

近年来，随着城市规模的不断扩张，部分城市轨道交通线路的速度也大幅提升，其中北京地铁6号线的速度最高可达100 km/h。北京地铁6号线首次采用8节B型地铁列车并使用接触网供电方式，是首次采用100 km/h列车的市区主干线，是第一条采用快慢车且设置快车越行站的线路。以往城市轨道交通在低速状态下可以采用铁路干线谱、国外谱等进行保守设计，然而随着速度的增加，半径小、速度高的动力特征就愈发显著。如果还采用传统的轨道谱进行设计，不仅会引起轨道零部件伤损，如扣件折断[1]等，严重时设计的线路还会直接影响列车的运营安全。因此，对城市轨道交通快速线进行深入研究并建立对应的轨道谱，对我国轨道交通建设具有非常重要的意义。

针对轨道不平顺谱，国内外已开展了相关研究。文献[2]分析了沪宁线不平顺谱的特征，并使用相干分析的方法进行了影响车辆加速度不平顺因素的辨别。文献[3]提出一种新的窗函数，一定程度上缓解了谱估计过程中的边界效应。文献[4]分析了钢轨接头处的不平顺功率谱，并使用了小波分析方法。文献[5]通过对大量基础数据的总结提出了中国干线铁路通用轨道谱。文献[6]对朔黄重载铁路进行了不平顺谱的估计，并使用HHT(Hilbert-Huang Transform)从时域与频域上进行了轨道不平顺幅值能量的分析。国外谱如美国六级谱[7]与德国干扰谱[8]，更是广泛应用于相关的设计与研究工作之中。

综上可以看出，通过不断研究[9-13]，已经获得不同类型的轨道谱，包括高速铁路谱、客运专线谱、冻胀地区轨道谱、重载铁路谱等。但至今，我国尚未建立轨道交通不平顺谱，尤其是轨道交通快速线路谱，这严重影响了轨道交通的合理设计、检测评估，并大大阻碍了轨道新产品、新技术的研发与推广。

因此，本文以综合轨检车测量的北京地铁6号线正常状态几何形位检测数据为基础，通过多尺度小波分析及异常值剔除算法，引入并推导现代谱估计中的Burg法，进行城市轨道交通快速线路不平顺谱研究。

1 不平顺数据预处理

由于人工标定、传感器漂移、数据传输、天气等原因，会导致轨检车进行轨检作业时获取的轨检数据存在明显的异常值，为了消除数据异常值的影响，需要针对轨道不平顺的特性选择适宜的滤波算法进行轨检数据的预处理。

1.1 异常值剔除算法

使用逐点遍历法对原始轨检车检测数据进行异常值剔除。与相邻值比较法相比，逐点遍历法解决了出现连续多个超限不平顺幅值时方法失效的问题。

图1为逐点遍历法剔值处理后与原始输入数据的对比图。从图1可以看出，使用该方法进行异常值消除的效果比较明显，有效地剔除了错误项。

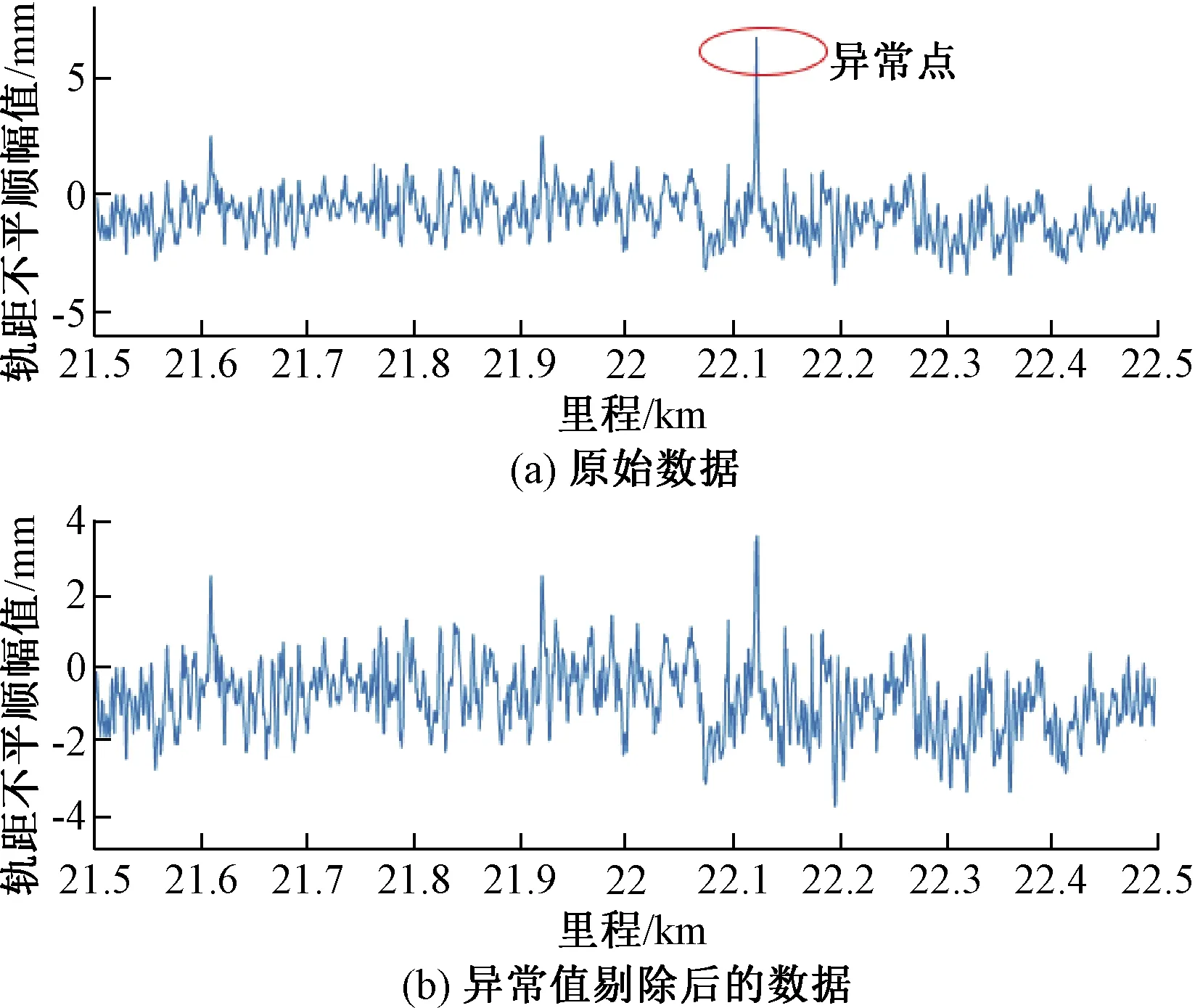
图1 异常值剔除后与原始数据对比

1.2 多尺度趋势项消除算法

轨距、轨向等不平顺由于其结构特性，存在明显的趋势项，其均值不为0，从图1就可以看出图形中轴趋于负值，这也说明需要进行趋势项的消除。

考虑到轨检车采样过程中信号频率范围较宽，且不是严格的周期信号，本文采用小波分析方法进行多尺度趋势项消除。

1.2.1 多尺度趋势项消除算法

正交小波变换中用到两个滤波器组h(j)与g(j)，分别表示低通滤波器与高通滤波器，两者关系为g(j)=(-1)jh(1-k)。令需要处理的信号f(j)为原始信号，且取a0(j)=f(j)，则信号分解、重构算法[14]为

(1)

(2)

(3)

式中：i为分解次数。式(1)、式(2)为分解算法，式(3)为重构算法，通过分解可将实测轨道不平顺数据中低频成分与高频成分分离开来，其中所需要的不平顺数据为高频部分，低频部分则为曲线超高等的趋势项，在重构过程中将低频信号选择性地过滤可达到消除趋势项的目的。

对于理想滤波器，在2j尺度上，h(f)和g(f)的频率范围分别为[0,fs/2j+1]和(fs/2j+1,fs/2j]，轨检车每隔0.25 m采样一次，采样空间频率fs为4，而我们所关注的轨道谱中主要不平顺波长范围为1～32 m，需要分解6次才能达到滤波目的。考虑到轨道结构的特殊性，需要对小波分析所使用的小波基进行严格的筛选与对比。

1.2.2 小波基选取对比

在小波分析的过程中扮演最重要角色的就是小波基，目前较为流行的有正交小波Daubechies小波(dbN)、双正交小波Biorthogonal(biorN.N)、近似对称的Symlet小波(symN)和Coiflet小波(coifN)等。其中N为小波分解层数，分解层数越多小波消失矩阶数越高，滤波越彻底。

为了筛选出最适合城市轨道交通滤波处理的母小波，进行了各种小波分解重构后结果的对比，见图2。

图2 各种母小波结果对比

从图2可以看出，通过小波的变换之后,基于各小波基的结果均比较明显，趋势项消除质量均满足轨道不平顺谱分析的要求。为了取最优小波基，列出相关的评价指标进行筛选，如表1所示。

表 1 小波基处理结果对比

从表1可以看出，与源数据相比，经过小波处理后数据的期望值与方差均有减小，结合图2中处理后小波的形态，可以看出对轨道谱估计有影响的低频趋势项已经被较好地处理；其次，从表1还可以看到coif5母小波的期望值与方差两个指标值均是最优。因此，本文采用coif5母小波进行趋势项消除工作。

1.2.3 趋势项消除

使用coif5小波基，进行6次多尺度分解重构得到了预处理后的轨距、高低、轨向不平顺数据。限于篇幅，仅将部分预处理结果展示，见图3。

图3 趋势项消除对比总图

从图3可以看出，轨距、高低等使用小波处理均有良好的效果，数据基线均已归零。

2 轨道谱获取方法的优化

2.1 轨道谱估计方法的选择

由于轨道不平顺影响因子众多导致其幅值的不确定性，使其有明显的随机特性。为了描述随机过程，本文使用功率谱密度(Power Spectral Density，PSD)函数进行随机过程的描述。由于获取的信号长度不为无限长，不具备平方可积条件，这对工程上使用傅里叶变换获取功率谱密度函数造成了障碍。

目前，工程上普遍使用经典谱估计方法进行轨道谱的估计。经典谱估计方法主要由周期图法与其优化方法组成。经典谱估计方法是以傅里叶分析为理论基础的一种较为成熟的谱估计方法，又称为非参数模型谱估计，包括间接法和直接法。间接法是以有限序列数据的相关函数为媒介来估计原始数据的功率谱，其理论基础是维纳-辛钦定理，在1958年由Blackman和Tukey提出[15]。作为早期的谱估计方法，间接法在延迟参数较大时会导致计算量过大，且估计的精度不高，所以一般使用直接法[16]。直接法又称周期图法，其通过直接利用有限序列数据的傅里叶变换来估计其功率谱，是经典谱估计的一个常用方法，目前所提出的中国干线谱、高速谱使用的均是周期图法或其改进方法。

直接法的方差计算十分复杂，由Jenkins 的结论[17]可知，方差可以表述为

(4)

式中:IN(ω)为直接法功率谱估计量;Px(ω)为真实功率谱;ω为圆频率;N为数据长度。当N较大时，直接法方差可近似表示为

(5)

式(5)表明，直接法的方差不随着数据量N的增大而趋于0，因此不是功率谱的一致估计[18]。

为了优化其方差性能，又提出了Bartlett法与Welch法进行轨道谱的估计。

Bartlett法基本思想是将原始数据进行分段，使用矩形窗函数进行功率谱的估计并进行平均，由于各段数据越少，估计的偏差越大，这种方法以估计的偏差增大为代价，达到减小方差的目的。

相较于Bartlett法，Welch法在进行分段时需要将每段信号样本进行重叠，在同样的分段数下各段数据变长，限制了偏差大小的范围，减小了方差，提升了经典法功率谱的估计效果。各段重叠50%可使方差减少一半，但是更多的重叠并不能进一步降低方差。

由于可使用FFT算法进行快速计算，周期图法及其优化算法广泛应用于目前轨道谱的估计，但是其具有以下缺点：

(1)经典谱分辨率较低。

(2)经典谱估计方法得到的轨道谱估计方差性能较差，不是真实轨道谱的一致估计，并且在数据点增加时谱曲线起伏加剧。

(3)经典谱估计方法的平滑和平均与窗函数的使用紧密关联。没有一个窗函数能使谱估计在方差、偏差和分辨率各方面同时得到改善，使用平滑和平均主要用来改善周期图的方差性能，但往往又降低了分辨率、增加了偏差。

(4)由于假定信号在数据观测区间以外等于0，因此估计结果较难与实际轨道谱相匹配，这种现象在数据序列较短时尤其明显，经典法不适用于短序列信号的轨道谱估计。

2.2 Burg法理论推导

经典谱估计的分辨率与信号的有效长度成反比，而现代谱估计的分辨率可以不受此限制。因为对于给定的N点有限长序列x(n)，虽然其估计出的相关函数也是有限长的，但现代谱估计方法隐含着数据和自相关函数的外推，使其可能的长度超过给定的长度，因而AR(Auto Regressive)模型谱的分辨率较高。

Burg法是AR系数求解算法中较为优秀的方法，已经逐渐应用于其他学科功率谱的估计。因此本节主要引入Burg法并进行推导，开展轨道不平顺谱估计的研究。

Burg法的基本思想是，令前后预测误差功率ρf与ρb之和为最小

(6)

计算过程中前后误差分别为ef(n)与eb(n)，这时有

(7)

(8)

上式中，当AR模型法阶次m由1增至p时，eb(n)有如下的递推关系

(9)

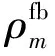
(10)

按照式(10)进行计算后，在阶次m状态下的AR模型系数可以由Levinson递推算法求出，即

(11)

在上述Burg算法的推导中可以看到，AR模型的阶数直接关系到轨道不平顺谱估计质量，若阶数太小则谱估计曲线过于平滑，若阶数太大谱估计曲线会出现虚假谱峰，图4为一段轨道不平顺数据不同阶数的对比。

因此，如何选取AR模型合适的阶数成为使用Burg法估计轨道不平顺谱的一个难点。

图4 Burg法不同阶数估计结果对比

当预测误差功率P达到指定的阈值，或者不再发生变化时，这时的阶数即是应选的正确阶数。

为了保证城市轨道交通谱对应现代谱估计阶数的科学性，使用赤池信息准则[19](Akaika’s Information theoretic Criterion，AIC)进行阶数估计。

AIC准则通过使下式达到最小估计模型阶次

(12)

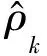
可以证明，AIC表示AR模型估计的PDF(Probability Density Function)与数据真实PDF之间的Kullback-Leibler距离的估计值，此种定阶方法不仅适用于AR模型阶次，还可用于MA(Moving Average)模型与ARMA(Auto Regressive Moving Average)模型阶次的确定[20]。

2.3 轨道谱估计质量的对比

如2.1节所述，Welch法作为周期图法的优化算法，使用加窗、数据重叠等手段减小方差。本文通过Welch法进行了轨道谱方差性能的改进。

图5为Welch法与Burg法进行谱估计的对比，从图5可以看出，Burg法相较于Welch法方差性能更好，并由于使用了与直接法、Welch法截然不同的计算手段，跳出了方差、偏差与分辨率之间的矛盾循环，在降低方差的同时，还保证了其分辨率与谱估计的准确性。

图5 Welch法与Burg法功率谱结果对比

如2.1节所述，直接法及其改进算法结果均不是实际谱的一致估计，而Burg法获取的结果则是实际谱的一致估计。Burg法与最常用的直接法、Welch法的谱估计特性比较如表2所示。

表2 不平顺谱估计方法对比

从表 2各项对比结果中可知，Burg法作为现代谱估计方法，由于计算方式的进步，相较于直接法、Welch法等经典谱估计方法在分辨率、谱的一致性、方差性能、适用范围等类别中均有优势，契合日渐提高的轨道不平顺谱估计精度与不平顺几何形位设计的需要。

3 城市轨道交通谱的拟合

根据城市轨道快速线轨道不平顺谱的分布规律及特点，通过使用计算机穷举法进行拟合公式的适应性计算，归纳、统计分析不同拟合公式，确定了适合城市轨道交通的不平顺谱拟合模型，包括轨距、高低及轨向，其表达式为

轨距：

(13)

高低：

(14)

轨向：

(15)

使用Levenberg-Marquardt最小二乘理论对Burg法得出的轨道谱估计结果进行模型参数拟合，拟合结果见图6～图8。由图6～图8可知，拟合曲线可以较好地表述基于Burg法谱估计结果的各波长段特征，其中在1～2 m小波长区段，相对而言存在少量可接受的数据拟合误差。表3为高低、轨距、轨向三种不平顺拟合的公式参数及计算结果。从表3可知，三者拟合优度均在0.95以上，拟合质量较高。

图6 轨距不平顺拟合结果

图7 高低不平顺拟合结果

图8 轨向不平顺拟合结果

表3 北京地铁6号线轨道谱拟合结果

4 城市轨道交通谱的分析

由于城市轨道交通结构本身的特殊性，其轨道不平顺也展现出不同的特性。图9～图11为城市轨道交通谱与其他谱的对比。

由图9可知，对于轨距不平顺，北京地铁快速线路谱总体上要优于美国六级谱、120 km/h通用轨道谱，劣于德国干扰谱。

图9 北京地铁6号线轨距谱与其他谱的对比

由图10可知，快速线高低谱总体上优于120 km/h通用谱，整而言趋于美国六级谱与德国低干扰谱之间，在1～6.3 m波长段要优于上海地铁谱,整体而言两者差别不大。

由图11可知，快速线轨向谱总体上优于美国六级谱、120 km/h通用谱；略优于上海地铁轨向谱，位于德国低干扰谱与德国高干扰谱之间。

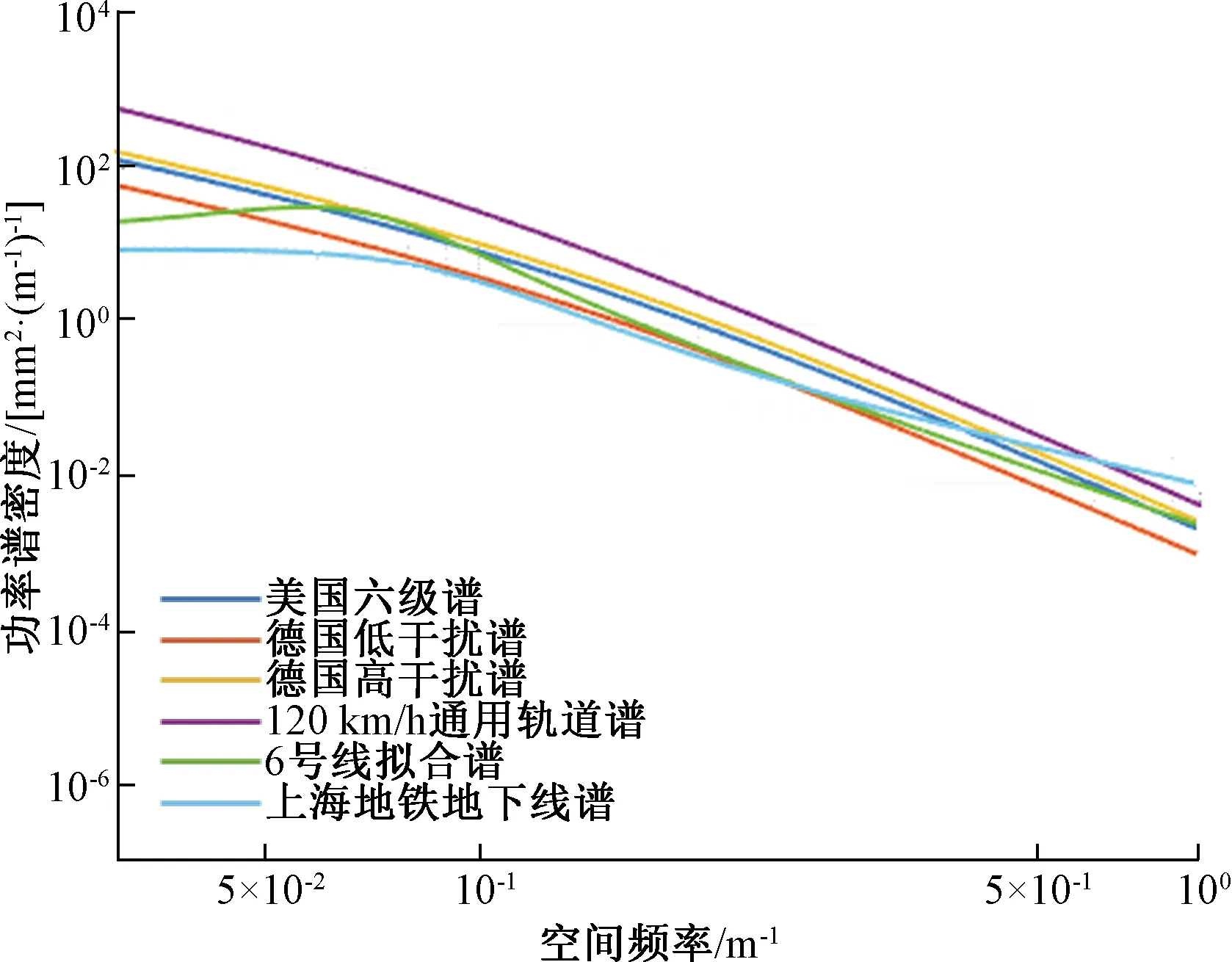
图10 北京地铁6号线高低谱与其他谱的对比

图11 北京地铁6号线轨向谱与其他谱的对比

综上可以看出，北京地铁快速线路谱优于美国六级谱、120 km/h通用谱，劣于德国低干扰谱，与上海地铁地下段谱特征相差不大。以上结果表明，城市轨道交通本身的线路特性使得其轨道谱与高速铁路谱、干线谱存在差异，而与上海地铁拟合谱相差不大，使用本文拟合谱来进行城市轨道交通尤其是快速线路的设计与研究，更接近实际、更合理。