以数学为中心的高中跨学科教学路径初探

华志远

摘要：跨学科教学是以一个学科为中心，在这个学科中选择一个题目，运用不同学科的知识，对所指向的中心题目进行加工和设计教学。实施以数学为中心的高中跨学科教学的路径有：抓住课程主线，寻求内容的交汇点;研究课程标准，寻求方法的结合点;发掘真实问题，拓展应用的边界;回顾发展历史，获得成功的经验。

关键词：高中数学;跨学科教学;科学方法;数学应用;数学史

《普通高中课程方案（2017年版）》突出了课程内容的关联性原则，即“注重学科内容选择、活动设计与学生发展核心素养养成的有机联系;关注学科间的联系与整合;增强课程内容与社会生活、高等教育和职业发展的内在联系”。但从我国高中师资现状来看，由于师范教育将教师定位于从事某一具体学科的教学工作，职后教育又较少涉及跨学科教学的培训，因此教师面临的挑战是怎样培养和发展横向联结不同领域知识的能力。

在新课改中，高中数学受关注的程度很高，但其科学、应用、人文和审美等价值远没有受到师生足够的重视，主要症结表现为教学目标过于窄化，教学过程过于封闭，较少关注与其他学科之间的联系等。对于2019年高考数学全国Ⅰ卷和Ⅱ卷中分别涉及维纳斯身高的估测和物理公式的近似推导两道题，很多学生不知所措，便是例证。

研究表明：倘若学生在数学学习中不能及时发现知识的纵横联系、实际意义和应用价值，学习兴趣就会大大降低，所学知识也会变得抽象、冰冷和乏味。而跨学科整合为数学教学开拓了新的视野，带来了新的气象。

一、理解以数学为中心的高中跨学科教学的内涵

“跨学科”概念起源于20世纪20年代，由美国学者泰勒、伍德沃斯等提出、倡导并在高等教育中实施，发展至今已有多个版本的定义。其中，笔者认为，以艾伦·雷普克给出的定义最为权威：跨学科研究是回答、解决和处理问题的进程，由于这些问题太宽泛、太复杂，仅靠单个学科的知识不足以解决;它以学科为依托，以整合见解、构建更全面的观点为目的。可见，“跨学科”概念的要素有：首先，以现实问题的研究和解决为依托;其次，以多个学科为载体，关注复杂问题或课题的全面分析与解决;再次，希望掌握明确的、整合的研究方法与思维方式;此外，力求获得新的认知，鼓励在跨学科的基础上有所发现和创新。

我国学者对跨学科教学的定义，更多地借鉴了德国学者的定义：跨学科教学是以一个学科为中心，在选择一个题目，运用不同学科的知识，对所指向的中心题目进行加工和设计教学。这一中心题目一旦被确定，就将被赋予更多的意义，即除了知识和技能目标之外，还有思想方法、思考策略以及综合素养等方面的培养。可见，跨学科教学的目标是：首先使学生有效地习得学以致用的知识，其次提高学生的能力和素养，再次引导学生形成正确的世界观、人生观和价值观。

由此延伸，以数学为中心的高中跨学科教学，是指在高中数学课程中选择合适的中心题目，运用自然科学、信息技术、社会科学、人文科学等领域的知识，对所指向的中心题目进行加工和设计教学，即以“问题链”为依托，使学生在问题（任务）的驱动下，更有效地获得知识，同时培养能力、提升素养。开展这样的教学，关键是要找到数学与其他学科整合的取向，即找到数学与其他学科之间有意义、有价值的联系，并以此为纽带对学科进行整合。

二、实施以数学为中心的高中跨学科教学的路径

（一）抓住课程主线，寻求内容的交匯点

以数学为中心的高中跨学科教学，首先，要围绕高中数学的主干知识、核心概念、定理、公式和重要思想方法展开课程内容;其次，要采用局部递进和整体贯穿的方法编排课程顺序，即每个章节的内容安排由浅入深，同时注重章节之间的衔接;再次，要结合课程内容，探寻数学与其他学科的交汇点，促进知识和方法的连接和融合。

比如，函数、方程及不等式是高中数学的主体内容，而最值又是高中数学的重点内容。对此，可以设计如下教学内容：（1）力学、热学、电磁学中的最值问题;（2）经济学、建筑学、工程学中的最优化问题;（3）其他社会生产和生活中的实际问题。这样，既能体现数学的工具性，又能体现数学结果的跨学科意义或实际意义，引发学生的拓展性讨论。

以“三角函数最值的应用”教学为例，笔者设计了以下两道例题：

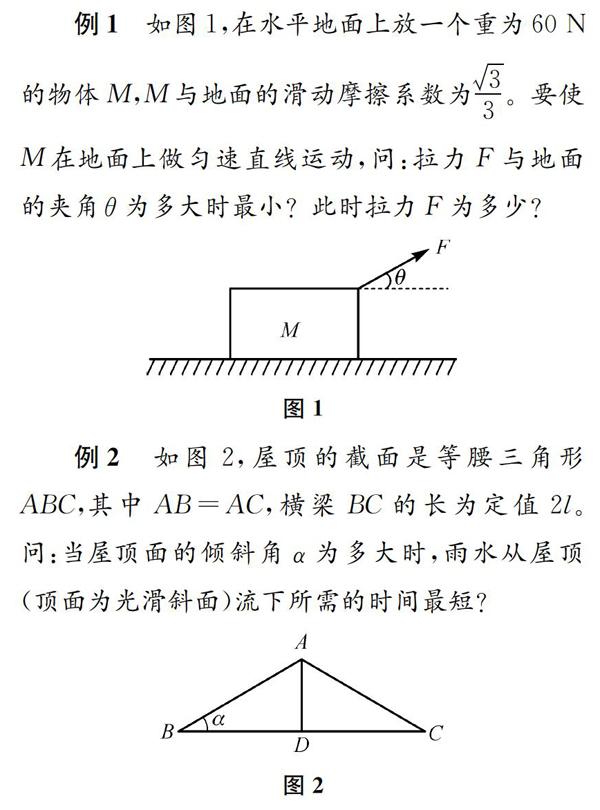
例1如图1，在水平地面上放一个重为60 N的物体M，M与地面的滑动摩擦系数为33。要使M在地面上做匀速直线运动，问：拉力F与地面的夹角θ为多大时最小？此时拉力F为多少？

图1

例2如图2，屋顶的截面是等腰三角形ABC，其中AB=AC，横梁BC的长为定值2l。问：当屋顶面的倾斜角α为多大时，雨水从屋顶（顶面为光滑斜面）流下所需的时间最短？

图2

这两道题出示后，学生感觉很惊讶：数学课上怎么出现了物理题？笔者说道：“牛顿在解决物理问题时发明了微积分，爱因斯坦等著名物理学家也都是顶尖数学高手。希望同学们今后也能成为这样的跨学科高手。”受此激励，学生探索的热情高涨。

对于例1，学生设地面对物体的弹力为N，物体与地面的滑动摩擦力为f，得f=μN后，通过物体的受力分析和正交分解法，得到Fcosθ-f=0，N+Fsinθ=G，从而解得F=μGμsinθ+cosθ=60sinθ+3cosθ=30sin （θ+60°），故当θ+60°=90°，即θ=30°时，拉力F最小，为30 N。

对于例2，学生将雨滴看成质点，利用受力分析和正交分解法，得到它沿AB下滑的加速度为gsinα，根据匀加速运动的位移公式，得到AB=s=12gt2sinα;根据等腰三角形的性质，得到AB=BDcosα=lcosα;因此，lcosα=12gt2sinα，即有t2=2lgsinαcosα=4lgsin2α，故当sin2α=1，即α=45°时，t取得最小值，此时雨水从屋顶流下所需的时间最短。

从两道题的解决过程中，我们可以发现：问题所涉及的知识都是数学与物理的主干知识，用到的数学和物理的思想、模型都是最常见、最重要的。例1综合了物理学中的受力分析和数学中的三角函数变换与最值以及方程思想，例2则综合了物理学中的受力分析、位移公式和数学中的等腰三角形性质、三角函数变换与最值以及方程思想。这两题让学生印象深刻，帮助学生积累了跨学科运用知识解决问题的经验，提升了跨学科素养。

（二）研究课程标准，寻求方法的结合点

课程标准给出了各个学科的主干知识和关键能力，除了涉及相关知识、技能层面的交叉、融合，还会展现思想方法和学习策略层面的渗透和相通。例如，数学建模与科学探究，其过程和方法极为相似。笔者通过与物理、信息技术教师协作，设计了《探究不同杯子的保温效果》一课，把“函数模型及其应用”“物体的冷却规律”和防水温度传感器有机结合起来，收到了较好的教学效果。简要教学过程如下：

教师提出问题：“生活中的杯子无论形状、大小还是材质不同，其保温效果都可能有差异。将65℃的热水分别倒入大小相同的圆柱形无盖陶瓷杯和玻璃杯，哪个保温效果更好？”学生猜测陶瓷杯的保温效果更好，主要依据是物理学中有这样的结论：陶瓷的导热性比玻璃差。

“这一猜测是否成立呢？”教师利用Romeo控制器、USB数据线、两个防水温度传感器、秒表等实验器材，每隔5分钟，分别测量两只杯子中的水温，等串口监视器上的温度基本稳定后记录数据。测量5次后停止，數据记录如表1所示。学生从表中发现，玻璃杯中水温比陶瓷杯中水温下降得略快一些，但每次测量值的差异并不大，仅在0.02℃至0.26℃之间，考虑到测量误差等因素，这样的差异可以忽略不计。

“为什么与我们先前的假设不相符呢？如果改变杯子的材质、壁厚、容量，测得的数据又会如何？”学生在后续的分组实验中发现，不盖盖子时，保温效果的差异不大;盖上盖子后，保温效果的差异较大。

在评价与反思阶段，学生终于道出了原因：在变量的控制过程中，有无盖子决定了保温效果，即导热性必须在封闭容器中才能得以体现，而在无盖状态下，杯子主要依靠杯口向外散热。

然后，教师引导学生通过查阅发现，物体在常温下的温度变化可以用牛顿冷却规律来描述：设物体的初始温度是T0，经过一定时间t后的温度是T，则T-Ta=（T0-Ta）12th，其中Ta表示环境温度，h称为半衰期。又让学生将表1中测得的初始、5分钟和10分钟时的温度代入，计算得到环境温度约为24℃，发现其与室温基本吻合。

回顾上述教学过程，首先，从问题引入，引出了实验操作的必要性，激发了学生探究的心向;其次，运用信息技术获得了相应的数据，但结果又出乎学生的预料，从而点燃了学生进一步探索的热情;再次，通过回顾反思、执果索因、关联变量，重新对数据加以分析、综合和评价，发展了学生的理性思维和批判性思维，培养了学生的科学精神和探究能力;最后，回归数学教材上提出的物理模型，通过数据的拟合、函数与方程思想的应用，加以定量分析。这样，从实验操作到数据统计，从定性分析到定量计算，从物理规律的理解到数学模型的建立，始终围绕科学探究的主线，从而使跨学科教学自然、有序、和谐地开展。

（三）发掘真实问题，拓展应用的边界

在数学教学中进行跨学科整合，关键是要找到真实的问题。这些问题一方面要指向数学教学目标，对学生的数学知识、技能、思想方法和思维策略等具有丰富的教学价值;另一方面要具备启发性、探索性、应用性、综合性和拓展性等特征，对学生的理解力、思考力和创新力等核心学力有较好的训练和滋养价值。要设计出这样的问题链，学校应组建相应的跨学科教师团队，通过分工、协作和研讨，发掘社会实践、生产生活中可利用的资源，整合各个学科的课程目标，把跨学科的学术形态转化为可实施的教学样态。

例如，苏教版高中数学教材在“圆的方程”与“抛物线的标准方程”中，都有一些与拱桥有关的例题或习题。笔者就以此引发学生讨论：究竟怎样的拱桥适合用圆来拟合数据？怎样的拱桥用抛物线来建立模型较好？由此引申出研究性学习课题：以无锡的桥梁变迁为例，谈桥的发展、建造和价值。这样的课题源于数学，又与人文、历史、物理、建筑、美学等学科相融合，可有效促进学生跨学科思维的形成和发展。

再如，教学“三角函数的图像与性质”时，可以联系物理中的圆周运动、简谐振动、波等知识，寻找真实的问题，如汽车发动机曲柄连杆的运动、潮汐现象等。

（四）回顾发展历史，获得成功的经验

从数学和科学的发展史来看，许多重大发现都离不开跨学科研究。因此，在课堂教学中，结合课程内容深入浅出地介绍这些历史，不仅能激发学生的兴趣，而且能让学生体验原创思维的价值，培养学生的创新意识和实践能力。另外，还可以结合科研的前沿动态，介绍社会生产中成功运用多学科知识解决具体问题的实例和方法，帮助学生养成跨学科思维的习惯。

比如，牛顿在研究物理学中的变加速运动、变力做功等问题时，采用微元分析的思想来解决，使数学的发展进入了微积分时代。在此过程中，无穷小量引发了一次数学危机。而莱布尼茨通过极限思想完善了微积分理论，不仅推动了数学的发展，而且促进了数学与物理的融合。其中，一些典型问题的解决，可以让学生领略到跨学科学习的魅力。

例如，在推导球的表面积公式时，因为球面剪开后不能铺平，所以笔者引导学生与刘徽的“割圆术”进行类比，即将球看成无数个顶点在球心、底面在球面上的“小锥体”，只要这些“小锥体”的底面足够小，就能把它们近似地看成高为球半径R的棱锥，而它们的底面积之和就等于球的表面积S，体积之和就等于球的体积V，于是有13SR=V=43πR3，可以得S=4πR2。这里的微元分析思想为学生后续的微积分学习做了孕伏。为了强化这一思想，笔者设计了这样一道物理题：

例3质量为m的物体以匀速率v沿半径为r的竖直圆形轨道运动。若物体与竖直圆形轨道间的摩擦系数为μ，问：物体从轨道最低点运动到最高点的过程中，摩擦力做了多少功？

这里，物体从轨道最低点运动到最高点的过程中，由于位置差异导致与圆形轨道之间的正压力不同，因此摩擦力也是变力。对此，只能利用微元分析思想，即把物体的运动无限细分，在每一个位移微元内，因为力的变化很小，所以可以看成在恒力作用下运动，然后将所有位移微元内的功相加，就得到总的功。具体解答如下：

解：如图3，由圆轨道的对称性，可在其水平直径上、下对称位置各取一点A、B，设OA、OB与水平直径的夹角为θ。在Δs=rΔθ的无限短圆弧上，Δs可以看成线段，物体受到的摩擦力可以看成恒力。故在A、B两点附近的Δs内，物体受到的摩擦力所做的功为ΔW=-μN1rΔθ-μN2rΔθ。

由题意，物体在A、B两点以速率v做圆周运动，故N1-mgsinθ=mv2r，N2+mgsinθ=mv2r。两式相加，得N1+N2=2mv2r，故ΔW =-2μmv2Δθ，故当θ从0取到π2时，摩擦力对物体所做的总功为-2μmv2π2，即-πμmv2。

本题不仅综合了圆的切线性质、弧度制、弧长公式及重力、弹力、摩擦力、向心力、圆周运动、功等数学和物理学主干知识，而且必须在对称、转化以及微元分析等核心思想方法的引領下，才能获得解决问题的思路，从而体现了数学、物理单学科核心素养向跨学科核心素养的转变。

最后，需要指出的是，由于以数学为中心的高中跨学科教学研究尚处于起步阶段，相关课程资源匮乏，因此，需要数学教师通过学习和探索，并与其他学科教师进行沟通和协作，有效开发内隐的课程资源，设计出既与高中数学课程相匹配，又与其他学科相融合，最好是符合社会生产、生活实际的问题，作为中心题目和学习任务，并在国家、地方、学校三级课程的实施、评价过程中，不断优化、改进与完善，从而为培养德才兼备的复合型、创新型人才提供良好的范例。本文中所举的案例主要体现的是数学与自然科学、信息技术等学科的整合，而与社会科学、人文科学等学科的整合（比如与古典诗词的融合）将是笔者进一步研究的重要方向。

本文系江苏省教育科学“十三五”规划2020年度重点资助课题“以高中数学为主导的跨学科教学研究”（编号：Ba/2020/02/47）的阶段性研究成果。

参考文献：

[1] 李佩宁.什么是真正的跨学科整合——从几个案例说起[J].人民教育，2017（11）.

[2] 陈静.新课改下数学教学中的跨学科意识[J].数学教学研究，2007（7）.

[3] 梅浩，袁智强，郑柯.基于数学实验的STEM教育——以“探究金属的冷却模型”为例[M].教育研究与评论（中学教育教学），2019（3）.

[4] 任念兵.从“数学欣赏”教学谈课程整合[J].教育研究与评论（中学教育教学），2018（1）.