高中数学解题中分类讨论思想的使用

李亚男

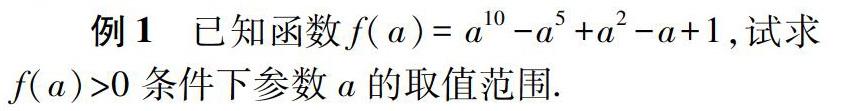
分类讨论是一种非常经典的数学思想，这种思维方式可以在解决各种实际问题中应用，在问题解析上发挥的效果非常明显.教师要在解题教学时让学生熟悉这种思维方法，并且要培养学生在解答相对复杂问题时形成良好的分类讨论意识.这可以很好地避免漏解的问题，能够让问题解答更加完整而准确.教师可以首先结合平时讲解的各类例题让学生感受分类讨论思想的使用，在学生头脑中建立基本认知;随后，可以让学生在各种习题练习中尝试这种思维方法，加强学生的分类讨论意识.这会让学生的解题能力得到很好的强化，也是提升学生综合学科能力的训练方式.

一、函数问题中分类讨论思想的使用

函数问题是高考数学中最常出现的考点，很多函数问题不仅会考查学生对基础知识的吸收掌握程度、思维的灵活性和完整性，也需要学生掌握一些有效的解题方法和技巧，善于利用函数性质来将问题有效解答.在一些相对开放的函数问题的分析讲解中，教师要让学生在解答时思维保持严谨.如果题设条件并不是太充分，要让学生看到各种可能性，在不确定的情况下可以以分类讨论作为切入点，结合各种可能性分别进行计算，再将各种可能的答案归纳汇总.

例1 已知函数f（a）=a10-a5+a2-a+1，试求f（a）>0条件下参数a的取值范围.

分析：函数f（a）本身涉及多个多项式，它们的底数相同，而指数函数本身具有很强的单调性特性，且单调性情况与底数值的大小情况具有紧密联系.这样的背景下，很有必要让学生将底数a可能存在的情况展开分类讨论.教师可以指导学生选取几个划分区域，从几个不同层次展开分类讨论，分别为：（1）a<0;（2）a=0或a=1;（3）01.以这样的方式来逐一解答，这能够让解析过程更加完整，能够避免漏解的发生.

二、概率问题中分类讨论思想的使用

概率问题同样是高中数学中很有代表性的考题类型，很多时候学生之所以会在概率问题中失分，很重要的原因在于没有将各种情况考虑在内，这说明学生的思维不够严谨，解题素养还有待进一步提升.在遇到有的概率问题时，学生会感觉找不到切入点，不知道如何解答，好像题目的条件给定不够完整.这种背景下教师应当让学生从题设出发，展开相应的分类讨论过程.

例2 在某个国家举办奥运会的时候，该国举办了火炬传递活动，其中18位火炬传递手的编号依次为1，2，3……18，试求从其中任选3人后能够构成以公差为3的等差数列的概率.

分析：首先教师要让学生明确，这是一道典型的古典概型问题，总数C=17×16×3.为了准确确定最后能够构成满足等差数列的各种结果，避免出现遗漏某一种情况，教师可以引导学生展开相应的分类讨论.可以先假定构成的等差数列为bn=b1+3（n-1），随后可以分别就b1=1，2，3的三种情况展开讨论，最后将结果汇总即可.这个问题的解析中首先需要学生构建一个数列，随后利用分类讨论思想对各种可能性展开分析总结.学生如果以这样的思路解答问题，不仅解题过程清晰明确，也不会产生漏解的状况，是一种很值得推崇的教学过程.

三、数列问题中分类讨论思想的使用

在遇到一些相对复杂的数列问题时，教师同样要引导学生形成分类讨论的思维.有些数列问題的看上去非常复杂，让学生觉得不知道如何下手.面对这样的问题，教师要让学生梳理自己的思维，提炼题设中的关键信息，形成基本的解题思路.如果面对的是一个综合性问题，如一个大题中有几个小问，且问题之间有一定关联，这时需要提醒学生注重问题的关联性，往往上面问题的解答是下面问题解答的铺垫.在面对后面的比较复杂的问题时，教师同样可以指导学生采取分类讨论的思想.

例3 已知等比数列{bn}，其中b1=1，前n项和为Sn，且bk+1，bk+2，bk+3构成等差数列（k∈N），试求：（1）试求数列{bn}的公比q;（2）Sk+1，Sk+2，Sk+3是否构成等差数列？（k∈N），为什么？

分析：这个问题有两个小问，教师首先要让学生求出公比q，这个可以利用函数概念加以求解，得出来的结果为q=1或q=-12.有了这个结果后随之便可以引导学生展开分类讨论，可以让学生分别讨论当q=1及q=-12时给出的数列能否构成等差数列，并说明原因，将问题有效解答.这种有一定综合性的问题看上去复杂，但是，只要教师引导学生理清思维，让学生循序渐进地进入到解题思路中，问题会变得越来越简单直观，解答的效果也会十分理想.