艉部新型球面舱壁结构强度及稳定性分析

侯磊

海军装备部驻武汉地区第二军事代表室，湖北 武汉 430064

0 引 言

艉端耐压球面舱壁是潜艇特种结构型式之一。球面舱壁结构一般由球壳、过渡环壳和耐压柱（锥）体组成[1]。针对球面舱壁的结构型式、强度和稳定性等，前人已开展大量研究。熊景毅等[2]利用适用于球面舱壁结构强度计算的Riccati传递矩阵法，讨论了球壳半径、过渡环半径、边界刚度等对球—环—柱球面舱壁结构强度的影响，同时提出了扁平度概念，并给出了其建议取值范围。胡国栋[3]分析了端部球面舱壁为半球壳时各结构的几何尺寸关系，得到了过渡短环壳半径关于锥角、锥壳长度和球面壳半径的计算公式，计算了球面舱壁稳定性，分析了这3部分结构参数对舱壁的影响，并基于等强度分析上述结构的厚度变化趋势，验证了其正确性。李荣富等[4]提出了鞍形舱壁结构，并与等重量的传统三心球面舱壁结构进行了对比，得出鞍形舱壁结构比等重量的三心球面舱壁结构动力屈曲载荷有明显提高、且对初始缺陷不敏感的结论。黄旎等[5]采用Riccati传递矩阵法对均匀外压下球面舱壁的弹性稳定性问题进行了数值模拟，并得出在球壳半径、球壳厚度、环壳半径、环壳厚度和锥壳半锥角等参数中，仅球壳半径和球壳厚度对结构的临界压力和失稳波数起决定性作用。Menaa等[6]采用混合有限元方法研究了充液球壳的自由振动问题，得到了不同填充比下的振动频率，并与实验结果进行对比，总结得到了不同壳体几何形状、填充比和不同半径与厚度比边界条件下的动力特性。

针对耐压球面舱壁上开口应力集中和加强方式的问题，Jullien等[7]对受轴向压力的开孔薄柱壳进行研究，得到了形状壳屈曲特性与孔半径除以壳半径和厚度乘积的平方根有关的结论。余俊等[8]基于回转壳的基本微分方程组，建立了一种受静水压力作用下小开孔球壳强度分析的解析单元法（AEM），解决了传统回转壳方法计算小开孔应力误差较大的问题。许汀[9]针对鞍形舱壁结构的壳体与加强环连接处的应力集中问题，分析了应力系数的变化趋势和影响范围，考虑了球壳中心开轴孔对舱壁强度的影响，可为鞍形舱壁设计提供参考。俞铭华等[10]利用ANSYS软件对开有人孔、观察窗的耐压球壳进行了非线性分析，计算了局部缺陷范围及幅值的变化对壳体极限强度的影响，结果表明，有围壁加强的开孔耐压球壳与无开孔耐压球壳的极限强度相差不大。张航[11]采用ANSYS软件对侧壁加强、垫板加强、肘板加强3种形式的结构极限强度进行了对比分析，得到肘板加强具有更高的极限强度的结论，并提出了梯形加强的开孔加强形式。

传统艉部球面舱壁直接在球壳上开艉轴孔，为了使艉部具有更大的布置空间，有利于优化轴系布置，并减小艉部振动，本文将提出一种艉部新型球面舱壁结构，即在原球壳上增设一个小球面舱壁，并对其强度和稳定性进行分析，探讨结构参数对新型球面舱壁结构强度和稳定性的影响，用以为球面舱壁结构工程设计提供参考。

1 计算模型和载荷施加

新型球面舱壁结构型式如图1所示，其在原来的球面舱壁上增设一个小的球面舱壁，使艉部具有更大布置空间；大球面舱壁与小球面舱壁采用围栏的方式进行连接，具体结构尺寸如表1所示。本文采用SOLID185单元建立其有限元模型，图中：Y轴是轴向，X轴是径向，Z轴是周向。

图 1 新型球面舱壁结构示意图Fig. 1 Schematic diagram of new spherical bulkhead

表 1 新型球面舱壁结构尺寸Table 1 Structure sizes of the new spherical bulkhead

模型材料的弹性模量为196 GPa，泊松比为0.3，屈服强度为590 MPa。计算极限承载能力时，采用理想弹塑性材料模型，缺陷形式为第1阶失稳波形，幅值为球面舱壁厚度的0.2倍。网格尺寸在大、小球面舱壁处设置为5等份，其余为20 mm。经计算，该网格能保证计算结果的收敛性。图2为大、小球面舱壁与围栏的网格划分情况。

图 2 大、小球面舱壁与围栏的网格划分Fig. 2 Mesh division of big and small spherical bulkhead and fence

在结构外表面施加4 MPa的静水压力，在靠近锥壳一端约束X，Y，Z方向的平动自由度，并将端面水压转化为节点力，沿轴向施加在艉端节点上。模型的约束情况和载荷示意图如图3所示。

图 3 计算模型约束和载荷示意图Fig. 3 Constraints of computational model and schematic diagram of load

2 新型和传统球面舱壁结构的强度和稳定性分析

当大球面舱壁厚度为28 mm，围栏厚度为20 mm时，比较新型和传统球面舱壁结构的强度和稳定性，Mises应力云图如图4所示，可见新型球面舱壁结构最大Mises应力出现在围栏附近，传统球面舱壁结构最大Mises应力出现在过渡环壳处。第1阶失稳波形如图5所示，可见新型球面舱壁在靠近围栏位置出现失稳现象，而传统球面舱壁在大球面舱壁上出现失稳现象。

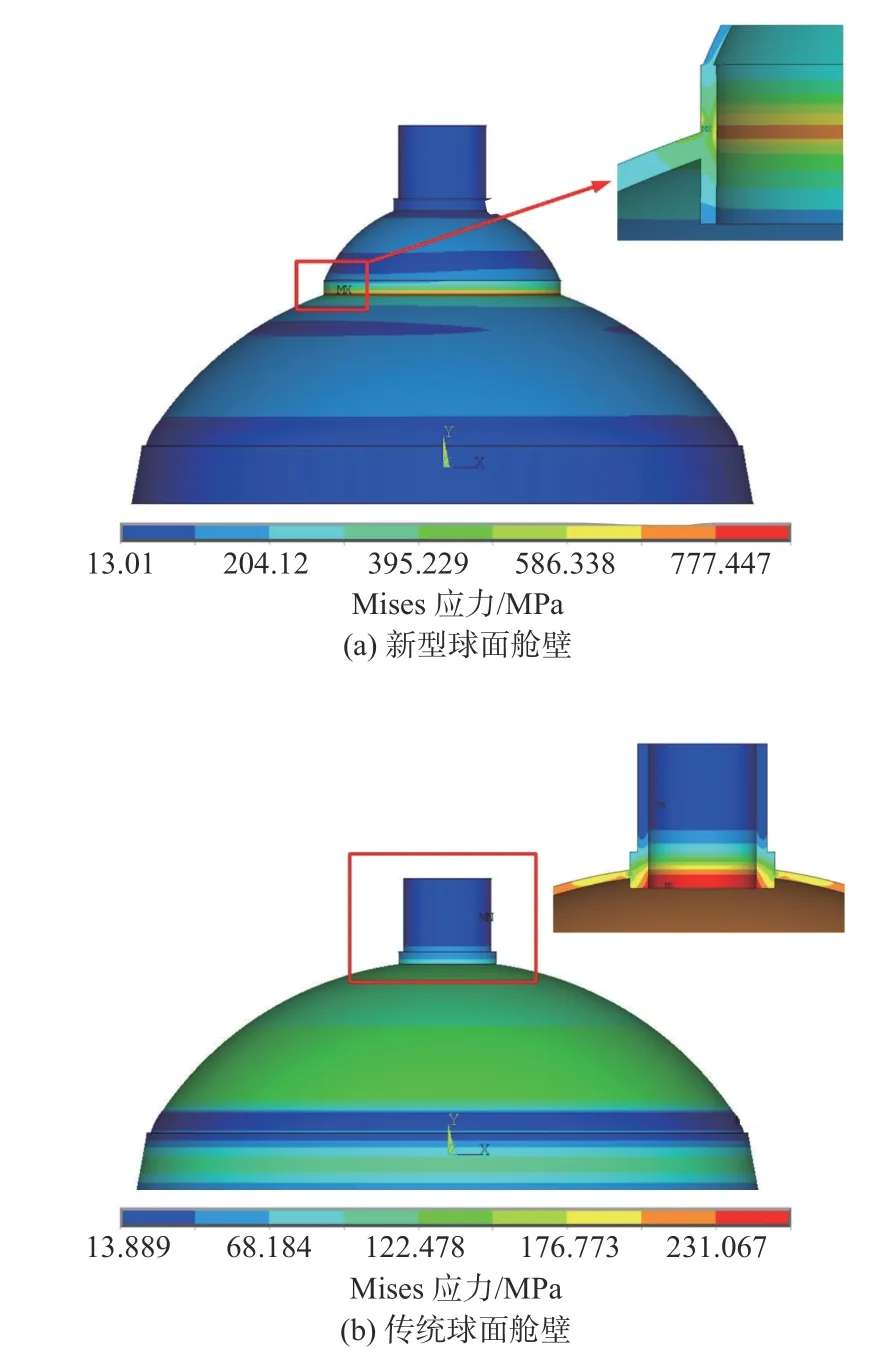
图 4 球面舱壁的Mises应力云图Fig. 4 Von Mises stress contours of spherical bulkhead

计算结果如表2所示。由图4、图5和表2可知，相对于传统球面舱壁，新型球面舱壁的最大Mises应力出现在围栏附近，且增加了238.1%；第1阶失稳特征值降低了50.1%；极限承载能力降低了51.4%。为了降低新型球面舱壁结构的最大Mises应力，提高稳定性和承载能力，需要增加围栏厚度。

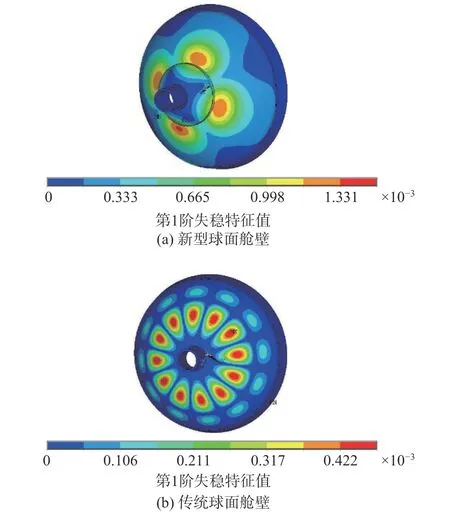
图 5 第1阶失稳波形示意图Fig. 5 Diagram of the first-order instable waveform

表 2 计算结果对比Table 2 Comparison of calculation results

3 围栏厚度对结构强度和稳定性的影响

基于上述模型，围栏厚度分别取值为20，40，60，80，100 mm时，计算各方案的强度和稳定性，得到Mises应力云图如图6所示，第1阶失稳波形如图7所示。

由图6可以看出，当围栏厚度为20和40 mm时，最大应力出现在围栏附近；当围栏厚度为60，80和100 mm时，最大应力出现在球面舱壁过渡环壳处。

由图7可以看出，5种方案均在靠近围栏位置出现第1阶失稳现象。5种方案的结构强度、稳定性和极限承载能力的计算结果如表3所示。

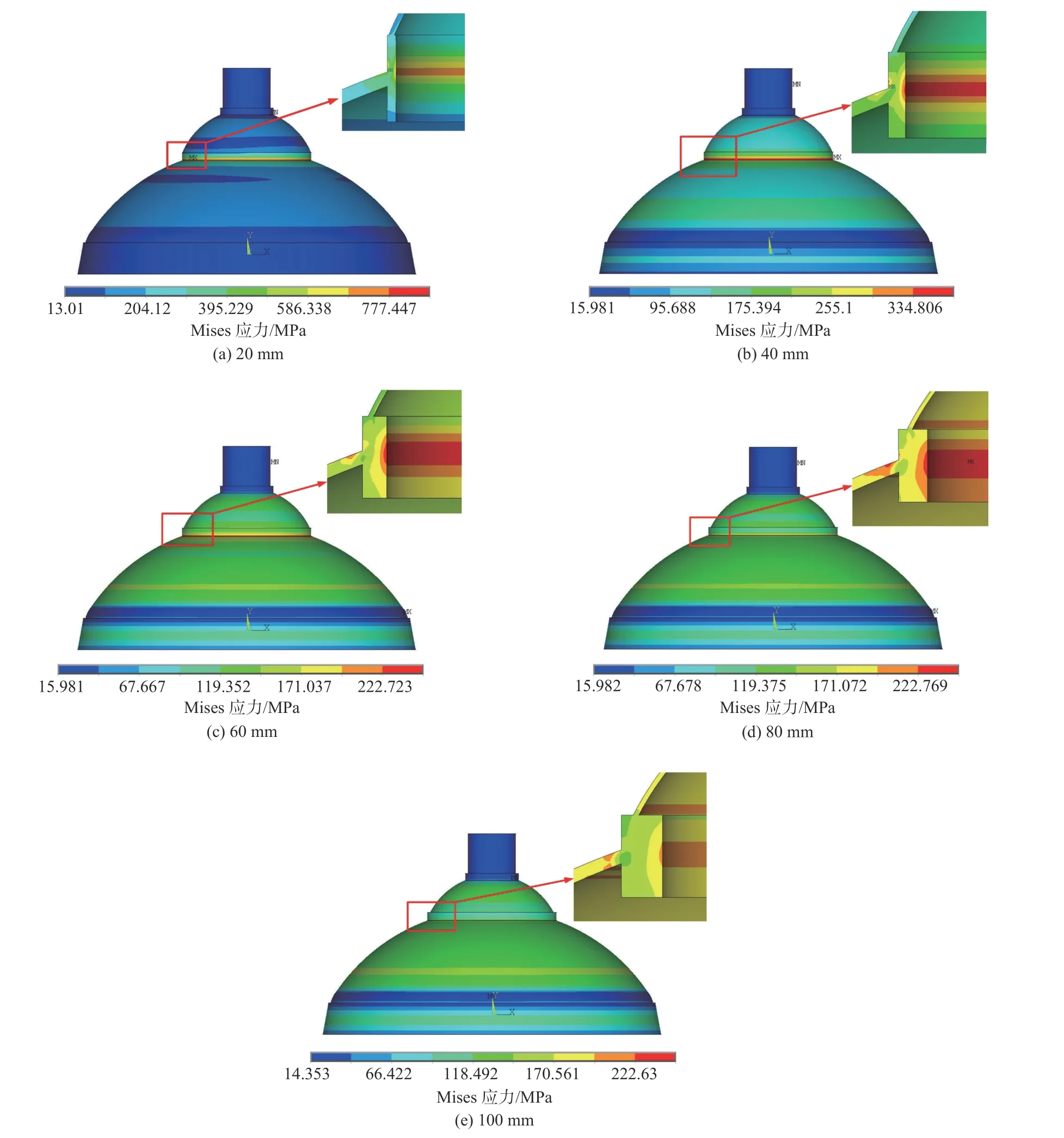
图 6 舱壁围栏厚度不同时的Mises应力云图Fig. 6 Von Mises stress contours of bulkhead with different thickness fence

根据计算结果绘制的曲线如图8所示。由表3和图8可知：随着围栏厚度的增加，第1阶失稳特征值呈现近似线性增长趋势，极限承载能力也逐步增加。当围栏厚度从20 mm增加到100 mm时，第1阶失稳特征值和极限承载能力分别增加了96.1%和129.6%；针对结构强度，当围栏厚度为20和40 mm时，最大Mises应力出现在围栏附近，增加围栏厚度可以快速减小应力；当围栏厚度从20 mm增加到40 mm时，最大Mises应力减少了57.1%；当围栏厚度为60，80和100 mm时，最大Mises应力出现在球面舱壁过渡环壳处，增加围栏厚度对过渡环壳处的应力无影响，而围栏附近的应力相对于20 mm围栏厚度时分别减少了73.5%，80.0%和80.8%，这说明继续增加围栏厚度对围栏附近应力的改善效果减小。

当大球面舱壁厚度为28 mm，围栏厚度100 mm时，新型球面舱壁结构和传统结构的强度和稳定性水平基本一致；当围栏厚度为60或80 mm时，新型球面舱壁结构和传统结构的强度水平基本一致。

4 不同球面舱壁厚度下围栏厚度对结构强度和稳定性的影响

当大球面舱壁厚度分别为24和26 mm时，研究围栏厚度对结构强度和稳定性的影响。数值计算结果分别如表4和表5所示。图9为大球面舱壁厚度24 mm，围栏厚度100 mm时的第1阶失稳波形。由图9可见，失稳位置在大球面舱壁上，此时决定第1阶失稳特征值的是大球面舱壁厚度。其他工况条件下的失稳位置均在围栏附近。

图 7 围栏厚度不同时第1阶失稳波形示意图Fig. 7 Schematic diagram of the first-order instable waveform with different thickness fence

表 3 大球面舱壁厚度为28 mm时计算结果对比Table 3 Comparison of calculation results with 28 mm thickness large spherical bulkhead

根据计算结果绘制的曲线如图10所示。由表4，表5和图10可知，在不同的球面舱壁厚度下，围栏厚度对结构强度和稳定性的影响规律为：随着围栏厚度的增加，第1阶失稳特征值呈近似线性增长趋势，极限承载能力也随之增加。当大球面舱壁厚度为24 mm，围栏厚度从80 mm增加到100 mm时，第1阶失稳特征值增幅较小，这与图9所示第1阶失稳波形相关，说明当围栏厚度增加到一定程度，其失稳波形出现在大球面舱壁上，球面舱壁厚度对结构稳定性的影响更大，而围栏只是作为其支撑结构，所以再增加围栏厚度对稳定性的提高效果不大。当围栏厚度由20增加到40或60 mm时，围栏处最大Mises应力快速减小；但是当围栏厚度超过60 mm后，继续增加围栏厚度对围栏附近Mises应力的改善效果不明显。

图 8 大球面舱壁厚度为28 mm时的计算结果Fig. 8 Calculation results with 28 mm thickness large spherical bulkhead

图 9 大球面舱壁厚度为24 mm，围栏厚度为100 mm时第1阶失稳波形Fig. 9 Diagram of first-order instable waveform with 24 mm thickness large spherical bulkhead and 100 mm thickness fence

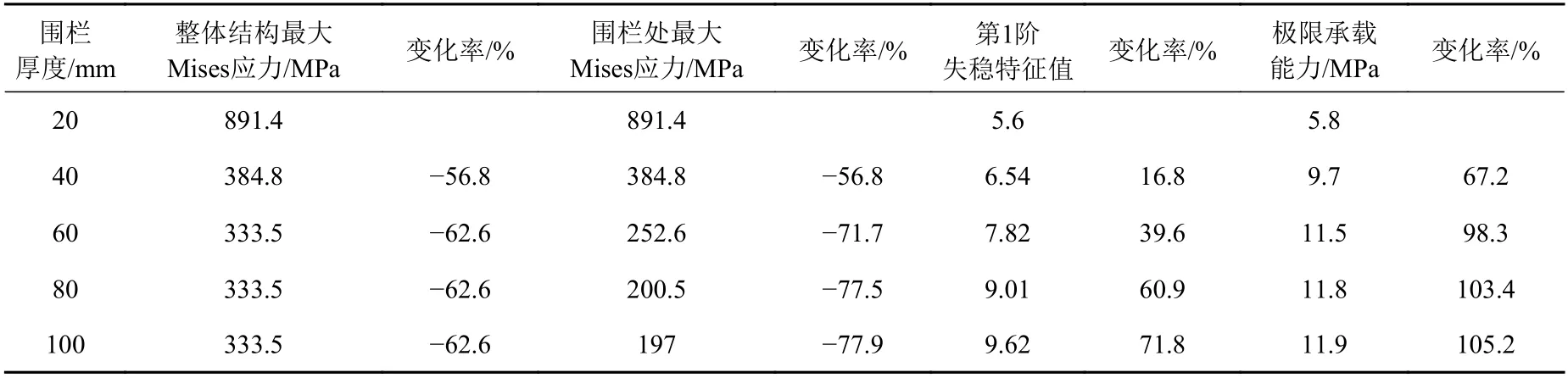
表 4 大球面舱壁厚度为24 mm时计算结果对比Table 4 Comparison of calculation results with 24 mm thickness of large spherical bulkhead

表 5 大球面舱壁厚度为26 mm时计算结果对比Table 5 Comparison of calculation results with 26 mm thickness of large spherical bulkhead

图 10 不同大球面舱壁厚度的计算结果汇总Fig. 10 Calculation results of large spherical bulkhead with different thicknesses

5 结 论

本文对艉部新型球面舱壁结构进行强度和稳定性分析，并探讨了结构参数对新型球面舱壁结构强度和稳定性的影响，得到如下结论：

1） 随着围栏厚度的增加，第1阶失稳特征值不断增加，呈近似线性增长趋势，当大球面舱壁厚度为28 mm，围栏厚度为100 mm时，新型球面舱壁的强度和稳定性达到传统舱壁的水平。

2） 当最大应力出现在围栏处时，增加围栏厚度可以很好地减小其应力；当围栏厚度增大到一定程度，最大应力转移到其他位置后，此时再增加围栏厚度对降低结构最大应力无益，且对围栏附近应力的改善程度也较小。

3） 仅当大球面舱壁厚度为24 mm，围栏厚度为100 mm时，由于第1阶失稳波形出现在大球面舱壁上，围栏厚度增加对舱壁结构稳定性的提高效果不明显。在其他工况下，针对不同厚度的大球面舱壁结构，增加围栏厚度时舱壁的结构强度和稳定性均增强，且变化规律基本相同。