计及流体影响的船舶回转冰阻力数值模拟

倪宝玉，黄其，陈绾绶，薛彦卓

哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

0 引 言

近年来，北极地区的航线开发和资源勘探问题受到了学者们的关注。随着极地冰的融化，极地航行难度降低，越来越多的船舶尝试在极地航行。在此背景下，研究极地航行船舶的操纵性就具有很强的现实意义。极地航行船舶除了需要承受风、波浪、水流等常规阻力外，还要承受冰阻力，在这些外部阻力中，冰阻力一般最为突出。当一艘船航行于层冰冰面时，船与冰的强烈非线性碰撞会对船舶的航行产生很大影响。因此，从保证船舶航行安全来说，能够准确预测船舶冰阻力至关重要。

自19世纪60年代起，针对于冰区航行船舶冰阻力及冰阻力影响下船舶运动的研究从未间断。Kim等[1]模拟了碎冰条件下货船的阻力性能，并将数值模拟结果与韩国水池的非冷冻模型冰试验结果以及加拿大冰池中的预锯冰试验结果进行了比较，取得了良好的一致性。Kajaste-Rudnitski和Kujala[2]采用商业软件ABAQUS对层冰条件下的船舶三自由度运动进行了模拟，结果显示破冰是一个随机的过程，冰阻力随时间的变化呈现出一系列持续时间非常短的尖峰波动。Valanto[3]通过理论计算和三维有限元模型预测了层冰条件下船舶受到的冰阻力，并进一步考虑了船体型线及水的影响。Su[4]开发了一种“点—面”接触算法用来计算船舶表面的冰阻力，并在此基础上通过自编程分析了船舶的阻力和机动性。Lau和Simões Ré[5]利用离散元法软件DECICE模拟了层冰和碎冰中破冰船的操纵性，并将其与模型试验结果进行比较验证了离散元模型的准确性。狄少丞等[6]基于离散元法模拟了破冰船在层冰和浮冰中的回转运动，冰与船之间的接触过程用球—三角接触模型表示，分析了冰厚度和冰密集度对冰阻力和回转直径的影响。

上述的数值模拟研究主要集中于船—冰强碰撞过程中的船舶冰阻力，没有考虑流体（海水）的作用，从而缺少流体对船舶冰阻力的影响研究。针对这一点，本文基于有限元分析中的流固耦合模型，模拟冰—水共同作用下船舶的回转运动。

1 数值模拟参数

本文采用ANSYS/LS-DYNA显式动力学分析软件，使用有限元法（FEM）模拟层冰中破冰船的回转运动。建立了船、层冰、空气域和海水域的三维模型，图1所示为隐藏了空气域后的数值模型示意图。

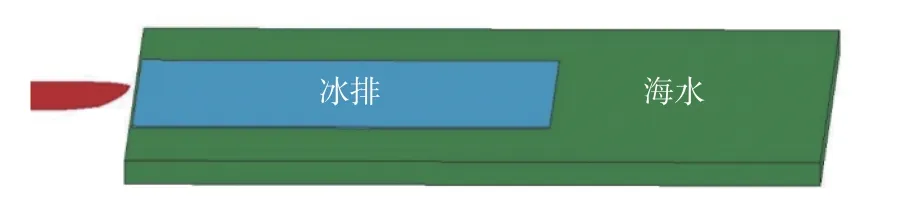
图 1 冰—水—船数值模型Fig. 1 Numerical model of ice, sea water and ship

模拟过程中，将船体视为刚体，船型的主要参数如表1所示。层冰的主要尺寸为600 m ×350 m × 1 m，冰网格采用1 m ×1 m ×1 m的六面体网格。已知冰层宽度（350 m）远大于船宽（22.6 m），边界对碰撞结果的影响已经很小，因此将冰的边界条件设定为非反射边界，从而模拟无限边界的情况。由于冰材料的复杂性和随机性，对于冰材料参数和模型的研究各有不同，目前较常用的一种做法是假设冰为各向同性弹塑性材料，如杨亮和马骏[7]以及Liu[8]的研究。为此，本文也选择此模型作为冰模型，相关参数的选取如表2所示，参数的选取及其合理性参见文献[7]。当单元的应力或应变超过有限元模型中的设定值时，该单元无效，将从模型中删除，不影响后续计算。

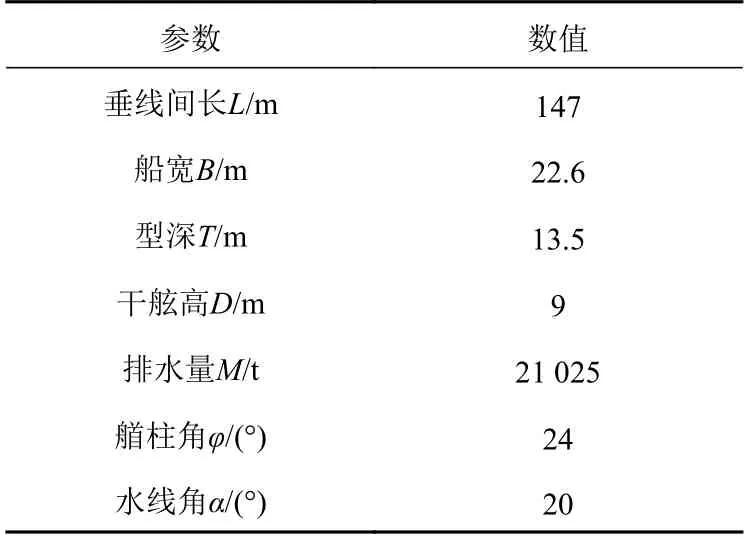
表 1 船舶参数Table 1 Ship parameters

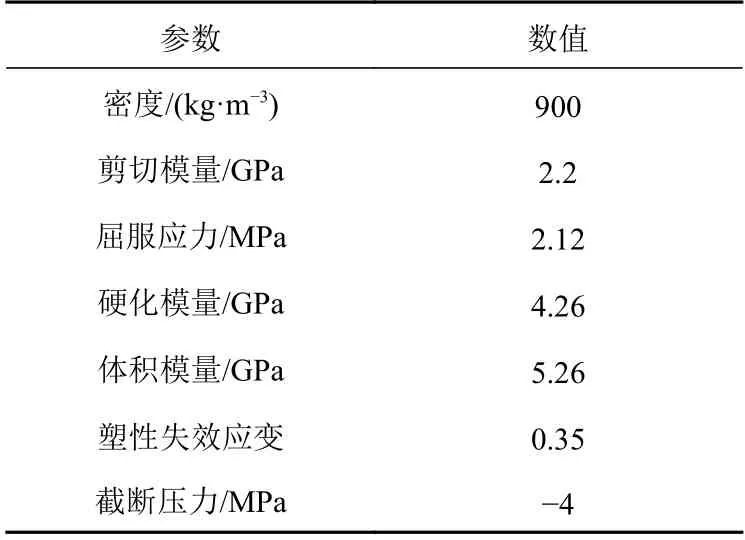
表 2 冰模型参数Table 2 Ice model parameters

空气域尺寸为800 m × 500 m ×10 m，海水域尺寸为800 m ×500 m ×15 m。流体域的网格在接触面连接，为保证流固耦合的精确度，采用等同于冰材料的1 m ×1 m ×1 m的六面体网格。对于流体的材料特性，采用软件中的“空材料”描述，并通过定义流体状态方程来描述压力和密度之间的关系。以海水为例，状态方程为Gruneisen状态方程[9]，是一种可压缩材料的状态方程，其公式为

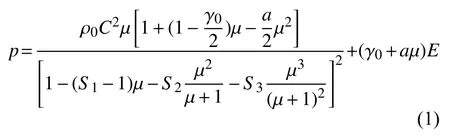
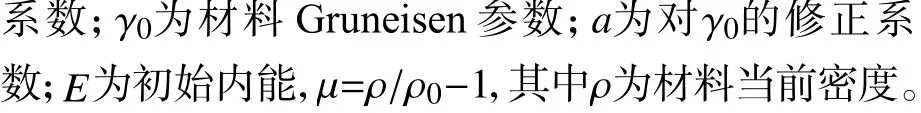
需指出的是，由于有限元软件中没有采用Naiver-Stokes方程求解流体运动，所以不能直接获得流体动力，不过通过该模型可以考虑冰在海水中的浮力。通过设定流体和固体的粘性与速度的耦合关系，将固体与流体耦合在一起。在考虑重力和动态阻尼的同时，设定海水域和空气域边界为无限边界，通过耦合固体和流域接触点的位移和形变，来防止流固分离。模型中的船体和层冰模型均与流体进行了相关的耦合。流固耦合方面的设置采用的是LS-DYNA软件中的Arbitrary Lagrange-Euler（ALE）算法，通过定义关键字的方法将流体和固体耦合在一起，流固耦合关键字选择“CONSTRAINED_LAGRANGE_IN_SOLID”。此后，设置流体与固体的耦合方式，LS-DYNA软件提供了多种耦合方式[10]，本文选用“罚函数耦合法”（penalty coupling），耦合的方向设定为接触节点的法向。此外，在流固耦合分析中还有很多必要的处理，如多物质单元的耦合方式等，鉴于篇幅限制，这里不一一介绍，具体可参见文献[10-11]。

在模型中，设定船舶的三自由度分别为纵荡、横摇和艏摇。初始时刻，随船坐标与全局坐标一致，其中随船坐标系的坐标原点为船舶重心，如图2(a)所示，随船坐标系的x轴指向船艏，y轴指向左舷，z轴指向上方。图2(b)所示为船舶艏部有限元模型的近视图。数值方法和建模的更多细节可以参考文献[12]。

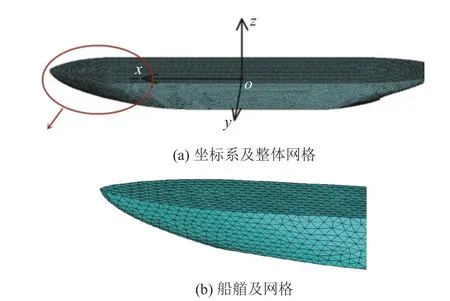
图 2 船舶坐标和有限元模型示意图Fig. 2 Sketch of coordinates and finite element model of the ship

2 网格收敛性分析及验证

2.1 网格收敛性分析

网格收敛性分析对于数值模拟具有重要意义。然而，由于船—冰—海水模型中存在大量网格的原因，很难减小网格尺寸。为了简化计算，选择了一个类似的冰—结构碰撞模型来检查网格的收敛性。

用这个简单的模型模拟了钢板挤压带有半球头冰柱的过程。在模型中，钢板设置为刚体，钢板和冰的材料参数及破坏模式与第1节相同。钢板的速度为1 m/s，冰柱底部固定。具体模型如图3所示。

图 3 平板—冰柱模型Fig. 3 Model of plate-ice cylinder

为了验证网格的收敛性，在不同冰模型网格尺寸下进行了数次模拟。设置了3种网格：100 mm×100 mm×100 mm，90 mm×90 mm×90 mm和80 mm×80 mm×80 mm。3种网格尺寸下的钢板冰阻力曲线如图4所示。由图可以看出，不同网格尺寸的冰阻力曲线随时间变化逐渐重合。此外，无论网格尺寸如何变化，冰阻力的剧烈振荡总是存在，这表明振荡来自平板和冰柱碰撞，而不是网格尺寸。

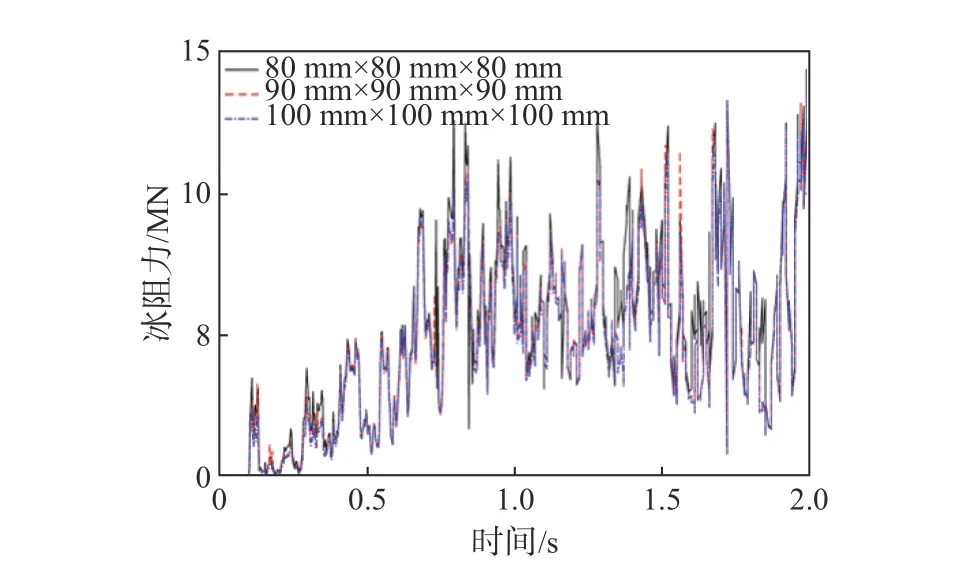
图 4 不同网格密度下的冰阻力Fig. 4 Ice resistance simulated by different mesh sizes

2.2 验证船与冰碰撞

在考虑流域影响之前，为了验证船和冰碰撞的数值模型，将数值模拟得到的船舶冰阻力与Lindqvist[13]经验公式计算出的冰阻力进行比较。保留与Lindqvist相同的部分输入，例如船速、冰厚、船型主要参数等。除此外，一些冰参数，如塑性硬化模量、体积模量和塑性破坏应变等在Lindqvist的方程中未使用，这些数据的选取需要根据先前的研究和经验值进行判断。在船和冰碰撞验证中，取船速 V=5 m/s，其他参数同上一节。Lindqvist的公式为

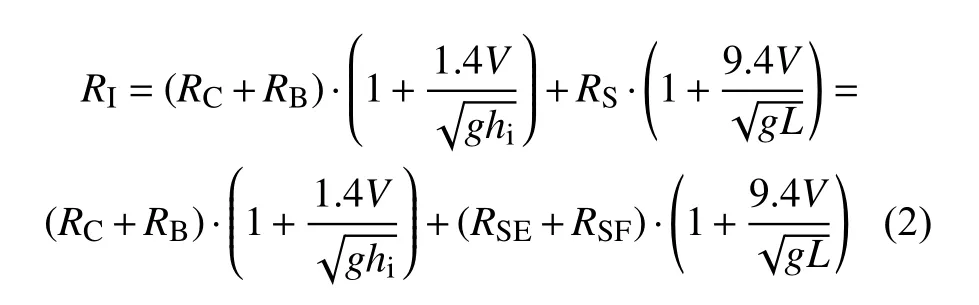
此时，冰的边界条件仍为无反射边界条件。数值模拟结果与经验公式的比较如图5所示。

由图5可以看出，数值模拟的平均值非常接近由经验公式计算的值。经验公式的结果为1.056 MN，数值模拟的平均值为1.055 MN，相对误差为0.1%。因此，可以认为数值模型的准确度在一定程度上得到了验证。

为进一步验证数值模拟的合理性，分别对1 m冰厚、不同航速，以及5 m/s航速、不同冰厚的情况进行了模拟，并将模拟结果与简化后的Lindqvist经验公式结果进行了对比，如图6所示，结果显示模拟结果基本合理。

2.3 验证流体与结构的相互作用

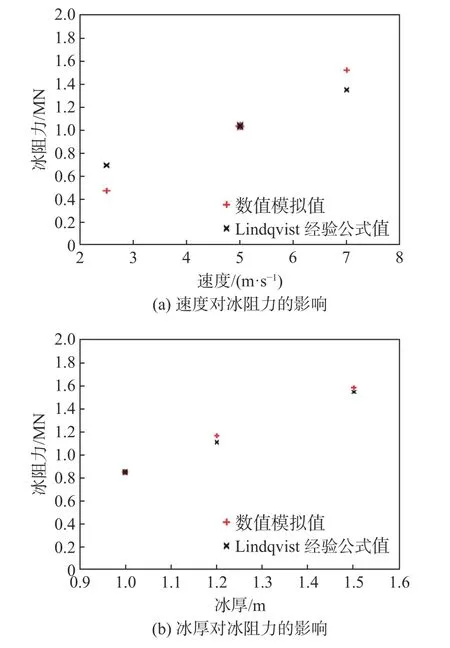
图 6 不同速度和冰厚条件下数值模拟结果和经验公式值对比 Fig. 6 Comparison of simulation results and empirical formulae under different speed and ice thickness conditions

在2.2节的基础上研究流体与结构的相互作用，在考虑流体存在的情况下，模拟层冰上的船舶冰阻力，并与经验公式计算值进行比较。所有参数与第2节相同。如式（2）所示，浸没阻力包括潜在能量损失和摩擦阻力损失。在层冰破碎后，碎冰沿着船舶滑动会引起摩擦阻力。在本文的模拟中，当冰模型单元的应力或应变超过有限元模型中的设定值时，冰模型单元将被判定为无效并从模型中删除，因而无法模拟碎冰沿船体滑动，也无法计算破冰后的摩擦阻力。因此，在本文的流体—结构相互作用模型中，只包含潜在能量损失。由此，方程（2）简化为

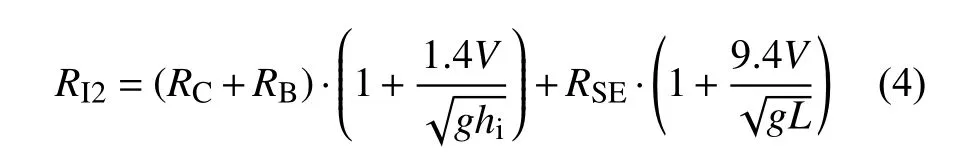
数值模拟结果与经验公式的比较如图7所示。经验公式的结果为1.481 MN，数值模拟的平均值为1.466 MN，相对误差为1%。因此，可以认为流体—结构相互作用方法在一定程度上得到了验证。比较图5和图7可以清楚地看到，冰阻增加了近28%，表明考虑海水对冰的支持作用后，增加了船舶的冰阻力。这说明海水的影响不可轻易忽视，应该在数值模拟中予以考虑。此外，对比图5和图7可知，当采用流固耦合方法进行分析时，冰阻力曲线的振荡程度降低了，表明海水缓冲了船与冰之间的碰撞，降低了冰阻力的随机性。

3 船与冰碰撞的数值模拟

3.1 不考虑流体域时的数值模拟

在数值模型验证的基础上，模拟船体在层冰条件下的水平回转运动。对于回转运动的模拟，假设船在以恒定角速度转弯之前以恒定速度直线前进。这里需要指出的是，由于操纵性涉及螺旋桨和舵力等复杂的推进力，本文并没有直接解决操纵性问题。但强制转弯运动期间的模拟结果对于船舶操纵性仍然具有参考意义，因为它们具有类似的破冰模式。全局坐标系中的速度可表示为：

图9所示为全局坐标系中，流固耦合作用下冰阻力随时间的变化。从图中可以看出，冰阻力呈现出一系列持续时间非常短的高峰，Kajaste-Rudnitski等[2]在冰船碰撞模拟中也观察到了这一点，且在回转运动中，冰阻力振荡的振幅比在直线运动中更大。

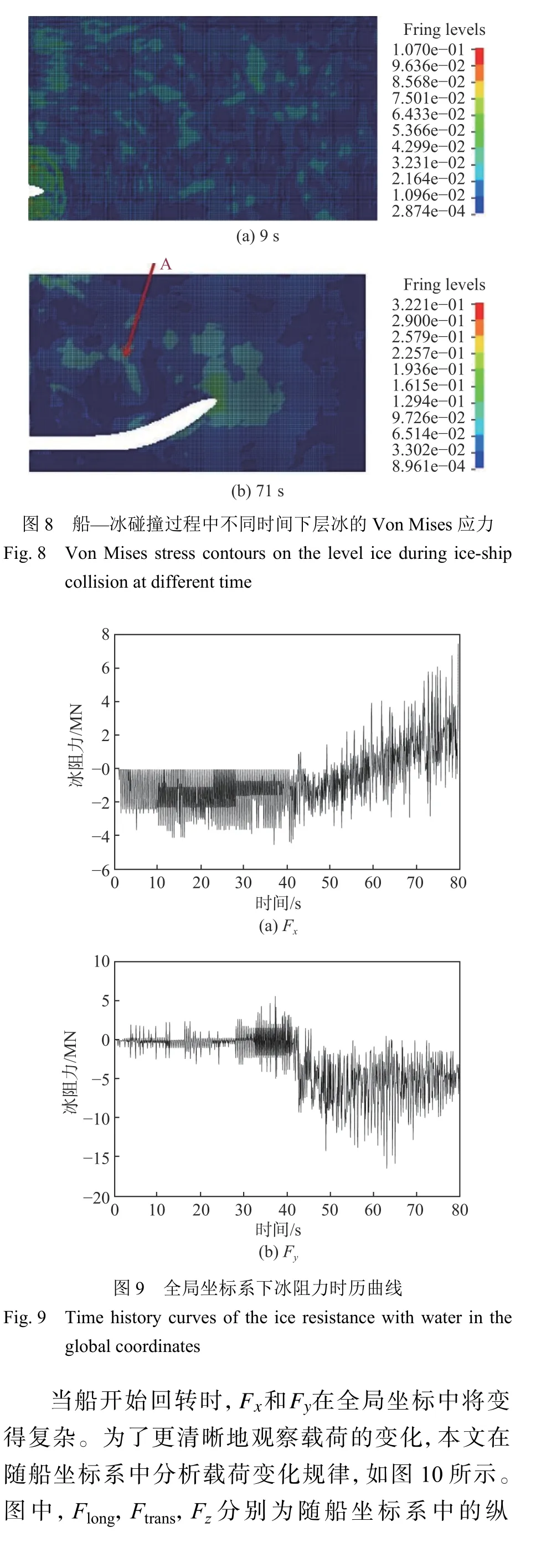
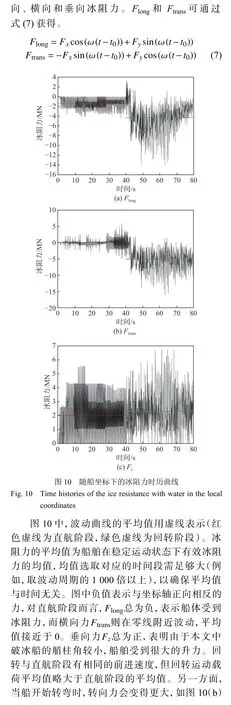
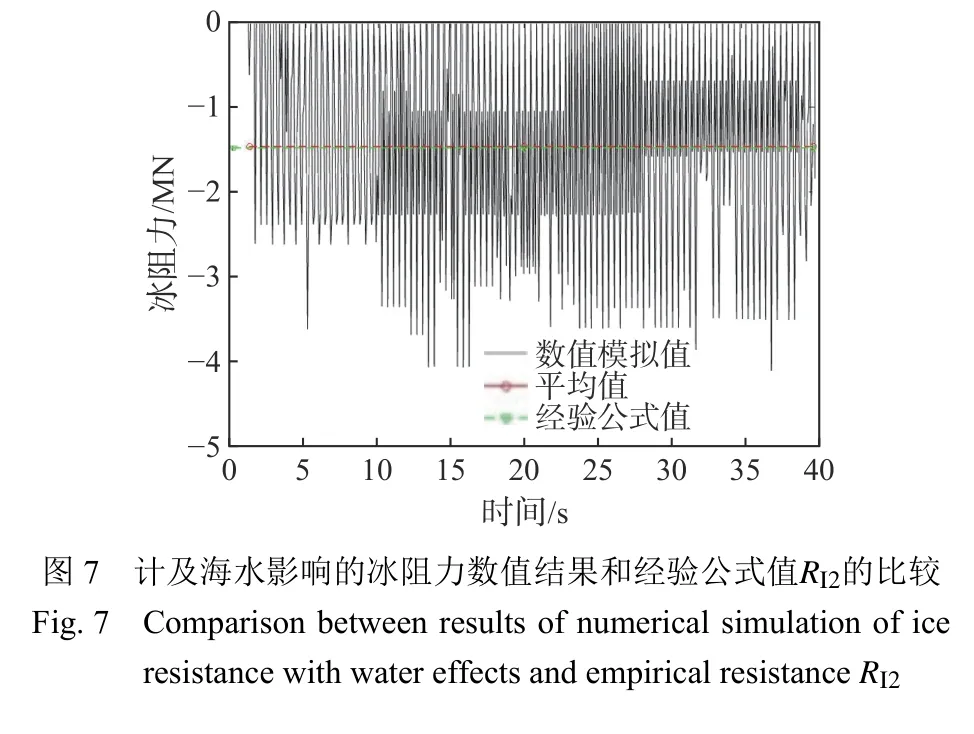
所示。右舷的冰阻力是由船左转时船体和冰航道内部之间挤压所产生。类似的现象也曾在其他学者基于离散元法[14]的研究中出现过。

3.2 考虑流体域时的数值模拟

为了研究海水域对冰阻力的影响，比较无流固耦合船—冰碰撞模拟和流固耦合船—冰碰撞模拟的冰阻力情况。

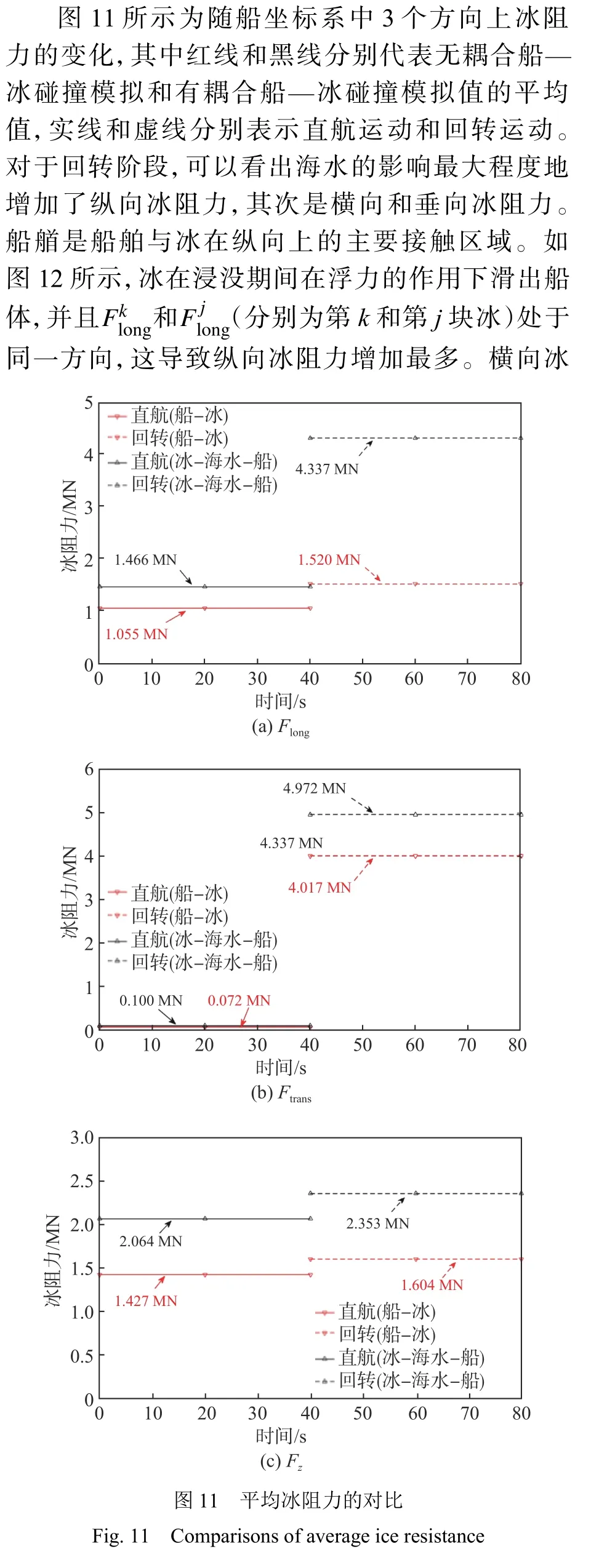
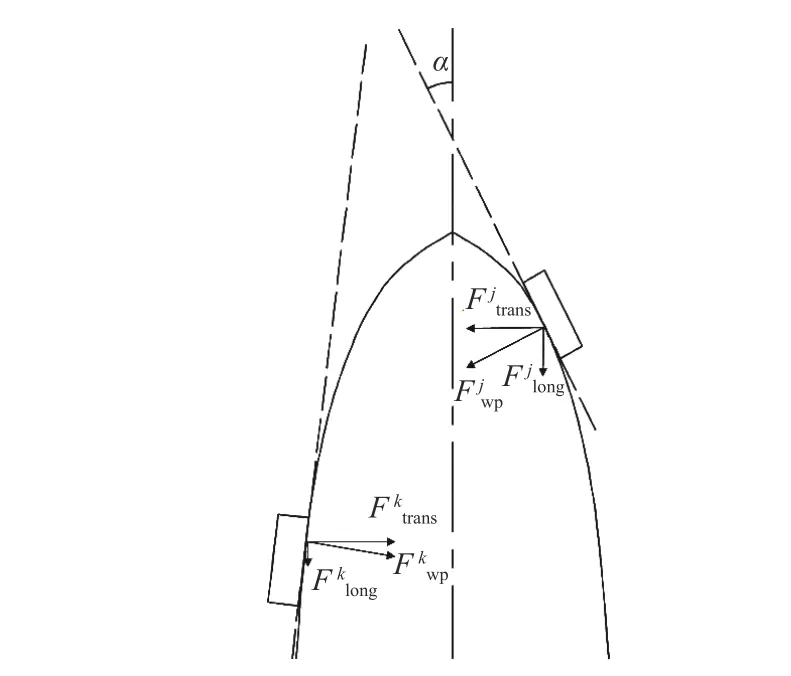
图 12 设计水线平面上冰阻力示意图Fig. 12 Sketch of ice resistance on the designed waterline plane

4 结 论

本文基于非线性有限元法和流固耦合模型，模拟层冰中船舶的回转运动，以研究水对冰阻力的影响，主要得出以下结论：

1） 海水的存在增加了船体在直线运动和回转运动中各个方向上的冰阻力，但每个方向的增量都不同。

2） 回转运动阶段，在海水的作用下，受海水影响最大的是纵向冰阻力，其次是横向和垂向冰阻力。

3） 当采用流固耦合方法进行分析时，冰阻力曲线的振荡程度降低，表明海水缓冲了船与冰之间的碰撞，降低了冰阻力的随机性。