基于改进梯度提升决策树—蒙特卡罗法的超大型集装箱船绑扎桥可靠性分析
2020-05-28李放王德禹
李放,王德禹*
1 上海交通大学 海洋工程国家重点实验室,上海 200240
2 高新船舶与深海开发装备协同创新中心,上海 200240
0 引 言
与大型集装箱船相比,超大型集装箱船的绑扎桥结构更高、更宽,且绑扎点分布于绑扎桥的不同高度平面,从而导致其整体刚度相对较弱。在超大型集装箱绑扎桥的结构分析方面,曾骥等[1]通过对绑扎桥结构进行数值模拟,总结了极端工况下的高应力区域,并提出了相应的结构优化建议;王兴胜[2]基于数值建模对绑扎桥结构进行了振动响应分析,并针对不符合规范要求的部分结构提出了修改意见。然而,有关超大型集装箱船绑扎桥结构可靠性分析方面的研究成果较少,这是因为其功能函数没有显式表达式,难以通过一阶二次矩(first-order second moment,FOSM)或二阶可靠性方法(second-order reliability method,SORM)直接求得可靠性指标和失效概率,但可以采用蒙特卡罗(Monte Carlo,MC)方法进行计算。在MC方法中,可以采用失效概率样本点在全部样本点中的出现频率来表示失效概率,但这样总体计算成本很高,且计算效率较低。
为了解决这一问题,可以采用2种方法:一种是通过方差缩减技术,例如重要抽样(importance sampling,IS)法,减少抽样样本的总数,但该方法需要数以万计的样本点;另一种是采用近似模型技术来缩短单个样本点的计算时间。Schueremans等[3]采用定向采样方法建立了自适应的响应面代理模型,改进了MC方法,并对比了采用低阶多项式函数、样条曲线函数与神经网络来扩展响应表面进行可靠性分析的优劣,最终发现采用样条曲线函数和神经网络可以更准确地处理高维复杂结构的可靠性分析问题。Kang等[4]基于移动最小二乘的有效响应面法(response surface methodology,RSM)对MC方法进行了改进,该方法通过提高失效面附近样本点的权重系数,逐步逼近识别失效区域和最可能失效点(most probable point,MPP),从而降低了计算成本。Echard等[5]将改进Kriging近似模型与MC方法相结合,通过主动学习,令自适应的Kriging模型每次迭代更新的样本点均位于失效面附近,从而实现失效面函数的高度近似,故该方法对高可靠度模型具有很好的适应性。于雷等[6]和王正刚[7]将响应面作为近似模型,开展了结构可靠性分析。张崎[8]和黄晓旭等[9]利用Kriging近似模型完成了结构可靠性指标以及失效概率的计算。陈松坤等[10]和孟广伟等[11]将神经网络与MC方法相结合,开展了结构可靠度计算。Blagus等[12]通过对少数类样本点进行“过抽样”,合成了新的机器学习算法,即SMOTE算法。当利用代理模型对高可靠性指标的结构进行分析时,会出现抽样样本数量较多、失效样本点占比较少和拟合精度较差等问题,而SMOTE算法则可以解决传统过抽样算法通过简单地复制样本来增加少数类样本所导致的过拟合问题,从而能提高失效面的拟合精度。
本文拟应用SMOTE算法来增加失效面附近少数类样本点的数量,并对梯度提升决策树法(gradient boosting decision tree,GBDT)近似模型进行训练,然后结合MC方法完成结构可靠性的计算,用以为结构优化设计提供参考。
1 改进GBDT-MC方法
1.1 GBDT方法
GBDT方法是一种迭代的决策树算法[13]。假设有m个训练样本:



1.2 SMOTE算法
SMOTE算法是一种合成少数类数据的过抽

1.3 改进GBDT-MC方法的原理

综上所述,本文提出的改进GBDT-MC方法的原理为:首先,利用有限元方法计算少量样本点的信息,并筛选位于失效面附近的样本点;然后,运用SMOTE算法合成新的样本点并参与有限元计算,进而结合原有的样本点形成训练集;最后,对GBDT近似模型进行训练,并采用已训练的近似模型预测MC方法中的样本点信息,即可完成结构可靠性分析,从而显著提高计算精度和计算效率。
1.4 改进GBDT-MC方法的迭代流程


2 改进GBDT-MC方法的适用性验证
针对样本点的数量、失效概率值和可靠性指标β,对于改进GBDT-MC方法在结构可靠性分析问题中的准确性和稳定性,本文将结合文献[5,15]予以验证。
2.1 算 例1:一 个 具 有 解 析 表 达 式 的 失效面



图 3 非线性振荡器Fig. 3 Non-linear oscillator
表1所示为该算例6个随机变量c1,c2,m,r,t1,F1的分布类型及其分布参数。对于该问题,Echard等[5]采用改进的神经网络模型结合MC方法(back propagation-Monte Carlo,BP-MC)进行了计算。本文将采用与文献[5]相同的样本数量训练改进GBDT-MC模型,其对比结果如表2所示。
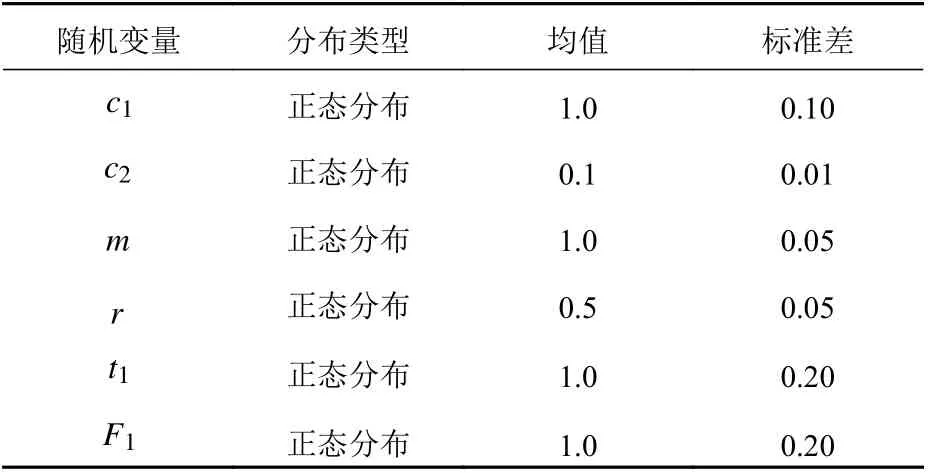
表 1 非线性振荡器设计变量特性Table 1 Stochastic characteristic of the non-linear oscillator

表 2 不同方法的计算结果对比(算例1)Table 2 Comparison of calculation results of different methods (example 1)
首先,建立该失效面的有限元模型,采用MC方法产生1×107个样本点,通过式(17)计算失效样本点的数量,然后通过式(16)即可计算该结构的失效概率和可靠性指标,结果如表2所示。
文献[5]中的BP-MC方法通过直接采样产生了1 281个样本点,进而计算得到响应集。本文通过均匀采样生成了881个样本点,计算得到初步响应集,并筛选了位于失效面附近的100个样本点;然后,结合SMOTE算法将次样本集扩大4倍,得到新的400个样本点的响应集,并结合原有响应集得到训练集。通过表2对比发现,相同数量的样本点参与训练时,改进GBDT-MC方法比BPMC方法的准确性更高。
2.2 算例2:十杆桁架结构


图 4 十杆桁架结构Fig. 4 10-bar truss structure
对于该问题,韦益夫等[15]采用移动最小二乘法(moving least square method,MLSM)改进了响应面法,并结合一阶二次矩方法建立了动态响应面模型。本文将采用与文献[15]相同的样本数量训练改进GBDT-MC模型,其对比结果如表3所示。
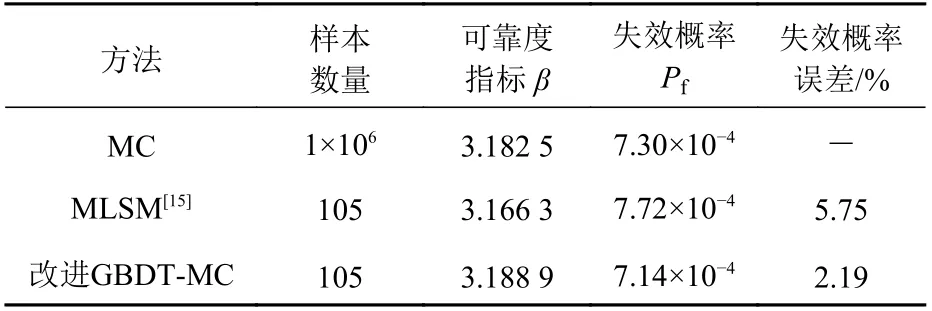
表 3 不同方法的计算结果对比(算例2)Table 3 Comparison of calculation results of different methods (example 2)
首先,建立该桁架结构的有限元模型,采用MC法产生1×106个样本点,进而基于有限元分析得到全部样本点的应力状态。通过式(18)计算失效样本点的数量,然后通过式(16)得到该结构的失效概率和可靠性指标,结果如表3所示。
文献[15]中的MLSM方法迭代了5次,响应面每次至少需要迭代中心点附近的21个样本点,总计105个样本点。本文通过均匀采样生成了65个样本点,计算得到初步响应集,并筛选了位于失效面附近的10个样本点;然后,结合SMOTE算法将次样本集扩大4倍,得到新的40个样本点的响应集,并结合原有响应集得到训练集。通过表3对比发现,相同数量的样本点参与训练时,改进GBDT-MC方法比MLSM方法的准确性更高。
3 基于改进GBDT-MC方法的超大型集装箱船绑扎桥可靠性分析
本文的结构可靠性分析对象为20 000 TEU超大型集装箱船07#绑扎桥,如图5所示。选取绑扎桥的板材厚度作为设计变量,每个设计变量均服从正态分布,共计选取14个设计变量(l1~l14),其中骨材和立柱的尺寸则作为已知量。各变量均值来自实测数据,标准差假定为均值的10%,具体信息如表4所示。边界条件为底端固支,静态绑扎力为175 kN,符合中国船级社的规范要求[16]。
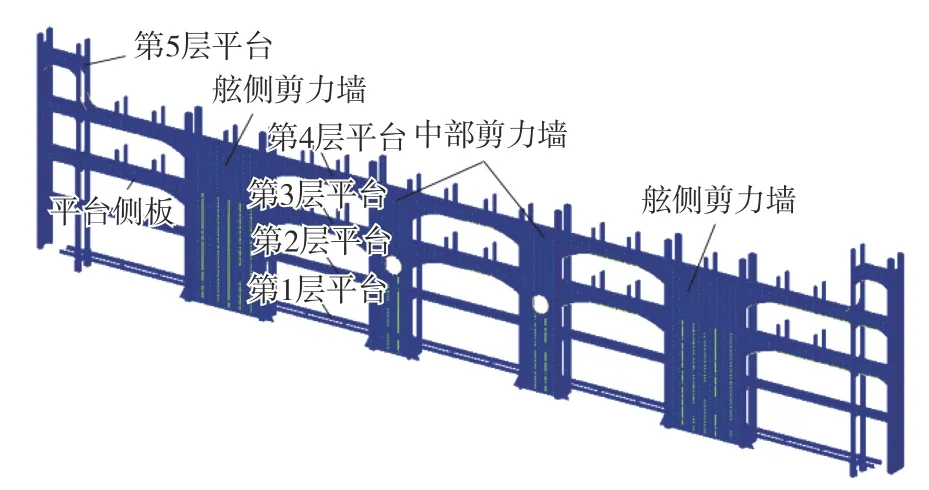
图 5 20 000 TEU超大型集装箱船绑扎桥结构Fig. 5 Lashing bridge of 20 000 TEU ultra large container ship
根据标准[16],绑扎桥结构的许用合成应力应不大于0.88倍的板材屈服极限。图5中绑扎桥的主要结构采用了AH36高强度钢,其屈服极限为355 MPa,则该结构的功能函数g(l)为

针对图5所示的绑扎桥结构,分别采用MC方法和改进GBDT-MC方法进行结构可靠性分析,计算对比结果如表5所示。
首先,建立该绑扎桥结构的有限元模型,采用MC法产生5×104个样本点,进而基于有限元分析得到全部样本点的应力状态。通过式(19)得到失效样本点的数量,然后使用式(16)得到该绑扎桥结构的失效概率和可靠性指标,结果如表5所示。

表 4 绑扎桥的设计变量Table 4 Design variables of the lashing bridge

表 5 计算结果对比Table 5 Comparison of calculation results
表5中的计算结果表明,该超大型集装箱船绑扎桥在静态绑扎力作用下的失效概率可达10-4量级,具有较高的可靠性。这是由于该结构采用了高强度钢,且考虑到工程实际中的环境载荷、建造工艺和人为操作等不确定因素,对该结构提出了较高的安全裕度要求。
本文通过均匀采样生成了220个样本点,计算得到初步响应集,并筛选了位于失效面附近的20个样本点;然后,结合SMOTE算法将次样本集扩大4倍,得到新的80个样本点的响应集,即总共调用300次有限元计算得到训练集。通过表5对比发现,改进GBDT-MC方法的失效概率误差为 3.5%,共花费2.55 h,而MC方法则需要416.7 h。因此,在允许的计算误差范围内,改进GBDT-MC方法可以大为缩减可靠性分析的计算时间。
4 结 论
针对复杂结构进行可靠性分析时单次计算耗时较长的问题,本文提出了一种改进GBDT-MC方法来计算失效概率。该方法通过Python库建立GBDT近似模型,通过实验生成较少的样本点,并通过SMOTE算法增加失效面附近的样本点数量,进而结合原有样本点得到训练集;通过对近似模型进行训练,完成对MC方法所产生样本的预测,最终完成失效概率的计算。另外,本文还基于2个算例验证了改进GBDT-MC方法的适用性,并将该方法应用到了超大型集装箱船绑扎桥结构的可靠性分析中,结果表明:
1) 本文提出的改进GBDT-MC方法适用于结构的可靠性分析,尤其适用于高可靠性指标的结构。
2) 利用SMOTE算法对失效面附近的样本进行插值,可以提高少数类样本的占比,有效减少总抽样次数,从而缩短计算时间。
3) 改进GBDT-MC方法可以对失效面进行高度近似拟合,从而大为提高计算精度。
需要指出的是,随着训练集样本点数量的增加,改进GBDT-MC方法的计算精度也将随之提高。同时,每次参与训练的样本点信息均可保存于模型中,并与优化算法进行高效结合,以便为后续的可靠性优化设计提供支持。
