基于非对称齿形的塑料齿轮磨损性能研究*

2020-05-25杨维松王淑坤

机电工程 2020年5期

关键词：角为齿形轮齿

杨维松,王淑坤

（1.长春理工大学机电工程学院，吉林长春 130022；2.东方通信股份有限公司，浙江杭州 310053）

0 引言

大额现金循环模块用于钞票的连续存取、传输和鉴别，其传动系统主要由齿轮构成。大额现金循环模块由于涉及到现金，只能在保险柜这样空间狭小、温度高、不能进行润滑的环境下工作，而金属齿轮又无法达到使用要求。

与金属齿轮相比，热塑齿轮具有质量轻、噪声小、不锈蚀、可在无润滑条件下工作的特点，可满足大额现金循环模块的工作要求。但塑料为粘弹性体,失效形式和失效机理都与金属齿轮有很大区别；尤其在开式传动中,轮齿磨损是塑料齿轮的主要失效形式[1]。

因此，如何减小齿轮的磨损，提高热塑齿轮的寿命一直以来成为研究的主要课题。邱良恒等[2-3]通过计算分析，提出了通过改善材料导热性提高塑料齿轮寿命的方法；FRANKLIN[4]通过干往复滑动条件下进行了磨损试验，提出了通过降低材料的摩擦系数，可减小摩擦热从而提高耐磨性；YOUSEF等[5-8]通过实验分析提出了，通过采用合适的材料可以降低摩擦提高齿轮的疲劳强度和抗磨损性，并可通过改性获得更好的性能[9-11]；TABURDAGITAN[12]对圆柱直齿轮的摩擦生热过程进行了分析，得出了滑动率和接触强度对齿面温升有直接影响的结论；DENG等人[13]通过对提高非对称齿形弯曲载荷能力的研究，得出了“增加非对称齿轮工作齿侧的齿形分度圆压力角，可明显减小非对称齿轮齿根弯曲应力并提高齿根刚度”的结论；KAPELEVICH等[14]基于采用较大压力角工作面和较小压力角非工作面的设计思想,分析得出了采用该种设计的齿轮可以提高齿轮齿根弯曲强度，减小齿轮体积，降低齿轮振动和噪声的结论。

以上研究分析了影响齿轮寿命的主要因素，并从改进材料和优化齿轮设计的方面做了大量工作，得出了通过改进材料有益于提高齿轮寿命，以及通过改进齿形有益于提高齿根弯曲强度及降低噪声的结论。但目前尚没有通过齿形变化增加工作面压力角，以提高热塑齿轮寿命的报导。

针对金融机具大额现金循环模块的工作特点，笔者设计工作面35°非工作面20°的双压力角非对称热塑齿轮优化改进方案，并与现有标准压力角齿轮进行对比分析，确定改进方案对齿轮磨损的影响规律。

1 塑料齿轮工作齿面运动学动力学分析

1.1 塑料齿轮工作齿面磨损的数学建模

工程塑料作为一种粘弹性体材料，其磨损由粘着磨损和磨料磨损组成，磨损量可由以下公式确定：

W=K×P×V×t

（1）

式中：W—磨损量，mm3；K—磨损因子，（mm3/N·m）×10-8；P—接触面压强，MPa；V—相对滑动速度，m/s；t—磨损时间,s。

工程塑料的磨损同时包括粘着磨损和磨料磨损，因此建立数学模型运用Matlab软件分析塑料齿轮啮合时的磨损时必须考虑接触应力、相对滑动速度和摩擦热流的影响。

1.2 非对称塑料齿轮传动的理论基础

1.2.1 非对称塑料齿轮齿廓线生成原理

非对称塑料齿轮与对称塑料齿轮的主要区别为非对称塑料齿轮轮齿两侧的齿廓形状不同，当工作侧的发生线沿半径为rbd的工作侧基圆圆周做纯滚动时，直线上点M形成的渐开线就是轮齿工作侧齿廓线。同理，非工作发生线沿半径为rbc的非工作侧基圆圆周做纯滚动时，直线上点N形成的渐开线为轮齿非工作侧齿廓线。

非对称塑料齿轮齿廓线的方程式为：

（2）

θMd=tanαMd-αMd;θNc=tanαNc-αNc

（3）

式中：rM—轮齿工作侧渐开线上任意点M的向径；rN—轮齿非工作侧渐开线上任意点N的向径；αMd—轮齿工作侧齿廓曲线上M点处的压力角；αNc—轮齿非工作侧齿廓曲线上N点处的压力角；θMd—轮齿工作侧齿廓曲线上M点处的展角；θNc—轮齿非工作侧齿廓曲线上N点处的展角。

1.2.2 非对称塑料齿轮的正确啮合条件

由于非对称齿轮轮齿两侧的齿形不同，要保证非对称齿轮正确工作，就必须同时保证啮合的非对称齿轮相邻两齿齿廓沿公法线方向的距离在工作侧和非工作侧分别相等，即要保证一对非对称塑料渐开线齿轮的正确啮合，必须保证两齿轮在工作侧和非工作侧的基节分别相等，即：

（4）

（5）

由上式可得，当两个啮合齿轮模数相同的非对称双压力角渐开线齿轮正确啮合时，两齿轮轮齿在工作侧和非工作侧的分度圆压力角度一定分别相等，即：

αd1=αd2;αc1=αc2

（6）

式中：m—啮合齿轮分度圆模数；z1/z2—齿轮1/齿轮2的齿数；αd1/αd2—齿轮1/齿轮2工作侧的分度圆压力角；dbd1/dbd2—齿轮1/齿轮2工作侧齿廓基圆直径；αc1/αc2—齿轮1/齿轮2非工作侧的分度圆压力角；dbc1/dbc2—齿轮1/齿轮2非工作侧齿廓基圆直径。

1.3 不同齿形塑料齿轮工作齿面接触应力分析

根据赫兹理论，物体表面之间有相同距离的点在公切面上会形成近椭圆形的区域[15-16]。因此，同材料啮合的对称齿轮和非对称塑料齿轮工作齿面上的平均接触压强，都可以根据赫兹理论建立以下公式：

（7）

式中：Pa—平均齿面接触压强；FNC—作用于齿面的法向载荷；E—齿轮材料的弹性模量；b—齿轮宽度；V—齿轮材料泊松比；ρec—轮齿啮合点的等效曲率半径。

式（7）中，轮齿啮合点等效曲率半径ρec可由以下公式求得：

（8）

（9）

（10）

式中：ρe1—轮齿啮合点主动齿轮曲率半径；ρe2—轮齿啮合点从动齿轮曲率半径；gyM—齿面上任意接触点M与节点在啮合线上的距离。

设此点在主动轮上的半径为rM，则M点在齿轮啮合线上与节点的距离表示如下：

（11）

上式中，上面一组符号适用于主动轮的齿顶或从动轮的齿根接触点，下面一组符号则适用于主动轮的齿根或从动轮的齿顶接触点。

公式（7）中，作用于齿面的法向载荷FNC可以表示如下:

（12）

式中：T1—从动轮轴的转矩；K—齿轮啮合区内齿间载荷分配系数（常取K=0.5）；z1—主动轮齿数；z2—从动轮齿数；rM—啮合点在主动轮上的半径；α—啮合齿侧压力角。

由于轮齿工作时的交替啮合而产生的齿间载荷分配和轮齿啮入及啮出冲击的影响，使得轮齿齿面的接触压力分布是不均匀的，双压力角塑料齿轮啮合图如图1所示。

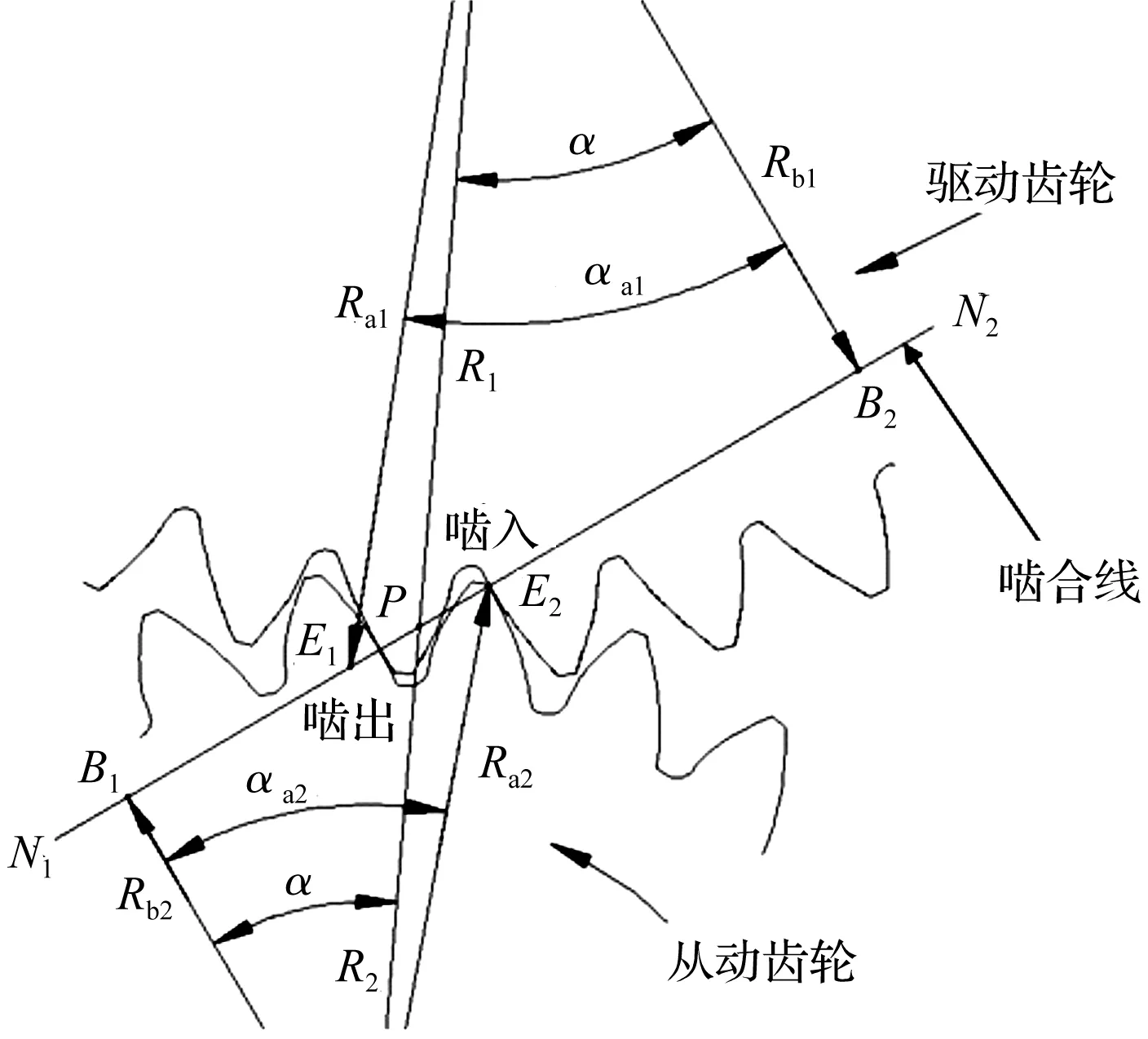
图1 双压力角塑料齿轮啮合图

笔者通过以上公式对轮齿工作面平均接触压强进行了仿真分析，得到大齿轮为主动轮的仿真结果如图2所示。

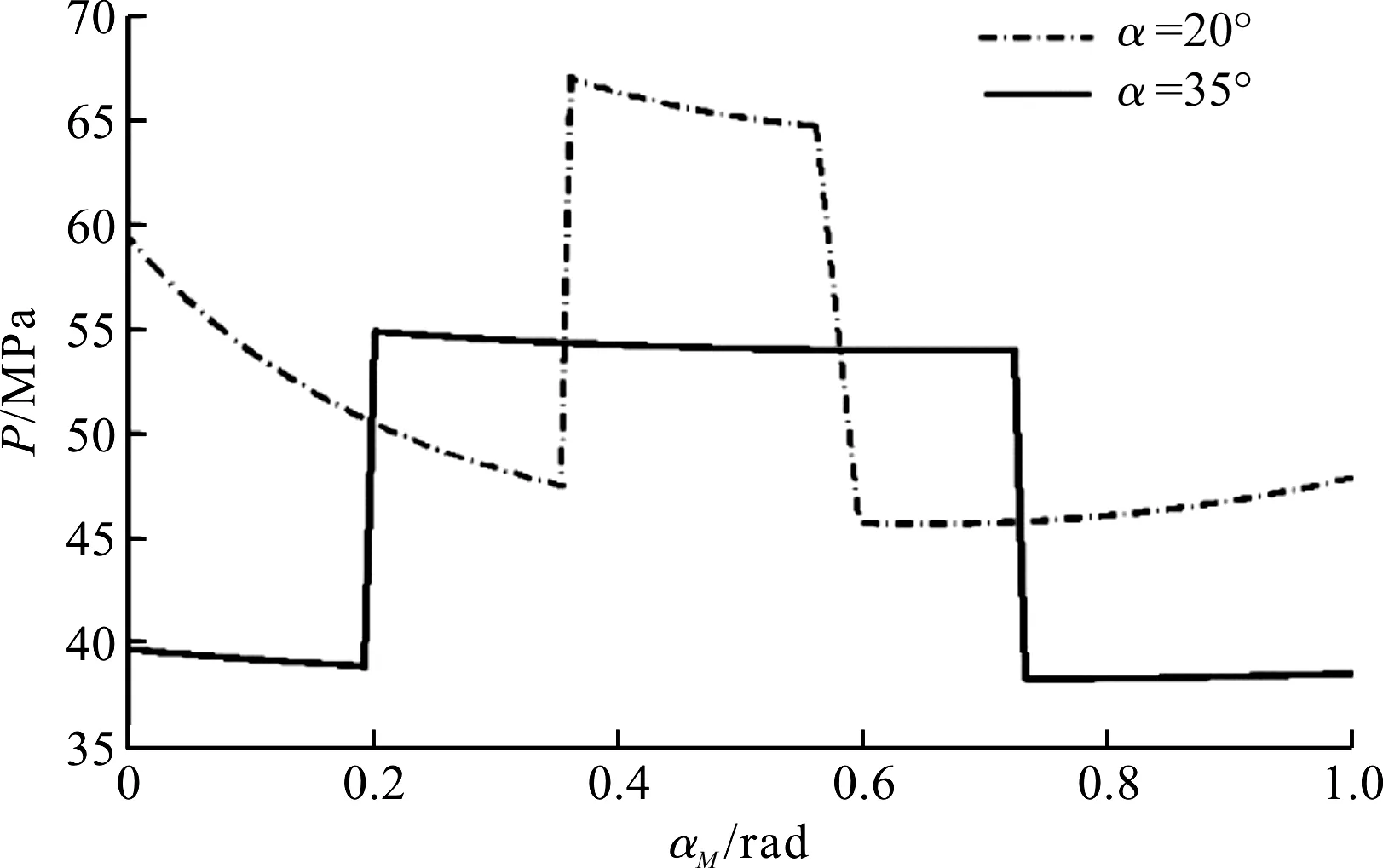
图2 不同齿形塑料齿轮工作面归一化压力角接触压力分布

图2中，坐标从左向右依次为双齿啮合主动齿轮齿根啮入点、单齿啮入点、单齿啮出、双齿啮合主动大齿轮齿顶啮出点。工作齿面压力角为35°非对称齿轮和工作齿面压力角为20°的标准齿轮轮齿工作面平均接触压强由图1中的Pa（35°）和Pa（20°）分别表示。

由图2可以得出，齿轮从齿根啮入到齿顶啮出齿面平均接触压强在非对称齿轮和标准齿轮下的变化规律和分布。对于压力角为20°标准塑料齿轮，工作齿面平均接触压强的最大值出现在单齿啮合区，达到68 MPa；对于工作齿面压力角为35°非对称塑料齿轮，同样在单齿啮合区达到56 MPa工作齿面平均接触压强的最大值，但相较于标准齿轮，工作齿面平均接触压强无论是单齿啮合区还是双齿啮合区，都呈明显下降趋势。

1.4 不同齿形塑料齿轮工作齿面相对滑动速度分析

对称齿轮和非对称塑料齿轮的齿轮渐开线都由发生线在基圆上纯滚动而形成，轮齿在实际工作啮合过程中存在相对滑动，而且轮齿在不同的啮合点相对滑动速度不同，在节线附近的相对滑动速度最小，在节线处的相对滑动速度为0。

由式（1）可知，在塑料齿轮工作齿面正压力的作用下，啮合点齿面磨损量与相对滑动速度成正比。而相对滑动速度随齿轮转速变化而变化，不能正确对比齿轮间相对滑动速度的大小，因此笔者通过引入相对滑动率来标定齿轮间相对滑动速度大小。当一对齿轮啮合时，在啮合区中任意点的齿面磨损量之比等于其齿面相对滑动率之比[17-18]。

基于此，塑料齿轮的齿面滑动磨损程度可用齿面相对滑动率来反映。从齿轮轮齿的运动学分析齿轮的相对滑动，可以得到塑料齿轮传动的齿面某个时刻，在M点啮合的相对滑动速度表达式、相对滑动率。

M点的相对滑动速度为：

（13）

相对滑动率为：

（14）

（15）

式中：vm1/vm2—主动齿轮/从动齿轮在M点的切向分速度；i21—从动齿轮和主动齿轮的齿数比；rm1—主动齿轮啮合半径；αm1—主动齿轮在啮合点的压力角；r1/r2—主动齿轮/从动齿轮分度圆半径；α—齿轮分度圆压力角。

根据以上推导，笔者选择模数为1，主动轮齿数为36，从动齿轮齿数为24，对工作齿面压力角为35°的非对称齿轮和工作齿面压力角为20°的标准齿轮，在啮合区中的相对滑动率进行仿真。

其中，小齿轮归一化啮合压力角相对滑动率绝对值如图3所示。

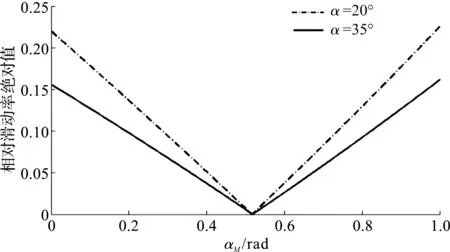
图3 小齿轮归一化啮合压力角相对滑动率绝对值

大齿轮归一化啮合压力角相对滑动率绝对值如图4所示。

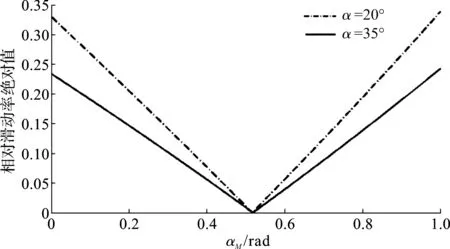
图4 大齿轮归一化啮合压力角相对滑动率绝对值

由图（3，4）可以看出：从节点位置向齿轮齿项和齿根，齿轮的相对滑动率绝对值随着啮合压力角的变化逐渐增加；同时，工作齿面压力角为35°的非对称齿轮比工作齿面压力角为20°的标准齿轮相对滑动率绝对值减小，在齿顶和齿根部分相对滑动率降低更加明显。

由此可以得到结论：与标准齿轮相比，采用大压力角工作面的非对称齿轮，有利于减少齿面的相对滑动率。

1.5 不同齿形塑料齿轮工作齿面摩擦热流密度分析

对于塑料齿轮，由于材料性能上的差异,其失效形式已发生改变。与金属齿轮相比，塑料齿轮具有导热、耐热性差、热膨胀因数大等缺点,并且容易受到温度的影响。YELLE等[19]在充分研究了塑料热塑性对直齿轮传动影响的基础上，提出了齿轮传动中啮合温度及疲劳强度的预测方法。

假定主动轮和从动轮的摩擦热流密度qc的分配是均等的,则在任何啮合位置，轮齿接触点C处的主、从动轮的摩擦热流密度qc1和qc2可分别表示为：

（16）

式中：β—摩擦热流密度的分配因子；μc—摩擦因数；Pnc—齿面接触压力；Vgc—齿面的相对滑动速度；η—摩擦能转化为热能的系数，其中β1+β2=1。

设齿轮1为主动齿轮，模数1，齿数36，材料POM，从齿根啮入到齿顶啮出；齿轮2为从动齿轮，模数1，齿数24，材料POM，从齿顶啮入到齿根啮出。

由于两种材料相同,热分配系数β1=β2=0.5，则工作齿面压力角为35°的非对称齿轮和工作齿面压力角为20°的标准齿轮，在啮合区归一化啮合压力角热流密度如图5所示。

图5 齿轮啮合区归一化压力角摩擦热流密度

根据图5可以得知：摩擦热流密度在齿轮啮合区的节点处为0，随啮合点从节点向齿顶和齿根移动，摩擦热流密度逐渐增加；同时，在齿啮合区的各点处，工作齿面压力角为35°的非对称齿轮比工作齿面压力角为20°的标准齿轮，摩擦热流密度会减小，减少幅度在齿根和顶处更明显。

由此可以得到结论：与标准齿轮相比，采用大压力角工作面的非对称齿轮，有利于减少齿面摩擦生热。

1.6 塑料齿轮不同齿形工作面齿面齿廓干涉磨损分析

对于渐开线齿轮传动而言，小齿轮和大齿轮的工作齿廓曲线都是渐开线。当齿轮齿基圆大于根圆时，基圆到根圆这部分齿廓曲线为非渐开线齿廓，使大齿轮齿顶渐开线部分的齿面与小齿轮齿根一部分非渐开线的齿面相接触，即产生齿廓干涉[20]。

齿轮齿基圆与根圆的差为：

（17）

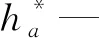
由式（17）可知，根圆与基圆直径差的大小与齿数和工作齿面齿形有关。

对于模数为1的齿轮，当其工作齿面齿形压力角为20°的标准齿轮，齿轮齿数在34齿以下时，根圆直径小于基圆直径，工作齿面齿形部分曲线不是渐开线，需要经过修形处理；而热塑齿轮一般都为模具成形，在齿根处的收缩比最大，很难达到理想值，从而会出现顶死或不正常啮合的磨损情况；当非对称齿轮的工作齿面齿形压力角为35°时，齿轮齿数在15齿时，根圆直径已大于基圆直径，整个轮齿曲线全部是渐开线，从而可以消除由齿面修形引起的齿廓干涉。

由此可以得到结论：与标准齿轮相比，采用大压力角工作面的非对称齿轮，有利于减少和防止塑料齿轮的齿廓干涉，减少工作面齿面齿廓干涉磨损。

2 齿轮结构设计和制造

2.1 非对称塑料齿轮材料

笔者采用的齿轮制备材料为美国尔特普（RTP）公司的聚甲醛（RTP0800-POM），按照ASTM D-3702，采用ECT1604设备（美国），采用“Thrust Washer” Wear Test实验测得RTP0800型号聚甲醛的具体性能参数，如表1所示。

表1 磨损实验参数

2.2 非对称塑料齿轮相关参数选取

当齿轮材料为RTP0800聚甲醛，笔者选取工作齿面压力角为35°的非对称齿轮，和工作齿面压力角为20°的标准齿轮时，不同齿数齿轮的运行参数如表2所示。

表2 不同齿数齿轮的运行参数

2.3 齿轮结构设计、制造

根据齿轮计算分析结果，由软件Pro/E生成三维模型，笔者委托东莞市超骏齿轮有限公司完成齿轮注塑加工，齿轮由模具加工成型。

齿轮成型参数如表3所示。

表3 齿轮成型参数

3 齿轮实验及结果分析

根据表2中的参数，按表3的加工工艺，笔者对36齿及24齿的非对称齿轮及35齿及22齿的对称齿轮进行注塑加工；将样件装在东方通信开发的TCRMe1000大额循环模块测试机上，进行压力测试。

TCRMe1000大额循环模块测试机如图6所示。

实验中，分别采用由POM制备的非对称塑料齿轮和标准塑料齿轮，同时安装在测试样机传动系统中进行测试，并且保证各对齿轮受力情况基本相同；经压力测试后，笔者考查工作齿面齿形压力角为35°的非对称塑料齿轮和工作齿面齿形压力角为20°的标准塑料齿轮对轮齿的磨损情况，并记录各阶段的数据。

图6 TCRMe1000大额循环模块测试机

当齿轮在测试机上持续工作3 229 h后，笔者统计24齿工作齿面齿形压力角为35°的非对称塑料齿轮和22齿工作齿面齿形压力角为20°的标准塑料齿轮各阶段磨损量。

测试时间对塑料齿轮磨损率和单齿磨损质量的影响，如表4所示。

表4 测试时间对塑料齿轮磨损率和单齿磨损质量的影响

由表4可得：齿轮磨损率随着测试时间的增加而增大，齿轮的单齿磨损量随测试时间增加而增大；当测试时间为3 229 h时，工作齿面齿形压力角为20°的标准塑料齿轮的磨损率为1.37%，而压力角为35°的非对称塑料齿轮的仅为0.68%。同时测试后压力角为35°的非对称塑料齿轮平均每齿磨损明显小于标准塑料齿轮。这说明选用非对称塑料齿轮的磨损弱于标准塑料齿轮。

以上结果说明，相对于标准齿形塑料齿轮，工作齿面齿形压力角为35°非对称塑料齿轮，在接触应力、相对滑动速度、摩擦热流密度、齿廓干涉磨损方面均有优势；并且在实际实验中，所得到的数据也与理论分析的结果相一致。