基于LCD与峭度-能量比准则的滚动轴承故障诊断研究*

杨文志，张茹军，安文斌

（内蒙古科技大学 机械工程学院，内蒙古 包头 014010）

0 引 言

滚动轴承作为机械传动部件中重要的组成成分，一旦发生故障将会对整个机械传动系统造成巨大的影响，因此开展滚动轴承故障诊断的研究非常必要。

局部特征尺度分解是一种新的信号分解方法，近年来在非平稳、非线性信号的分解中得到广泛应用，该方法具有以下优点：（1）提高了运算速度；（2）相对于EMD、LMD、ITD等方法，LCD的迭代次数更少，在抑制端点效应、模态混叠等方面更有优势，具有更好的时频局部化特性[1]。

文献[2]提出了LCD与排列熵相结合的故障诊断方式；文献[3]提出了LCD与基本尺度熵相结合的故障诊断方式；文献[4]提出了将LCD与互近似熵相结合的故障诊断方式；许多学者采用了EMD、VMD等与各种熵或者能量相结合的方式，来诊断齿轮或滚动轴承的故障[5-7]。多特征值融合可以弥补单一特征的局限性，但是大量的特征值结合容易导致特征冗余，计算量大，会影响故障分类的结果。因此，峭度准则、相关系数法、特征加权等方式被应用于筛选有效分量。

本文将采用LCD对滚动轴承信号进行分解，根据峭度-能量比准则，计算各ISC分量的Kr值，选取Kr值较大的ISC分量作为有效分量，计算其能量熵和多尺度熵，以此作为特征向量。

1 理论介绍

1.1 LCD分解方法

LCD方法是将复杂的振动信号分解成具有不同能量并且相互独立的ISC分量，分解时需要满足以下条件：

（1）在寻找极值点过程中，使得所有相邻两个极值点保证符号互异；

（2）在构建基线信号前设定点（xk,τk）,其中：k=1,2,3,…,M；该点代表极值点以及对应的时刻，时刻点τk+1在左右相邻两个极值点构成的线段上相对应的函数值为Ak+1，函数值Ak+1与极小值xk+1的关系是比值近似不变。

函数值Ak+1的表达式如下式所示：

（1）

通过以上条件保证了分解形成的ISC分量符合正弦曲线特性，使得其在任意两个相邻极值点之间具有单一模态。

分解流程如图1所示。

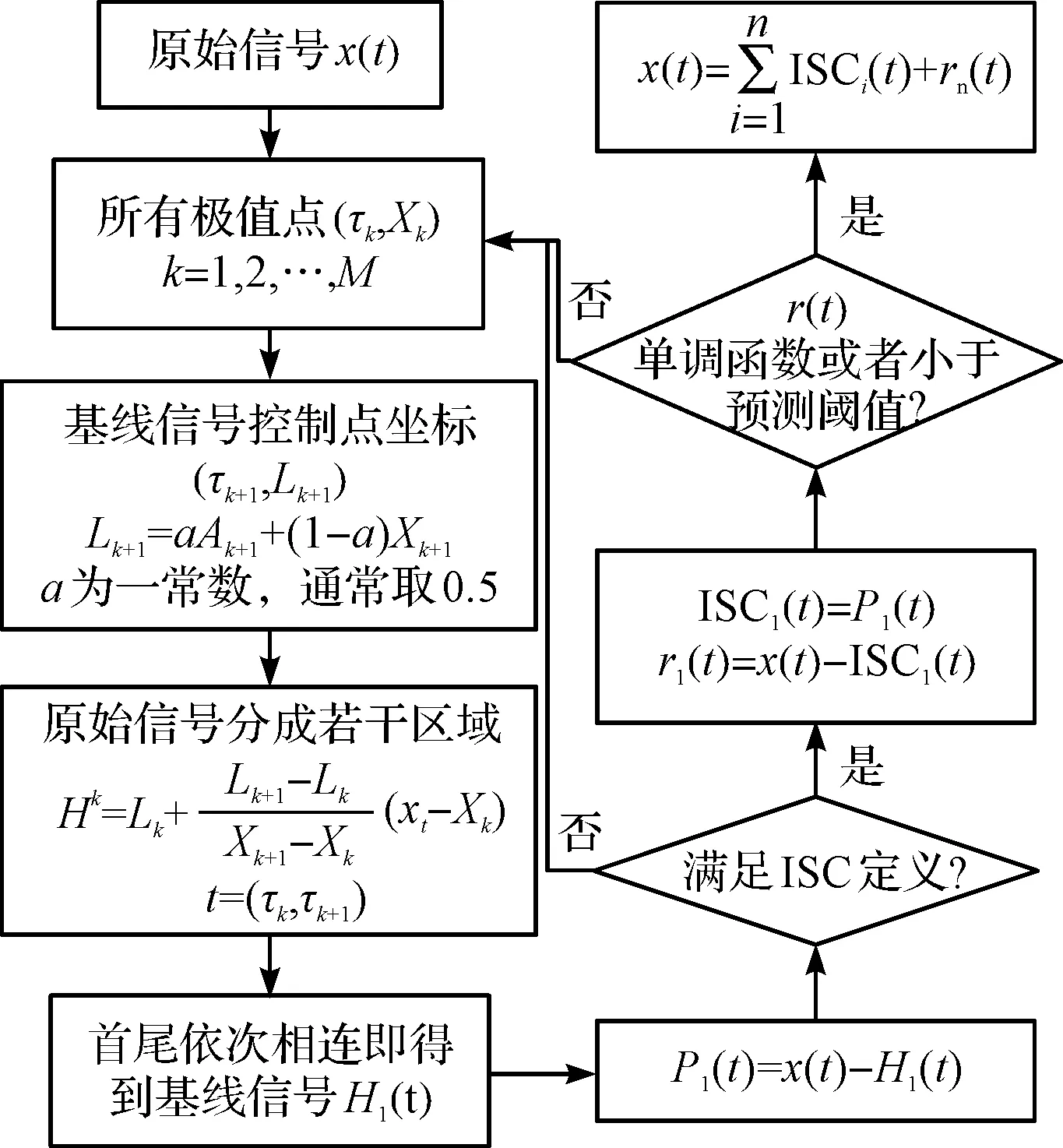
图1 LCD分解流程图

LCD分解的结束条件有标准偏差法、阈值法和极值单调性这3种，本文LCD分解结束采用的是极值单调性方式。

从美国Spectra Quest公司机械故障综合模拟试验台采集滚动轴承内圈故障数据，进行LCD分解后获得的波形图如图2所示。

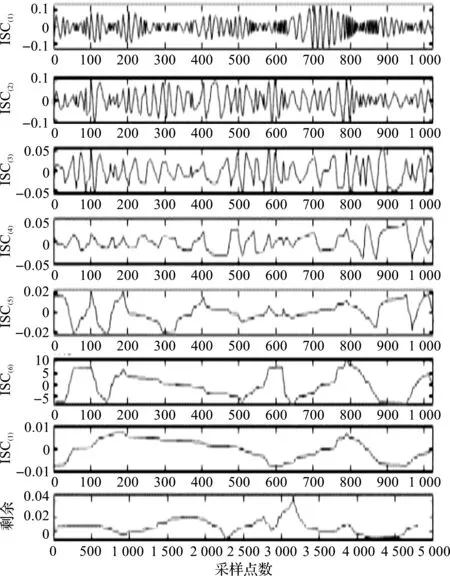
图2 LCD分解图

1.2 峭度-能量比准则

信号经LCD分解为多个ISC分量，分解的ISC分量的频率是由高频到低频产生的，其幅值和频率都会有所衰减，能量逐渐降低，且容易在低频区产生虚假分量。

能量比系数表达如下式所示：

（2）

式中：ε—能量比系数；EISC（i）—不同分量具有的能量；Ex—总能量。

分解形成的ISC能量比值是不同的，单纯采用能量比准则提取有效分量存在一定误差，因此，笔者将能量比与峭度值相结合来综合分析。

将其定义为ISC分量的Kr值为：

Kr=αK+（1-α）ε

（3）

式中：K—ISC分量的峭度值；ε—不同ISC分量的能量比；α—不同的ISC分量的峭度值对Kr值的权值度。

计算各个ISC分量峭度、能量比和Kr值，如表1所示。

表1 各ISC分量峭度、能量比和Kr值

表1说明：ISC1分量具有的Kr值约为1.5，ISC2分量与ISC3分量的Kr值约1，而其他分量的Kr值≤0.5。

因此，笔者选用ISC1、ISC2与ISC3这3个分量的特征。

1.3 能量熵

LCD信号分解将原始故障信号分解成具有不同能量的分量，各分量的能量依次减少，残余分量的能量很小，因此可以忽略不计。

能量熵定义如下式所示：

（4）

式中：E—不同分量上具有的幅值能量；Esum—信号的总能量；pi=Ei/Esum。

采用滚动轴承内圈故障信号进行LCD分解，分解后能量熵如表2所示。

表2 LCD能量熵

1.4 多尺度熵

多尺度熵是基于样本熵的一种改进方法，用于描述时间序列在不同尺度熵的无规则程度[8]。它可全面反映信号的复杂度,能很好地区分不同故障,被广泛应用到机械故障诊断领域[9-10]。

多尺度熵的计算步骤如下：

（1）进行粗粒化计算，以获得新的时间序列：

（5）

式中：x（i）—原始序列；τ—尺度因子，当尺度τ=1时，即为原始时间序列。

（2）将新的时间序列然后组成一组矢量，其中：Y（τ）i=1,2,N-m+1；

（3）计算不同矢量下差值的绝对值最大值的距离d[Y（τ）（i）,Y（τ）（j）]，其表达式为：

d[Y（τ）（i）,Y（τ）（j）]=
maxk=0,…,m-1（|yτ（i+k）-yτ（i+k）|）

（6）

（5）多尺度熵定义：

（7）

式中：τ—尺度因子；m—嵌入维度；r—阈值。

多尺度熵中参数的变化将会影响最后的输出结果，参数有尺度因子τ、嵌入维度m和阈值r。通常取r的值为0.1SD～0.5SD（SD是原始数据的标准差），尺度因子τ取值范围为120。通过对比分析发现：当尺度因子τ取9时，滚动轴承各故障的样本类间距离值为最大。

因此，此处选择τ为9。

计算滚动轴承内圈故障下的多尺度熵，如图3所示。

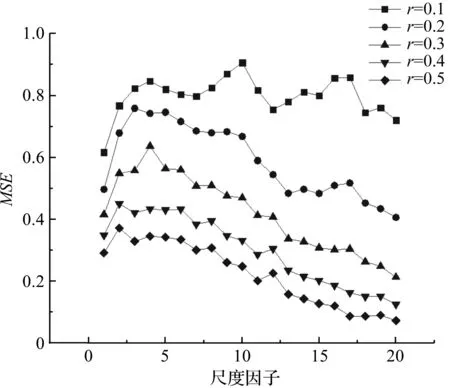
图3 多尺度熵曲线

由于分解形成第1个模态具有的信息是最全面的，笔者选用第1个模态的多尺度熵。参考其他文献，笔者设定m=2，τ=20。

图3说明：r取值越小，MSE值整体越大，r取值越大，MSE值整体越小；但是当r的取值越小时，MSE曲线波动较为明显。

因此，综合考虑笔者取r=0.2。

选用滚动轴承内圈故障数据分解形成的ISC分量计算多尺度熵，如表3所示。

表3 ISC1的多尺度熵

1.5 SVM原理

支持向量机被广泛应用于设备状态监测和寿命预测等方面，其是在线性最优分类超平面的基础上，在线性情况下，构造出一个最优超平面。它将需要解决的问题转化为求取凸二次规划问题中的最大间隔和最小化错分程度，通过引入惩罚参数c来权衡两者的比重。

支持向量机给设样本集为（xi,yi），其中：n—数据个数，i=1,2,3,…,n；xi—类属性，xi∈Rm；yi—类标记，yi∈（1,-1）。

支持向量机将低维空间的输入映射到高维空间，寻找最优超平面。

超平面定义如下:

（8）

式中:ai—拉格朗日乘子;K（x,xi）—核函数;b—偏置。

本文选用高斯径向核函数为:

（9）

2 滚动轴承故障诊断步骤

滚动轴承故障诊断的具体步骤如下：

（1）对采集到的振动数据进行LCD分解，获得不同的ISC分量；

（2）对LCD分解产生的分量，运用峭度-能量比准则提取有效分量；

（3）计算有效ISC分量的能量熵，并对能量熵进行加权处理，获得不同权值比重的能量熵；

（4）计算有效ISC分量的多尺度熵；

（5）进行融合构建特征向量，输入支持向量机进行分类识别。

3 滚动轴承故障诊断实验及分析

滚动轴承实验数据来自美国Spectra Quest公司机械故障综合模拟试验台。机械故障综合模拟试验台如图4所示。

图4 机械故障综合模拟试验台

笔者选用6205-2RS深沟球轴承作为测试轴承。测试轴承滚珠个数为9个，滚动体直径为7.94 mm,轴承径节为39.04 mm；实验室电机转速1 500 r/min，采样频率为33 kHz，采样点数4 800。

参考文献[11-13]中的样本数目，在滚动轴承正常、内圈故障、外圈故障、滚动体故障这4种状态下，分别采集60个样本，共获得240个样本数据。在每种状态下，随机选择30组数据作为训练样本，剩余的30组数据作为测试样本。

上述滚动轴承振动信号经过LCD分解，共获得8个ISC分量。运用峭度-能量比准则，筛选其中的3个有效分量，计算其能量熵与多尺度熵，然后输入SVM中进行分类，最后得到结果。

根据上述诊断步骤，可得到滚动轴承故障诊断准确率如表4所示。

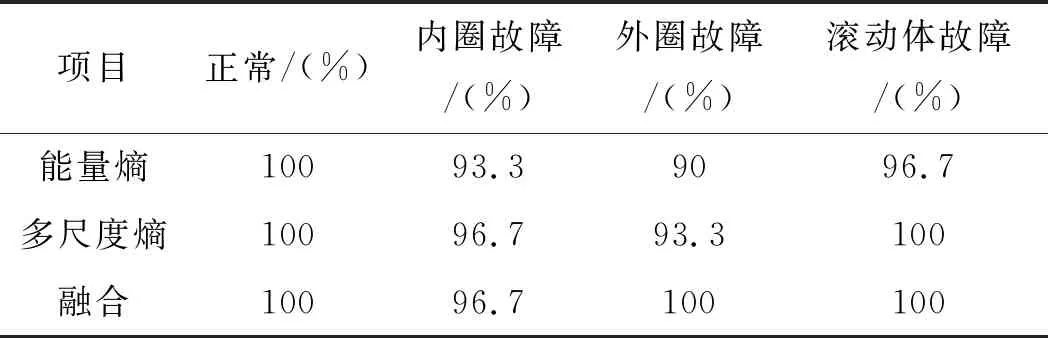
表4 故障诊断准确率

再将上述滚动轴承振动信号经过LCD分解，共获得8个ISC分量，分别计算8个ISC分量的能量熵和多尺度熵，并输入SVM进行分类，最终得到滚动轴承的故障诊断结果，如表5所示。

表5 故障诊断准确率

由表（4,5）数据可以说明：

（1）使用多特征进行故障诊断的准确率高于单一特征的准确率；

（2）筛选后的ISC有效分量提高了滚动轴承故障诊断的准确率。

4 结束语

采用LCD信号分解与峭度-能量比准则相结合的方法，本文进行了滚动轴承故障诊断：首先采用LCD对滚动轴承信号进行了分解，根据峭度-能量比准则，计算了各ISC分量的K_r值，然后选取K_r值较大的ISC分量作为有效分量，计算了其能量熵和多尺度熵，以此作为特征向量；该方法提高了故障诊断的准确率。得到结论如下：

（1）将能量熵、多尺度熵分别作为滚动轴承的故障特征，并对比两者的故障诊断准确率，结果表明：内圈为6.6%，外圈为10%，滚动体为6.7%；

（2）运用峭度-能量比准则筛选ISC分量，能够提高滚动轴承的故障诊断准确率；结果表明，滚动轴承内圈、外圈的故障诊断准确率分别提高了3.4%，3.3%。