时间尺度对平原感潮河网水动力水质模拟精度的影响
2020-05-25朱晓琳李一平许益新程一鑫朱向宇
朱晓琳,李一平,许益新,程一鑫,朱向宇
(1.河海大学环境学院,江苏 南京 210098; 2.广东省环境科学研究院,广东 广州 510045;3.清水源(上海)环保科技有限公司,上海 200061)
随着城市化的发展,平原河网地区水环境污染越来越严重,多地通过调水引流来增强河网内部水流循环,改善水环境[1]。水动力水质模型可较好模拟调水引流过程,是分析引调水对区域水动力水质改善效果的良好工具[2-6]。模型不确定性是当今数值模拟领域中的重要问题,不确定性来源于模型结构不确定性、参数不确定性和输入条件不确定性[7]。输入条件不确定性的研究主要集中在边界输入条件不确定性方面,Linden等[8]研究了进水温度、风速和进出水库流量对水库水动力水质模型模拟结果的影响;李一平等[9]研究了湖泊水动力模型中出入湖流量、风速、风向3个边界输入条件和初始水位1个初始输入条件对模型水位、水龄以及流场模拟结果的影响与贡献;曹引等[10]分析了二维水动力学模型参数、边界条件及两者共同作用导致模型模拟水位的不确定性,并利用偏秩相关分析方法分析了模型参数和边界条件对模拟水位的敏感性。目前对于模型边界条件不确定性的研究多集中于水库、湖泊或单条河流,由于这些区域多采用泵引,入流边界受时间变化影响较小,这就造成在筛选入流边界序列时,仅局限在最大和最小边界值区间内,并不适用于平原感潮河网地区,平原感潮河网地区受潮汐影响水动力情况变化剧烈,多利用潮位和内河水位差开闸引调水[11],边界输入条件与引调水时间关联性较为密切。在野外同步监测过程中,除了关注监测仪器的精度,设计监测方案时还需要考虑监测频率的选取,监测频率选取过小会增加工作量且对后期的运算数据处理造成麻烦,选取过大会导致实测数据失真,故对平原感潮河网地区来说,不同时间尺度边界入流条件对模型水动力水质模拟精度的影响不能忽略。
本文以典型平原感潮河网地区的张家港市中部为研究区域,利用野外同步监测数据、自动高频监测数据、常规监测资料以及数值模拟技术,构建水动力水质模型,研究不同时间尺度边界入流条件对水动力水质数学模型模拟精度的影响,以期为平原河网地区实地监测和河道管理提供参考。
1 研究区域概况
张家港市隶属于江苏省苏州市,共河网水系属太湖流域澄锡虞水系,为典型的平原感潮河网地区,利用长江和内河水位差控制沿江闸站启闭,引水量和引水时间受长江潮位影响。天生港站为长江张家港段潮位代表站,水位高低主要受上游大通来水量和沿海潮汐双重影响,其潮位属不规则半日周期潮,每日有2次高潮和2次低潮,连续2次高潮差别较大,2次低潮则差别较小[12],大潮主要出现农历初三和十八前后[13]。张家港市利用下午的高潮引水,引水时间一般在14:00~20:00之间,经1 h左右达到最大值,引水过程持续2~3 h。
选取张家港市中部水系构建一维非稳态模型,中部水系主要的引水河道为朝东圩港和一干河,排水河道主要为二干河,9个水文自动监测站点位置如图1所示,实时输出频率为1 min的流量、水位和流速数据为模型边界条件、初始条件设置以及参数率定验证提供良好的数据支撑。
2 分析方法
时间尺度即流量的监测频率,研究基于朝东圩港老闸站流量自动监测数据,以0.5 h、1 h、2 h、3 h、4 h、5 h、6 h、12 h、24 h为时间尺度,选取不同开始取值时刻,得到多组模型边界入流序列。采用相对误差、决定系数和纳什效率系数描述模型水动力(流量、水位)和水质(COD、氨氮)模拟精度,用3个指标的变化曲线来评价影响程度。
一般认为,相对误差在[-20%,20%]以内,决定系数大于0.6,模拟效果可接受[14];纳什效率系数在(0.75,1]之间表示模拟效果非常好,在(0.65,0.75]之间表示模拟效果较好,在(0.50,0.65]之间表示模拟效果一般,在(-∞,0.5]之间表示模拟效果不好[15]。相对误差越小、决定系数和纳什效率系数越大,表明模拟精度越高。
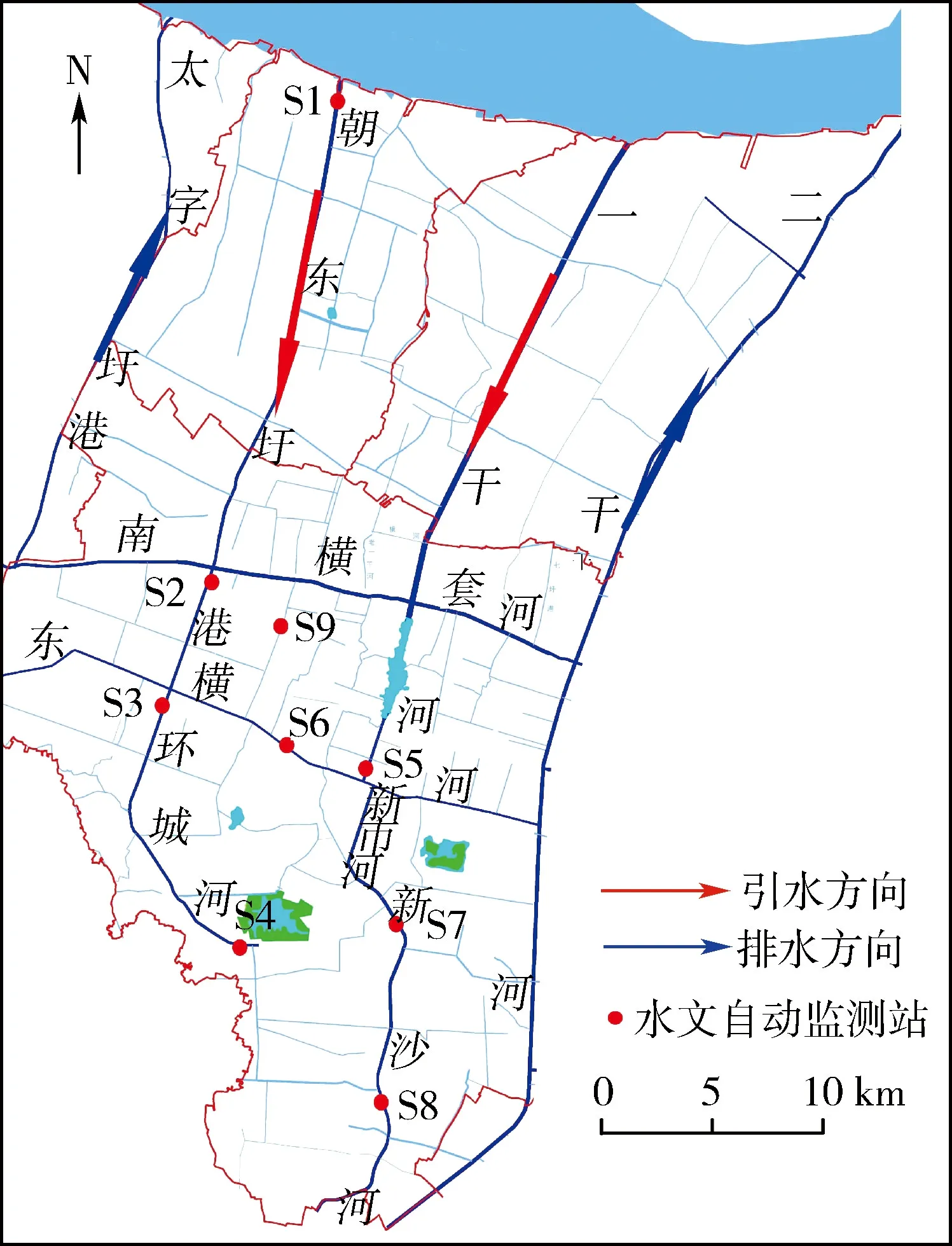
图1 张家港市水循环体系及中部水系水文自动监测站分布
3 模型构建与率定
基于野外同步监测数据、自动高频监测数据、常规监测资料构建张家港市中部水系一维非稳态水动力水质模型,水动力模型计算采用圣维南方程组[16-18],主要依据动量守恒和质量守恒原理,以水位和流量为未知变量,同时考虑了旁侧入流和漫滩的影响,水质模型计算采用污染物对流扩散方程[19]。
根据概化后河网、湖泊在输水能力和调蓄能力与实际河网、湖泊相近或基本一致的原则[20],将张家港市镇级以上河道、沿江水利枢纽、内河节制闸进行概化,共概化得到368条河流、151个闸站。中部水系朝东圩港、一干河与长江交汇处的进水口为模型上边界,根据沿江水文监测站监测数据确定流量边界,太字圩港、二干河与长江交汇处为模型下边界,根据同步监测数据确定水位边界;水质数据参考张家港市水功能区常规断面监测数据确定,模型初始水位的设定参考同步监测数据及往年水文资料,设置常水位为3.69 m。
于2016年1月11—12日在张家港市中部水系开展野外水动力水质同步监测,布设5个水文监测断面,采用流速仪人工测量流速,水尺、自动水位计测量水位,监测频率为开闸引水后每0.5 h或1 h;布设17个水质监测断面,采集水样送实验室分析,监测频率为开闸前采集一次水样用于本地浓度值测定,开闸后主要断面每1 h采集水样。
同步监测数据结合水文站实时监测数据用于模型率定,结果显示:张家港市现状河道糙率为 0.01~0.04,COD降解系数为0.04~0.08 d-1,氨氮降解系数为0.03~0.08 d-1;流量率定结果相对误差均值在20%以内,水位率定结果误差在10 cm以内,水质率定结果相对误差在30%以内,表明该水动力水质模型模拟效果良好,可用于后续模拟计算。
4 模拟结果与分析
4.1 不同时间尺度边界入流特性及代表性
平原感潮河网地区大多利用潮汐与内河水位差控制闸门启闭,引水流量变化与潮位变化具有相同的周期性。长江潮位和张家港朝东圩港水利枢纽内河水位、流量情况如图2所示,长江潮位基本高于朝东圩港水利枢纽内河水位,满足引水条件;朝东圩港实测流量与潮位变化一致,流量变幅受潮汐影响较大,最大流量可达180 m3/s左右。

图2 长江潮位、朝东圩港水位与流量变化
基于朝东圩港2016年2月6日引调水流量数据,以零点为开始取值时刻,以不同时间尺度筛选入流边界序列进行数据代表性分析。图3(a)为全天时段入流序列曲线,理论上时间尺度越小越易取到更多数据,更具代表性,但时间尺度小于3 h和为5 h时有流量峰,而时间尺度为4 h和大于6 h时无流量峰,说明是否有流量峰不仅与时间尺度有关,还与开始取值时刻相关;图3(b)为引水时段入流序列曲线,时间尺度为0.5 h时,边界入流流量序列取到原始流量峰数据上3个数据点,1 h时为2个数据点,2 h、3 h和5 h时为1个数据点,时间尺度增大导致取到原始流量峰数据上数据点变少,对引水时段流量曲线的还原变差。由表1可知总水量误差、相关系数以及流量峰值大小并不随时间尺度变化呈规律性变化,时间尺度小于2 h时,随着时间尺度的增大总水量误差增大,相关系数减小,流量峰值减小;时间尺度大于2 h时,总水量误差、相关系数、流量峰值变化无明显规律;时间尺度小于1 h时,不论是在引水和非引水全天时段或单独引水时段,总水量误差小于20%,相关系数大于0.9,表明该时间尺度边界入流数据具有代表性,能够较为准确描述实际情况。
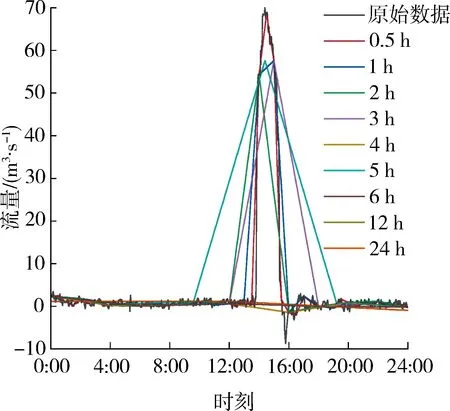
(a) 全天时段

(b) 引水时段
基于朝东圩港2016年2月6日引调水流量数据,选取较小时间尺度0.5 h及较大时间尺度3 h,进一步分析全天时段和引水时段开始取值时刻不同对边界入流的影响。时间尺度为0.5 h时,全天时段开始取值时刻分别为0:00、0:05、0:10、0:15、0:20、0:25、0:30、0:40、0:50、1:00、1:10,得到11组流量序列,如图4(a)所示;引水时段从下午13:45开始,14:23达到峰值,持续时间约2 h,从13:45每间隔 5 min 或10 min开始取值得到11组流量序列,如图4(b)所示,前7组数据为流量峰曲线到达峰值前开始取值,后4组为曲线到达峰值后开始取值。由表2可知,全天时段总水量误差最大为5.2%,流量峰值误差在10%以内,说明时间尺度较小时开始取值时刻不同对边界入流代表性影响较小;引水时段总水量误差在9.0%~58.0%之间,流量峰值误差在0.8%~13.0%,流量峰值前开始取值组别总水量和流量峰值的误差小于流量峰值后开始取值组别,开始取值时刻不同造成的误差主要体现在引水时段。时间尺度为3 h时,研究从零点每间隔15 min开始取值得到12组流量序列,如图5(a)所示;从开始引水时刻13:45开始每间隔10 min取值,得到12组流量序列,如图5(b)所示,前4组数据为流量峰曲线到达峰值前开始取值,后8组为曲线到达峰值后开始取值。由表3可知,全天时段总水量误差在34.0%~99.0%之间,流量峰值误差在2.0%~100.0%之间;引水时段总水量误差在26.0%~94.0%之间,流量峰值误差在1.0%~98.0%之间,时间尺度较大时取值开始时刻越靠近流量峰值误差越小。
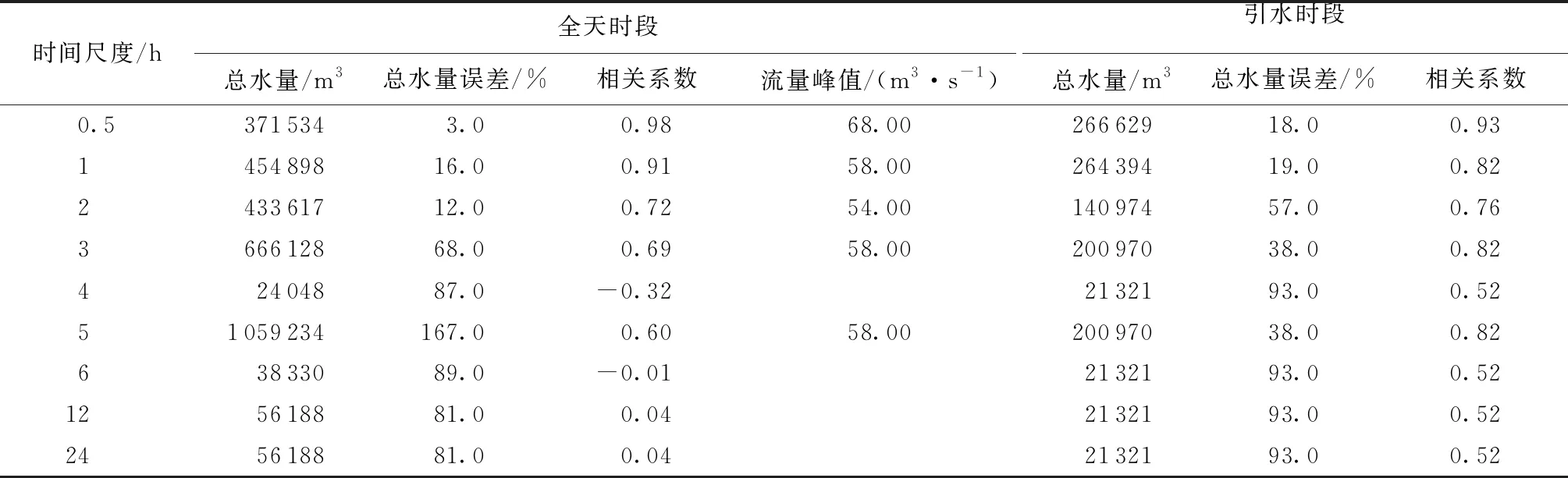
表1 不同时间尺度边界入流总水量及曲线相关系数

(a) 全天时段

(b) 引水时段
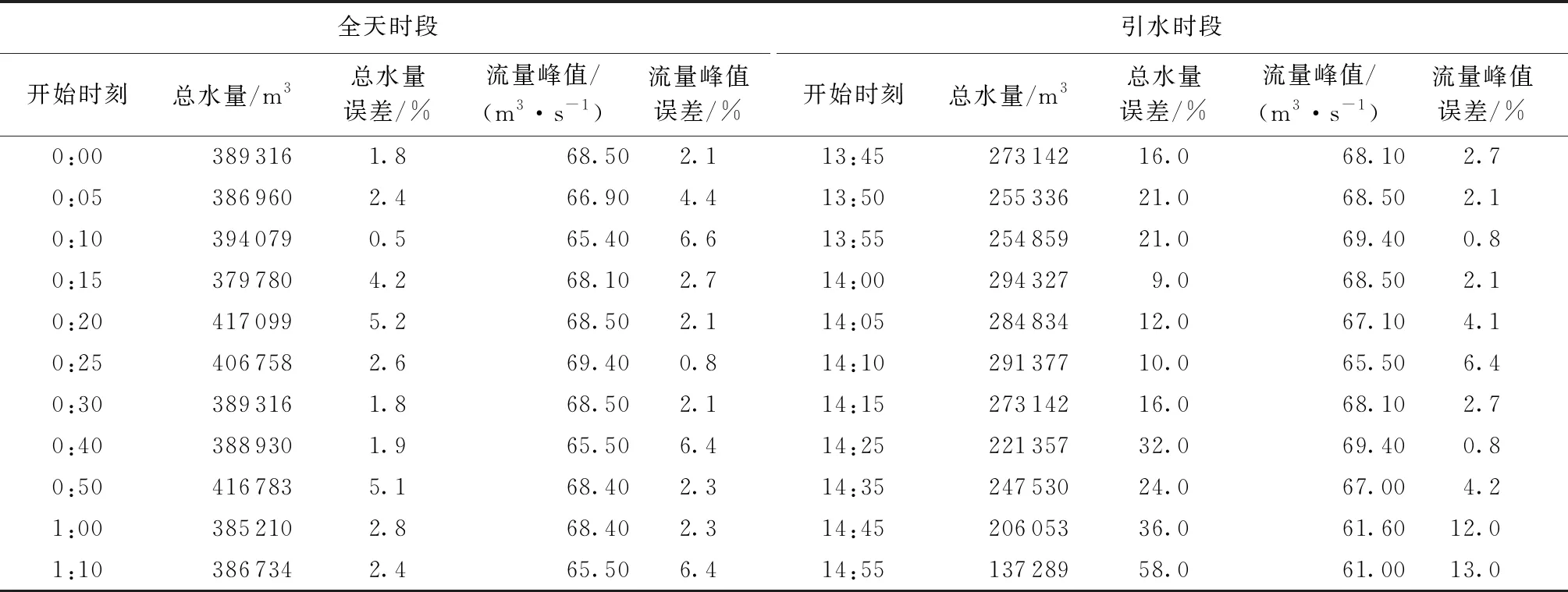
表2 0.5 h时间尺度不同开始取值时刻总水量和流量峰值误差

(a) 全天时段
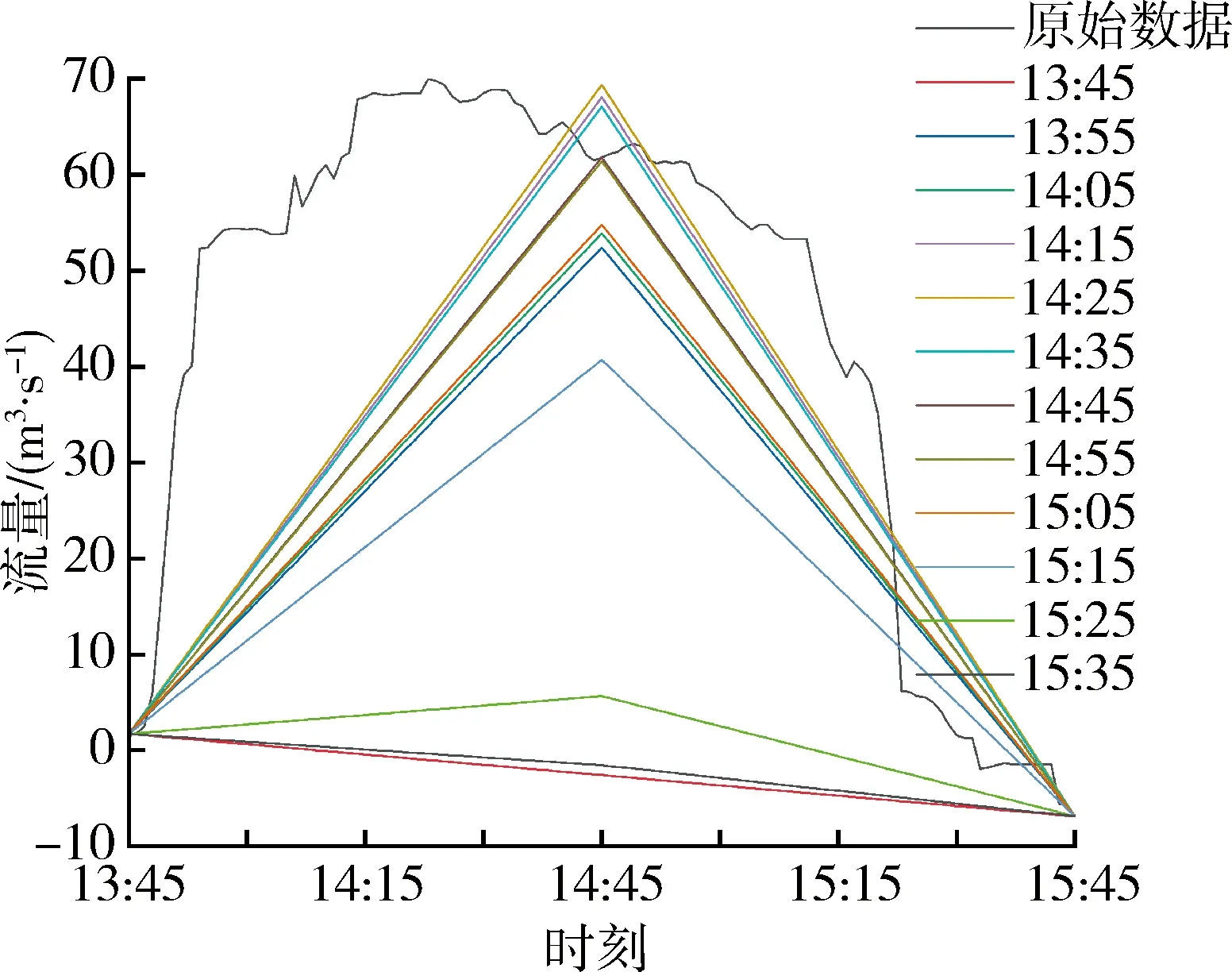
(b) 引水时段
表3 3 h时间尺度不同开始取值时刻总水量和流量峰值误差
Table 3 Deviation of the total water volume and peak flow at different starting time of whole day and diversion period in 3 h time scale
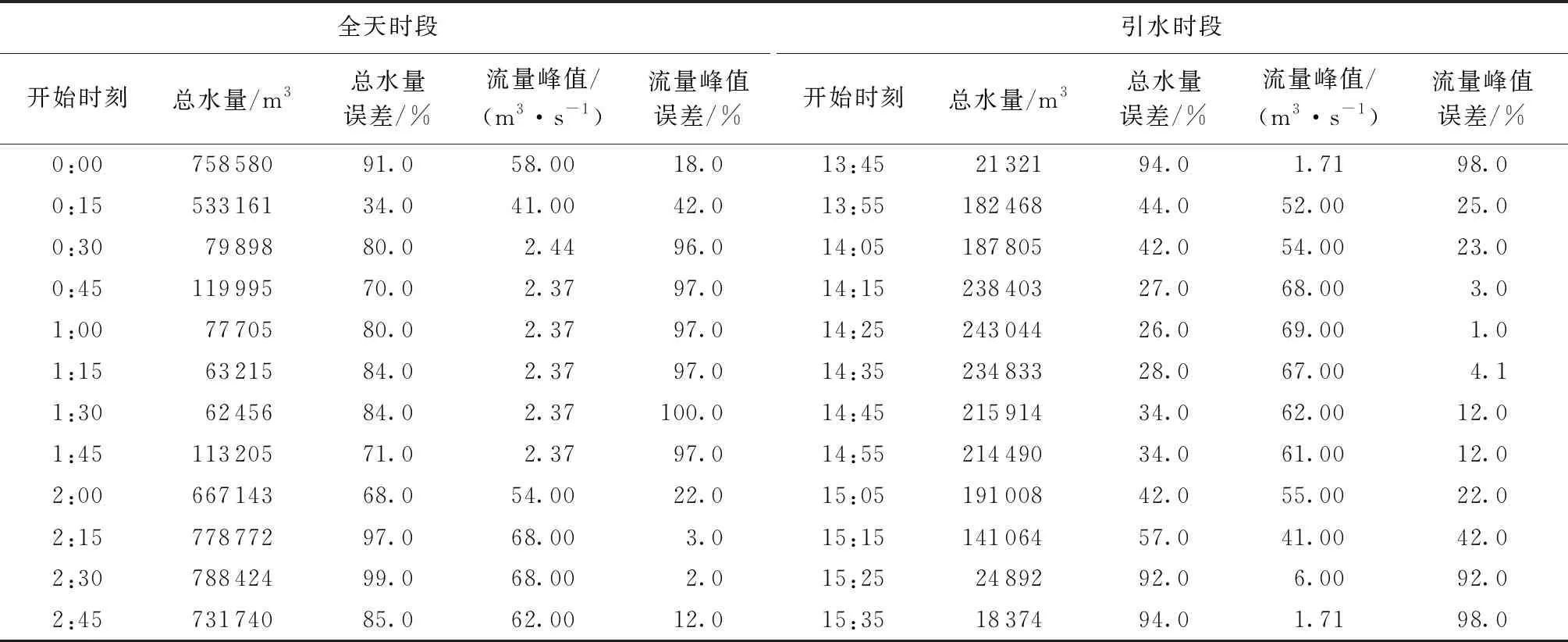
全天时段引水时段开始时刻总水量/m3总水量误差/%流量峰值/(m3·s-1)流量峰值误差/%开始时刻总水量/m3总水量误差/%流量峰值/(m3·s-1)流量峰值误差/%0:0075858091.058.0018.013:452132194.01.7198.00:1553316134.041.0042.013:5518246844.052.0025.00:307989880.02.4496.014:0518780542.054.0023.00:4511999570.02.3797.014:1523840327.068.003.01:007770580.02.3797.014:2524304426.069.001.01:156321584.02.3797.014:3523483328.067.004.11:306245684.02.37100.014:4521591434.062.0012.01:4511320571.02.3797.014:5521449034.061.0012.02:0066714368.054.0022.015:0519100842.055.0022.02:1577877297.068.003.015:1514106457.041.0042.02:3078842499.068.002.015:252489292.06.0092.02:4573174085.062.0012.015:351837494.01.7198.0
从误差变化区间分析可知,当时间尺度较大时,开始取值时刻对全天和引水时段流量序列影响较为明显,可能是当时间尺度大于引水时间时,在引水时段内最多只能取到原始流量数据序列上的1个数据点,故需保证尽量取到流量峰值附近的数据点以减小误差。开始取值时刻对边界入流条件代表性的影响程度随时间尺度的增大而变大,在实际监测过程中,未知引调水开始时刻情况下应尽量选取较小的时间尺度进行监测;已知引调水开始时刻情况下可以在非引调水过程选取较大时间尺度测量少量数据点,引调水过程中减小时间尺度、增大取样频率并保证流量峰值附近采集到较多的数据点。
基于朝东圩港2016年2月6—15日的引调水数据,综合比较9个不同时间尺度、12个开始取值时刻边界入流代表性。总水量比值、相关系数、流量峰数量和峰值情况见表4,总水量比值和相关系数变化趋势见图6,随时间尺度增大,总水量比值均值增大,相关系数均值减小,说明边界入流代表性变差,变化区间增大说明开始取值时刻不同造成的影响增大。时间尺度小于1 h时,流量峰为9个,可较为准确地反映引水次数,不受开始取值时刻的影响;时间尺度大于2 h时,峰数量明显减少;时间尺度为24 h时,流量序列失去流量峰,失真严重。流量峰值波动随着时间尺度的增大而增大,时间尺度小于1 h时,总水量比值上下边界误差小于5%,相关系数大于0.9,峰数量为9个,流量峰值变化幅度在10%以内,说明此边界条件可信。该时间尺度小于张家港引水时间,可能是由于较小的时间尺度能够大概率地覆盖引水数据,时间尺度过大容易错过或取到少量引水数据点,导致模型边界入流失真,影响模拟精度。平原感潮河网地区进行水文野外同步监测时需关心相关地区的潮位情况、引调水开始时刻,选取合适的时间尺度。

表4 不同时间尺度边界入流流量序列特征值

(a) 总水量比值
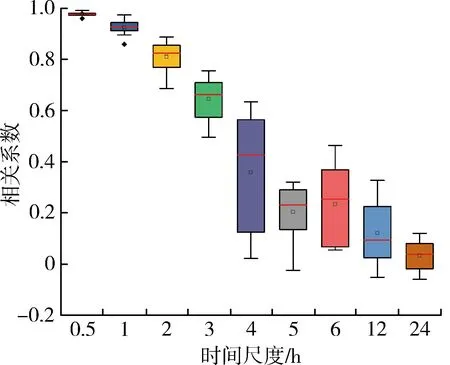
(b) 流量序列相关性
4.2 不同时间尺度边界入流条件对水动力模拟精度的影响
水动力模拟结果的相对误差、决定系数和纳什效率系数变化情况如图7所示。由图7(a)可知,流量的相对误差随时间尺度增大而增大,时间尺度小于4 h时小于20%,模拟精度较高,时间尺度为24 h时增大到600%,曲线在时间尺度大于6 h时上升幅度变大表明时间尺度对模拟精度影响变大;水位的相对误差几乎不受时间尺度变化影响,一直维持在0.15%~1.78%之间,误差在10 cm以内,模拟精度较高。由图7(b)可知,流量的决定系数随时间尺度增大而减小,时间尺度小于1 h时大于0.6,模拟精度较高,时间尺度为24 h时下降到0.01,曲线在时间尺度大于6 h时下降幅度变小表明时间尺度对模拟精度影响变小;水位的决定系数在时间尺度小于2 h时大于0.6,模拟精度较高,时间尺度为24 h时降低到0.01,其曲线变化趋势与流量的决定系数相近,时间尺度变化对模拟精度影响由大变小。由图7(c)可知,流量的纳什效率系数随时间尺度增大而减小,时间尺度小于1 h时大于0.65,模拟精度较高,时间尺度为24 h时下降到-6.86,曲线在时间尺度大于1 h时下降幅度变大表明时间尺度对模拟精度的影响变大;水位的纳什效率系数在时间尺度小于2 h时大于0.65,模拟精度较高,时间尺度为 24 h 时降低到-61.23,其曲线变化趋势与流量的纳什效率系数相近,时间尺度变化对模拟精度影响由小变大。
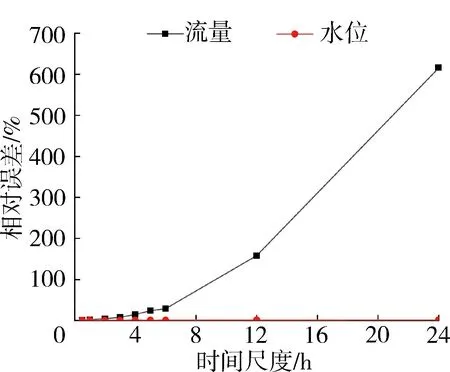
(a) 相对误差
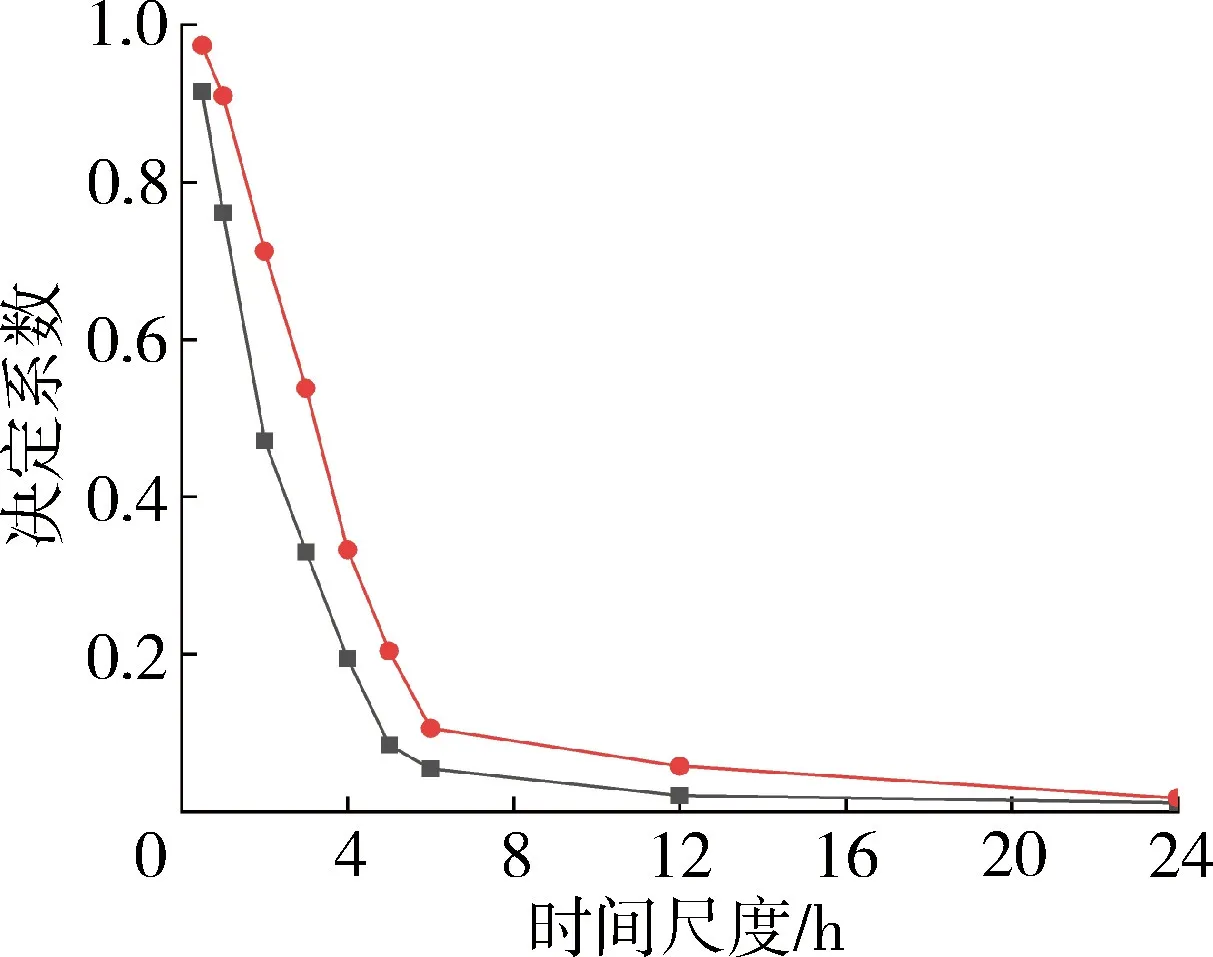
(b) 决定系数

(c) 纳什效率系数
各项指标变化曲线在6 h左右发生突变可能与朝东圩港边界入流条件在该时间尺度下流量峰数量迅速减少有关;时间尺度小于1 h时流量、水位模拟结果相对误差在[-20%,20%]以内,决定系数大于0.6,纳什效率系数大于0.6,模拟精度较高,故研究区域水动力模拟结果可信的最大时间尺度为1 h;其中水位的相对误差小于流量,水位的决定系数、纳什效率系数大于流量的决定系数和纳什效率,水位模拟精度优于流量模拟精度。
4.3 不同时间尺度边界入流条件对水质模拟精度的影响
水质模拟结果的相对误差、决定系数和纳什效率系数变化情况如图8所示。由图8(a)可知,COD的相对误差随着时间尺度增大一直小于20%,模拟精度较好;氨氮的相对误差随时间尺度增大而增大,时间尺度小于6 h时小于20%,模拟精度较高,时间尺度为24 h时增大到27.2%,曲线在时间尺度大于6 h时上升幅度变小表明时间尺度对模拟精度影响变小,氨氮的曲线变化趋势与COD相近,时间尺度对模拟精度影响由大变小。由图8(b)可知,COD的决定系数随时间尺度增大而减小,时间尺度小于2 h时大于0.6,模拟精度较高,时间尺度为24 h时降低到0.30,曲线在时间尺度大于6 h时下降幅度变小表明时间尺度对模拟精度影响变小;氨氮的决定系数在时间尺度小于2 h时大于0.6,时间尺度为24 h时降低到0.33,变化趋势与COD相近,时间尺度变化对模拟精度影响由大变小。由图8(c)可知,COD的纳什效率系数随时间尺度增大而减小,时间尺度小于2 h时大于0.65,模拟精度较高,时间尺度为 24 h 时降低到-13.07,曲线在时间尺度大于4 h时下降幅度变大表明时间尺度对模拟精度影响变大;氨氮的纳什效率系数在时间尺度小于2 h时大于0.65,时间尺度为24 h时降低到-7.8,变化趋势与COD相近,时间尺度变化对模拟精度影响由小变大。
各项指标变化曲线在6 h左右发生突变可能与朝东圩港边界入流条件在该时间尺度下流量峰数量迅速减少有关;时间尺度小于2 h时,COD和氨氮模拟结果相对误差在[-20%,20%]以内,决定系数大于0.6,纳什效率系数大于0.6,模拟精度较高,故研究区域水质模拟结果可信的最大时间尺度为2 h;其中COD的相对误差、决定系数、纳什效率系数小于氨氮,氨氮模拟精度优于COD。当边界入流能够较好地模拟实际情况时,模型水动力水质模拟精度较高,总体水质相对误差小于水动力相对误差,水质的决定系数、纳什效率系数大于水动力的决定系数和纳什效率系数,水质模拟精度更高。综合来看张家港市平原感潮河网水动力水质模型可信的最大时间尺度为1 h。
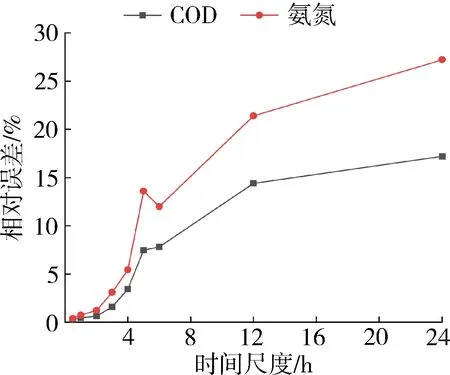
(a) 相对误差

(b) 决定系数

(c) 纳什效率系数
5 结 论
a. 平原感潮河网水动力水质模型边界入流受潮位控制,其代表性受时间尺度、开始取值时刻和调度情况影响,并非为单纯的线性关系,张家港市全天时段和引水时段边界入流条件可信的最大时间尺度为1 h。
b. 随着时间尺度的增大,模拟结果的相对误差增大,决定系数、纳什效率系数减小,张家港市感潮河网水动力、水质模拟可信的最大时间尺度为 1 h;水质模拟精度优于水动力模拟精度,水位模拟精度优于流量模拟精度,氨氮模拟精度优于COD模拟精度。
c. 平原感潮河网地区进行野外同步监测时,监测时间尺度的选取需关心潮位情况、引调水开始时刻及引调水周期,未知引调水开始时刻情况下选择较小时间尺度进行监测,已知引调水开始时刻情况下可在非引调水过程选取较大时间尺度测量少量数据,引调水过程中减小时间尺度、增大取样频率并保证采集到较多的数据点。
