基于回溯正则化的前向搜索正交匹配追踪算法研究
2020-05-21刘海鹏董士谦
陶 亮, 刘海鹏*, 王 蒙, 董士谦
(1.昆明理工大学 信息工程与自动化学院, 云南 昆明 650500;2.华能澜沧江水电股份有限公司, 云南 昆明 650200)
随着数字化的快速发展,我们正处在数字时代,身处这样时代的重要特征就是所有的信号采集都必须有相应的数字化软硬件支撑。然而,随着人们对信息量的大量需求,越来越需要更大的带宽来携带信息,传统的信号采样受限于奈奎斯特定理,采样速率低下,所以急需一种新的信号采样方法,在这种情况下压缩感知被提了出来。
压缩感知是由Donoho[1](美国科学院院士)、Candes等[2]提出来的一种革命性信息获取和处理方面的理论,带来了全新数据处理方式。压缩感知的主要原理是利用原始信号具有稀疏性或者在某个变换域中具有稀疏性,然后用一个观测矩阵对其进行观测降维,得到一个维度远小于原始信号但信息量却与原始信号基本等同的观测值,最后再将原始信号从观测值恢复出来的一个过程。有效的解决了奈奎斯特[3]采样存在的不足,减少了存储和计算资源。
目前关于压缩感知的研究主要是如何精确的将原始信号从观测值中恢复出来,即信号的重构,在信号重构各类方法中,贪婪算法由于其耗时短、过程简单而受到高度关注。例如匹配追踪(Matching Pursuit,MP)、正交匹配追踪[4](Orthogonal Matching Pursuit,OMP)、前向搜索正交匹配追踪(Look Ahead Orthogonal Matching Pursuit,LAOMP)算法等等。
但是上述算法重构精度仍然不够精确,其中OMP算法是在MP算法基础上改进的,而LAOMP算法是在OMP算法上改进的,LAOMP算法目前得到较为广泛的应用,但是LAOMP算法采用前向搜索策略(Look Ahead Residual,LAR)得到的原子不一定就是最优的原子,即重构精度存在不足。因此,本文在LAOMP算法的基础上加以改进,提出了一种回溯正则化前向搜索正交匹配追踪(Backtracking Regularized Look Ahead Orthogonal Matching Pursuit,BRLAOMP)算法。该算法在LAOMP算法选择原子的基础上,又加入了回溯策略和正则化来挑选原子,使选择出来用以重构的原子能达到最佳,所以该算法的重构精度与同类算法相比明显得到提高。
1 算法描述
1.1 LAOMP算法
OMP算法作为最早的贪婪迭代算法之一,其思想对之后的各种贪婪算法有着极其重要的意义,它沿用了MP算法中的原子选择准则。OMP算法以贪婪的方式选择原子(通常将感知矩阵中的每一列称为原子),在每次迭代中,找出感知矩阵中的每一列向量与残差,相乘得到最大内积值对应的原子,并在其中找到该原子所对应的索引值进行存储;然后更新原子集,更新残差;最后判断是否满足迭代停止条件,进而输出估计信号。但是OMP算法在每次进行原子选择的时候选择的原子未必是最优的,而且每次迭代中仅仅选择一个原子来更新,也将消耗很多时间。于是Saket Chatterjee等[5-7]在OMP算法的基础上提出了LAOMP算法。
LAOMP算法作为一种应用较为普遍的压缩感知重构算法,与OMP算法相比,主要采用了前向搜索策略。该算法在选择原子的过程中,通过判断所选原子对未来迭代的影响来选择最佳的原子。该算法的原理是首先选择出若干最大内积所对应的原子,并将这个原子所对应的索引存储起来,然后逐次迭代,比较这些原子对最终残差的影响,最终选择残差中二范数最小的一个原子所对应的索引加入到支撑集中,然后更新原子集,更新残差,判断是否满足终止条件,输出近似信号,以达到对原信号的重构。
LAOMP算法的核心是LAR算法,具体描述如下:
输入:传感矩阵AM×N,观测向量YM×N,稀疏度k,先前支撑集Ipre,新选择的原子索引t。
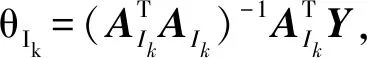
迭代过程:
1)迭代次数k=1∶L;
3)更新支撑集Ik=Ipre∪tk;
5)更新残差rk=Y-AIkθIk;
6)判断是否满足迭代停止条件‖rk‖2>‖rk-1‖,若满足,则停止迭代,否则,重复步骤1—6。
输出:rk=Y-AIkθIk。
对于给定的稀疏度k,候选原子索引集Ipre,原子索引t,LAR算法最后得到K个元素候选集并返回最后的残差,LAR算法可以定义LAR函数如下:
r=LAR(Y,A,k,Ipre,t)。
(1)
1.2 BRLAOMP算法
LAOMP算法虽然相对于OMP算法能更好地选出迭代需要的原子,但是,OMP算法、LAOMP算法等,在每一次迭代的时候都是寻找传感矩阵中的每一列与残差相乘的最大内积值所对应的原子,称之为最佳原子,但是由于数据的随机不确定性以及运算中可能出现的复数,导致所选择的最大内积值未必就是最大的值,所以最终通过前向搜索策略(LAR)得出的原子不一定就是最优的原子,鉴于此,本文提出了BRLAOMP算法,该算法在LAOMP算法的基础上增强了挑选原子的力度。BRLAOMP算法首先通过残差相乘的方式选择内积最大的前2L个原子,接着用最小二乘法求出这些原子的稀疏表示系数估计θ,去除L个系数估计θ数值较小的原子,即用回退筛选[8-9]的思想选择保留L系数较大的原子。然后对这L个原子进行正则化[10-11],选出能量最大的原子集,最后将这些能量最大的原子加入到LAR中,选择残差性能最佳的原子,更新支撑集,更新残差,直至满足终止条件并输出结果。
BRLAOMP算法的核心是由回溯策略、正则化和LAR算法3个部分组成。LAR算法已经介绍了,接下来介绍回溯策略和正则化算法。
1.2.1 回溯策略
回溯策略也就是回退筛选,其基本思想是从一条路往前走,能进则进,不能进就退回来。本文对它的基本操作是先选出2L个内积值最大的原子,然后直接用最小二乘法求出每个原子稀疏表示系数估计θ,对这2L个系数进行降序排列,选出前L个系数最大的原子对应的索引。就可以把一些内积值较大却并非是最佳原子的原子去掉。这样经过回退筛选得到的原子拥有更好的重构精度。具体操作如下:
1)初始余量r0=Y,索引值集合Ω=∅,J=∅;支撑集P=∅;
2)用公式u={uj=|
3)令Ω=Ω∩J,用θ=(ΩTΩ)-1ΩTY求得信号逼近系数θ,取前L个最大系数的原子放入支撑集P中,等待下一步操作。
1.2.2 正则化算法
正则化是从支撑集P中寻找符合|u(i)|<2|u(j)|的原子,其中u指的是各原子与残差的内积值,正则化过程能够在一个原子集中筛选出能量较大的原子,是一种简单有效的原子筛选方法,这样筛选出来的原子一定程度上提高了重构精度。正则化算法过程如下:
输入:回退筛选得到的支撑集P。
初始化:初始化最大能量值Emax=0,自变量t=1。
迭代过程:
1)将支撑集P中L个原子对应的索引值存入J中;
2)计算P中的原子与余量的内积值存入Jval中;
3)外部循环次数k=1∶L
①存储本次寻找的最佳索引值Jpos(t)=J(k);
②存储本次寻找的能量最大值En=Jval(k)2;
③内部循环次数m=(k+1)∶L
a)寻找符合条件|u(i)|<2|u(j)|的内积值Jval(k)<2×Jval(m);
b)自变量更新t=t+1;
c)索引值Jpos(t)=J(m);
d)能量更新En=En+Jval(k)2;
如果不满足条件,结束内部循环。
5)如果最大能量值En>Emax;
6)更新索引值Jt=Jpos(1∶t);
7)更新能量值Emax=En。
输出:索引值pos=Jt,能量值val=Emax。
定义正则化过程公式:
[Val,pos]=Re(P,L)。
(2)
1.2.3BRLAOMP算法具体步骤
输入:传感矩阵AM×N,观测矩阵YM×N。
初始化:近似系数θ=0,初始残差r0=Y,支撑集I=∅,pos_theta=[];索引值集合Ω=∅,J=∅;支撑集P=∅。
迭代过程:
1)外部循环次数k=1∶M;
2)计算A的各列与残差的内积u=ATrk-1;
3)对内积做降序排列,取前2L个内积最大的原子对应的索引放入J中;
4)令Ω=Ω∪J,θ=(ΩTΩ)-1ΩTY求得信号逼近系数θ,对θ降序排列,取前L个最大系数的原子放入支撑集P中;
5)正则化[Val,pos]=Re(P,L);
6)内部循环次数l=1∶L;
a)由LAR得到残差值r=LAR(Y,A,k,Ipye,t);
b)存储残差nl=‖r‖2;
c)选择残差值的二范数最小的原子对应的索引值ik;
7)更新支撑集Ik=Ik-1∪ik;
9)存储支撑集pos_theta=Ik;
10)判断是否满足迭代终止条件‖rk‖2>‖rk-1‖。
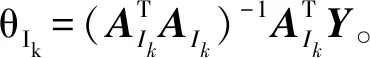
2 仿真结果和分析
验证本文提出的回溯正则化前向搜索正交匹配追踪(BRLAOMP)算法实现信号的高精度重构,以下仿真结果是在MATLAB R2014a环境下进行。
2.1 一维信号重构实验
2.1.1 一维信号高精度重构
先用一维重构实验来测试本算法是否可以精确地将原始信号从观测值中恢复出来,实验结果如图1所示,其中横坐标表示信号的维数,图中有12条黑线表示原始信号,12个黑点表示恢复出来的信号,12是设置的稀疏度,从图中可以看出黑点与黑线高度重合,表示信号被完整地恢复出来。
2.1.2 BRLAOMP算法稳定性验证
测试本算法在不同稀疏度下的恢复情况,当恢复残差小于10-16时认定重构成功,计算出不同稀疏度一维信号重构的概率,实验结果如图2所示,其中横坐标表示测量数,纵坐标表示重构率。重构率达到100表示恢复成功,从图中可以看出,测量数在150左右时,所有不同稀疏度的信号全部成功恢复。
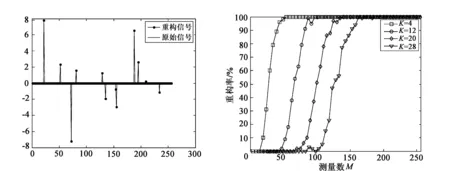
图1 一维信号的重构实验 图2 一维信号准确重构概率
2.2 二维信号重构实验
2.2.1 3种算法重构实验对比
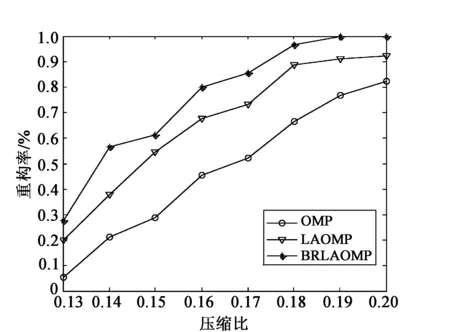
图3 在高斯信号下的ERP对比图
对OMP算法、LAOMP算法、BRLAOMP算法进行精确重构率(ERP)对比实验,在不考虑噪声的情况下,稀疏基矩阵选择小波变换正交基,观测矩阵[12-18]选择高斯随机矩阵[19-20]。仿真参数设置如下:令原信号X分别为长度700的高斯随机信号和长度为1000的二值信号,稀疏度K设置为25。原信号为高斯随机信号,压缩比区段设置为[0.13,0.2],共8个点,测量次数为90次。结果如图3所示,可以看出随着压缩比的增大,3种算法的ERP均增大,但本算法的增大效果更明显。其中在压缩比相同的情况下,本算法ERP要比另外两种算法效果好,能在较低的压缩比下也能达到满意的效果,当压缩比达到0.19时重构率(ERP)就趋近1,即趋近于完全重构。而另外两种算法的重构率分别为0.8、0.9。由此可见本算法的优越性。
2.2.2 二维图像重构实验比较
以图像的峰值信噪比(PSNR)和相对误差(RE)作为图像恢复质量的评判依据,压缩比M/N分别选取0.3、0.5、0.7。其中稀疏基矩阵采用小波变换矩阵,测量矩阵采用高斯随机矩阵。仿真结果如图4、图5、图6所示,可以看出,对于同一幅二维图片,在压缩比分别为0.3、0.5、0.7中,压缩比为0.3的图片最模糊,而压缩比为0.7最为清晰,压缩比为0.5的清晰度介于二者之间,但在压缩比相同的情况下,本文提出的BRLAOMP算法重构的图像均比另外两种算法重构得到的图片清晰。

图4 压缩比为0.3的二维图像重构实验
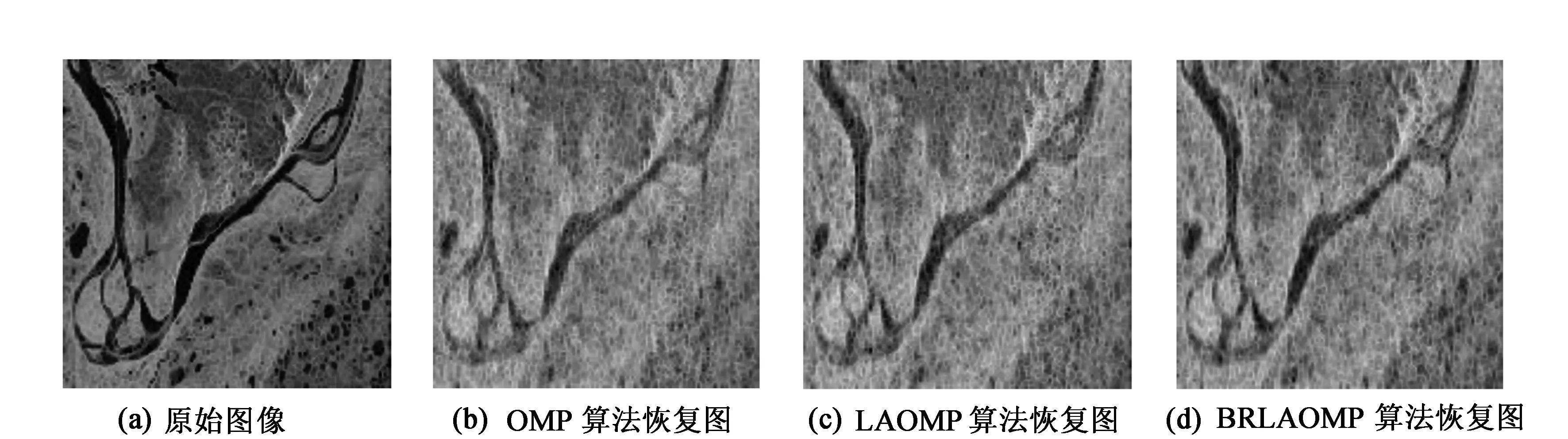
图5 压缩比为0.5的二维图像重构实验
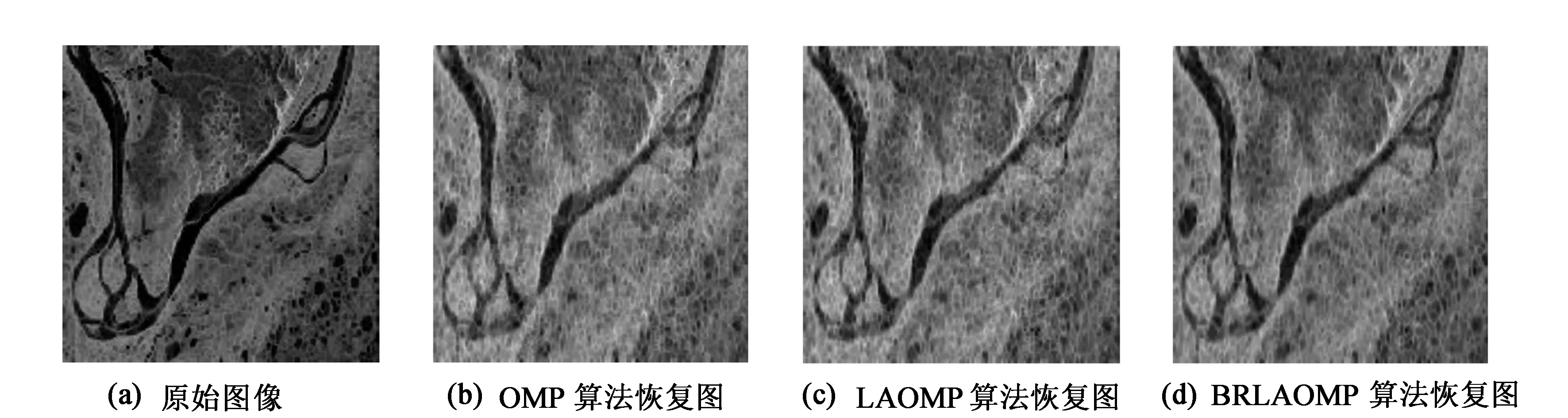
图6 压缩比为0.7的二维图像重构实验
2.2.3 二维图像重构质量比较
当压缩比相同时,BRLAOMP算法的峰值信噪比(PSNR)最大,而相对误差(RE)最小,见表1。说明BRLAOMP算法重构质量优于另外两种算法,且随着压缩比的增大,各算法的PSNR均增大,而RE均减小,但BRLAOMP算法效果最为明显,其PSNR均大于其他算法,RE均小于其他算法,可见该算法的优越性。
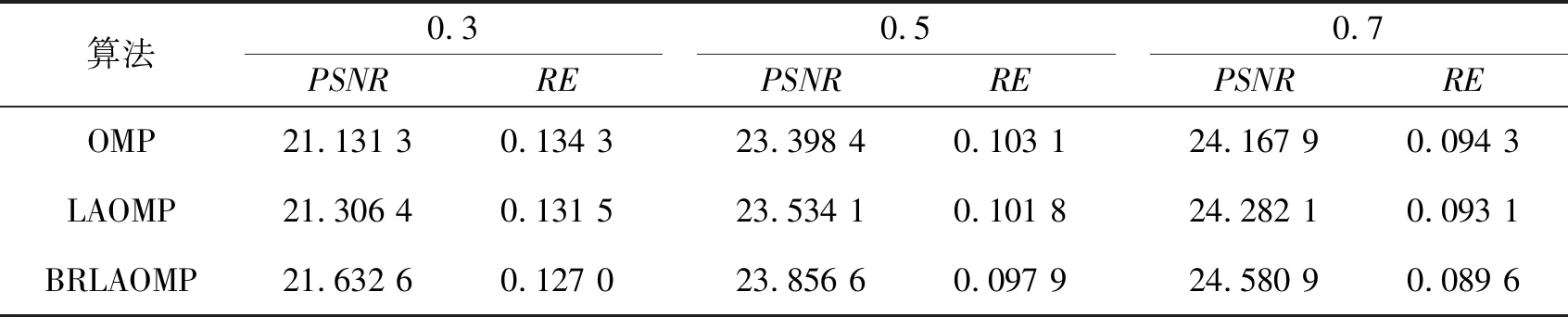
表1 压缩比为0.3、0.5、0.7时二维图像重构质量比较
3 结论及讨论
本文在LAOMP算法的基础上引入了回溯思想和正则化算法,强化了对原子的选择,提出了一种改进的前向搜索正交匹配追踪(BRLAOMP)算法。经过仿真对比,发现该算法的重构质量明显优于LAOMP算法。但在运行时间上,BRLAOMP算法比较长。如在一维信号重构实验中,OMP算法重构时间约为0.06 s,LAOMP算法的重构时间为0.19 s,BRLAOMP算法的重构时间约为0.29 s,这是由于本算法用了3种方式来筛选原子,故在重构时间上表现出劣势,后续将针对算法运行时间方面做进一步研究。
