共轴双柱式波能装置水动力及能量转换特性研究

张万超,王逸生,周效国*,周亚辉

(1.江苏科技大学 船舶与海洋工程学院, 镇江 212003) (2.江苏科技大学 能源与动力学院, 镇江 212003) (3.江苏科技大学 海洋装备研究院, 镇江 212003)

随着全球对能源和电力需求的逐步增加[1-4],自二十世纪末,从海洋中获取能量成为替代能源的主要方式.海浪作为一种持续的海洋能,通过数值理论或实验研究,安全范围内提高其转换效率受到越来越多的关注．目前,通过不同运动模态和动力输出系统形式的单浮体式俘获波能装置已被广泛研究,而如何将其运用于深水并高效地获取能量成为研究热点．为此,基于现有的单浮体装置,通过设置不同形式载体,进而构成双体式波能装置并将其运用于深水成为主要的手段,而作为直驱的点吸式波浪能转换装置,其深水中设置载体对系统波浪能转换能力的影响研究,对其他波能转换形式的相关研究具有重要借鉴意义．

阻尼板作为海洋工程领域常用的辅助性构件,通常用于提升装置稳定性[5-7],而将其运用于波浪能装置只有部分研究[8-13],但大多仅将其视作悬浮在水中固定不动的反应板,忽略了阻尼板与漂浮浮子之间的相互水动力作用．事实上,阻尼板存在不仅改变浮体周围流场的水动力边界条件[14],其自身运动还会作用于浮子,浮子与阻尼板的相互作用会极大地影响系统的波能转换特性[15]．为此,针对考虑阻尼板的双浮体波能转换系统,文中基于线性微幅波假设,通过特征函数展开和边界匹配的势流半解析方法,得到了同轴双浮体的相互作用水动力特性;结合多自由度振动理论,探究了不同半径及浸没深度阻尼板条件下,装置在线性PTO系统作用下的能量转换效率,为后续振荡浮子式波浪能发电装置优化提供依据．

1 理论分析

1.1 波能转换模型

假定浮体通过动力输出系统(Power Take-off，PTO)与浮式平台连接,在波浪作用下作相对往复垂荡运动,激活阻尼器进而对外做功,由此构成一个复杂的双自由度振动系统,其振动模型如图1,其中ch和kh分别表示由水动力产生的等效阻尼和刚度系数,cp为PTO阻尼系数．

假定该系统在静水中处于静平衡状态,在线性波作用下,将振子瞬时位置与平衡位置的相对位移定义为其位移,同时假定入射波浪是线性微幅波．根据牛顿第二定律,波浪作用下该双体振动系统的受迫运动方程可以表示为：

(1)

图1 波能转换振动模型Fig.1 Oscillating model for the WEC

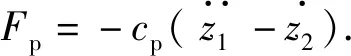
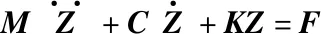
(2)

M=[aij],C=[bij],K=[cij],

Z={z1,z2}T,F={Fe1,Fe2}T,

(3)

(4)

求解上述线性方程组,得到浮子与载体的运动位移,结合阻尼器对外做功方式,可得由于浮子相对载体运动激励阻尼器对外做的功,具体可以表示为：

(5)

式中：

det[N(iω)]=N11N22-N12N21=(a+ib)cp+c+id

(6)

则波能俘获功率可以表示为:

(7)

式中：R表示取复数实部,由于(N22+N12)F1-(N11+N21)F2与PTO系统参数(阻尼系数)没有关系,因此当波浪能俘获功率对阻尼系数的导数为0时,得到的阻尼系数及对应的俘获功率即为最优的,具体表示为：

(8)

1.2 水动力模型

文中波能装置工作水域深度为h,获能结构为半径为R1,吃水为d1的漂浮圆柱形浮子,载体为与浮子共轴的浸没于浮子下方的阻尼圆盘,定义其半径为R2,浸水深度为d2,厚度为t．装置中PTO系统安装在立柱内部,连接浮子于阻尼板,不会对系统水动力产生影响,由此可以得到流域划分(图2)．在柱坐标系(r,θ,z)下,为便于描述波能装置在波浪中的流场特性,定义水平面rOθ在静水面上,Oz轴垂直向上．

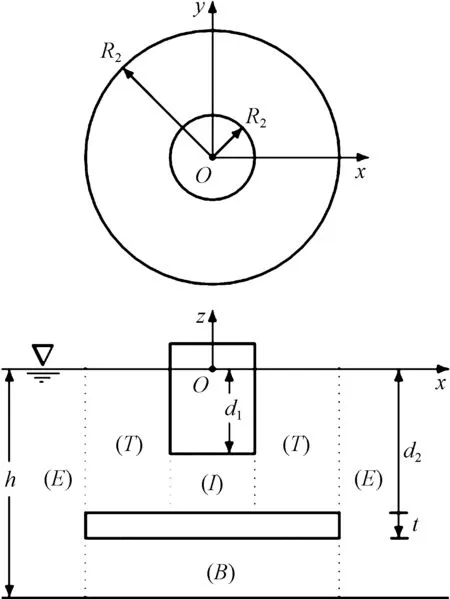
图2 双浮体模型及流域划分Fig.2 Sketch of the dual buoy and the definition of fluid subdomains

根据线性波理论,流域中的速度势可以提出其时间因子e-iωt,由此得到的空间速度势Φ(r,θ,z)可以分解为入射势、绕射势和辐射势,具体可以表示为：

Φ(r,θ,z)=Φ0(r,θ,z)+Φ7(r,θ,z)+

(9)

式中：Φ0(r,θ,z)为入射波的速度势；Φ7(r,θ,z)为散射速度势,它们共同组成绕射速度势ΦD(r,θ,z)；ξp,j表示浮体p做j模态的运动振幅,Φp,j(r,θ,z)表示由该模态运动产生的辐射速度势,由于本文仅考虑垂荡运动,则速度势Φp,j(r,θ,z)和位移幅值ξp,j可以分别用Φp(r,θ,z)和ξp代替．上述空间速度势需要满足域内Laplace方程、自由面条件、海底不可穿透条件及远场辐射条件,具体可以表示为:

2Φ=0
ω2Φ-g∂zΦ=0z=0,r≥R1
∂zΦ=0z=-h

(10)

此外,速度势还需要满足物面条件:

∂nqΦp=δpqnq, ∂npΦD=0

(11)

式中：下标p,q(p,q=1,2)为浮体编号；δpq为克罗内克符号．设入射波波幅为ξ0,沿x轴正向传播可表示为：

(12)

(13)

式中：k0为波数；ε1为诺伊曼的符号；g为重力加速度；J1为1阶第1类Bessel函数．根据图2的流域划分,文献[16]基于特征函数展开及边界匹配的势流半解析方法,可以得到各流域速度势函数,进而基于伯努利方程可以得到作用在浮子和阻尼板上的波浪载荷,分别将浮子和阻尼板定义为1和2,其受到的波浪激励力可以表示为：

(14)

由于自身运动受到的辐射作用力可以表示为:

F11=ω2ξ1(μ11+iλ11/ω)=

F22=ω2ξ2(μ22+iλ22/ω)=

(15)

由于其他浮体运动产生波浪而受到的作用力可以表示为：

F12=ω2ξ2(μ12+iλ12/ω)=

F21=ω2ξ1(μ21+iλ21ω)=

(16)

式中：下标表示后面浮体运动对前面浮体产生的影响,上述方程中速度势上标分别对应图2中的子流域．

2 水动力特性

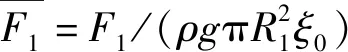
为了研究阻尼板半径的存在对浮子水动力的影响,由此设定阻尼板浸没深度为d2/h=0.16,半径分别为R2/h=0.10、0.12、0.15和0.18,分别从波浪激励力和辐射作用力两方面讨论．不同半径阻尼板时浮子及阻尼板受到的波浪激励力和辐射水动力系数如图3．从图中3(a)可以看出,浮子受到的波浪激励力随着阻尼板的半径变化几乎不变,但在入射波频率f较高时,有阻尼板的浮子比单个浮子受到的波浪激励力小,由此说明在入射波频率较大时,由于阻尼板存在,浮子底部流域速度偏大,由此作用在浮子底面的压强减小．值得注意的是,阻尼板自身受到的无因次波浪激励力随着阻尼板半径增大而增大．

由于阻尼板的存在,浮子的辐射水动力特性发生了很大的变化．浮子自身的附加质量和辐射阻尼随着阻尼板半径的增大而不断增大,如图3(c)和3(e),此外值得注意的是,浮子与阻尼板之间的相互作用辐射作用力体现为负的,如图3(d)和3(f)所示,由此说明浮子和阻尼板的自激励运动,均会促进对方的运动,且相互作用力的绝对值也随着阻尼板半径增大而逐渐增大．还可以看出,带阻尼板浮子比单个浮子受到的辐射作用力要大,且随着阻尼板增大,这种增大现象更加明显．阻尼板及其参数变化对浮子及阻尼板运动的影响见图3(g)和(h),浮子由于阻尼板的存在运动幅值增大,且其固有频率随阻尼板半径增大向低频移动,阻尼板自身运动随其半径增大减小,固有频率也逐步减小,由此可得,在给定波浪条件下,阻尼板会使得浮子运动加剧．

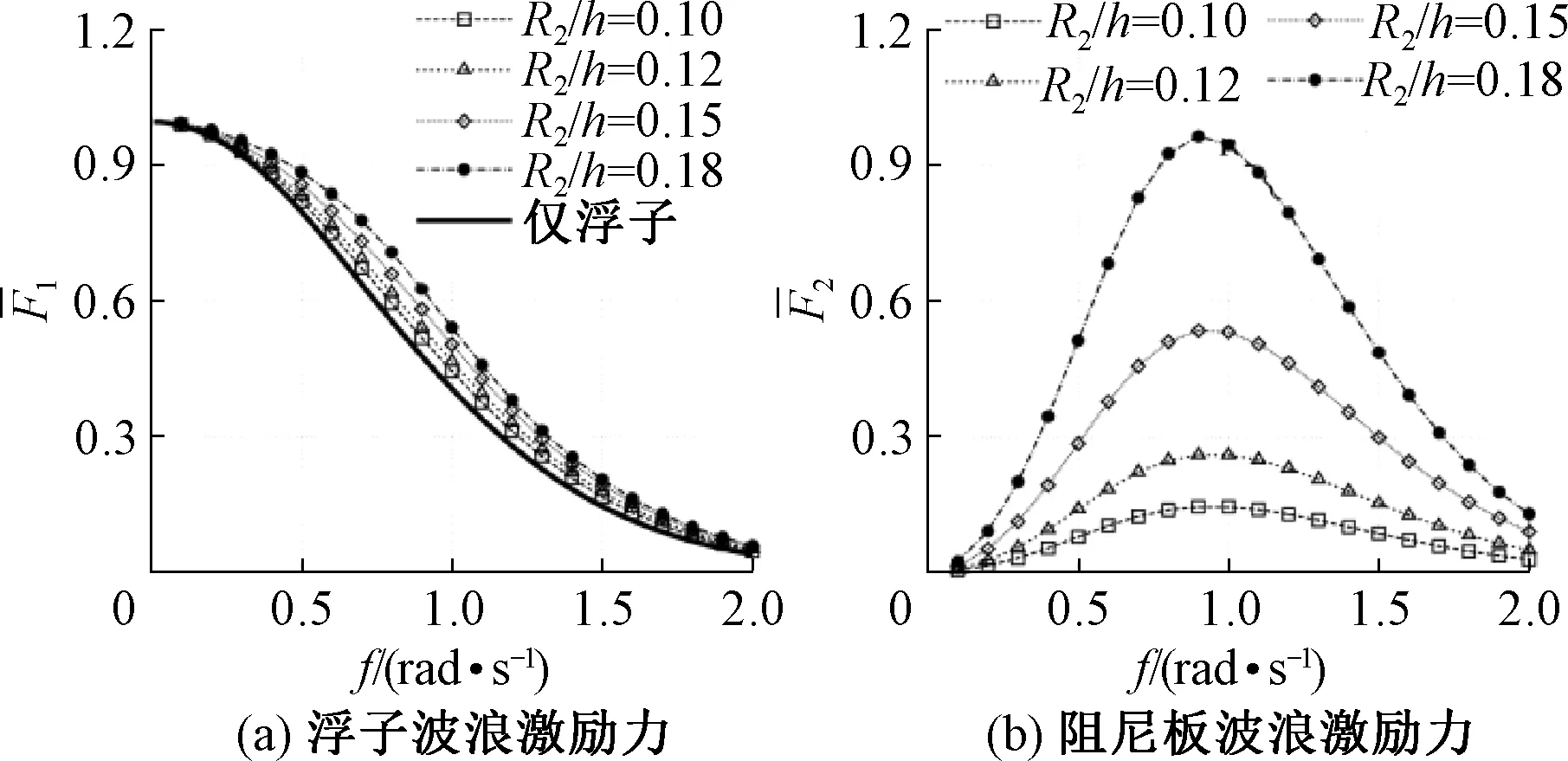
图3 d2/h=0.16,浮子及阻尼板受到的无因次 垂荡波浪激励力、附加质量、辐射阻尼和运动响应Fig.3 Non-dimensional waves excitation forces, added mass, radiation damping and motion of the buoy and plate in heave with d2/h=0.16

图4描述了阻尼板半径给定后,其浸没深度改变对浮体所受波浪激励力的影响．当增大阻尼板浸没深度时,浮子的波浪激励力保持不变,但阻尼板存在使得其小于单个浮子受到的波浪激励力,如图4(a),阻尼板受到的波浪激励力随着阻尼板浸没深度增加更加明显,尤其体现在高频部分,与阻尼板浸没深度呈反相关,如图4(b)所示．当增大其浸没深度,带阻尼板浮子由自激励运动所受的辐射作用力有略微减小,但总体上要远大于不带阻尼板时受到的作用力,如图4(c)和4(e)．同样的,浮子由于阻尼板作自激励垂荡运动产生的辐射波作用力呈现为负的,其中附加质量绝对值与阻尼板浸没深度呈反相关,而阻尼部分在低频时几乎没有变化,在高频时,也与浸没深度呈反相关,如图4(d)和(f)所示．改变阻尼板吃水对浮子及阻尼板自身运动响应的影响如图4(g)和(h)所示,可以看出,阻尼板吃水对浮子的运动几乎没有影响,但阻尼板吃水增加,其运动幅值迅速降低．

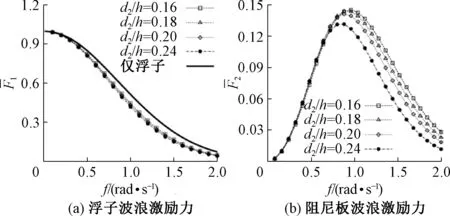
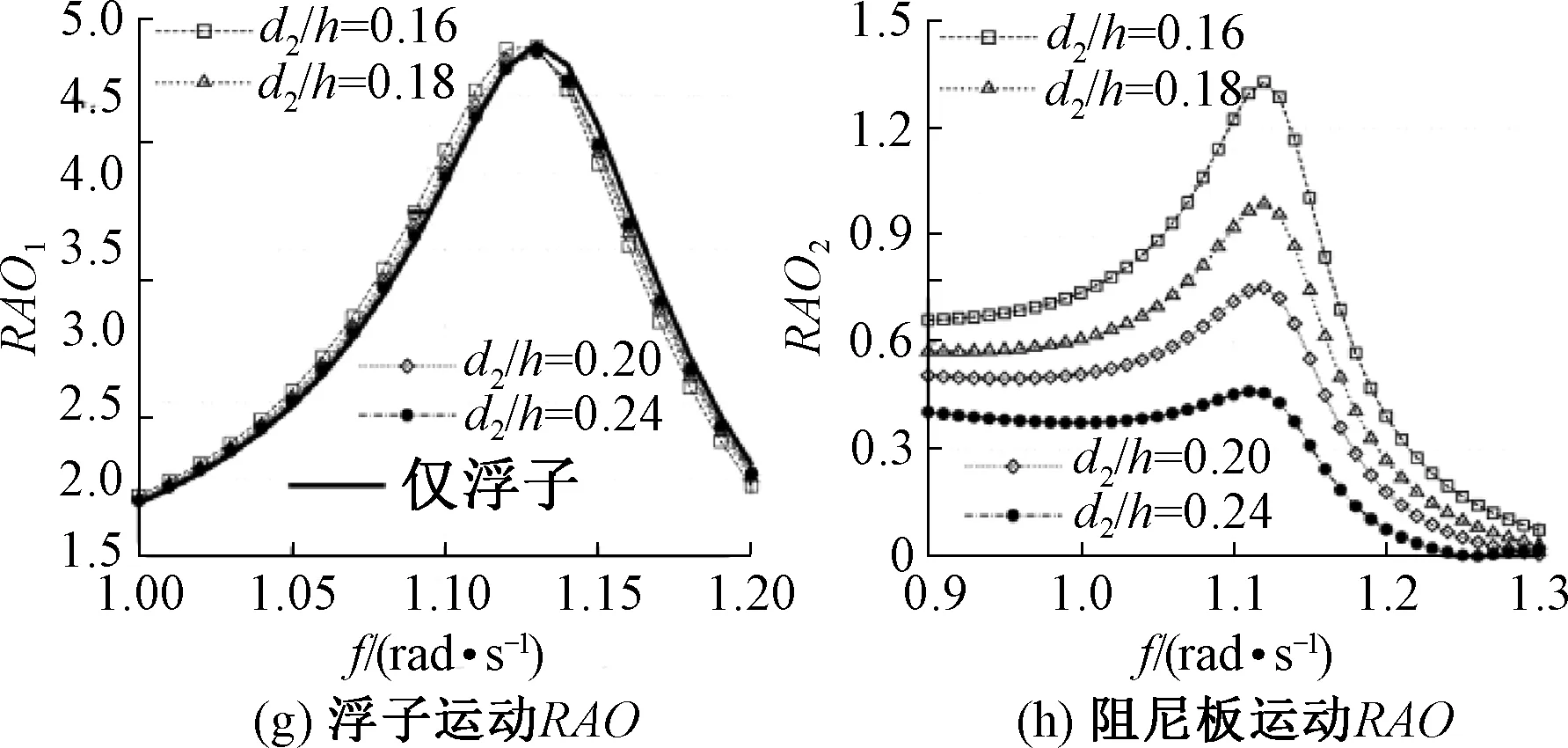
图4 R2/h=0.10,浮子及阻尼板受到的无因次垂荡波浪激励力、附加质量、辐射阻尼和运动响应Fig.4 Non-dimensional waves excitation forces, added mass, radiation damping and motion of the buoy and plate in heave with R2/h=0.16

3 波能转换特性

图5(a)和(b)分别描述了给定阻尼板浸没深度,改变其半径时系统的最优PTO阻尼及最优阻尼下的俘获宽度比．

图5 d2/h=0.16,装置的最优PTO阻尼及俘获宽度比Fig.5 Optimal PTO damping and capture width ratios with d2/h=0.16

从图5(a)可以看出,在入射波频率为1.15 rad/s时,单体式及双体式波能装置的最优PTO阻尼系数有同样的最小值100 kNs/m,而在这个频率之后,两类装置的最优PTO阻尼系数相当,且几乎不随阻尼板半径变化．但在入射波频率小于1.15 rad/s时,不带阻尼板装置的最优阻尼系数呈现随频率增大迅速衰减的现象,而带阻尼板的双浮体装置的最优阻尼系数随频率增大出现极大值然后迅速减小到极小值,值得注意的是,极大值对应的入射波频率与阻尼板半径有很大关系,在给定阻尼板浸没深度后,峰值频率随阻尼板半径增大而减小,但对应的峰值是逐步增大的．

对于文中选定的浮子,给定阻尼板厚度及浸没深度,装置的最优俘获宽度比在频率大于1.15 rad/s时几乎不受阻尼板的半径影响,与单浮体的一样,如图5(b)．但是当入射波频率小于1.15 rad/s时,它们的最优波能俘获能力表现出很大区别,特别的,带阻尼板的双浮体波能装置的最优俘获宽度比表现出与最优PTO阻尼相似的特点,随着频率的变化会出现峰值．给定阻尼板浸没深度,该峰值处的频率随着其半径增大逐步减小,而对应峰值呈现出先增大后减小的趋势,由此说明,当阻尼板浸没深度给定后,存在最优的阻尼板半径使得装置的最优俘获宽度比峰值达到最大．

与给定阻尼板浸没深度类似,当给定阻尼板半径而变化其浸没深度时,可以看出最优PTO阻尼系数仍然在入射波频率为1.15rad/s时,达到其最小值100 kNs/m,且最大值对应的频率随着浸没深度增大而减小,如图6(a),不同的是,峰值对应的频率及峰值大小的变化很微弱,由此说明阻尼板浸没深度对装置的影响较小．在最优PTO阻尼下俘获的波浪能如图6(b),装置的最优俘获宽度比在入射波频率大于1.15 rad/s时,几乎不受阻尼板浸没深度的影响．但当波浪频率小于1.15 rad/s时,给定阻尼板的半径情况下,增大其浸没深度,可以发现,俘获宽度比峰值及对应频率的变化相较于给定阻尼板吃水变化其半径时要小很多．进一步地,通过对比双浮体与单浮体装置的最优波能俘获,发现双浮体装置在较小的频率附近几乎没有能量获取,而单浮体在低频仍然有一定的能量转换,但是通过适当调整阻尼板半径和吃水,可以使得装置的最优波能俘获有较大的频率带宽．

图6 R2/h=0.10,装置的最优PTO阻尼及俘获宽度比Fig.6 Optimal PTO damping and capture width ratios with R2/h=0.10

4 结论

(1) 阻尼板的存在会降低浮子底部绕射波产生的激励力,但其运动产生的作用在浮子上的辐射作用力大于单独浮子运动受到的辐射作用力,且这种作用主要体现在惯性载荷部分;

(2) 阻尼板浸没深度对浮子水动力的影响主要表现在高频部分,而其参数变化对系统波能转换的影响只在低于最大耦合共振频率部分体现,且相较于浸没深度,浮子水动力特性对阻尼板半径的变化更加敏感;

(3) 浸没阻尼板是系统出现两个耦合共振频率,阻尼板参数的影响主要体现在较小的共振频率,阻尼板构型参数变化对系统较大耦合共振频率处的最优波能转换没有影响,但是随着其半径和浸没深度增加,较小共振频率的最优波能转换均先增大后减小,即在给定浮子参数情况下,存在阻尼板半径和浸没深度使得系统波能转换最优．