钢渣土工应用渗透特性试验研究

2020-05-19闫家涛王丽艳

江苏科技大学学报(自然科学版) 2020年2期

闫家涛,王琪,黄祥,王丽艳

(江苏科技大学土木与建筑工程学院, 镇江 212003)

钢渣是钢铁冶金工业产生的废弃物,全国每年仅钢渣排放量就超过1亿吨,总量已积存2亿吨以上[1],且每年仍以数千万吨的排渣量递增．文献[2]总结了英国4种工业废弃物在沥青路面上的应用,其中包括废弃钢渣和废旧轮胎;文献[3]针对台湾地区诸多工业废弃物循环再利用的可持续性进行了分析,其中也包括废弃钢渣．

钢渣在国外被广泛用于道路路基的垫层,如法国、德意志联邦共和国、加拿大等国都把钢渣用作铁路道碴和道路材料,做法是先将加工后的钢渣存放3～6个月,待体积稳定以后再使用．文献[4]将钢渣和碎石混合作为柔性路面垫层,探讨钢渣掺入量对混合料的力学性能的影响．文献[5]将钢渣加入混凝土中研究混凝土的力学性能．文献[6]将橡胶颗粒掺入钢渣研究混合料的压缩力学性能．

渗透性是岩土工程方向研究的关键课题之一,而渗透系数作为渗透性最重要的参数,其变化规律对土体强度和剪切变形有着重要影响,也必然与工程的安全紧密相关．土的渗透系数主要受土的种类、级配、密实度和温度等因素影响,目前主要针对常规土的渗透性能研究较多．

文献[7]利用常水头渗透仪进行不同粗粒含量砂土的渗透性能试验;文献[8]对粉砂土路基进行渗透试验;文献[9]研究加入黄土后粉煤灰的渗透特性．文献[10]针对钙质砂渗透特性及其影响因素进行研究．文献[11]研究土的粒径、级配对于渗透系数的影响．目前基本公认的有效粒径d10和孔隙比e对渗透系数有影响,但两者以何种形式出现在渗透系数的理论预测公式中,目前尚未有统一的认识[12]．

近些年,粉煤灰已被大量用于筑坝和基础填筑的施工中,在许多方面表现出优越的工程性能[13]．碱渣与粉煤灰等拌和可制成工程土,代替一般工程土作为道路基础或大面积填垫材料的途经[14]．但是,粉煤灰缺少必要的粘聚力,对水的反应较为敏感,给工程的安全运行带来不利影响．已有研究表明钢渣具有胶凝性[15],如果钢渣渗透性能良好,将比粉煤灰更适合作为填料用于路基、建筑地基等实际工程．

因此,有必要研究钢渣土工应用的渗透性能,国内外对此方面的研究尚不多见．文中通过考虑相对密实度和级配2种重要因素开展纯钢渣的常水头渗透试验,研究纯钢渣土工应用的渗透特性．

1 基本物理特性试验

1.1 钢渣颗粒分析试验

试验材料为江苏张家港市永钢集团生产过程中产生的废弃钢渣,所取的废弃钢渣已陈化堆放8个月以上,化学性质稳定,可直接用于土工中,其天然堆积状态如图1．

图1 堆积的废弃钢渣Fig.1 Stacked steel slag

首先采用筛分法对上图钢渣进行颗粒分析试验,所得3种钢渣筛分试验结果见图2．为了明确区分3种钢渣,根据钢渣的粒径范围,文中定义粒径小于1 mm的粒组质量超过总质量50%的钢渣为细钢渣,粒径大于1 mm小于5 mm的粒组质量超过总质量50%的钢渣为粗钢渣,粒径大于2 mm的粒组质量超过总质量50%的钢渣为砾钢渣,下文钢渣均按此定义划分．

图2 3种钢渣的级配曲线Fig.2 Grading curves of three kinds of steel slag

根据颗分试验结果,计算出3种钢渣的粒径参数,见表1．3种钢渣的不均匀系数Cu都大于5,但细钢渣和砾钢渣曲率系数Cc介于1与3之间,级配良好,而粗钢渣曲率系数Cc>3,级配不良．

表1 3种钢渣的粒径参数Table 1 Particle size parameters of three kinds of steel slag

1.2 钢渣最大与最小干密度试验

纯钢渣常水头渗透试验的控制因素之一为钢渣的相对密实度,因此需要通过试验测得3种钢渣的最大和最小干密度,随后计算分别得到各钢渣的相对密实度．试验材料如图3．

图3 试验材料线Fig.3 Test materials

计算得到的3种钢渣的最大、最小干密度见表2．

表2 3种钢渣最大与最小干密度Table 2 Maximum and minimum dry density of three kinds of steel slag g·cm-3

1.3 钢渣的比重试验

钢渣的比重为实测指标,其测量精度直接影响其他指标的准确性．由于粗、细两种钢渣粒径都在5 mm以内,故选用比重瓶法测试,砾钢渣中存在近20%的颗粒大于5 mm,因此选用浮称法测定．

所测比重数值见表3,并将其与传统土比重进行比较,得出3种钢渣的比重均大于常规土的比重,细钢渣和粗钢渣比重相近．砾钢渣比重相比于粗、细钢渣较小,但也高于砂土等常规土的比重．

表3 3种钢渣与常规土的比重对比Table 3 Comparison of specific gravity between three kinds of steel slag and conventional soils g·cm-3

2 纯钢渣的渗透特性试验

2.1 试验方案

考虑相对密实度、颗粒级配两种因素开展3种级配18组试验,相对密度采用木锤击实法控制．每组平行试验测定3次,试验在室温下进行,为消除温度的影响,试验时测试水温,试验结果最终统一修正为20 ℃下的渗透系数．表4为3种钢渣渗透试验相对密实度的设定水平．

表4 渗透试验相对密实度的设定水平Table 4 Setting level of the factors considered in the penetration test

注:*表示该值为相对密实度设计值,结果分析时按照实测值为依据

2.2 试验仪器与试验方法

本试验器材为TST-70型常水头渗透仪,装置如图4．试验时取烘干钢渣6 kg,将试样分12层装入圆筒．

图4 TST-70型渗透仪Fig.4 TST-70 type permeameter

2.3 试验结果与分析

2.3.1 渗透系数k与相对密度(Dr)关系

在坐标系中绘制渗透系数与相对密度k-Dr关系曲线，如图5,可以看出:(1) 钢渣相对密实度越大,渗透系数越小,这是由于相对密实度越大,钢渣越密实,内部孔隙越小,小颗粒填充大颗粒间隙,同时压缩了孔隙空气,水自由流动的阻力增大;(2) 细钢渣与粗钢渣的渗透系数在密实度较低时(小于30%)下降缓慢,在相对密实度40%～60%之间,渗透曲线出现拐点,渗透系数急剧减小,60%之后曲线下降趋势放缓;砾钢渣的渗透系数则随着相对密实度的增加显著降低,达到70%后下降趋势放缓,规律与细钢渣和粗钢渣有所不同．

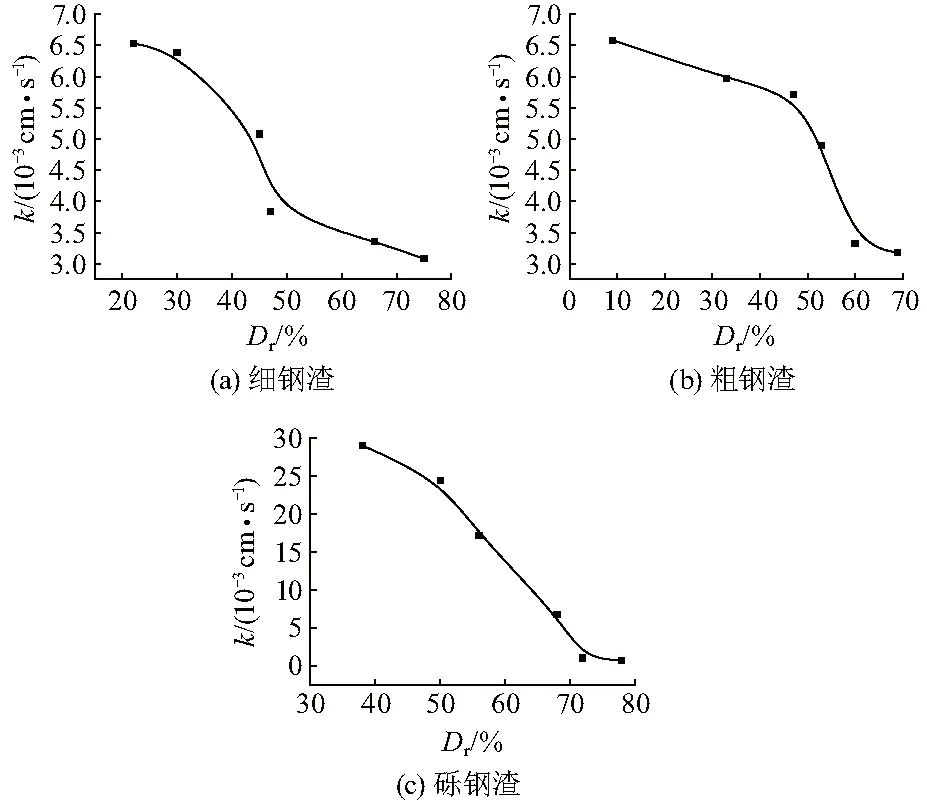
图5 3种钢渣渗透系数随相对密度变化的曲线Fig.5 Permeability curves of three types of steel slag with relative density changes

2.3.2 渗透系数k与孔隙比(e)关系

利用式(1)计算出各状态下的孔隙比,绘出钢渣渗透系数(k)随孔隙比(e)的变化曲线如图6．由图6可以看出,钢渣的渗透系数随其孔隙比的增大而增大,渗透系数在孔隙比0.5～0.65之间增长快速,之后增长趋势趋于平缓．

(1)

式中：Gs为钢渣的比重;ρd为钢渣干密度;ρw为4℃下水的密度．

图6 3种钢渣随孔隙比变化的渗透曲线Fig.6 Permeability curves of three kinds of steel slag with void ratio changes

细钢渣在制样过程中压实难度大,渗透系数均稳定在10-3数量级,且数值相差不大;粗钢渣级配不良但粗颗粒较多,粒径范围大,因此渗流速度明显快于细钢渣,管口出水呈水流状,渗透系数均在10-2数量级;根据级配曲线可以看出,砾钢渣粒径分布范围更大,大颗粒多且级配良好,更容易压密实,随着孔隙比的减小,管口出水由水流状变化到水滴状．当孔隙比在0.52以上并逐渐增大时,砾钢渣的渗透系数数量级为10-2,且增长快速;渗透性能类似于粗钢渣,当孔隙比在0.52以下并逐渐减小时,砾钢渣的渗透系数很小,且经过10-3达到10-4甚至更小数量级．

2.4 纯钢渣渗透系数预测公式

由于渗透仪器功能的限制,试验过程中无法控制钢渣达到完全密实,为了全面了解钢渣不同状态下的渗透特性,有必要推导出纯钢渣的渗透系数预测公式．

文献[19] 基于纯砂渗透实验观测数据提出渗透系数经验公式,如式(2),式中c为一个常数,在1～1.5之间变化;Casagrande提出了细中砂的渗透系数的简单关系,见式(3),该公式表明渗透系数与孔隙比以及孔隙比为0.85下的渗透系数有关;Kozeny和Garman(1956)推导出了新的粗粒土渗透系数计算公式,见式(4);Amer和Awad(1974)基于前人的研究和自己试验结果对照,得出渗透系数公式(5),式中C1为常数．

k=cd102

(2)

k=1.4e2k0.85

(3)

(4)

(5)

式中：C为常数，取值为1.0～1.5之间；Cs为形状系数；Ss为土壤固体颗粒单元表面积；T为迂曲度;μ为粘滞系数;Cu为不均匀系数；d10为有效粒径,mm.

以往的公式表明,粗粒土的渗透系数与孔隙比已经形成一种关系,即,

(6)

Chapuis[19](2004)提出了k的经验关系方程,如式(7),该公式对于自然的、均匀的砂和砾石是有效的,渗透系数预测范围在10-1～10-3之间,并可以扩展用于没有塑性的天然粉砂,但是对于粉碎的材料或有一定塑性的粉土是无效的．

(7)

文中所研究的废弃钢渣是具有胶凝性和粘聚力的碎散材料,但是宏观颗粒又类似于砂和砾石,因此,钢渣的渗透系数计算公式可基于Chapuis经验公式进行修正．经计算和研究发现,Chapuis公式经修正后适用于细钢渣和粗钢渣的渗透系数计算,如式(8)，(9)．经计算,细钢渣渗透系数的公式预测值与试验测试值偏差很小,除个别偏差在20%左右,其他偏差均在10%以内;粗钢渣渗透系数的公式预测值与试验测试值偏差较小,但存在2个值偏差超过20%．但是,无论是细钢渣还是粗钢渣,渗透系数预测值与试验测试值的数量级吻合,在同一数量级上,表明文中提出的2个修正公式预测粗细钢渣的渗透系数具有合理性和可靠性．

(8)

(9)

由于砾钢渣在不同密实度下渗透系数变化范围很大,横跨4个数量级(10-5～10-2),经过验算以往的经验公式发现都不适用,也无法对经验公式进行修正．所以,这里采用文中试验测试数据进行曲线拟合，如图7.

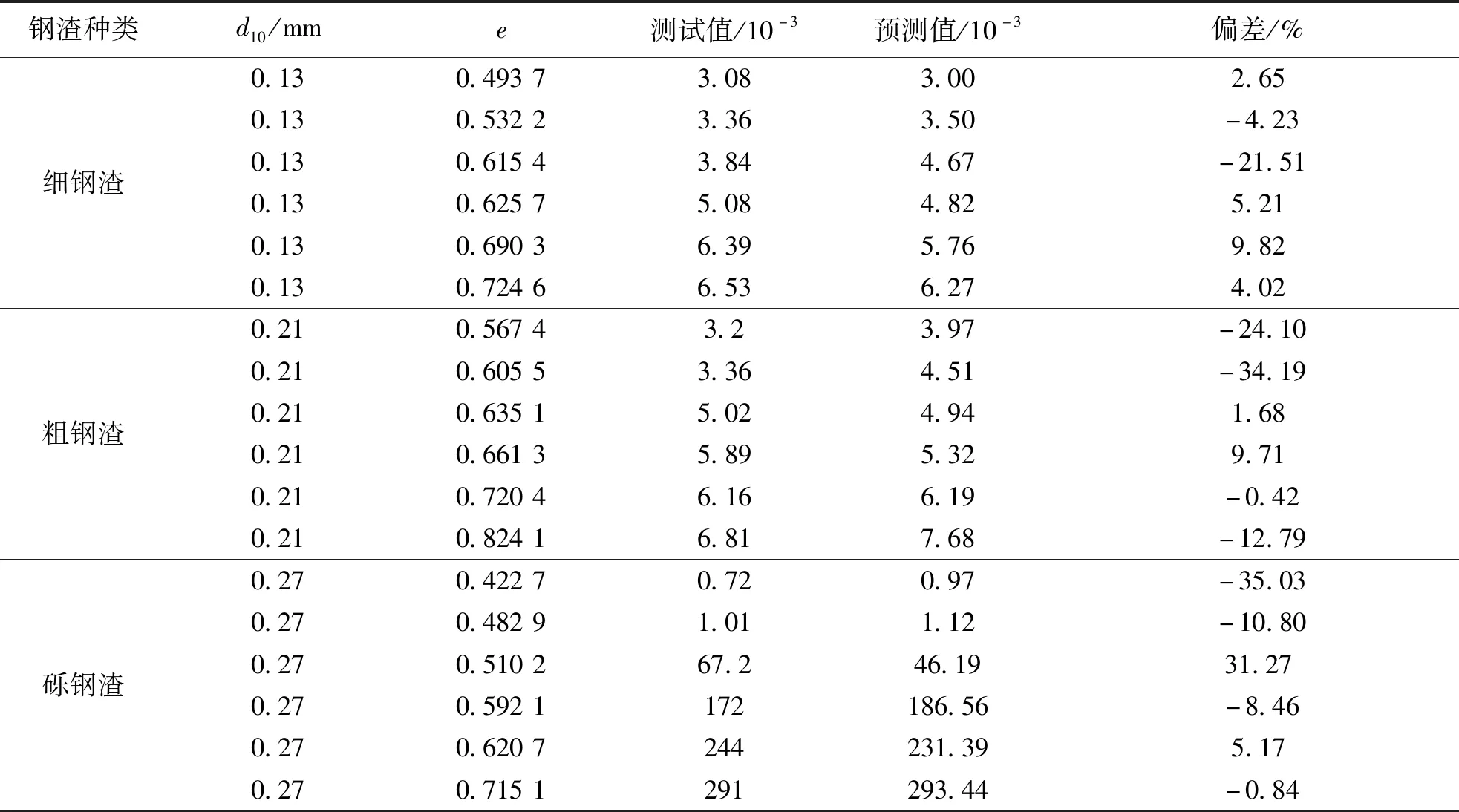
表5 细钢渣、粗钢渣的渗透系数测试值与公式预测值对比Table 5 Comparison between actual value and formula calculation value of permeability coefficient of fine steel slag and coarse steel slag

图7 砾钢渣渗透系数变化的拟合曲线
Fig.7Fitting curve of gravel steel slag

permeability coefficient

推出适合砾钢渣渗透系数计算的拟合公式,见式(10),拟合得到的砾钢渣渗透系数计算公式拟合度达到97.2%．

(10)

3 钢渣土工应用分析

为了能够清晰地对比钢渣与传统土渗透系数的范围,绘制了综合图,如图8．经过比较,得到密实情况下(相对密实度>55%)砾钢渣渗透性能(渗透系数10-5～10-3cm/s)与粉煤灰[20]相当;粗钢渣和细钢渣渗透性能优于粉煤灰(10-5～10-3cm/s),劣于纯砾(>10-1cm/s),与纯砂和低砾含量的混合物相当．

图8 钢渣与常规土料的渗透系数比较Fig.8 Comparison of permeability coefficient between steel slag and conventional soils

传统砂土和粉煤灰常用于路基填料,砂砾土常用于水闸大坝下游工程作垫层,但是由于砂土和粉煤灰基本不具有胶凝性和粘聚力,砂土会受水流冲刷和风蚀易损坏,粉煤灰质轻,水稳定性弱于钢渣．由前面3种纯钢渣的渗透特性研究得出纯钢渣的渗透性能良好,且钢渣具有胶凝性和粘聚力,因此,钢渣或许比砂土与粉煤灰更适合作为填料用于路基和建筑地基等工程回填中．

道路基层填充必须有较好的透水性,由前面研究得出:相对密实度>55%的砾钢渣与粉煤灰渗透性能相当,而细钢渣和粗钢渣渗透性能优于粉煤灰,与纯砂和低砾含量的混合物相当．因此,土工应用中细钢渣、粗钢渣和密实状态下的砾钢渣都可以替代粉煤灰,细钢渣和粗钢渣还可以替代纯砂和低砾含量的混合物．