基于容差关系知识依赖的属性约简算法研究
2020-05-21夏冰莹
夏冰莹, 吴 陈
(江苏科技大学 计算机学院, 镇江 212003)
粗糙集理论由波兰学者PAWLAK Z在1982年研究不完整数据和不精确知识的表达中提出[1-3],它能有效阐述和处理模糊、不完整等各种不完备信息,并从中发现潜在知识,揭示隐含规律.目前,粗糙集理论在许多领域取得了广泛应用,并且在机器学习领域中成为一个较新的研究热点[4].该理论的核心是不可分辨关系,也就是等价关系.该关系在分类过程中产生,对知识库中知识间的关系研究起到了至关重要的作用.但是在现实生活中,由于测量误差、数据冗余等原因,造成信息系统的属性缺失现象普遍存在.在不完备信息系统[5-7]中,根据等价关系对论域进行划分是不合理的.为了提高数据分析处理的准确性,可以对传统的基于等价关系的近似集模型进行改进,将等价关系弱化为其他二元关系,如容差关系[8]、相似关系[9]、非对称相似关系[10]等.文中基于容差关系对知识的完全依赖和不完全依赖给出了定义,并给出了相关性质.
属性约简[11-12]是粗糙集理论的核心内容之一,可以从信息系统中去除冗余知识,从而得到较为精简的知识.在完备信息系统中,关系属性约简已经有很多有效的方法.由于信息缺失现象广泛存在,在不完备环境下对属性约简,也引起了人们的广泛关注.如文献[13]中分析了一种基于下近似二进制可分辨矩阵,并给出了一种直接的约简算法;文献[14]以相似关系作为不可分辨关系,以属性重要度为启发提出了一种基于相似关系的属性约简方法.文中通过引入知识粒度[15]、知识依赖度[16]等概念,对不完备信息系统的属性重要度进行了定义,提出了两个对属性进行约简的算法,并通过实验证明算法可以得到最小约简.
1 概念术语
在现实生活中,绝大多数信息系统都是不完备的,属性缺失是其主要问题.对于一个对象,一些属性值遗漏或不能确定.通常未知属性有两种不同解释,即遗漏型空值和缺席型空值[17].文中研究遗漏型空值,即未知属性实际上是存在的,只是由于某种原因,目前未能获得该值.
定义1一个不完备信息系统(incomplete information system, IIS)[5]为四元组S=(U,AT,V,f),其中,U为论域,是一个非空有限对象集;AT为属性的非空有限集合,对于∀a∈AT, 有a:U→Va;V为属性值域,其中Va为属性a的值域,可包含空值“*”;f为信息函数,对于∀a∈A,∀x∈U,有f(x,a)⊆Va.
定义2设S=(U,AT,V,f)为一个不完备信息系统,对于∀a∈AT,则基于a容差关系,SIM(a)定义[18]为:
SIM({a})={(x,y)∈U×U|a(x)=a(y)∨a(x)=*∨a(y)=*}
(1)
定义3对于 ∀A⊆AT,记[19]
SIM(A)=∩a∈ASIM({a})
(2)
显然SIM(A)为一个容差关系,具有自反性和对称性,而不满足传递性.
定义4对于∀A⊆AT,SA(x)表示对象集[19]{y∈U|(x,y)∈SIM(A)}.
对于A而言,SA(x)为与x可能可分的对象的最大集合.DA(x)表示对象集{y∈U|(x,y)∉SIM(A)};对于A而言,DA(x)为与x可能不可分的对象的最大集合.令U/SIM(A)={SA(x)|x∈U}表示分类,U/SIM(A)中的任何元素称为相容类.
定义5设S=(U,AT,V,f)是一个不完备信息系统,∀X⊆U,∀A⊆AT,X基于容差关系的下、上近似集[20]分别为
A(X)={x∈U|SA(x)⊆X}
(3)
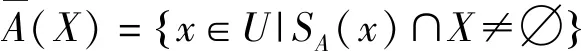
(4)
2 不完备信息系统下的知识依赖度
定义6容差关系SIM(a)可以等价为关系R,关系R的相容度cmpbl(R)定义为:
cmpbl(R)=|{(x,y):(x,y)∈R}|
(5)
实际上,R的相容度cmpbl(R)就是R的基数,即cmpbl(R)=|R|.
定义7关系R的粒度定义为:
(6)
式中,n为论域中元素的个数,n=|U|.
定义8在不完备信息系统中,对于任意属性a, 定义属性a的相容度为:
cmpbl(a)=cmpbl(Ra)
(7)
式中,Ra为由属性a所生成的容差关系,即Ra=SIM(a).
定义9在不完备信息系统中,对于任意属性子集P,定义属性子集P的相容度为:
cmpbl(P)=cmpbl(Rp)
(8)
式中,Rp为由属性子集P所生成的容差关系,即Rp=SIM(P).
于是,属性及属性子集的相容度具有下列特性:
(1)cmpbl(a,b)=cmpbl(Ra∩Rb),其中Ra和Rb分别为属性a和b构成的容差关系.
(2)cmpbl(a,b)≤min{cmpbl(Ra),cmpbl(Rb)}.
(3)cmpbl(a1,a2,…,an)=
cmpbl(Ra1∩Ra2∩…∩Ran)≤
cmpbl(Rak1∩Rak2∩…∩Rakl)
式中,{k1,k2, …,kl}⊆{1,2…,n}.
(4) 0≤cmpbl(a,b)≤n2.
(5) 当所有对象在属性a和属性b上值相等时,cmpbl(a)=cmpbl(b),gd(a)=gd(b).
(6) 当所有对象在属性a和属性b上值都不为*,且都不相等或相异时,cmpbl(a,b)=0.
对于不完备信息系统,定义属性间的完全依赖关系如下.
定义10对于不完备信息系统中属性a和b,若对∀x,y,当f(x,a)=f(y,a)∨f(x,a)=*∨f(y,a)=* 时,必有f(x,b)=f(y,b)∨f(x,b)=*∨f(y,b)=*,则称属性b完全依赖于属性a,记为a⟹b,或a→b.
定理1当a→b时,有:
(1)Ra⊆Rb.
(2) 对∀x∈U,Sa(x)⊆Sb(x).
(3)cmpbl(Ra)≤cmpbl(Rb).
证明:(1) 当a→b时,对任意x,y,当f(x,a)=f(y,a)∨f(x,a)=*∨f(y,a)=*有
f(x,b)=f(y,b)∨f(x,b)=*∨f(y,b)=*,即(x,y)∈Ra⟹(x,y)∈Rb,所以,Ra⊆Rb.
(2) 对∀y,若y∈Sa(x),即(x,y)∈Ra,必有(x,y)∈Rb,则y∈Sb(x).于是,Sa(x)⊆Sb(x).
(3) 由Ra⊆Rb,必有:
cmpbl(Ra)≤cmpbl(Rb).
定义11对于不完备信息系统属性子集P和Q,若对∀a∈P,∀b∈Q,∀x,y∈U,x≠y,都有当f(x,a)=f(y,a)∨f(x,a)=*∨f(y,a)=*时,必有f(x,b)=f(y,b)∨f(x,b)=*∨f(y,b)=*.则称属性子集Q完全依赖于属性子集P,记为P→Q.
定理2对于不完备信息系统中属性子集P和Q,P→Q当且仅当∀a∈P,∀b∈Q,a→b.
定理3当P→Q时,有:
(1)RP⊆RQ.
(2) 对∀x∈U,SP(x)⊆SQ(x).
(3)cmpbl(RP)≤cmpbl(RQ).
对于一个不完备信息系统,两个属性之间不一定都具有完全依赖性,通常可能只存在部分依赖程度的关系.文中将从更广义的角度考虑两种不完全依赖情况下知识依赖度的计算方案.
首先从单属性之间的部分依赖度定义开始,接着再讨论属性子集之间的部分依赖度.
情况1:当属性a,b分别为条件属性与决策属性,且b中不含有空值时.
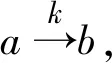
(9)
情况2:当属性a,b均为条件属性,且a和b均可能包含空值时.
定义13设a和b为两个属性,定义b以依赖度k依赖于a,则:
(10)
不难验证,
(11)
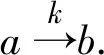
k=1 iffk=gd(Ra∩Rb)=gd(Ra)
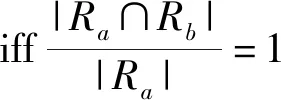
对于在前面所定义的完全依赖,由a→b,必有Ra⊆Rb,即当b完全依赖于a时,按此式计算得到的b依赖于a的依赖度k=1.由此可见,完全依赖是部分依赖的特例.
当k(a,b)=1时,记a⟹b.k(a,b)=0
iffgd(Ra∩Rb)=0 iffRa∩Rb=∅.
当k=0时,b不依赖于a.
定义14对两个属性子集P和Q,Q依赖于P的依赖度定义为:
(12)
k(P,Q)=1,gd(RP∩RQ)=gd(RP) iffRP⊆RQ,又因,gd(RP∩RQ)≤{gd(RP),gd(RQ)},当RP⊆RQ时,gd(RP)≤gd(RQ).
以汽车的属性值[21]为例,说明不完备信息系统中的知识依赖度及其性质.
例1设U={1,2,3,4,5,6},AT={P,M,S,X},式中P,M,S,X分别表示价格、里程、规格、最大速度;V={high,low,full,compact,*}.则表1给出了一个不完备信息系统.
每个属性子集或由该属性子集生成的关系的粒度计算结果为:

表1 一个不完备信息系统Table 1 An incomplete information system
3 不完备信息系统下知识依赖度的性质
考虑条件属性可能含有空值的情况,条件属性和决策属性不含空值时,可以看作该情况的一种特例.
3.1 完全依赖下依赖度的特性
定理4(传递性)若a→b,b→c则a→c.
按前面定义的完全依赖,a→biffRa⊆Rb,则Ra⊆Rb,Rb⊆Rc⟹Ra⊆Rc.
现在用新定义的依赖度加以证明.
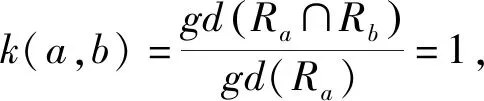
得gd(Ra∩Rb)=gd(Ra).
同理可得gd(Rb∩Rc)=gd(Rb)
则gd(Ra∩Rc)=gd(Ra∩Rb∩Rc)=gd(Ra∩Rb)=gd(Ra)
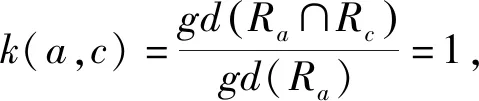
例1在表1中,S⟹P,P⟹M,S⟹M,因此,定理4成立.
定理5(增广性)若a→b则a,c→b,c.
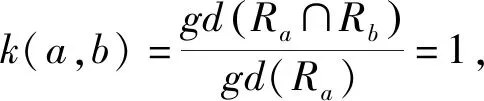
由Ra∩Rc⊆Rb∩Rc,可以得到Ra,c⊆Rb,c因此a,c→b,c成立.
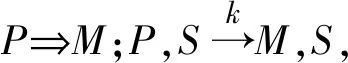
定理6(左增广性)若a→b,则a,c→b.
证明:由Ra⊆Rb,可以得到Ra,c=Ra∩Rc⊆Rb因此a,c→b成立.

3.2 不完全依赖下依赖度的特性
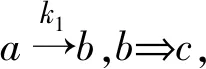
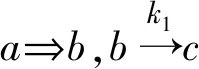
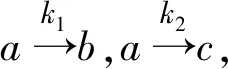


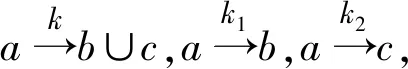


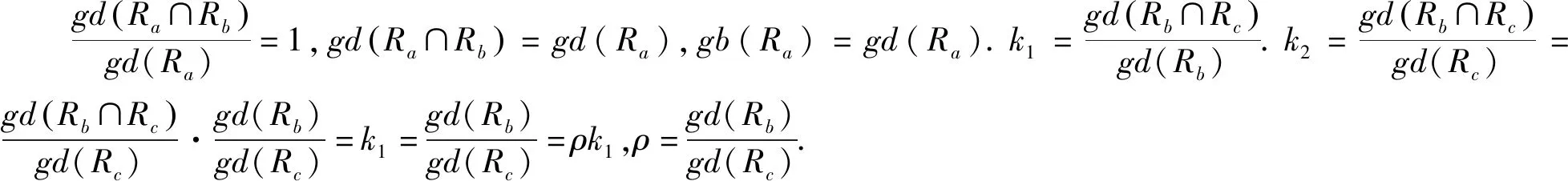
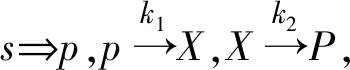
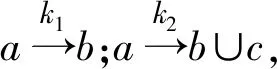
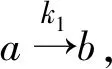

4 属性的重要度分析
定义15已知不完备信息系统IIS=(U,AT∪{d},f,V),对于∀A⊆AT,d为决策属性.若A-{a}⟹A,则SIM(A)=SIM(A-a).
证明:
由A-{a}⊆A可以得到SIM(A)⊆SIM(A-{a}),
因为A-{a}⟹A所以SIM(A-{a})⊆SIM(A),
因此SIM(A)=SIM(A-{a}).
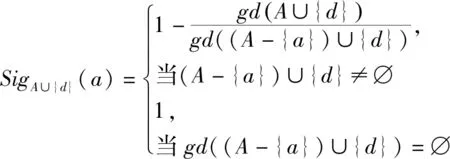
(13)
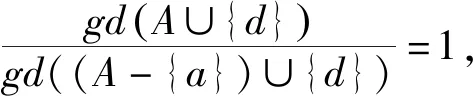
定义17给定不完备信息系统IIS=(U,AT,f,V).对于∀A⊆AT,a∈A≠∅.已知属性a在A中的重要度是由A中去掉a后引起的知识粒度变化的大小来衡量的.也就是说,对于一个属性集合,去掉一个属性引起的知识粒度变化量越大,该属性对此属性集就越重要.若SigA(a)>0,即gd(A∪{d}) 定义18给定不完备信息系统IIS=(U,AT,f,V).对于∀A⊆AT,A中所有核属性所构成的属性子集记为CORE(A),即CORE(A)={a:SigA(a)>0,a∈A}. 定义19给定不完备信息系统IIS=(U,AT,f,V).对于∀A⊆AT,B⊆A,若SIM(B)=SIM(A),且不存在B′⊂B,使得SIM(B′)=SIM(A),则称B为A的一个约简.A的所有约简作为元素构成的集合记为RED(A). 可以证明,CORE(A)=B,B∈RED(A). 定理11给定不完备信息系统IIS=(U,AT,f,V).对于∀A⊆AT,a∈A,则下列结论等价. (1)a是A中不重要的,即SigA(a)=0. (2)a是A中冗余的,即SIM(A-{a})=SIM(A). (3)A⟹a. (4)A-{a}⟹A. (5)k=k(A-{a},A)=1. 依据属性重要度作为启发式信息可设计求信息系统属性约简的两个算法,一个从核属性集出发,采用自底向上的方法,通过每次加入一个重要度大的属性来求解,另一个采用自顶向下的方法从整个属性集出发,每次去掉一个重要度最小的属性来求解. 算法1由核属性集出发每次加入一个属性重要度最大的属性求最小约简. 输入:不完备信息系统IIS=(U,AT∪{d},f,V),其中∀A⊆AT. 输出:一个最小约简B∈RED(A). 步骤: (1) 求核,CORE(A)对任意属性a∈A,计算SigA∪{d}(a),所有在A中SigA∪{d}(a)值大于0的属性都是核属性,即CORE(A)={a:SigA(a)>0,a∈A}. (2) 初始化B值,B=CORE(A). (3) 判断SIM(B)=SIM(A)是否成立,若成立,则转步骤(6),否则转步骤(4). (4) 计算所有属性x∈A-B的值SigB∪{x}(x),取属性a,满足下列条件: 即具有最大重要度的属性a. (5)B=B∪{a},将步骤(4)中计算的具有最大重要度的属性a加入B. (6) 输出A的一个最小约简B. 令B=CORE(A)={S,X},因为SIM(B)=SIM(A),所以得到一个最小约简REDUCT=B={S,X}. 算法2由属性集出发每次减少1个重要度最小的属性直到求出一个最小约简. 输入:不完备信息系统IIS=(U,AT∪{d},f,V),其中∀A⊆AT. 输出:A的约简RED. 步骤: (1) 令RED=A. (3) 判断,若SIM(RED-{a})≠SIM(A),则转步骤(4),否则RED=RED-{a},将属性a从RED中删除,转步骤(2). (4) 输出约简RED,算法结束. 为了进一步考察文中算法的有效性,选取了5组UCI数据集进行实验分析,数据信息的基本描述如表2.实验环境为PC机,Windows 8操作系统,MATLAB R2014a实验平台. 针对不完备信息系统,选用表2中的5组UCI数据,对文中的两个算法及文献[22]中的约简算法进行约简个数比较. 表2 文中算法与文献[22]中算法进行属性约简结果比较Table 2 Comparison of the reduction result between our algorithm and the algorithm in literature[22] 文中用UCI中的数据库计算决策精度(正确率):一部分数据作训练数据提取出决策,另一部份数据作测试,正确率可计算出来.如用类似于1/10法,有100个数据,每次用90个数据提取决策规则,用剩下的10个数据作测试数据,得到每次正确个数的总和再除以10得到平均正确率.图1为算法1与算法2对表2中5组UCI数据的分类精度. 图1 算法1与算法2分类精度对比Fig.1 Comparison of classification accuracy between algorithm 1 and algorithm 2 从表3的结果可以分析得出:从约简个数来看,文中算法与其他文献相比,属性个数少于或等于其结果. 表3 数据集描述Table 3 Data sets description 根据图1,从核属性集出发,采用自底向上的方法对属性约简的决策精度明显高于自顶向下式的约简.以Congressional Voting数据集为例,算法1的决策精度为0.632 2,0.613 5,0.609 5,0.609 0,0.627 4,0.632 7,0.625 2,0.622 8,0.634 4,0.606 9;算法2的决策精度为0.566 0,0.554 7,0.517 5,0.538 5,0.537 9,0.505 9,0.552 0,0.521 8,0.563 5,0.552 3.对比分析可以得到,从核属性集出发,采用自底向上的方法,通过每次加入一个重要度大的属性对属性进行约简,决策精度高. 为了对属性进行约简,文中首先研究知识之间的依赖关系.在基于容差关系的粗糙集模型中,研究了完全依赖、部分依赖及其依赖度等概念,接着探讨了不完备信息系统中知识依赖的性质,得到的结论用例子加以证明.接着对不完备信息系统的属性重要度进行了定义,提出了两个对属性进行约简的算法,算法1是一种启发式的约简算法,根据核属性进行约简.算法2从整个属性集出发,采用自顶向下的方法.通过实验证明,从核属性集出发,采用自底向上方法对属性约简,决策精度明显高于自顶向下式的约简. 对IIS中知识依赖的研究,使得知识依赖在不完备信息系统即遇到属性为空值的情况时,也能够具有新的合理解释并进行分析处理,从而为不完备信息系统中的属性约简提供新方法.今后还将进一步研究不完备信息系统中的粗糙集模型的扩展,以获得更多更好的粗糙集模型来处理不完备信息,提高其粗糙集的近似精度.5 求属性约简的启发式算法设计
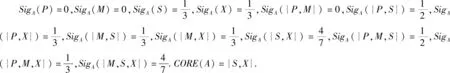
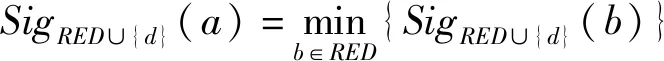
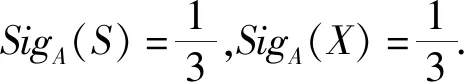

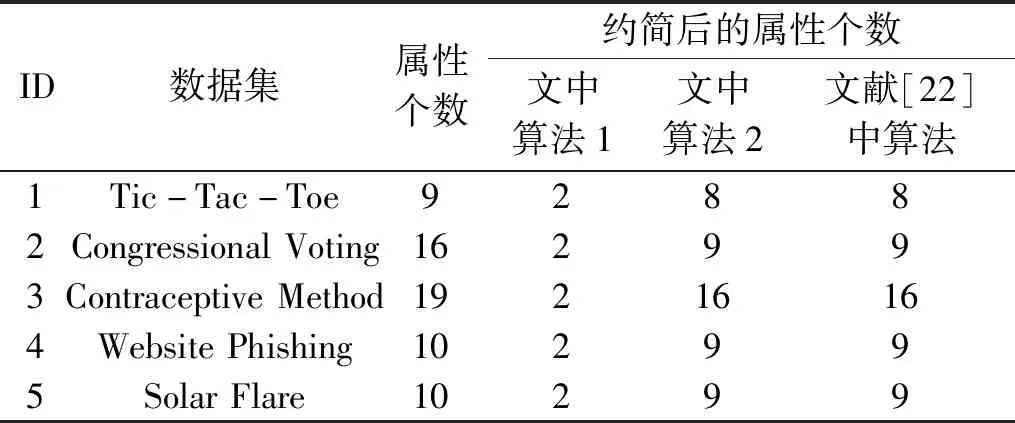
6 实验分析
6.1 结果对比
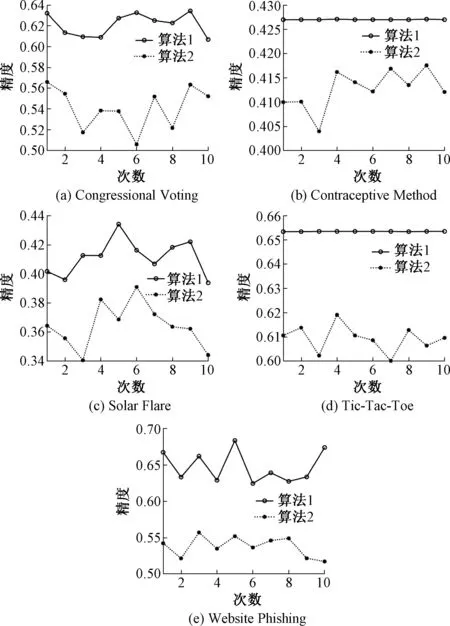
6.2 结果分析

7 结论
