基于BP神经网络的扇区空管运行亚健康关联因子预测

岳仁田，刘敬轩，赵嶷飞，肖瞳瞳，韩亚雄

(中国民航大学空中交通管理学院，天津 300300)

近年来，我国航空运输业呈现出高速发展的态势，随着交通需求的增长，空管系统经常以超负荷状态运行，虽然没有导致事故的发生，但不代表其状态是完全健康的。超负荷运行的空管系统实际上处于波动的亚健康状态，此时它的抗干扰能力和处理突发状况的能力下降，逐渐积累的安全隐患最终会导致事故的发生。因此，研究对空管运行亚健康状态进行科学评估的方法，从而采取预防亚健康状态向故障态转变的措施，对避免不安全事件的发生具有十分重要的意义，而空管运行亚健康状态评估和预测的首要一步是对空管运行亚健康关联因子进行预测。

目前，对空管运行状态安全风险的研究主要集中在空中交通流、空域容量参数以及空管运行安全风险评价体系等方面。如：2000年，Delahaye等[1]根据构建的扇区内交通流状态指标从几何学角度对空域拥挤状况进行了描述；2006年，Mulgund等[2]基于空中交通需求与空域容量的定量关系定义了“拥挤风险”的概念；2007年，Stamatelatos[3]利用贝叶斯定理，通过故障树建模和不确定分析对空管运行状态安全风险进行了评价和预测；2011年，Vismari等[4]运用流体随机Petri网对空中交通安全状态进行了评价；2013年，梁曼等[5]在分析空管人为因素时将组织因素纳入SHELL模型，组成SHELLO模型，并利用贝叶斯网络构建了事故的致因关系；2013年，张建平等[6]基于BP网络模型给出空管运行品质分类评价的人工智能方法，通过与主成分分析法的对比，说明了BP网络评价方法的评价效果相对更好；2014年，赵嶷飞等[7]通过建立占有因子、溢出因子、饱和因子三个描述性指标，对扇区空管运行状态进行了评估；2015年，Donald[8]采用内容分析、聚类分析和多元逻辑回归分析等方法，对影响空管安全的因素进行了研究；2015年，张兆宁等[9]运用耗散结构中的熵值理论研究了进近管制系统的风险性，证明了灰色关联熵能够揭示进近管制系统风险性增减变化的规律；2016年，张豫翔等[10]在模糊层次分析法的基础上结合云模型对空管迫降风险进行了评估；2018年，张亮[11]建立了管制扇区运行风险的博弈论集对(GT-SPA)耦合评价模型，对样本扇区安全运行风险等级进行了评估，提高了空管安全系统风险评估的准确性。

总体来说，国内外学者在空管运行状态安全风险评估方面进行了尝试并取得了阶段性的成果，但是由于空管系统的复杂性，目前的研究缺少对扇区空管运行状态的细致描述，未能有效结合空管运行过程中的关联因子，不能够体现事故征候前的临界时期。因此，本文根据空管运行状态影响因素的相互关系，构建了扇区繁忙时段BP神经网络预测模型，对扇区空管运行亚健康关联因子进行预测，并通过结果分析来判定扇区空管运行的状态。

1 扇区空管运行亚健康关联因子的提出及分类

空管系统运行由空中交通流、空中交通管制和外部资源环境等组成[12]，而扇区空管运行亚健康关联因子是与扇区空管运行状态转变有关的最基本要素。与安全风险因子相同，扇区空管运行亚健康关联因子从“人机环管”角度进行分类，可以反映扇区空管运行的状态，但是安全风险因子主要用来评估事故征候及事故发生时系统运行的状态，此时系统的故障程度已经较严重，而利用亚健康关联因子可以提早预测出系统发生故障的趋势，从而可以进行相应的调整，避免事故征候的发生。

扇区空管运行亚健康关联因子依托于空管运行大数据，包含交通流的空间时间分布、间隔状况、管制员工作负荷等具有内在关联性的指标，它们是通过提取区域管制的大量雷达数据，经计算得出的能够直观反映扇区空管运行状态的全新诊断指标，利用这些指标可以对扇区空管运行安全风险临界状态进行定性和定量研究。此外，针对表面单一风险因素致因事件，通过深层剖析亚健康关联因子间的相互关联性，可以准确预测风险。亚健康关联因子指标的选取是BP神经网络预测的基础，根据它们的类型可做如下分类：

空中交通流层面：航线交通量、航线交通特性(空间、时间分布不均衡度)、交通繁忙时段、交通流密度、航空器在扇区内的平均飞行时间……

空中交通管制层面：管制技能水平情况、工作负荷情况、管制间隔大小情况、与相邻管制单位移交协调情况……

外部资源环境层面：扇区形状、扇区结构、航路长度、地形及障碍物、导航设施工作状态、恶劣天气、军航活动……

由于亚健康关联因子分属反映扇区空管运行状态的不同层面，都具有一定的独立性，为了进行BP神经网络模型的应用，本文选取了部分有内在关联性的主要因素进行算例演示。

2 扇区空管运行亚健康关联因子指标选取及设计

2. 1 关联因子指标选取

短期内，扇区空中交通流在各航段分布的模式是保持不变的，其空间分布会直接影响到扇区空管运行的状态，而空中交通管制员是空管系统运行的核心，那么可以从空中交通流的空间分布和管制员工作两方面提取合适的指标，来进行扇区空管运行亚健康关联因子的计算。管制员工作负荷是扇区空管运行状态人为影响因素中的关键组成部分，可以作为扇区空管运行亚健康关联因子预测的指标，而扇区内管制员的工作负荷受交通量空间、时间分布的直接影响，亚健康关联因子中衡量交通量空间、时间分布且具有内在关联性的主要指标有航空器平均飞行时间、交通流超容比、交通流空间分布不均衡度、交通流瞬时超容率，它们在研究时段内变化大、易于统计和计算，因此可以选择这些亚键康关联因子指标对管制员工作负荷进行预测。

2. 2 关联因子指标设计

2.2.1 交通流超容比

空中交通流在扇区内的繁忙情况可以通过计算超容比来定义。超容比能够反映交通流在时间片内的变化，它是指扇区内超过其运行容量的航班服务架次占运行容量的比率[13]，其计算公式如下：

(1)

式中:R为交通流超容比(无量纲);Q为扇区的航班服务架次(架)；P为扇区运行容量(架)。

2.2.2 交通流空间分布不均衡度

扇区空中交通流的空间分布均匀程度直接影响空管系统运行的品质，因此交通流空间分布不均衡度能够作为扇区亚健康关联因子预测研究的重要指标，它是指单位时间内不同航段个体之间所服务航班架次的差异，可以利用基尼系数进行定量表示[13]。基尼系数是判断分配平等程度的指标，该指标由洛伦茨曲线(见图1)可以推导得到，其计算公式如下：

(2)

式中：G为基尼系数；A为洛伦茨曲线和绝对平均线(45°线)之间的区域面积；B为洛伦茨曲线以下的区域面积。

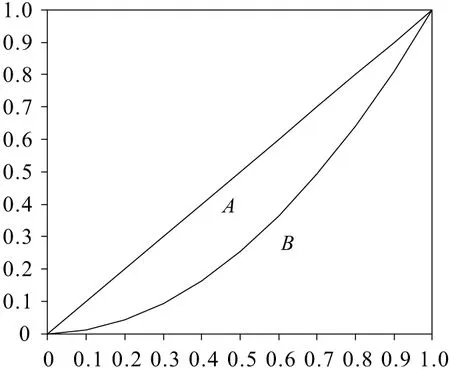
图1 洛伦茨曲线Fig.1 Lorentz curves

图1中，若A为0，则基尼系数为0，表示交通流空间分布完全均衡；若B为0，则基尼系数为1，表示交通流空间分布绝对不均衡，即完全失调。交通流空间分布越是趋向均衡，洛伦茨曲线的弧度越小，基尼系数也越小；反之，交通流空间分布越是趋向失调，洛伦茨曲线的弧度越大，基尼系数也越大。本文以扇区内航班服务架次累计百分比作为纵坐标，以航路里程累计百分比作为横坐标，运用Matlab软件计算各时间片内的基尼系数。

2.2.3 交通流瞬时超容率

扇区空中交通流的微观特性可以通过计算其瞬时超容比来进行定量分析，它能够实时地反映单位时间内扇区空管运行的状态：若交通流瞬时超容比的值大于0，则单位时间内的扇区流量超容。本文以15 min作为一个时间片进行研究，交通流瞬时超容比大于0的分钟数占研究区间的比例越大，即瞬时超容率越大，说明扇区空管运行状态越差。交通流瞬时超容率指标的计算公式如下：

(3)

(4)

式中:Si为第imin的瞬时超容比(无量纲)，i=1,2,…,15;Qi为第imin航班服务架次(架)，i=1,2,…,15;QMAP为与监控警告参数MAP数值相等的扇区容量(架)；l为交通流瞬时超容率(无量纲)；j为交通流瞬时超容比大于0的分钟数(min)。

其中，监控警告参数(MAP)的计算公式如下：

(5)

式中:T为航空器扇区平均飞行时间(min);τ为单位时间管制员工作负荷(min),本文暂取人为因素专家制定的数值，即0.6 min。

2.2.4 管制员工作负荷

管制员工作负荷是扇区空管运行呈亚健康状态的主要致因成分，因此可以作为扇区空管运行亚健康关联因子预测的指标。管制员工作负荷分为看得见的负荷和看不见的负荷，在此主要研究看得见的负荷。本文将管制员工作负荷定义为管制通话时间和设备操作时间的总和[14]。此外，本文选取相关研究建立完成的厦门1号扇区的管制员工作负荷模型进行管制员工作负荷指标运算[15]，其计算公式如下：

W=0.057Q3-2.604Q2+53.73Q-52.76

(6)

式中:W为管制员工作负荷(s)；Q为时间片内扇区航班服务架次(架)。

时间片内每架航空器平均管制工作负荷计算公式如下：

(7)

3 扇区空管运行亚健康关联因子的BP神经网络预测模型构建

BP(Back Propagation)神经网络可以学习和储存大量输入-输出模式映射关系，且不需要事前揭示描述这种映射关系的数学方程，因此根据扇区特点及空管运行情况，在分析扇区空管运行亚健康关联因子之间关系的基础上，通过建立完整的BP神经网络，可以进行较高精度的预测研究。扇区空管运行亚健康关联因子的BP神经网络预测模型的构建主要包括以下6个步骤[16]：

(1) 样本数据归一化处理。扇区空管亚健康关联因子各指标具有不同的量纲和单位，会导致BP神经网络收敛速度慢，训练时间延长，从而影响数据分析的结果。为了解决数据指标之间的可比性，需要对所有样本数据进行归一化处理。通常采用最大-最小标准化算法将数据进行归一化处理，把原始值映射到特定区间内，其计算公式如下：

(8)

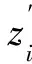
(2) 网络初始化。选取指标作为网络结构的输入与输出，若有n个输入指标、m个输出指标，则输入层神经元节点数为n、输出层神经元节点数为m。隐含层神经元节点数根据以下常用的经验公式得到：

(9)

式中:n为输入层神经元节点数；m为输出层神经元节点数;p为隐含层神经元节点数;a为[1,10]之间的常数。

(3) 训练参数的设定。为了提高BP神经网络的预测精度，需要设置合适的训练参数，常用的训练参数有最大迭代次数、学习速率、训练要求精度、动量系数、动态参数等。

(4) 隐含层传递函数的选择。BP神经网络一般使用Sigmoid函数或线性函数作为传递函数，Sigmoid函数根据输出值的取值范围分为对数S型函数(Log-sigmoid)和双曲正切S型函数(Tan-sigmoid)，它们分别可由如下公式确定：

(10)

(11)

(5) 网络训练。对归一化后的输入样本矢量集、目标样本矢量集进行网络训练。

(6) 网络仿真。将需要预测的目标数据放入到训练成功的神经网络中，输出预测结果。

4 实例验证与分析

4. 1 数据来源

为了直观地展现扇区亚健康关联因子的预测过程，本文利用厦门1号扇区2013年10月1日08∶00—13∶00时段的实际运行雷达数据进行相关运算，已知厦门1号扇区公布的运行容量为11架次/15 min，同时为了精确统计扇区航班服务架次、航空器扇区平均飞行时间，所以将15 min作为一个时间片进行研究。在2013年10月1日11∶15—11∶30时间片内，航班流量为6架/15 min，未达到运行容量，为保证计算精度，剔除这一时段数据，对剩余19个时间片进行研究，见表1。

表1 厦门1号扇区部分统计数据

4. 2 扇区关联因子指标计算

本文利用表1中厦门1号扇区的数据，根据公式(1)～(7)计算各时间片内该扇区亚健康关联因子指标的数值，即交通流超容比、交通流空间分布不均衡度、交通流瞬时超容率、每架航空器平均管制工作负荷，其计算结果见表2。

表2 各时间片内厦门1号扇区亚健康关联因子指标 计算结果

4.3 基于BP神经网络模型的扇区亚健康关联因子预测

4.3.1 数据归一化处理

本文将表2中的厦门1号扇区相关指标的计算结果采用最大-最小标准化算法进行归一化处理，以08∶15—08∶30时间片中的航空器扇区平行飞行时间(T=7 min)为例，所有时间片中10∶15—10∶30的航空器扇区平均飞行时间数值最大，时间片12∶00—12∶15的数值最小，即Tmax=9 min，Tmin=4 min，而T=7 min，那么T′=(7-4)/(9-4)=0.6。所有时间片该扇区相关指标的归一化处理结果见表3。

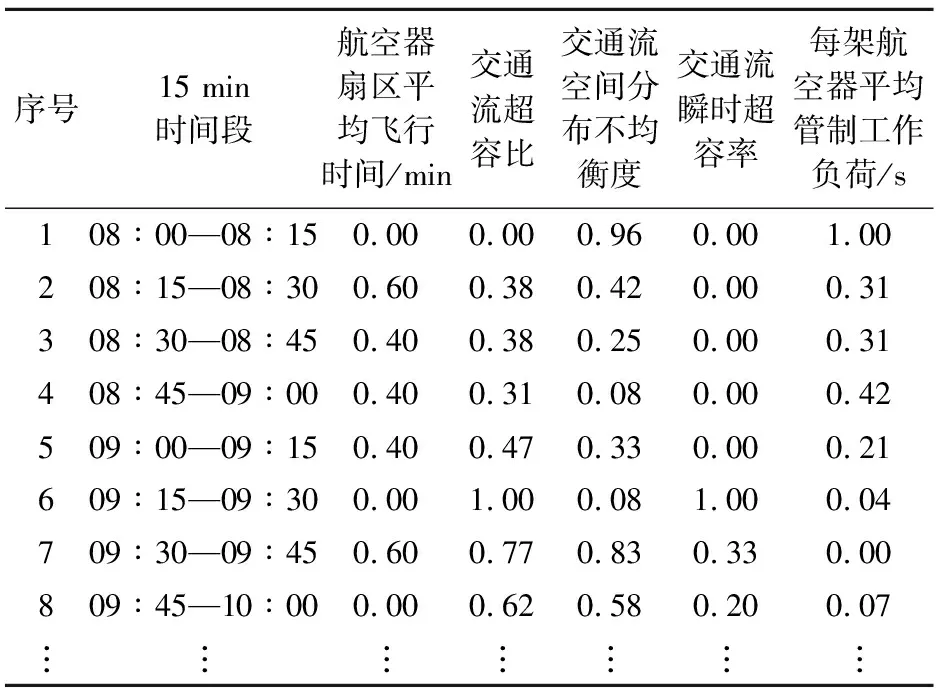
表3 各时间片内厦门1号扇区亚健康关联因子指标 归一化处理结果

4.3.2 BP神经网络预测

本文将表3中的厦门1号扇区相关指标归一化处理结果作为BP神经网络模型的输入数据。以每架航空器平均管制工作负荷作为果变量y，航空器扇区平均飞行时间、交通流超容比、交通流空间分布不均衡度、交通流瞬时超容率构成因变量集合{x1,x2,x3,x4}，运用BP神经网络进行扇区空管运行亚健康关联因子预测。因变量集合中有4个指标，则输入层神经元节点数为4；果变量只有一个指标，则输出层神经元节点数为1；由公式(9)计算得出隐含层神经元节点数在4至13之间，最终由实验法选择最佳隐含层神经元节点数为7。以三隐含层BP神经网络进行扇区空管运行亚健康关联因子预测模型的构建，得到三隐含层4×7×1 BP神经网络结构预测模型，见图2。

图2 三隐含层BP神经网络结构预测模型Fig.2 Prediction model of BP neural network with three hidden layers

将表3中前15组的归一化后数据输入BP神经网络，训练形成稳定的模型结构，并设定网络隐含层激励函数为双曲正切S型函数(Tan-sigmoid)，输出层激励函数为线性函数，网络训练函数为traingdx，网络性能函数为mse。设置网络参数：网络迭代次数epochs为5 000次，期望误差goal为0.000 01，学习速率lr为0.01。

从表3中选取第16至18组的归一化后数据作为验证数据，分析BP神经网络模型预测结果的误差精度，并利用Matlab程序对训练好的BP神经网络模型进行分析计算，将得到的三个时间片的预测结果进行反归一化，其结果见表4。

表4 BP神经网络的预测结果和预测误差

由表4可知，BP神经网络模型的预测值与实际值的相对误差低于3%，说明该BP神经网络模型可以满足扇区空管运行亚健康关联因子预测的应用要求。

对表3中最后一组数据进行BP神经网络模拟仿真，其网络训练误差结果见图3。

图3 BP神经网络训练误差结果图Fig.3 Training error result of the BP neural network

由图3可见，BP神经网络经过约133步的训练模拟达到设定的精度要求0.000 01，说明该网络收敛速度较快。

4.3.3 结果分析与讨论

BP神经网络模拟的输出结果显示第19组数据12∶45—13∶00时间片的预测值为0.48，反归一化得到预测值为24.32，即每架航空器平均管制工作负荷是24.32 s。相关研究表明，基于管制员工作负荷的容量评估中负荷阈值的取值范围为60%～80%，超过该范围，空域碰撞风险水平急剧上升[15]，所以每架航空器平均管制工作负荷必须小于最高负荷的80%。管制负荷百分比的计算公式如下：

(12)

式中:ω为管制负荷百分比(%)；Wmax为管制员最高工作负荷(s)。

经过多位专家分析评定，管制负荷百分比在55%以下时，管制员工作压力较小而感到轻松；管制负荷百分比在55%～65%时，管制员感受到压力但能保持常态化工作状态；当大量航班进入扇区，管制员感到较大压力，管制负荷百分比在65%～75%时，此时若还存在交叉、汇聚趋势的特殊运行航班，管制员的紧张度增加；管制负荷百分比在75%以上时，管制员高度紧张，事故征侯发生。因此，根据管制负荷百分比的数值可将扇区空管运行状态预警等级设定为4级，见表5。

表5 扇区空管运行状态预警等级

已知在12∶59—13∶00时间片中扇区航班服务数量为7架次，是第19组时间片内的最大值，此时管制员工作负荷最高，由公式(6)计算得出管制员最高工作负荷为215.31 s。因此，预测得到的每架航空器平均管制工作负荷占管制员最高负荷的百分比由公式(12)计算得到结果为11.30%，在55%以下，认为这一时间段内扇区空管运行处于健康状态，不需要采取措施进行干预。扇区空管运行状态在预警等级Ⅱ时，也可以不采取预控措施，但应引起注意，防止亚健康状态向故障态变化。当扇区空管运行状态在预警等级Ⅲ、Ⅳ时，应采取相应的措施，如：发布流量控制通知，限制其他航班进入扇区；进行换岗，严格调整执勤人数和时间；当有恶劣天气等特殊情况出现，应请求带班主任的帮助。

5 结 论

本文从各层面考虑了各类型的扇区空管运行亚健康关联因子，从中选取有内在联系的客观性指标进行BP神经网络的预测，消除了主观赋值的误差。对厦门1号扇区空中交通流实际运行雷达数据进行了标准化处理，消除了指标间的量纲影响，有助于提高BP神经网络运算的准确性。构建的三隐含层BP神经网络结构预测模型经实例检验能够真实地反映扇区的运行状态，表明该模型在实际应用中具有可行性。

扇区空管运行亚健康关联因子的预测能够针对空中交通流的微观特性、管制员工作负荷等方面进行定性和定量的研究，为扇区空管运行状态的预估奠定了基础，有利于将亚健康理论应用到空管安全管理中，实现由事后调查处理向事前预警防范的转变。