基于岩石损伤与水力作用的顺层岩质边坡临界失稳高度研究

张勃成，唐辉明,2，申培武，宁奕冰，夏 丁

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.中国地质大学(武汉)教育部三峡地质灾害研究中心，湖北 武汉430074)

岩质边坡尤其是顺层岩质边坡是目前工程建设中最为常见的一类边坡，该类边坡失稳破坏往往会造成严重的人员伤亡和巨大的经济损失，同时也会影响通信、交通运输、基础设施和公共设施等，造成不良的社会影响[1-2]。如：1999年11月12日京珠高速公路韶关段边坡发生顺层滑动，延长工期15天[3]；2004年9月5日重庆万州吉安发生滑坡，滑坡摧毁了当地一个重要集镇、公路和在建的高速公路[4]；2009年6月5日重庆市武隆县铁矿乡鸡尾山山体发生大规模的崩滑破坏，造成10人死亡、64人失踪[5]；等等。有研究[6-7]认为，顺层岩质边坡的稳定性与边坡倾角、岩层倾角、地表水、地下水、降雨和人为活动有关，其中内控因素主要是边坡几何特征和地下水系统，诱发因素为降雨和人为活动等。当顺层岩质边坡满足一定的地质条件并在人类工程活动的影响下，由层状沉积岩和变质沉积岩形成的斜坡就会发生平面破坏[1,8]。基于平面破坏模式的顺层岩质边坡的失稳破坏研究已经引起众多学者的关注[1]，然而由于岩体本身存在断层、节理、层理等不连续面，使得顺层岩质边坡的稳定性评价变得较为困难。

尽管如此，顺层岩质边坡的稳定性问题仍是工程界较为关注的研究领域，不少学者从不同角度对该类边坡的破坏机理进行了较为深入的研究，并提出了多种边坡稳定性分析方法[9-15]。一般而言，顺层岩质边坡稳定性分析方法主要有常规方法、数值模拟方法和原位模型试验方法。近年来，数值模拟方法和原位模型试验方法已经成为分析顺层岩质边坡破坏过程及失稳稳定性评价的重要手段。如殷跃平[16]以重庆武隆鸡尾山滑坡为例，利用FLAC3D软件模拟分析了斜厚层山体倾滑坡脆性剪断的视向滑动破坏特征、由真倾向滑移变形转为视倾向整体滑动的变形破坏模式，并提出了斜倾厚层山体滑坡视向滑动具备的条件；葛云峰等[17]利用大型三维离散元软件3DEC，对武隆鸡尾山滑坡滑动面力学参数对滑坡稳定性的影响进行了模拟研究。虽然数值模拟方法和原位模型试验方法已成为顺层岩质边坡稳定性分析的热门方法，但常规方法如运动学分析法、极限平衡分析法、概率分析法仍然是顺层岩质边坡稳定性分析的主要手段。如Zanbak[18]、Sagaseta等[19]、Amini等[20]众多学者讨论并改进了极限平衡分析法，使得其在顺层岩质边坡稳定性分析和实际边坡设计中发挥着日益重要的作用。然而当岩层长度、倾角和受力方向满足一定条件时，岩质边坡的失稳破坏模式会发生改变，如较高的直立岩质边坡受到的荷载主要为自重，此时岩层产生特有的破坏模式。张天军等[10]在考虑岩石流变性的基础上采用自重作用下的梁柱力学模型对直立层状岩质边坡倾倒破坏进行了分析，并得出了直立层状岩质边坡临界失稳高度的求解方法；肖树芳等[9]采用欧拉压杆稳定力学模型对直立层状岩质边坡溃屈失稳破坏进行了分析，也得出了直立层状岩质边坡临界失稳高度的计算公式。

不少学者已经基于欧拉压杆理论对层状岩质边坡溃屈失稳破坏进行了研究，但现有研究中仍然存在如下问题：①现有研究中基本都是基于直立层状岩质边坡建立失稳破坏模型，对顺层岩质边坡的研究较少；②在考虑边坡失稳破坏模型时，大多数是基于边坡的几何特征建立的力学模型，没有考虑地下水这一诱发因素；③目前建立的顺层岩质边坡失稳破坏模型大多数是将岩石看作完整无损伤的地质材料，然而岩石是内部存在损伤的非均匀地质材料。基于现有研究中存在的问题，本文在前人研究的基础上，首先建立了考虑水力作用的顺层岩质边坡临界失稳高度的计算模型，并对其进行了验证分析；然后将岩石看成是微元强度服从正态分布的损伤地质材料，建立了考虑水力作用与岩石损伤的顺层岩质边坡临界失稳高度的计算模型；最后结合具体工程实例对建立的模型进行验证，证明将岩石看作为损伤地质材料而建立的顺层岩质边坡临界失稳高度的计算模型具有一定的可靠性和可行性。

1 直立层状岩质边坡的欧拉压杆失稳破坏模型

压杆稳定性问题在材料力学中较为常见，常将研究对象看作不同杆端约束下的细长中心受压直杆。在建立中心受压杆件稳定性计算公式前，常做如下假设：①杆件长度远远大于其宽度；②忽略压杆自身重量；③杆件材料处于理想线弹性范围内，即杆件只发生弹性失稳。基于上述假设，推导出细长中心受压等直杆临界力的欧拉公式为

Pcr=π2EI/(μl)2

(1)

式中：Pcr为受压杆件临界力(N)；E为杆件材料的弹性模量(Pa)；I为横截面惯性矩(m4)，杆端约束情况相同时，其采用最小形心主惯性矩；μ为压杆的长度因数(无量纲)，与杆端的约束情况有关；l为杆件长度(m)。

直立层状岩层边坡在一定高度下会发生溃屈破坏，当岩层长度远大于宽度时，该岩层可以看作细长直杆，其破坏类型类似于压杆失稳破坏。目前，一些学者已经将欧拉压杆理论应用到直立岩层中，如刘红岩等[21]研究认为将竖直岩层自重当作集中荷载作用在杆端与竖直岩层实际受力情况不符，并提出了一种直立岩层在自重作用下的失稳力学模型。由于该模型能更好地符合直立层状岩质边坡的实际受力特征和破坏情况，所以本文直接采用其研究成果，则该模型下的直立岩层的临界失稳高度为

(2)

式中：l为直立岩层高度(m)；q为岩层自重荷载(N/m2)，q=γt，其中γ为岩石材料密度(N/m3)，t为岩层厚度(m)；I为横截面惯性矩(m4)，I=bh3/12，其中b为横截面长边(m)，h为横截面短边(m)，由于考虑问题为平面问题，垂直于截面的延伸长度取值为1 m，若杆端约束情况相同，则取最小惯性矩。

2 顺层岩质边坡的欧拉压杆失稳破坏模型

顺层岩质边坡在实际工程案例中比直立层状岩质边坡更为常见，为了扩大欧拉压杆失稳理论在边坡领域中的应用，将上述直立层状岩质边坡的欧拉压杆失稳破坏模型的建模思想推广到顺层岩质边坡的欧拉压杆失稳破坏模型的建模过程中。

2. 1 考虑水力作用的顺层岩质边坡受力分析

地下水是影响边坡稳定性的重要因素之一，坡体地下水对边坡作用力的类型分为静水压力效应、浮托力效应、滑带土饱和软化效应和渗透压力效应[22-24]。由于顺层岩质边坡的特殊性，使得地下水在该类型滑坡中的作用主要为边坡滑动面上的拖拽力、扬压力以及坡体后缘的裂隙水压力，见图1。

(1) 拖拽力。拖拽力指的是地下水在边坡滑动面上流动时地下水的渗透压力对坡体产生的力的作用，主要由地下水的渗透作用转化而来。拖拽力的大小和方向与地下水在边坡滑动面上的水力梯度分布有关。在顺层岩质边坡稳定性评价研究中，常认为地下水在边坡滑动面上的运动规律符合达西定律，即地下水渗透压力与水力梯度呈线性关系分布。在岩质边坡稳定性评价过程中，无论结构面中是否存在填充层，地下水均会在结构面壁上产生拖拽力，但是目前精确计算拖拽力的大小存在着一定的困难，考虑到拖拽力在结构上下面均有分布，可认为地下水对边坡层面上部岩体的拖拽力为总拖拽力的一半，则地下水在边坡结构面的拖拽力计算公式为[23]

j=1/2bγwi

(3)

式中：j为地下水在边坡结构面上单位长度的拖拽力(N/m)；b为边坡结构面开度(无量纲)；γw为水的重度(N/m3)；i为边坡结构面处的水力梯度(m)，在本模型中取值与坡体后缘裂隙深度相等。

(2) 扬压力。扬压力指的是地下水上升产生的静水压力对上覆不透水岩层的作用，由于扬压力的存在能够有效降低坡体支持力，所以扬压力也是导致边坡失稳的一个重要影响因素，则边坡滑动面上的扬压力计算公式为[23]

P1=1/2γwHL

(4)

式中：P1为地下水在边坡结构面上的扬压力(N)；L为边坡滑动面长度(m)；H为坡体后缘张裂隙充水高度(m)。

(3) 坡体后缘裂隙水压力。坡体后缘裂隙水压力指的是坡体后缘张裂隙充水后，张裂隙的静水压力对坡体产生的力的作用。坡体后缘裂隙静水压力主要会对坡体产生两种不利作用：一是静水压力垂直作用在边坡滑动面上的分量降低了坡体有效应力，减少了滑坡的抗滑力；二是静水压力平行作用于边坡滑动面上的分量直接增加坡体的下滑力。则坡体后缘裂隙水压力计算公式为[23]

P2=1/2γwH2

(5)

式中：P2为坡体后缘裂隙水压力(N)；γw为水的重度(N/m3)；H为坡体后缘张裂隙充水高度(m)。

通过上面公式可知，地下水对顺层岩质边坡的作用力大小与坡体后缘张裂隙的充水高度密切相关，故坡体后缘张裂隙的充水高度是顺层岩质稳定性的重要参数。

2.2 考虑水力作用的顺层岩质边坡失稳破坏模型

岩质边坡破坏的模式有很多，平面滑动破坏是顺层岩质边坡破坏模式中较为常见的一种，该类边坡滑动面常常为软弱结构面，坡体前缘存在侧向临空面、软弱结构面、侧向临空面以及坡体后缘近乎贯通的垂直张裂隙形成控制顺层岩质边坡稳定性的控稳优势结构面，在水的作用下诱发边坡发生失稳破坏。基于上述分析，做出如下假设：①边坡滑动面为岩层层面；②坡体后缘张裂隙垂直，地下水可以从后缘张裂隙沿着滑动面流动并从坡体前缘流出；③由于边坡发生滑动，黏结力不予考虑；④降雨完全充满后缘张裂隙。建立考虑水力作用的顺层岩质边坡失稳破坏模型需要考虑坡体自身重力、岩层层间摩擦阻力和下伏岩层支持力。通过以上条件建立的顺层岩质边坡受力模型见图2。

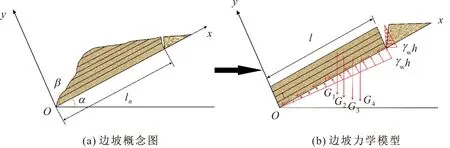
图2 顺层岩质边坡受力模型Fig.2 Mechanical model of bedding rock slope

第一层岩层沿x轴方向受到的力为

Pc1=G1sinα+P2-1cosα-(G1cosα-P2-1sinα)tanφ1

(6)

式中：Pc1为第一层岩层沿着层面受到的力；P2-1为坡体后缘张裂隙水压力作用在第一层岩层上的力。

第二层岩层沿x轴方向受到的力为

(7)

第k层岩层沿x轴方向受到的力为

(8)

由于要考虑到地下水扬压力和拖拽力的作用，则第n层岩层沿x轴方向受到的力为

(9)

将上述公式中各层岩层沿x轴方向受到的力相加，得到整个滑坡体沿x轴方向受到的力为

(10)

假设该滑坡共有n层岩层发生整体失稳破坏，可将整个顺倾岩质边坡视为一个杆件，该边坡的整体失稳破坏极限长度为l，假设该边坡岩体弹性模量均相等，令Pcr=Psum，则可以计算出整个滑坡体的临界失稳高度为

(11)

引用文献[25]中岩石材料参数，即取E=65 GPa、γ=26 000 N/m3、t=1 m、α=35°、φ=30°，由公式(11)可计算得到顺层岩质边坡的临界失稳高度为207.08 m，而在不考虑地下水作用下求得的顺层岩质边坡的临界失稳高度为256.55 m。通过对比发现，考虑地下水作用的顺层岩质边坡的临界失稳高度是不考虑地下水作用的80.71%，因此考虑地下水作用得到的计算结果更加危险，表明地下水作用使边坡失稳的可能性大大增加。

将本文建立的考虑水力作用的顺层岩质边坡失稳破坏模型与文献[9]建立的模型进行了对比分析，利用文献[9]推导出的公式计算出不考虑地下水作用的顺层岩质边坡临界失稳高度为344.43 m，而考虑地下水作用的顺层岩质边坡临界失稳高度约是不考虑地下水作用的60.12%，其主要原因是将呈线性分布的荷载作为集中荷载施加在岩层顶端以及未考虑地下水作用，故利用本文建立的顺层岩质边坡失稳破坏模型进行工程施工设计，可使得工程更加偏于安全。

对于顺层岩质边坡而言，仍沿用上面参数并采用固定其他参数改变一个参数的研究方法，开展顺层岩质边坡临界失稳高度随岩层倾角α和内摩擦角φ的变化规律研究，得到顺层岩质边坡临界失稳高度随岩层倾角α和内摩擦角φ的变化规律，见图3。

图3 顺层岩质边坡临界失稳高度与岩层倾角和内摩 擦角的关系曲线Fig.3 Relation curve between the critical instability height and the strate dip angle and inner friction

由图3可见，当模型其他参数不变时，随着顺层岩质边坡岩层倾角的增加，边坡临界失稳高度减小，且当岩层倾角较小时，边坡临界失稳高度减小较为剧烈；随着顺层岩质边坡岩层内摩擦角的增加，边坡临界失稳高度增加，当岩层内摩擦角增加到一定值时，边坡临界失稳高度明显增加，即岩层内摩擦角增加使得滑坡更加稳定。

2.3 考虑水力作用与岩石损伤的顺层岩质边坡失稳破坏模型

岩石材料是极其复杂的非连续和非均质岩体，宏观上完整岩石实际上也是一种自带损伤的地质材料，其内部或多或少分布着微裂隙[26]。岩石变形破坏过程实际上也是微裂隙萌生、发展、演化到宏观裂隙产生、断裂、贯通的全过程。就目前而言，许多学者从岩石材料内部所含缺陷分布的随机性出发，将连续损伤力学和统计学方法结合起来，从岩石微元强度服从某种随机分布的角度，建立了岩石损伤本构方程，进一步推动了岩石损伤力学的发展。目前的研究均是从岩石微元强度服从正态分布、类Weibull分布和Weibull分布出发，建立岩石损伤本构模型。如曹文贵等[27]引入岩石微元强度服从正态分布的概念，建立了岩石损伤本构模型，考虑到建立模型只反映某一特定围压下岩石破裂过程的统计损伤演化关系，故对该模型参数进行了修正，建立了能够反映不同围压或者不同的复杂应力状态下的岩石损伤模型，使得修正后所得到的模型更加接近实际。就应用范围而言，正态分布、类Weibull分布和Weibull分布均能较好地反映脆性材料，正态分布和Weibull分布也适用于准脆性材料，但是考虑到正态分布模型参数简单，可通过单轴或简单三轴试验拟合来确定[27-28]。因此，本文采用基于对正态分布的岩石损伤模型进行研究较为合理。

基于Drucker-Prager破坏准则的岩石微元强度F可表示为

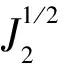
(12)

假设岩石的微元强度F服从对数正态分布，其概率密度函数为

(13)

式中：F0、S0为正态分布参数，其中F0反映了岩石峰值强度大小，S0反映了岩石的脆性特征，可通过三轴应力-应变试验曲线拟合来确定。

岩石的损伤变量可表示为

(14)

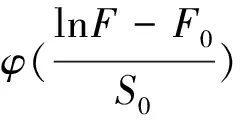
根据J.Lemaitre的应变等效性假设，建立岩石损伤本构关系如下:

[σ*]=[σ]/(1-D)

(15)

式中：[σ*]为有效应力矩阵；[σ]为总应力矩阵；D为岩石损伤变量。

假定岩石微元在破坏前服从广义虎克定律,则：

(16)

联立公式(15)和(16),可得：

σ1=Eε1[1-D]+μ(σ2+σ3)

(17)

将岩石材料看作均匀材料建立的顺层岩质边坡失稳破坏模型与实际情况存在差异，本文以岩石损伤模型为基础，重新建立顺层岩质边坡失稳破坏模型。通过公式(17)可以看出，岩石损伤主要体现在岩石弹性模量的弱化，所以将公式(14)代入公式(11)中，得到将岩石材料视为损伤材料的顺层岩质边坡的临界失稳高度计算公式如下：

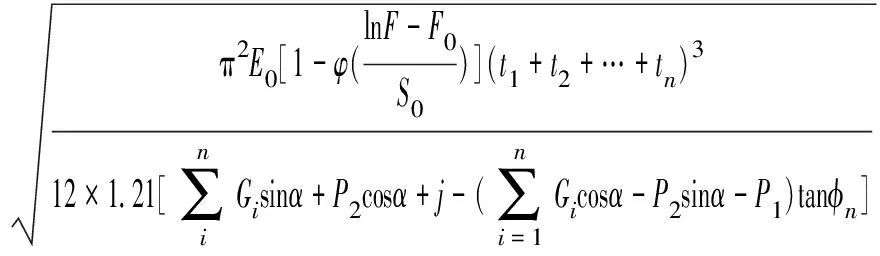
(18)

为了验证岩石损伤对顺层岩质边坡的临界失稳高度的影响，引用文献[27]中的岩石材料参数，即取ε1=1 mm、μ=0.3、σc=110 MPa、σ1=60 MPa、σ3=10 MPa、E=65 GPa，顺层岩质边坡仍然采用前述参数，即γ=26 000 N/m3、t=1 m、α=35°、φ=30°，利用公式(14)，即求得岩石初始损伤变量为0.169 23，将其代入公式(18)可计算得到考虑岩石损伤的顺层岩质边坡临界失稳高度为194.63 m。而未考虑岩石损伤的顺层岩质边坡临界失稳高度为207.08 m，两者差值占考虑岩石损伤的顺层岩质边坡临界失稳高度的6.02%，且考虑岩石损伤的顺层岩质边坡临界失稳高度小于不考虑岩石体损伤的顺层岩质边坡临界失稳高度，说明本文建立的考虑岩石损伤的顺层岩质边坡失稳破坏模型具有一定的可行性。为了更好地反映岩石材料的力学行为，在计算时应根据具体工程条件和岩体材料特征，将岩石损伤考虑在边坡失稳破坏模型中，以期更加符合工程实际。

3 工程实例验证

本文结合具体工程实例对上述建立的考虑水力作用与岩石损伤的顺层岩质边坡失稳破坏模型的可行性进行了验证。

3. 1 案例一

以文献[29]中贵阳西二环“5·20”滑坡为例，该滑坡区位于贵阳西侧市政道路西二环北段与北二环的交叉处，微地貌单元主要表现为低山丘陵，地势北高南低的凸型山脊由西北向南东展布，自然斜坡未滑动前的原始坡度约为17°～27°，地层呈单斜构造，岩层产状为140°∠25°。该滑坡前缘高程为1 270.10～1 272.16 m，后缘高程为1 344.79 m;滑坡距离路面垂直高度最大值为74.50 m，横向平均宽度约为78.00 m，纵向平均长度约为126.00 m；滑体平均厚度约为5.6 m，平面面积约为16 908.73 m2，体积约为5.503×104m3；滑坡主滑方向为138°。滑坡区构造简单，岩体节理裂隙发育，节理面为软弱结构面，结构面结合程度差，较为光滑，层面岩屑夹泥充填。

该滑坡为中型顺层牵引式滑坡，该滑坡平面形态与原始地形较为相似，总体上呈长舌状。滑坡体主要由强风化白云岩、中风化白云岩、角砾状白云岩构成，还有少量第四系含碎石耕植土；滑带物质主要是为含砾黏土，呈浅黄-灰黄色，稍密状态，滑带土总体结构松散、杂乱，具有较好的透水性，滑带土厚约10～35 mm，力学性质极差，多处可见擦痕，局部滑面可见少量潜水渗出；滑床为灰色中风化白云岩、角砾状白云岩，节理裂隙较为发育，擦痕方向与主滑方向一致，滑面整体平直。结合地质环境条件和滑坡变形破坏特征建立滑面形态，并得到该滑坡典型地质剖面图,见图4。

由文献[29]可知,天然状态下岩石材料基本参数取值为γ=26 200 N/m3、α=25°、φ=14.1°，t=5.6 m；饱和状态下岩石材料基本参数取值为γ=27 800 N/m3、α=25°、φ=13.1°，t=5.6 m；白云岩弹性模量按照推荐值取值为20～40 GPa[30]。在天然状态不考虑地下水作用的情况下，将上述参数取值代入公式[18]中，可以定量计算出该滑坡的临界失稳高度为138.58～174.59 m；在饱和状态考虑地下水作用的情况下，将上述参数取值代入公式[18]中，可以定量计算出该滑坡的临界失稳高度为123.95～156.51 m。根据相关资料可知，该滑坡发生滑动的纵向长度约为126 m，假设白云岩弹性模量取值为E=20 GPa，天然状态下计算出的滑坡临界失稳高度为138.58 m，降雨状态下计算出的滑坡临界失稳高度为123.95 m，说明该滑坡在天然状态下处于稳定状态，在降雨条件下由于滑坡体的内摩擦角减小、重度增加以及地下水作用降低了滑坡的稳定性，使得该滑坡更容易发生失稳滑动；假设白云岩弹性模量取值为E=40 GPa，天然状态下计算出的滑坡临界失稳高度为174.59 m，降雨状态下计算出的滑坡临界失稳高度为156.51 m，虽然降雨明显降低了滑坡的稳定性，但是滑坡仍处于稳定状态。通过对比不同岩石弹性模量计算出的滑坡临界失稳高度，说明岩石弹性模量的弱化会导致滑坡稳定性降低，也进一步说明岩石风化是导致该滑坡失稳破坏的一个诱发因素。此外，通过分析可知，天然状态下计算出的滑坡临界失稳高度与暴雨条件下计算出的滑坡临界失稳高度的差值占暴雨条件下计算出的滑坡临界失稳高度的11.5%～11.8%，说明降雨也是导致该滑坡失稳破坏的一个重要诱发因素，这与该滑坡在暴雨条件下发生失稳破坏的实际情况一致。

3. 2 案例二

以文献[31]中位于重庆市南岸区人工开挖的顺层岩质边坡为例，该边坡坡体主要由侏罗系中统新田沟组页岩组成，坡脚有部分砂岩，岩层倾向坡体临空面，岩层产状为291°∠71°，边坡内部发育有结构面，岩石完整性较差。该边坡采用锚杆挡墙支护，在边开挖边支护的过程中，边坡开挖高度接近35 m时，边坡发生了失稳破坏，该边坡典型地质剖面见图5。

由文献[31]可知,岩石材料基本参数取值为E=1.187 GPa、γ=24 640 N/m3、α=71°、φ=30°，由于失稳岩体水平宽度为5.0 m，所以岩体厚度t的取值为4.73 m。将上述参数取值代入公式[18]中，在不考虑岩石损伤情况下，可以定量计算出该边坡的临界失稳高度为34.5 m，而在不考虑地下水作用的情况下边坡临界失稳高度为35.1 m。根据勘察资料可知，该边坡溃屈破坏顶面与地面的最高高差为36.45 m，计算得到的边坡临界失稳高度小于边坡开挖高度，边坡发生了失稳破坏。同时，通过分析可知，边坡在降水作用下可能会进一步降低其稳定性，所以在降雨条件下边坡失稳的可能性会大大增加，该计算结果与实际工程情况较为一致。

需要指出的是，公式(18)只适用于可视为大柔度杆件的研究对象，当研究对象为天然岩体时，需要满足μl/i>π(E/σp)1/2，此时计算出的边坡临界失稳高度较为合理。目前学者们提出的顺层岩质边坡失稳破坏模型较多，在实际运用过程中需要结合具体边坡实际变形破坏特征，在考虑边坡失稳机理的情况下选择合适的模型，否则得出的边坡临界失稳高度将失去意义。

4 结 论

本文首先对直立层状岩质边坡在自重荷载作用下的欧拉压杆失稳破坏模型进行了探讨，并将其建模思想推广到一般的顺层岩质边坡中；然后考虑到水力作用是诱发边坡失稳的一个关键因素，建立了考虑水力作用的顺层岩质边坡失稳破坏模型及其临界失稳高度的计算方法，同时考虑到岩石是一种自带损伤的地质材料，基于岩石微元强度服从正态分布提出了考虑水力作用与岩石损伤的顺层岩质边坡临界失稳高度的计算模型；最后结合顺层岩质边坡的实际工程案例，证明了该计算模型在实际工程案例中运用的可靠性和可行性。具体结论如下：

(1) 基于欧拉压杆理论提出的顺层岩质边坡失稳破坏模型比较符合边坡实际受力特征和破坏特征，计算得到的滑坡临界失稳高度与实际工程情况较为符合。通过对顺层岩质边坡失稳破坏模型的分析，发现边坡临界失稳高度受岩层倾角和内摩擦角的影响较大，总体呈现出随着岩层倾角增加边坡临界失稳高度减小、随着岩层内摩擦角增加边坡临界失稳高度增加的规律。

(2) 水力作用是诱发边坡失稳的重要因素，考虑水力作用的边坡失稳破坏模型计算出的边坡临界失稳高度值小于不考虑水力作用的边坡临界失稳高度值，说明地下水对边坡稳定性的影响是一个不可忽视的因素，考虑地下水作用的顺层岩质边坡失稳模型更能真实地反映边坡失稳破坏机制。将岩体视为损伤材料的顺层岩质边坡失稳破坏模型是在上述模型基础上的改进，该模型考虑岩体内部损伤，可以通过室内试验反映岩体在不同应力阶段的损伤变量，进一步反映不同阶段边坡临界失稳高度的变化，使得出的结论更加符合工程实际。

(3) 结合具体工程案例，运用考虑水力作用和岩石损伤的顺层岩质边坡失稳破坏模型定量计算出的边坡临界失稳高度与实际边坡失稳破坏高度基本一致，说明该模型在工程运用中具有一定的可行性。