考虑软弱夹层中岩土体应变软化特性的矿山边坡变形体渐进破坏分析

何 怡，郭 力，马 冲

(1.洛阳理工学院土木工程学院，河南 洛阳 471023；2.中国地质大学(武汉)数学与物理学院，湖北 武汉 430074)

随着我国经济建设的快速发展，对各类矿产资源的开采和利用效率提出了更高的要求，矿产资源开采逐步向高处、深部发展，以期满足不断增长的国民生产需求[1-3]。与深部矿山开采相比，露天采矿具有机械化程度高、高效率和低成本等优势，逐渐成为矿山开采的首选。但是露天采矿也会产生一些问题，其中较为典型的技术难题是：伴随开采过程的不断进行，矿山边坡不断增高，凹采深度加大，导致各种软弱地层暴露于自然环境中，由于降雨和地下水水位变化的影响，矿山边坡的稳定性受到严重威胁[4-8]。现有研究表明，岩体的失稳大多发生于软弱夹层处，此处的岩土体通常具有强度低、灵敏度高、应变软化等特点，对边坡的稳定性有着至关重要的影响[9-12]。

目前对于矿山边坡稳定性分析常采用极限平衡法，该方法在分析计算过程中并未考虑软弱夹层的应变软化特性，而这一特性对于高边坡变形体的稳定性有着非常重要的影响[13-15]。综合考虑软弱夹层中岩土体的应变软化特性，可以更合理、准确地评价矿山边坡的稳定性，对于滑坡预警和地质灾害评估也具有重要的指导意义。鉴于此，本文以四川某石灰石矿区高边坡平台变形体稳定性分析为研究对象，考虑软弱夹层中岩土体的应变软化特性对矿山边坡变形体稳定性的影响，基于线性应变软化M-S模型提出了容重增加法分析矿山边坡变形体渐进破坏的方法，并与极限平衡法进行对比，验证本文所提出的容重增加法计算边坡安全系数的可行性与优越性。

1 工程概况

四川某石灰石矿区采场滑坡区处于A平台，地势上总体呈南东高北西低，边坡横向宽400 m、纵向长300～400 m，微地貌类型为平台—陡坎—平台—陡坎—平台组合形式，最大海拔高差为390 m。台阶边坡高约10 m，平台宽约5～10 m，滑体厚10～58 m，体积约为380×104m3，根据边坡岩层的产状，判断为一大型顺层岩质边坡。

图1 某矿山边坡A平台变形体蠕变滑动Fig.1 Creep sliding of deformed rock body on platform A of a mine slope

图2 某矿山边坡软弱带泥化夹层Fig.2 Intercalated clay layer in weakness zone in a mine slope

根据现场勘察结果，该矿山边坡目前处于蠕动变形阶段(见图1)，边坡后缘出现了明显的张裂缝，左右两侧的变形尚不明显。结合区域地形地貌、地层特点、岩性组合和目前矿山的开采情况，初步推测该边坡变形的边界为：右侧边界为矿山开采后的切向边坡；左侧边界为原生山脊；剪出口为A平台临空面。该矿山边坡A平台变形体地层岩性主要由二叠系下统茅口组(P1m)中-厚层石灰岩组成，上覆碎石土等松散堆积物，下伏基岩为二叠系下统栖霞组(P1q)石灰岩(含软弱带泥化夹层)。该矿山边坡滑带土为软弱带泥化夹层(灰黑色，砂质泥灰岩含炭泥质，简称软弱夹层)，遇水后易软化，风化后常表现为碎片状，见图2。本矿区石灰石岩体构造裂隙和垂直形态岩溶发育，降雨入渗岩体后，向坡下顺层渗流，造成软弱夹层岩土体的强度降低，为矿山滑坡创造了条件。因此，软弱夹层的含水量是评价矿山的边坡变形体稳定性的重要因素。

2 考虑软弱夹层中岩土体应变软化特性的矿山边坡变形体稳定性数值计算模型建立

2.1 数值计算模型的建立

依据现场勘察和监测数据资料可知，对该矿山边坡A平台变形体稳定性有重要影响的关键因素是软弱夹层的含水量。因此，本文考虑软弱夹层中岩土体应变软化特性对矿山边坡变形体稳定性的影响，选取两个典型剖面并建立有限元数值计算模型，计算该矿山边坡变形体潜在滑动面在不同软弱夹层含水量条件下的稳定性，分析软弱夹层含水量对矿山边坡变形体渐进破坏的影响规律。

首先根据该矿山边坡A平台变形体潜在主滑面方向，选取1-1和2-2剖面作为典型工程地质剖面(见图3)，采用ANSYS软件进行前期处理，建立了两个剖面的数值计算模型(见图4)；然后将计算剖面分别划分为3个计算单元(岩性不同)进行了网格剖分，由于软弱夹层是重点研究区域，因此对其进行网络加密；最后将计算模型导入商业软件FLAC3D中进行数值计算，模型约束设置如下：左右边界和底部采用法向约束条件；上表面为自由面。

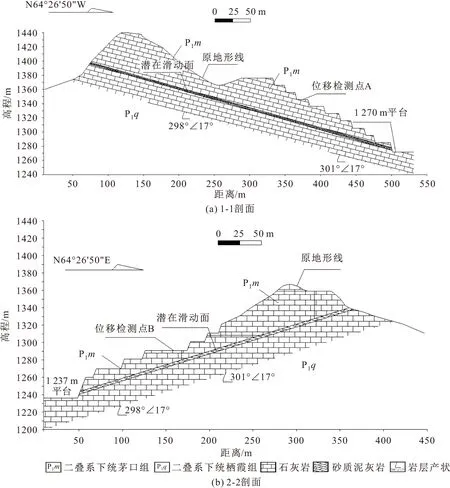
图3 某矿山边坡典型剖面工程地质剖面图Fig.3 Engineering geological profile of two typical profiles in a mine slope

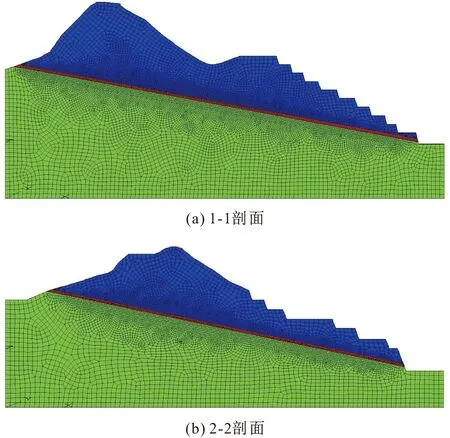
图4 某矿山边坡两个典型剖面的数值计算模型Fig.4 Numerical calculation models of two typical profiles in a mine slope

2. 2 应变软化与渐进破坏理论

根据前期的环剪试验结果[3,16]得知，该矿山边坡软弱夹层中岩土体具有明显的应变软化特征，即特定法向应力作用下，岩土体的抗剪强度在达到峰值后随应变增加呈不断减小的趋势，最终岩土体的抗剪强度趋于稳定。由此可以推断，该矿山边坡变形体的稳定性随时间和外荷载的改变而不同。本文选用线性应变软化摩尔-库仑模型(M-C模型)作为考虑岩土体应变软化的理论模型，模型假设岩土体软化阶段的强度参数与软化参数η呈线性关系。本数值计算模型中将塑性剪应变κps定义为应变软化参数，其增量形式的表达式为

(1)

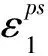
(2)

在数值计算模型中，考虑岩土体应变软化的Mohr-Coulomb强度准则的表达式为

=0

(3)

式中:σ1和σ3分别表示大、小主应力(MPa)。

常规数值计算大多在极限平衡或强度折减方法的基础上，计算滑坡体在不同阶段的安全系数，用以模拟边坡变形体的渐进破坏过程。对于应变软化材料而言，强度参数在不同阶段具有不同的特征，常规方法难以准确地描述边坡变形体的渐进破坏过程，故本数值计算模型利用容重增加法，通过有限差分手段，模拟考虑软弱夹层中岩土体应变软化特性的矿山边坡变形体的渐进破坏过程。该容重增加法以重力加速度为参考标尺，调整重力加速度至临界破坏状态，则边坡安全系数等于施加的重力加速度与标准重力加速度的比值。矿山边坡变形体渐进破坏过程与稳定性动态分析的步骤如下：①确定矿山边坡软弱夹层和变形体的基本强度参数，计算初始应力场；②设置最大计算时步为55 000步，每5 000步计算矿山边坡稳定状态；③调整重力加速度，计算不同时步、软弱夹层含水量条件下的矿山边坡安全系数。模型基本计算参数见表1。

表1 模型基本计算参数

3 数值计算结果分析与讨论

利用上述建立的考虑软弱夹层中岩土体应变软化特性的矿山边坡变形体稳定性数值计算模型，可计算得到不同软弱夹层含水量条件下所选的两个典型剖面矿山边坡安全系数随计算时步的变化，见图5。

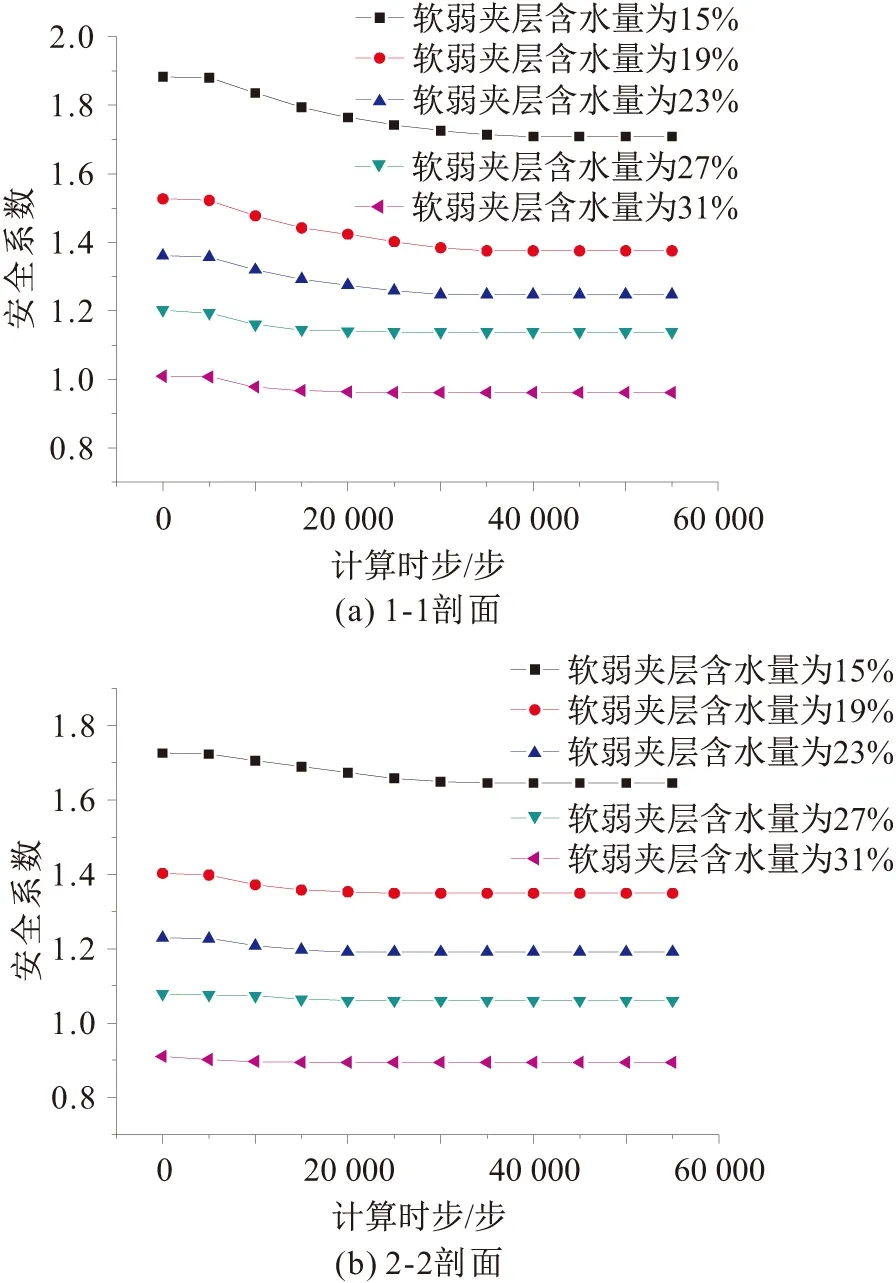
图5 不同软弱夹层含水量条件下两个典型剖面矿山 边坡安全系数随计算时步的变化曲线Fig.5 Variation of safety factor of the two typical profiles of a mine slope with calculation steps under different water contents of weak interlayer

由图5可以看出：

(1) 软弱夹层含水量越高，该矿山边坡的安全系数越低，这与前述得到的软弱夹层含水量增加会导致其抗剪强度降低，增加边坡滑动失稳风险的分析结果是完全一致的。

(2) 该矿山边坡安全系数随计算时步的增加而逐渐降低，最终趋于稳定；但对于软弱夹层含水量较高的情况(31%、27%、23%)，该矿山边坡从初始的安全系数到最终稳定的安全系数所需的计算时步较少；对于软弱夹层含水量较低的情况(19%、15%)，该矿山边坡初始的安全系数与最终稳定的安全系数的差值较小，对于边坡安全系数达到稳定的安全系数所需的计算时步也相对较多。

(3) 相同软弱夹层含水量条件下，1-1剖面的边坡安全系数高于2-2剖面的边坡安全系数，不同剖面位置处该矿山边坡安全系数的差异主要是由于软弱夹层产状及其与基岩的位置不同所造成的。

为了验证容重增加法用于分析矿山边坡变形体渐进破坏过程的优势，本文将常规极限平衡法计算得到的该矿山边坡安全系数与本文容重增加法的计算结果进行对比，具体见表2。

由表2可知，极限平衡法峰值状态下的矿山边坡安全系数Sp与容重增加法初始状态下的矿山边坡安全系数Si非常接近，这是因为软弱夹层岩土体的应变软化是从峰值状态开始的；两种计算方法对矿山边坡安全系数的影响甚微，不论是极限平衡法还是容重增加法，随着软弱夹层含水量的增加，矿山边坡安全系数的差值Δ逐渐减小，这表示高软弱夹层含水量条件下，软弱夹层中岩土体峰值状态的力学参数与最终状态的力学参数差别不大，软弱夹层中岩土体应变软化特征不明显；容重增加法下稳定状态的矿山边坡安全系数Sf略大于极限平衡法下残余状态的矿山边坡安全系数Sr，且两者的差值随着软弱夹层含水量的增加逐渐减小。众所周知，实际边坡滑动面的形成具有渐进性特征，即便滑面贯通之后，组成滑带的岩土体也未达到残余强度。因此，极限平衡法利用残余强度得到的矿山边坡安全系数Sr较为保守。本文基于应变软化M-C模型的容重增加法综合考虑了矿山边坡变形体的渐进性破坏过程，获得的计算结果与工程实际更为接近。

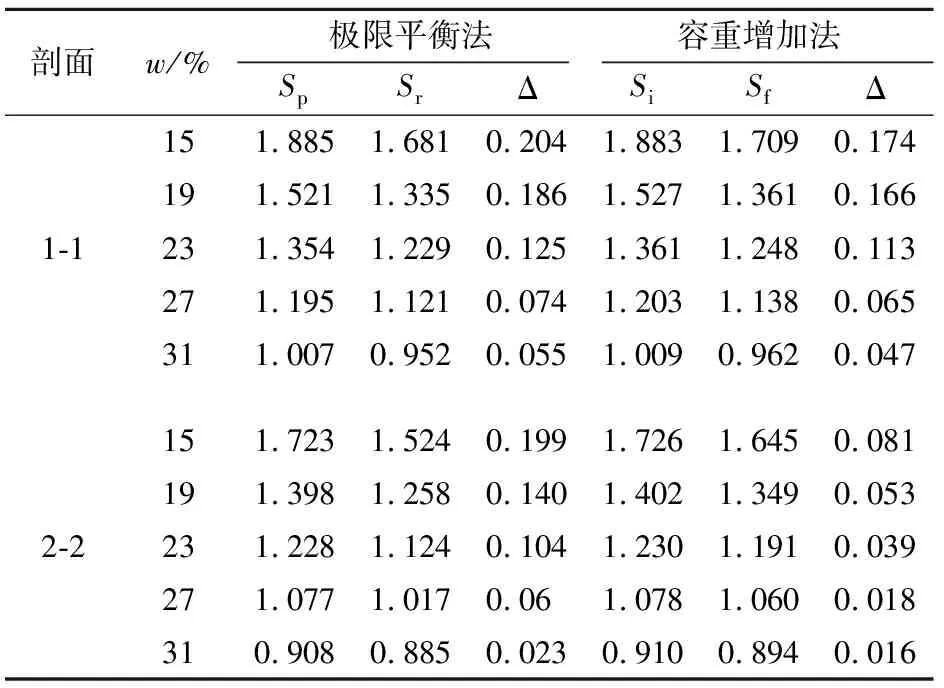
表2 某矿山边坡安全系数两种计算方法的结果对比

注：表中w表示软弱夹层含水量(%)；S表示矿山边坡安全系数；Δ表示矿山边坡安全系数的差值；下标p、r、i和f分别表示峰值状态、残余状态、初始状态和稳定状态。

为了直观地表示容重增加法在描述边坡变形体渐进性破坏过程的优势，本文以1-1剖面为例，计算得到软弱夹层含水量为23%的条件下剪应变增量随计算时步的分布云图,见图6。

由图6可见，随着计算时步的增加，边坡剪应变增量经历了从初始发生到最终贯穿整个滑动面的过程；当计算时步为5 000步时，边坡剪应变增量最先出现于坡顶处，当计算时步增加至15 000步后，边坡剪应变增量由坡顶处向下扩展，扩展途径与潜在滑动面一致；当计算时步增加至20 000步时，边坡剪应变增量扩展至坡脚处，贯穿整个滑动面；此后，增加计算时步并不会影响边坡剪应变增量的发生区域，由此表明该矿山边坡变形体的变形破坏达到一个稳定阶段，相应的矿山边坡安全系数值对应于表2中所述的稳定状态的安全系数Sf。

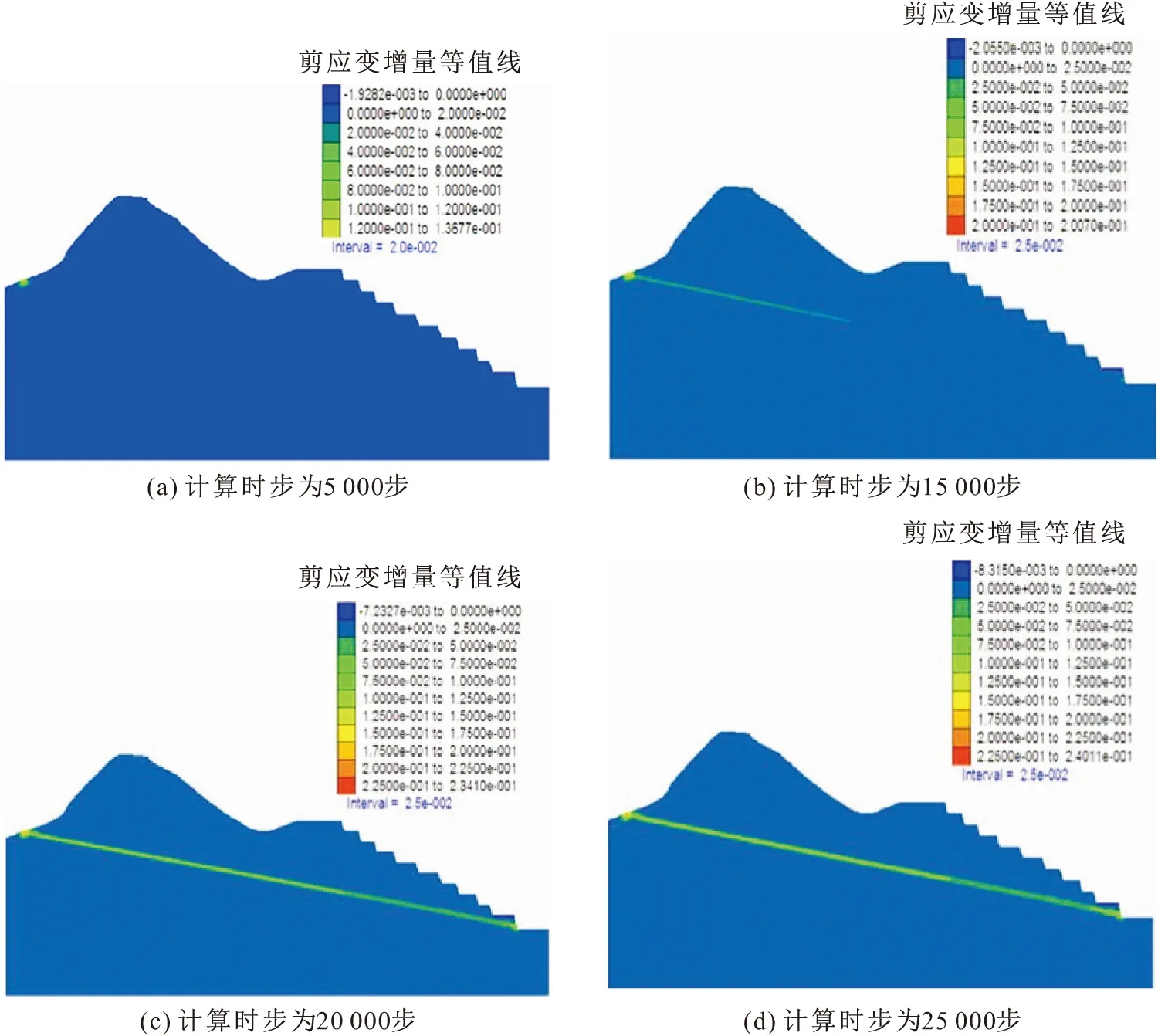
图6 某矿山边坡1-1剖面剪应变增量随计算时步的分布云图(w=23%)Fig.6 Variation of increment of shear strain of 1-1 profile of a mine slope with calculation steps with water content of 23%

4 结 论

(1) 软弱夹层的工程特性对于矿山边坡变形体的稳定性有着控制作用，其力学性能对含水量的变化较为敏感，因此在评价矿山安全风险时，应综合考虑软弱夹层中岩土体应变软化特性对矿山边坡稳定性的影响。

(2) 软弱夹层含水量的增大会增加矿山边坡失稳的风险，软弱夹层中岩土体的应变软化特性对矿山边坡变形体稳定性的影响亦逐渐增强。容重增加法初始状态下的矿山边坡安全系数与极限平衡法峰值状态下的矿山边坡安全系数相当，采用残余强度计算得到的矿山边坡稳定性结果偏于保守，而容重增加法稳定状态下矿山边坡安全系数的计算结果与实际更为接近。

(3) 基于应变软化M-C模型的容重增加法可形象地描述矿山边坡变形体的渐进破坏过程，明确边坡变形的发生部位、发展过程和最终稳定状态，这对于矿山边坡的失稳预警和稳定分析均具有重要的指导意义。