含共面双裂隙复合岩样力学特征的颗粒流分析

2020-05-21陈彦安崔德山李一冉梁文迪

安全与环境工程 2020年2期

陈彦安，崔德山，卞康，李一冉，梁文迪

(1.中国地质大学(武汉)工程学院，湖北武汉 430074；2.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉 430071)

地下洞室围岩往往由多种岩性特征相差悬殊的岩层组成，由于各层岩石基质的组成成分不同，复合岩层的力学特性和破坏形式与均质岩石相比具有很大的差异[1-2]，对隧道工程施工技术和工艺的选择具有较大的影响，因此复合层状岩体的各向异性已成为岩体力学和地下空间工程领域关注的焦点问题。如Hudson于2005年提出了假设，认为地下洞室的破坏是在洞周切向应力和临空层理面的相互影响下发生的；Tien等[3]、Cheng等[4]和程建龙等[5]通过两种相似材料交替复合配制成不同岩层倾角的复合岩样，并通过试验得到了岩层倾角对复合岩样强度参数和破坏模式的影响规律；郭志华等[6]对层状复合岩体进行了三轴压缩的有限元数值模拟分析，研究了软层倾角对层状复合岩体宏观力学特性的影响。

与均质岩层类似，复合岩层内也存在着大量的微裂纹、裂隙和节理等结构面，这些结构面的萌生、扩展和贯通会降低原岩强度，甚至造成工程岩体的失稳破坏，影响施工进度和安全。因此，研究含裂隙复合岩样的力学行为和破坏机制有着重要的工程应用价值。目前，对于裂纹拓展方面的相关研究大多是基于均一岩层开展的试验研究和数值模拟分析[7-13]。如殷鹏飞等[14]基于RFPA2D软件对含单裂隙复合岩层强度与裂纹扩展特征进行了数值分析。但目前鲜有对存在裂隙条件下复合岩层变形破坏特征的相关文献报道。

近年来，基于离散元法的颗粒流程序PFC[15](Particle Flow Code)在模拟岩石破裂、断续节理裂纹扩展[16-19]、边坡大变形[20-21]等方面表现出显著的优势，逐渐成为国内外岩土工程领域研究的有力工具。然而，这些研究大多是基于球形颗粒为计算单元开展的，无法很好地表征岩石中不规则矿物颗粒的结构特征。与传统颗粒模型不同，平面节理接触模型[15](Flat-Joint Contact Model)描述了颗粒表面之间刚性连接的理想化界面行为，可促使颗粒表现为不规则多边形，从而再现岩石矿物颗粒的晶体结构特征，克服了上述传统颗粒模型的不足[22-24]。鉴于此，本文基于前人的研究[4]，采用颗粒流软件PFC2D中的离散裂隙网络[15](discrete fracture network)、平面节理接触模型和平滑节理接触模型[25-26](smooth-joint contact model)等方法，通过预制不同倾角的共面裂隙，从数值模拟的角度分析了单轴压缩下裂隙倾角和岩层倾角对复合岩样强度与裂纹扩展特征的影响。

1 数值模型的建立

1. 1 建模步骤

在PFC2D软件中建立复合岩样的数值模型一般有如下几个步骤：

(1) 建立初始模型。数值模型尺寸与室内试样尺寸[4]相同，高100 mm、宽50 mm。在颗粒粒径取值上，本文借鉴岩石颗粒离散元研究成果[27-31]的取值经验，先将颗粒粒径比确定为1.33，使模型的非均质性趋近于现实岩样状态；再分别设置最小颗粒粒径分别为0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm，使颗粒在高100 mm、宽50 mm的空间中填充，不同粒径对应的颗粒总数统计见表1。由于当颗粒粒径过小时，模型颗粒的数量太多，会导致计算效率低下；而颗粒粒径过大则会导致颗粒总数太少，颗粒结构在应力作用下稳定性变差，计算结果的波动也较大[32]。因此，本文在数值模拟过程中综合考虑计算规模和颗粒粒径的敏感性，选取0.3 mm为颗粒的最小粒径。

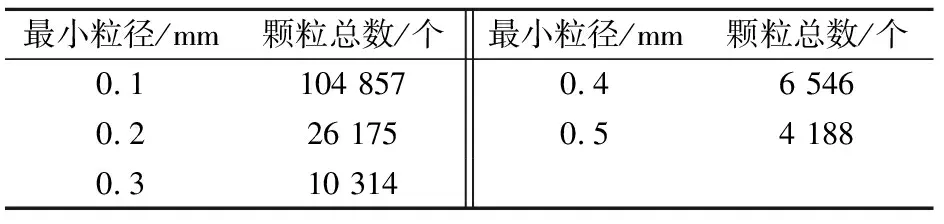
表1 不同粒径对应的颗粒总数统计

(2) 调整内应力。通过编写FISH语言实现对“墙”的控制，并不断调整模型边界位置，使颗粒体系间内应力均匀且处于低水平状态，删除黏结数少于3的悬浮颗粒。

(3) 设置颗粒黏结参数。为了更好地表征复合岩样的各向异性，本文采用软-硬混合平面节理材料来模拟岩石内部细观颗粒之间的接触，并引入离散裂隙网络表示软-硬岩层面，同时将与离散裂隙网络交叉的平面节理接触模型全部替换为平滑节理接触模型(见图1)，最后采用表2中的黏结参数对颗粒接触参数分别进行设置。

1. 2 软-硬两种材料参数的确定

采用表2中的黏结参数对颗粒接触参数进行设置，分别建立了软岩基质和硬岩基质的标准岩样模型，并通过编写FISH函数，实现对“墙”的控制，使侧“墙”处于极低的围压水平，再通过控制上、下“墙”的移动速度来对试样进行单轴加载，直至试样破坏。

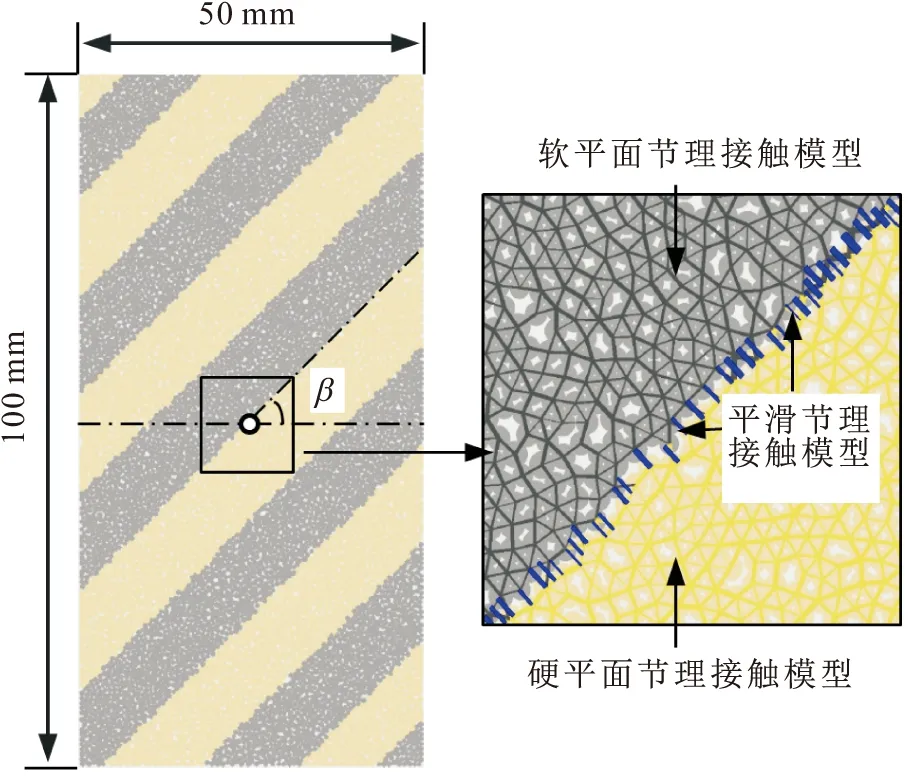
图1 完整岩样数值模型示意图Fig.1 Schematic diagram of numerical intact sample注：β为岩层倾角。

对于试样加载速率的选取，Zhang等[33]研究认为准静态加载速率上限为0.08 m/s。本文给定上、下两端“墙”恒定速度为0.05 m/s[13]，通过墙体的移动来对试样进行加载，符合准静态加载速率，与室内试验相吻合。

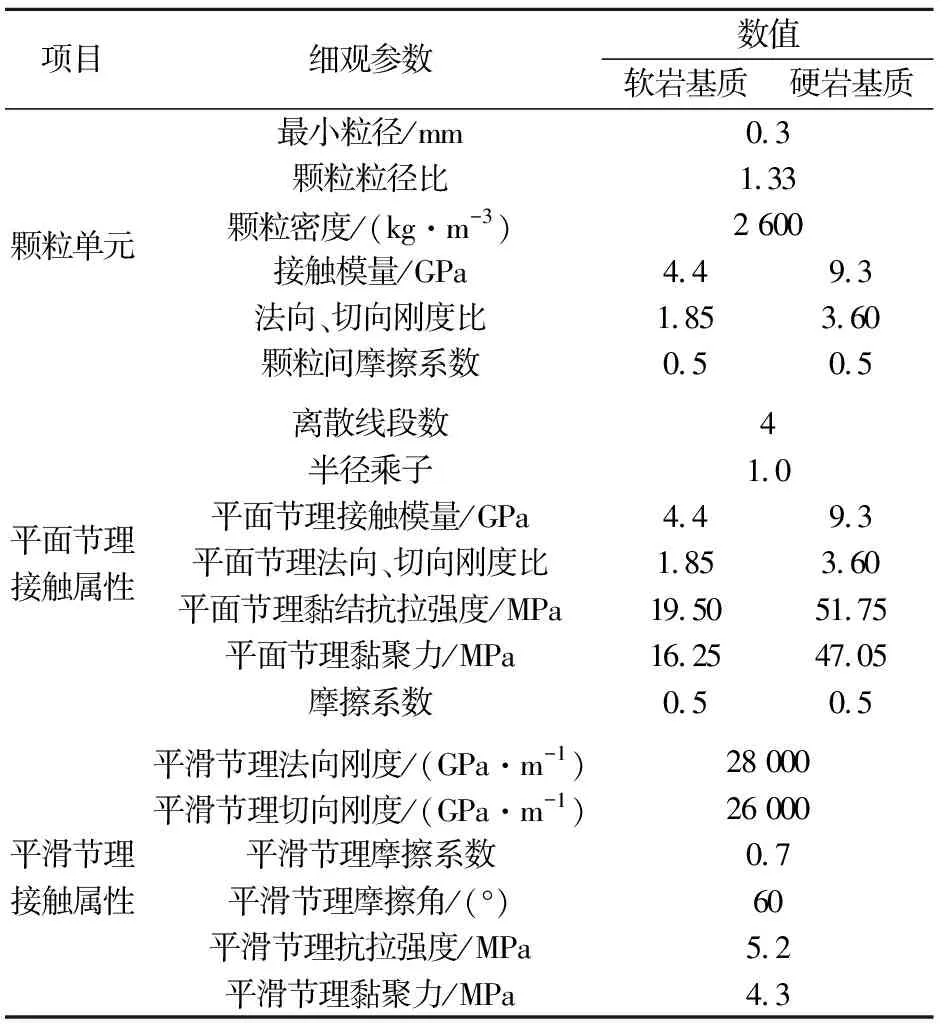
表2 PFC颗粒模型的细观参数

本文将模拟结果与Cheng等[4]通过室内单轴压缩试验所获得的软-硬两种材料的物理力学参数进行了对比，见表3。

表3 软-硬两种材料的物理力学参数对比

由表3可知，模拟结果与室内试验结果[4]的误差均小于4%，初步验证了所用参数的正确性。

1. 3 无裂隙复合岩样数值模型的构建

无裂隙复合岩样数值模型的构建方法按照第1.1节，在设置颗粒黏结参数时，对平面节理接触模型进行分组，然后依据表2对软岩基质和硬岩基质的细观参数分别赋值，从而建立岩层倾角分别为0°、15°、30°、45°、60°、75°、90°的复合岩样数值模型。

在软层基质和硬层基质的交界面处引入离散裂隙网络DFN，由于平滑节理接触模型在模拟结构面特征方面具有一定的优势[25-26]，故本文将与DFN交叉的平面节理接触模型全部替换为平滑节理接触模型，并保持平面节理接触模型的细观参数不变，采用“试错法”[34-38]对平滑节理接触模型参数进行调整，同时按照表2对其属性进行设置。

由于颗粒的随机分布会对计算结果产生影响，为了确保数值模拟的代表性，本文在确定颗粒粒径取值的前提下，通过选取不同的随机数种子，以6个随机分布状态进行研究。表4给出了单轴压缩下不同岩层倾角复合岩样的峰值强度和弹性模量随机模型6次重复计算的模拟结果。由于颗粒分布状态不同，不可避免地会存在宏观特性的离散化，因此本文选取6次重复计算模拟结果的均值与试验结果[4]进行了对比分析。

由表4可知，复合岩样的峰值强度和弹性模量的模拟结果与室内试验结果[4]相比其偏差很小。

图2和图3给出了单轴压缩下不同岩层倾角复合岩样的峰值强度和弹性模量PFC2D数值模拟结果与室内试验结果[4]的对比曲线。

由图2和图3可见，模拟得到的复合岩样峰值强度随岩层倾角的变化呈现出“N”型的变化趋势，与室内试验结果[4]基本吻合；而模拟得到的复合岩样弹性模量虽然随岩层倾角的变化不明显，但与室内试验结果[4]的差别很小，说明了所建模型的合理性。

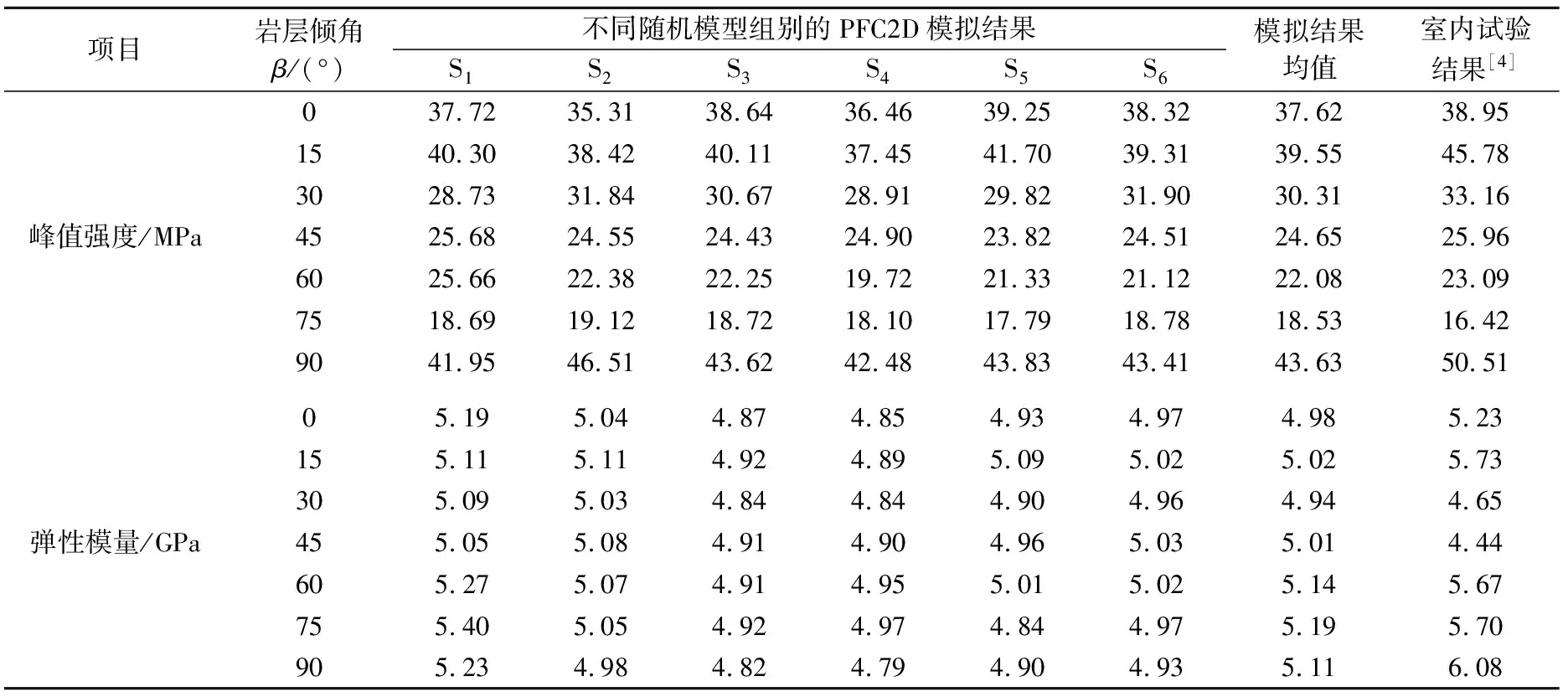
表4 单轴压缩下不同岩层倾角复合岩样的峰值强度和弹性模量的PFC2D模拟结果与室内试验结果[4]的对比

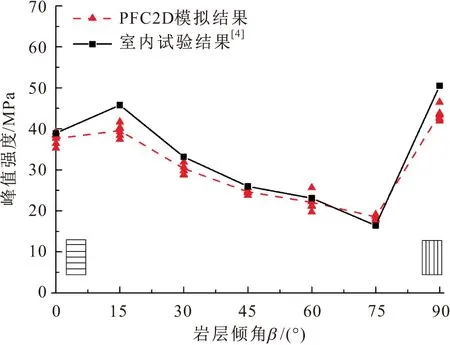
图2 单轴压缩下不同岩层倾角复合岩样的峰值强度 PFC2D模拟结果与室内试验结果[4]的对比曲线Fig.2 Comparison of the peak strength of the composite rock samples with different dip angles of strata under uniaxial compressive test between PFC2D numerical results and laboratory test results[4]

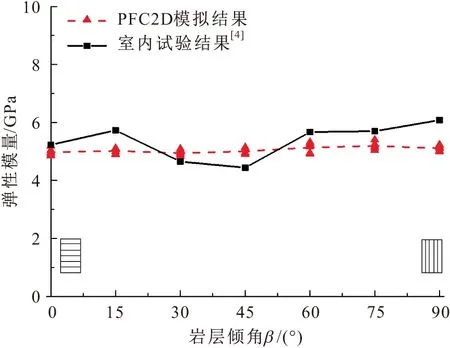
图3 单轴压缩下不同岩层倾角复合岩样的弹性模量 PFC2D模拟结果与室内试验结果[4]的对比曲线Fig.3 Comparison of the elastic modulus of the composite rock samples with different dip angles of strata under uniaxial compressive test between PFC2D numerical results and laboratory test results[4]

图4给出了单轴压缩下不同岩层倾角(0°～90°)复合岩样的应力-应变关系曲线PFC2D数值模拟结果(实线)与室内试验结果[4](虚线)的对比。

由图4可以看出：

(1) 复合岩样的应力-应变关系数值模拟曲线与室内试验曲线总体趋势相近，但存在一定的差异：复合岩样的应力-应变关系室内试验曲线在加载前期存在孔隙压密段，且弹性段曲线斜率随岩层倾角的变化有所差异，而复合岩样的应力-应变关系数值模拟曲线无孔隙压密段，且曲线斜率变化甚微。这是由于在PFC2D模拟中，颗粒已基本处于较为密实状态，从而在施压过程直接进入弹性阶段，且由于颗粒流模型内部孔隙不随黏结分组角度的变化而变化，因此其变形特征随岩层倾角的变化不明显；另一方面，室内试验所用的岩样虽由同一岩块钻取，但仍然不可避免地存在差异性。

(2) 数值模拟下不同岩层倾角复合岩样的应力-应变关系曲线有所不同，并呈现出一定的规律性：在相同的加载速率下，不同岩层倾角模型到达峰值应力时的应变不同，当岩层倾角为90°时复合岩样到达峰值应力时所对应的应变最大。加载前期，各复合岩样均表现出线弹性，当加载至一定程度时，各复合岩样变形特征开始产生分异，且随着岩层倾角的增加，复合岩样破坏形式逐渐由脆性(峰后应力骤降)向延性(峰后应力波动，并出现屈服平台)转化。关于复合岩样随岩层倾角变化的脆-延性转化机理，将在后面做详细分析。

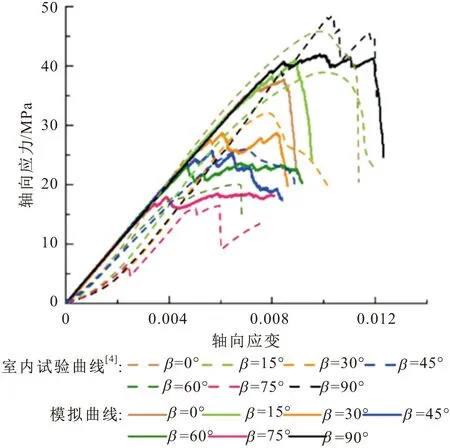
图4 单轴压缩下不同岩层倾角复合岩样的应力-应变关系曲线PFC2D模拟结果与室内试验结果[4]的对比Fig.4 Comparison of the stress-strain curves of the compo- site rock samples with different dip angles of strata under uniaxial compressive test between the PFC2D numerical results and laboratory test results[4]

表5为单轴压缩下不同岩层倾角复合岩样的最终破坏模式S1随机模型组别PFC2D模拟结果与室内试验结果[4]的对比。

由表5可以看出：

(1) PFC2D模拟与室内试验复合岩样的宏观破坏模式基本吻合，但略有不同：在室内试验复合岩样破坏图中，软层内裂纹集中程度较低，而在PFC2D模拟复合岩样破坏图中，大面积的细观破裂集中出现在软层内，而硬层中只有直线型的裂隙，这与数值模拟复合岩样内部软层、硬层、层面三种成分组合破坏的规律相关。由于层面间黏结强度较小，复合岩样内层间黏结首先发生破坏，此后靠层间摩擦力维持复合岩样整体性；随着加载的进行，由于软层黏结强度较低，软层内黏结先于硬层发生破坏，因而在软层内出现的微破裂较为集中；当软层内微破裂累积至一定程度时，加载应力才达到硬层内黏结的起裂应力，因此硬层中裂隙累积较少，呈现出直线型；当内部裂隙相互搭接、贯通时，复合岩样发生整体破坏。

表5 单轴压缩下不同岩层倾角复合岩样的最终破坏模式PFC2D模拟结果与室内试验结果[4]的对比

注：淡黄色表示硬层；深灰色表示软层。

(2) 不同岩层倾角复合岩样的宏观破坏模式体现出一定的规律，主要分为3种破坏模式：与层面交叉的张拉破坏、沿层理面发生的剪切滑移破坏和沿层理面发生的张拉劈裂破坏。与层面交叉的张拉破坏模式主要发生于低角度岩层倾角(β=0°～30°)复合岩样中；中等角度岩层倾角(β=45°～75°)复合岩样的破坏模式主要由结构面控制，主要发生沿层理面的滑移破坏，这也解释了为什么岩层倾角为75°时复合岩样的峰值强度甚至比软岩基质强度低的现象；高角度岩层倾角(β=90°)复合岩样的破坏模式主要为沿层理面发生张拉劈裂破坏。

综上所述，本文数值模拟结果与室内试验结果[4]尽管存在差异，但两者在复合岩样的强度特征、变形特征和宏观破坏模式方面随岩层倾角变化的规律基本一致。因此，可考虑将颗粒流模拟作为一种补充手段，来探究复合岩样内部的细观机制，这样可以消除材料自身的影响，结果更有利于岩层倾角的影响研究。同时，也证明通过PFC2D软件建立的复合岩样数值模型是合理、有效的，故可对该模型施加预制裂隙来做进一步的数值模拟分析。

2 含共面双裂隙复合岩样的破坏特征分析

2. 1 含预制共面双裂隙复合岩样数值模型的构建

文献[14]基于RFPA2D软件对含单裂隙复合岩层强度与裂纹扩展特征进行了数值分析，但其单裂隙设置部位主要位于软层基质之中，且并未考虑其对硬层基质的影响，也未对软层基质和硬层基质的交界面进行表征，因而该研究有一定的局限性。

基于此，本文采用删除颗粒的方法构建张开裂隙[13]，共面双裂隙几何尺寸见图5。保持裂隙长度和岩桥长度为10 mm，以试样形心为旋转中心对裂隙倾角α进行设置，裂隙设置部位跨越软岩基质和硬岩基质，克服了文献[14]的不足之处，使其研究成果具有一定的代表性。限于篇幅，本文主要以岩层倾角β为0°、30°、60°、90°的复合岩样展开研究，有针对性地将共面双裂隙倾角α分别设置为0°、30°、60°、90°、120°、150°，建立了含预制共面双裂隙复合岩样的数值模型，并通过对试样进行单轴压缩试验，分析了含共面双裂隙复合岩样的破坏特征。

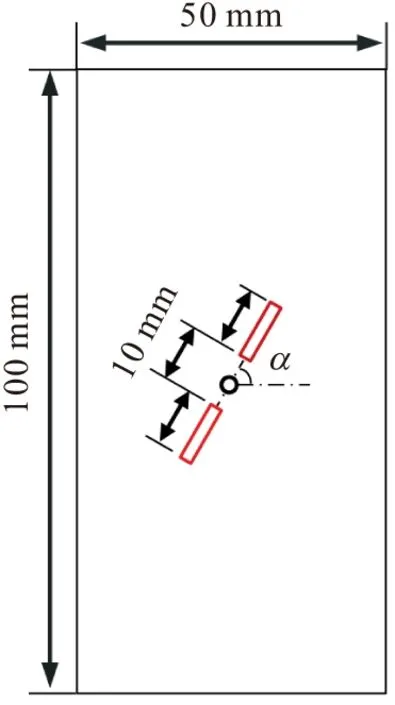
图5 共面双裂隙几何尺寸Fig.5 Numerical sample containing coplanar double fractures注：α为裂隙、岩桥倾角。

2. 2 含共面双裂隙复合岩样的力学特性参数分析

单轴压缩下，含共面双裂隙复合岩样的峰值强度和弹性模量，以及含共面双裂隙复合岩样的峰值强度与岩层倾角的关系曲线、弹性模量与岩层倾角的关系曲线的数值模拟结果，见表6、图6和图7。

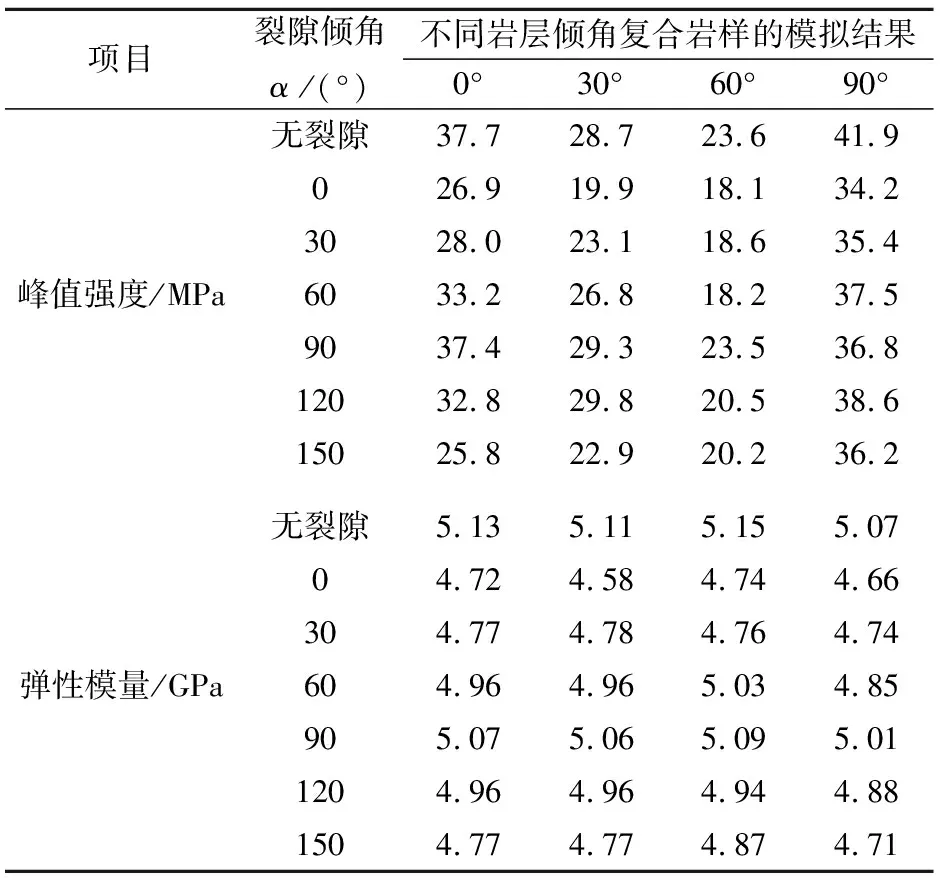
表6 单轴压缩下含共面双裂隙复合岩样的峰值强度和弹性模量数值模拟结果

由表6、图6和图7可以看出：

(1) 在低角度岩层倾角试样(β=0°、30°)、中角度岩层倾角试样(β=60°)和高角度岩层倾角试样(β=90°)中，含共面双裂隙复合岩样的峰值强度普遍小于不含裂隙复合岩样的峰值强度，体现了裂隙对复合岩样强度的削弱作用；当裂隙倾角α为90°时，含共面双裂隙复合岩样的峰值强度及其随岩层倾角的变化趋势与无裂隙复合岩样的基本相同，说明竖直裂隙对复合岩样强度的削弱程度最低；不同裂隙倾角下复合岩样的峰值强度随岩层倾角的变化呈现出相同的趋势，当岩层倾角β为0°～60°时，复合岩样的峰值强度先逐渐降低，至岩层倾角为60°时复合岩样的峰值强度达到最小值，然后再快速增加，至岩层倾角为90°时复合岩样的峰值强度达到最大值，文献[33]也得到了类似的结论，再次验证了本文数值模拟结果的合理性。

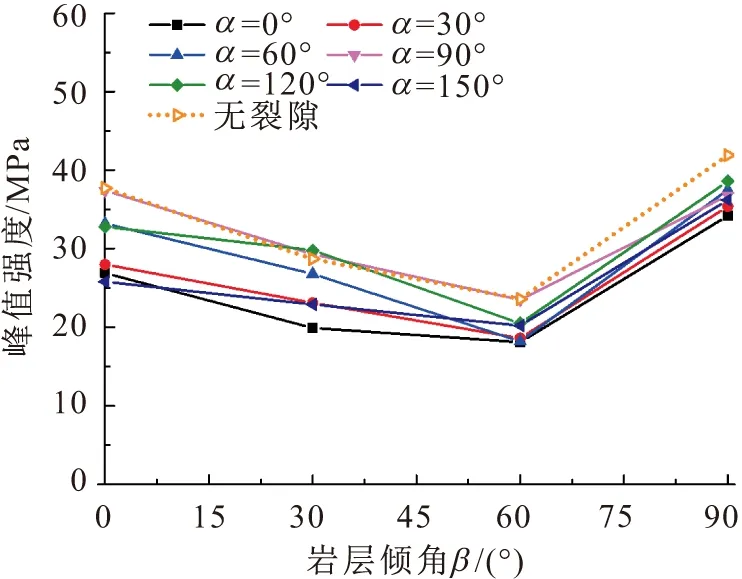
图6 单轴压缩下含共面双裂隙复合岩样峰值强度与岩层倾角β的关系曲线Fig.6 Plots of peak strength vs.dip angles β of the composite rock samples containing coplanar double fractures under uniaxial compression

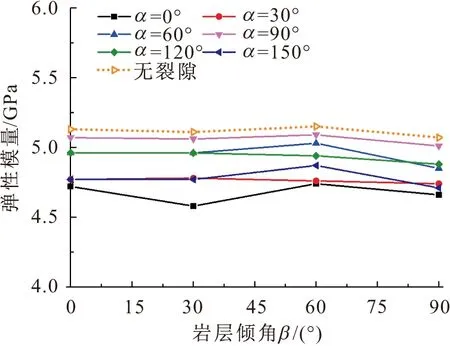
图7 单轴压缩下含共面裂隙复合岩样弹性模量与岩层倾角β的关系曲线Fig.7 Plots of elastic modulus vs.dip angles β of the composite rock samples containing coplanar double fractures under uniaxial compression

(2) 含共面双裂隙复合岩样的弹性模量普遍小于无裂隙复合岩样的弹性模量，体现了裂隙对含共面双裂隙复合岩样变形刚度的削减作用；同样，当裂隙倾角α为90°时裂隙对复合岩样弹性模量的削弱程度最低，说明竖直裂隙对原岩强度的折减效应并不明显；相同裂隙倾角下除个别含共面双裂隙复合岩样(0°、150°)的弹性模量随岩层倾角的变化产生波动外，总的来说其随岩层倾角变化并不明显。

2.3 含共面双裂隙复合岩样的应力-应变关系曲线和变形破坏特征分析

单轴压缩下含共面双裂隙复合岩样的应力-应变关系曲线，见图8。

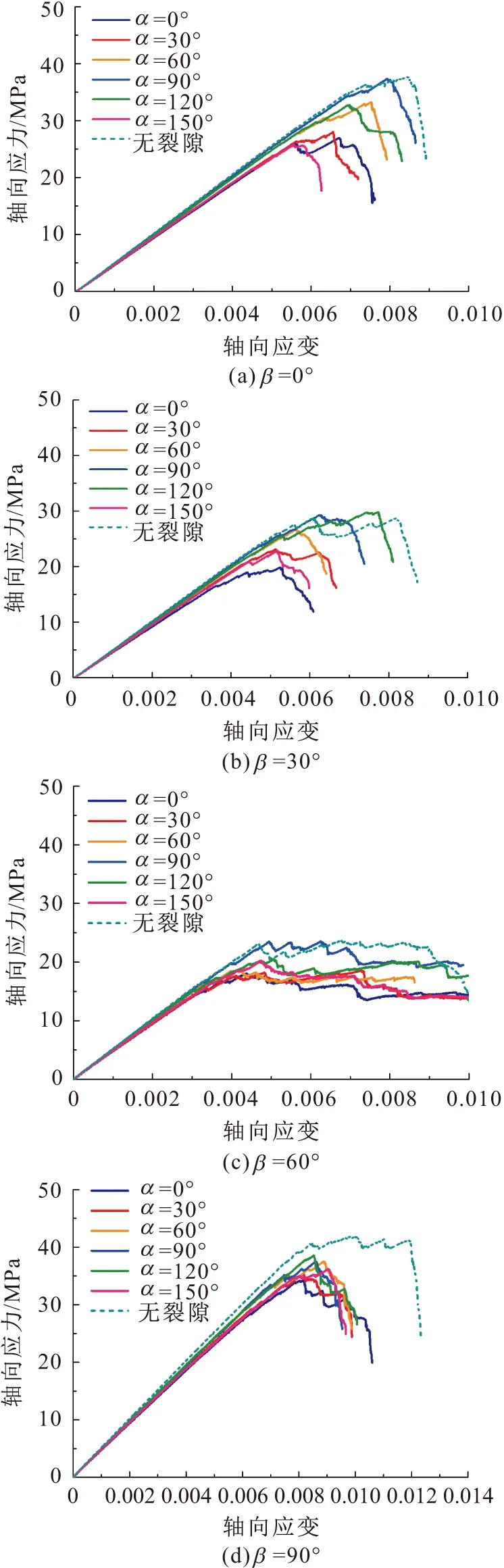
图8 单轴压缩下含共面双裂隙复合岩样的应力- 应变关系曲线Fig.8 Stress-strain curves of the composite rock samples containing coplanar double fractures under uniaxial compression

由图8可见，含共面双裂隙复合岩样的应力-应变关系曲线均可分为线弹性阶段、弹塑性阶段、峰后阶段3个过程，但在不同岩层倾角下含共面双裂隙复合岩样的变形破坏特征差异明显，具体表现如下：当在小角度岩层倾角下，含共面双裂隙复合岩样的变形方式主要以岩块(软层基质、硬层基质)的变形为主，因此表现为脆性破坏；从小角度到中角度岩层倾角(β=0°～60°)，随着岩层倾角的增加，含共面双裂隙复合岩样的变形逐渐转由结构面控制，以岩块沿层理面的滑移变形为主，其应力-应变关系曲线峰后形态由应力突降转为应力波动，并出现屈服平台，呈现出由脆性到延性破坏的趋势；从中角度到高角度岩层倾角(β=60°～90°)，由于含共面双裂隙复合岩样层面与加载方向的夹角不断减少，其整体变形方式由层面间的摩擦咬合转化为岩块内部变形，因此含共面双裂隙复合岩样的延性特征减弱，其强度和变形模量也得到了提高。