考虑螺栓连接的吊挂式薄壁柱壳固有特性分析

马 辉， 付 强， 李 坤， 樊富友

(1.东北大学 机械工程与自动化学院， 辽宁 沈阳 110819； 2.东北大学 航空动力装备振动及控制教育部重点实验室，辽宁 沈阳 110819；3.中国兵器集团公司 长沙机电产品研究开发中心， 湖南 长沙 410100)

螺栓连接薄壁柱壳结构应用较为广泛，如制导炸弹、导弹弹体均属于柱壳结构，并且各舱段之间多采用螺栓连接[1].螺栓连接结构导致整个系统具有不连续性，进而影响到系统的安全性、可靠性.此外，弹体在飞行过程中还可能因结构参数设计的不合理，在气流扰动下诱发共振，进而对弹体造成毁灭性破坏[2].因此，有必要对螺栓连接的薄壁柱壳结构进行动力学特性分析.

Liu等[3]基于界面接触理论，建立了螺栓连接薄壁筒结构的三维有限元模型.Tanlak等[4]基于梁-壳单元建立了简化的螺栓连接模型.Boeswald等[5]建立了螺栓连接薄壁壳结构的非线性有限元模型.文献[6-8]提出了无螺栓建模、混合建模及实体建模等多种建模方法，其中，基于接触的预应力法可考虑预应力对螺栓连接接触非线性的影响.Li等[9]研究了螺栓松动边界条件下对薄圆柱壳非线性模态特性的影响.

以上研究表明，现有关于螺栓薄壁柱壳结构的参数化建模，多采用周期对称的螺栓薄壁柱壳模型进行相关研究，较少考虑吊挂结构处螺栓连接的影响，而制导炸弹、导弹等多采用吊挂结构对其进行约束.因此，有必要对螺栓连接-吊挂式柱壳结构进行振动特性的研究.本文拟通过试验和仿真相结合的方式建立一种含螺栓连接的吊挂式薄壁柱壳结构，并分析自由/约束边界条件和法兰/吊挂处预紧力对结构约束边界条件下固有频率的影响.

1 数学模型及其验证

1.1 预应力模态

在螺栓连接中，接触压力分布的不均、接触面积的变化、接触面间摩擦力的存在等均会导致界面接触的非线性[10].接触问题实际上是通过求解满足系列接触约束边界条件下能量最小值的位移最优解，并通过位移最优解导出其他解[11].本部分仅涉及求解螺栓预紧力作用下系统的固有特性.预应力模态法求解系统固有特性分两个环节：静力学求解和模态求解.

系统的能量泛函表达式：

(1)

式中：Π(u)为系统总能量；Π1和Π2为系统动能和势能；Γe为接触边界；α为罚刚度；λN为拉格朗日乘子；gN为接触间隙.

含接触问题的静力学方程：

Mü+Keu-BcλN(α,u)=0.

(2)

式中：M为系统质量矩阵；Ke为系统结构刚度矩阵；u和ü为系统位移、加速度；Bc为接触约束矩阵.

考虑接触的静力学方程：

KU0-BcλN(α,u)=R.

(3)

式中R为预紧力.

根据静力学方程，求出初应力矩阵Kσ(u0),根据K=Ke+Kσ(u0),结合系统质量矩阵M,QZ模态求解算法，得出系统的固有频率和相应振型.

1.2 模型建立及对比

本文根据制导炸弹、导弹弹体结构(图1)，相关几何参数设置见图2.以简化的螺栓连接-吊挂式薄壁柱壳结构为研究对象，基于ANSYS软件建立了其有限元模型(图3).本文为了提高计算效率，分别采用梁-壳混合单元(Shell181-Beam188)和全实体单元(Solid185)进行有限元建模，并对比了相关计算单元数和效率(见表1).模型的材料参数：弹性模量E=195 GPa，泊松比υ=0.25，密度ρ=7 850 kg/m3.

在全实体模型中，螺母、螺栓头与法兰的接触通过接触单元Conta174和目标单元Targe170建立绑定接触对，而法兰之间的接触对则是采用相同的单元(Conta174-Targe170)建立标准接触且界面摩擦系数设置为0.2[12].在梁-壳混合模型中，整体建模采用壳单元，螺栓建模采用梁单元，法兰间的界面接触通过Conta174-Targe170单元构建标准接触，螺母-法兰/螺栓头-法兰作用区域采用梁的端节点与作用区域刚性绑定来进行模拟.

基于ANSYS软件中的预紧力单元Prets179实现螺栓预紧力的施加.预紧力的计算公式：

T=kFd.

(4)

式中:F和T分别为预紧力和拧紧力矩；k为拧紧力矩系数；d为螺栓公称直径.本文中，T=6 N·m，k=0.2[13]，d=6 mm.本文假定螺栓同时拧紧，进而对接触压力及其分布进行分析.

1.3 接触压力试验验证

选用FUJIFILM压力测量胶片对螺栓连接的接触压力分布进行测量.图4表明12个螺栓的压力分布几乎一致，因此，试验仅需测试其中1个螺栓的压力分布.此处选用低压(2.5～10 MPa)和高压(10～50 MPa)压力试纸分别进行测量.当接触压力超过压感试纸的最低感压值时，压力试纸将显示为图4中的灰色区域.

图4将试验结果与仿真结果进行了对比验证.从图中可以看出：梁-壳混合单元模型和实体单元两种模型的接触面上的接触压力分布趋势一致，即两法兰接触面间的接触压力呈圆形分布，且随着接触压力分布区域逐渐靠近圆心，压力值不断增大.

在图4a中，低压试纸染色半径r1≈6.5 mm，且高压试纸的染色半径r2明显小于低压试纸染色半径r1，验证了上述接触压力分布规律，而在图4b和图4c中大于10 MPa接触压力的接触半径r3≈r4≈7.5 mm，比试验测得的半径r1大，这是由于试验件的法兰接触面由于加工误差等原因，没有保证绝对平整，但这并不影响验证接触压力的分布规律.

表1列出了采用实体/混合模型对图4进行计算时所需的单元信息、节点信息和计算时间.从表中可以看出，梁-壳混合单元模型比实体单元模型具有更少的单元数以及更高的计算效率.基于此，混合模型将被用于后续部分的仿真分析(在约束模态分析中，实体模型的计算时间是9 min 14 s，混合单元模型的计算时间是1 min 58 s，可以看出计算效率有很大的提高).

2 系统固有特性分析

本节主要研究了自由/约束边界条件下，螺栓连接-吊挂式薄壁柱壳的模态特性，并通过试验进行了对比验证.在仿真与试验验证时，拧紧力矩均为6 N·m.

2.1 自由边界下系统固有特性

自由边界条件下的有限元模型如图3a所示.图5为搭建的自由模态测试台，试验所用加速度传感器为联能CA-YD-125压电式加速度传感器.试验中采用对角多次拧紧的方式对螺栓进行预紧，然后将试验件通过橡皮绳悬挂于刚性杆，从而模拟自由边界.

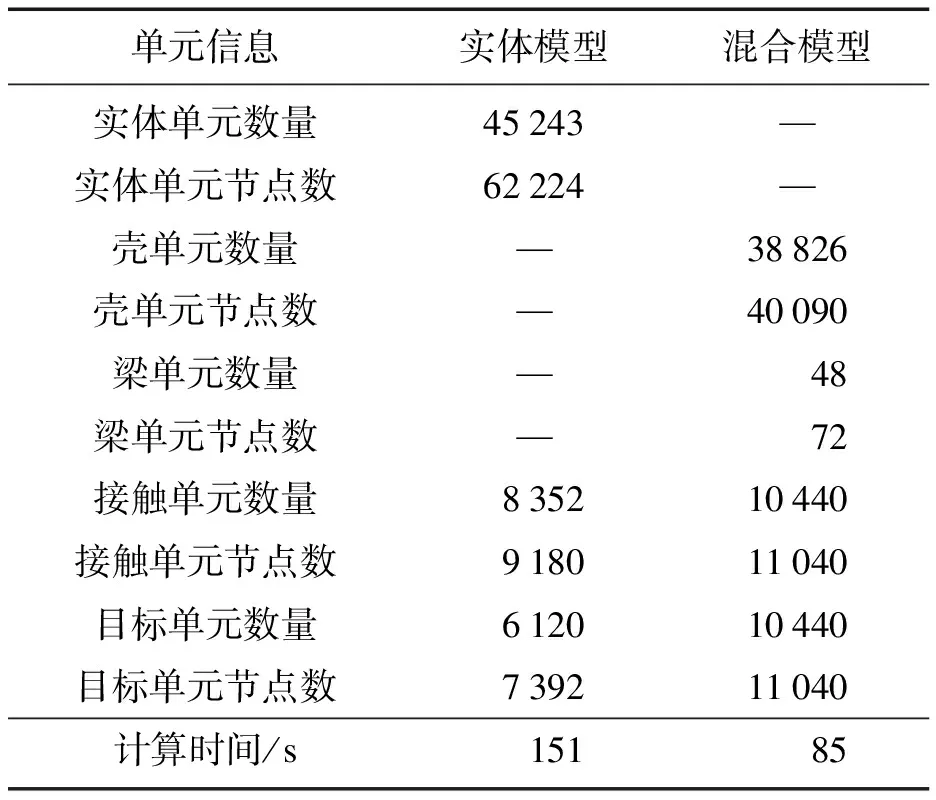
表1 不同建模方法单元数以及计算效率

为测得结构的振型图，在所测薄壁圆柱壳上布置96个测点，如图6所示.其中，沿圆周方向分布有16个测点，薄壁柱壳的轴向分布有6个测点.测试过程中，在图6的A点布置一个单向加速度传感器，采用多点输入单点输出的模态测试方法对薄壁圆柱壳进行固有特性的测试，振型图通过测试系统来进行绘制.

表2列出了试验和仿真得到的系统前8阶固有频率.从表中可以看出，试验和仿真所得固有频率吻合较好，从而验证了所建立模型的有效性.图7给出了系统前8阶振型图的仿真与试验结果.

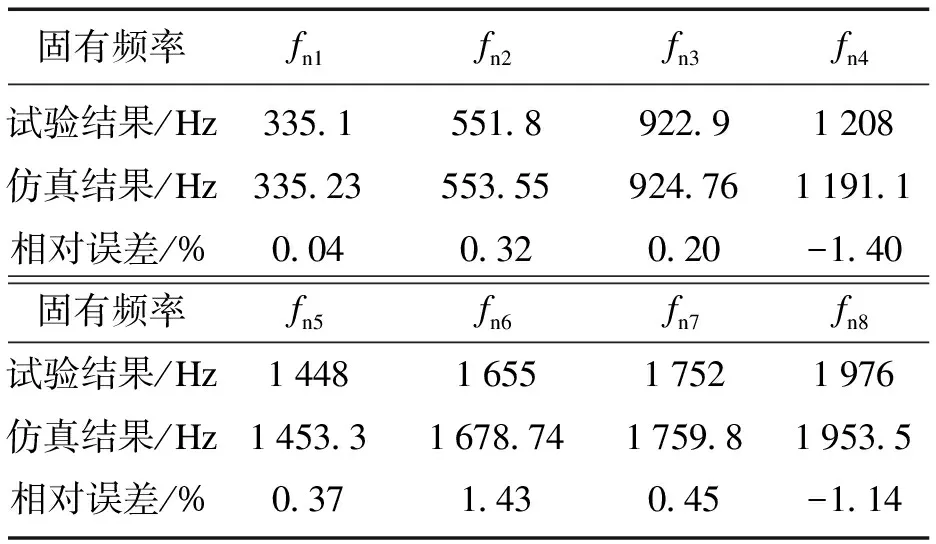
表2 自由边界条件下前8阶固有频率对比结果

2.2 约束边界下系统固有特性分析

考虑吊挂边界约束的影响，分别采用试验(图8)和仿真 (图3b)分析了系统的固有特性.基于所建立的有限元模型，进一步分析了法兰以及吊挂处螺栓预紧力对系统固有特性的影响.需要说明的是，法兰处用M6螺栓预紧，而吊挂处则采用M10螺栓预紧.

图9表明约束模态的振型不同于自由模态(图7)，其周向波数主要发生在高频，而低频主要表现为俯仰或周向波数较少的振型，且轴向波数较少.约束模态试验中的测点分布及测点数为沿圆周方向均匀布置8个测点，而沿轴向布置3个测点.

基于图8所示的试验测试结构与测点布置，对结构进行约束模态的试验测试.由于本文主要关心吊挂式薄壁柱壳结构的振动特性，因此，只考虑薄壁柱壳本身的振型结果，所测得结构的前8阶固有频率由表3列出.前8阶仿真振型图与试验结果对比，如图9所示，由图可知仿真和实测振型吻合良好.

2.2.1 法兰处螺栓预紧力的影响

图10为吊挂处螺栓连接预紧力不变的情况下，法兰处螺栓预紧力对系统固有频率的影响.从图中可以看出，随着螺栓预紧力的增大，系统的固有频率不断增大.这主要是由于螺栓预紧力的增大导致了螺栓连接处法兰的弹性变形增大，结合面贴合更加紧密，螺栓连接刚度增大.此外，法兰处螺栓预紧力对系统前4阶固有频率影响较小，因为前4阶振型主要表现为以吊挂为中心的摆动与俯仰振型.表4为图10的具体数值结果.

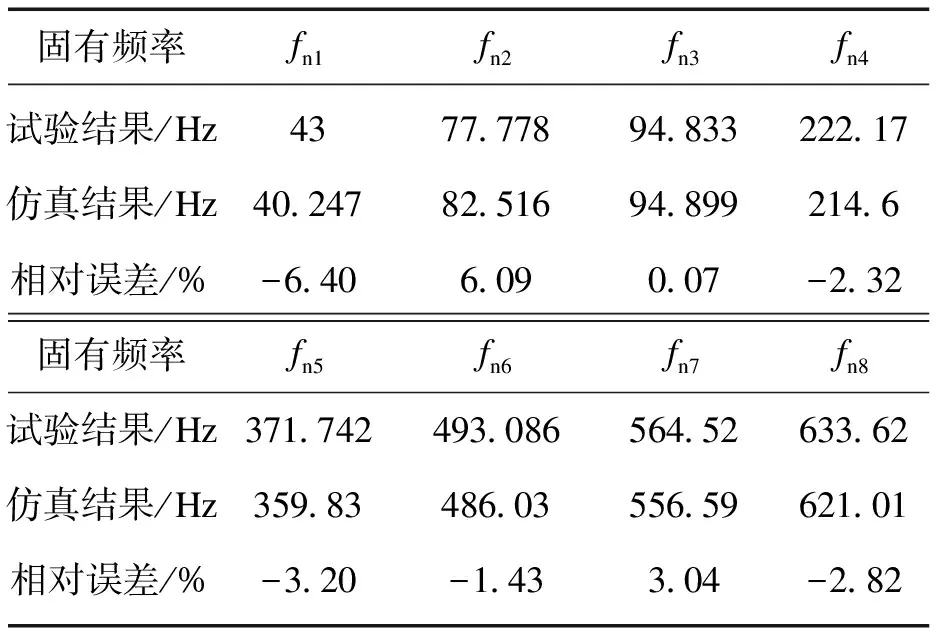
表3 吊装边界条件下前8阶固有频率对比结果

2.2.2 吊挂处螺栓预紧力的影响

图11为法兰处螺栓连接预紧力不变的情况下，吊挂处螺栓预紧力对系统固有频率的影响.从图中可知，随着预紧力的增大，系统固有频率不断提高，并且可以看出：相比于法兰连接处的螺栓预紧力，吊挂处的螺栓预紧力对系统前3阶固有频率影响较大，对第4～8阶固有频率影响较小，这主要是因为约束边界条件下系统的前3阶振型主要为俯仰型.为了从量的角度更清楚地了解影响程度，表5为固有频率随约束位置处预紧力变化的具体变化数值.

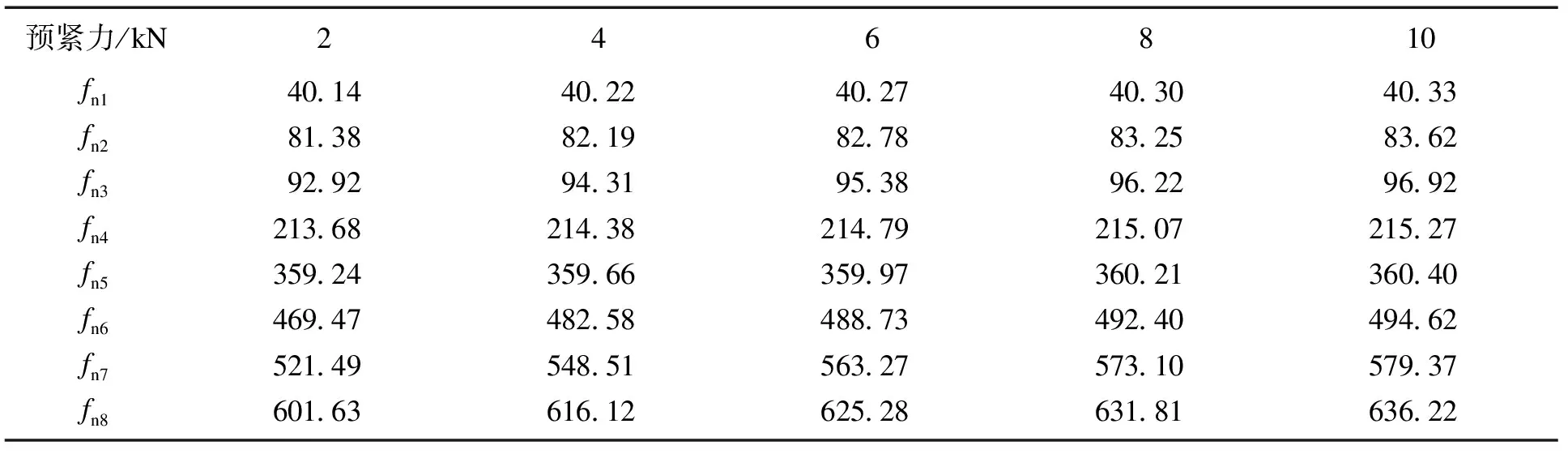
表4 法兰螺栓处不同预紧力下系统的固有频率值

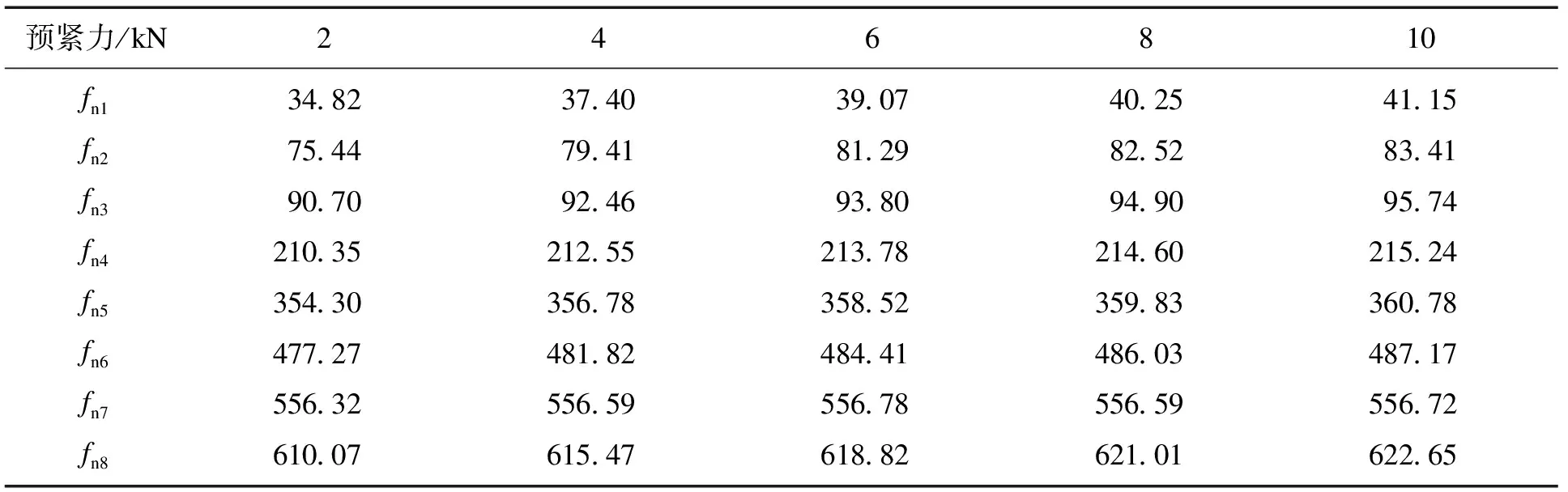
表5 约束位置处不同预紧力下系统的固有频率值

3 结 论

1) 在保证求解精度的条件下，本文建立的梁-壳混合单元建模比实体单元建模的求解效率更高.

2) 建立吊挂约束之后，薄壁柱壳-支架耦合系统的固有频率降低了很多，且薄壁柱壳结构低阶振型存在俯仰型，吊耳处螺栓连接对薄壁柱壳结构振动特性有很大影响.

3) 当吊挂处螺栓预紧力一定时，随着法兰连接处螺栓预紧力的增大，系统第5～8阶固有频率变化最明显且呈逐渐增大的趋势；当法兰连接处螺栓预紧力一定时，吊挂处螺栓预紧力对系统前3阶固有频率具有明显影响，且随预紧力的增大呈增大趋势.