浅谈如何用底层逻辑命题
2020-05-19查双剑
查双剑

【摘要】原创,不是在已建成的房子上重新装潢,而是要重新打地基、造新房。教育工作者需要深入理解知识的底层逻辑,从底层逻辑出发,根据所要考查的目标,去构建原形题,再以原型题作为基础,去搭建新问题。
【关键词】底层逻辑;原型;增加变量法;逆命题
2019年4月底,笔者承担了《2018—2019学年度贵池区三级教研网络中片第三次联考》数学科目的制卷工作。这里笔者以试卷的第23题为例,谈谈自己的命题心得。
一、关于底层逻辑
1.什么是底层逻辑
我们的认知符合“从特殊到一般”“从具体到抽象”的规律。其中的“一般”“抽象”就是通常所讲的原理、本质。比如,在宏观世界中,所有物体运动状态的改变都是由自身所受外力引起的,力就是原理、本质,力改变运动。逻辑推理中也存在这样的“力”,笔者称之为“底层逻辑”,它推动了逻辑的展开。举个例子,任意画一个三角形,通过拼接或测量,我们发现“三个内角和都等于180°”,所以我们可以大胆猜想:“所有的三角形内角和都等于180°(三角形内角和定理)。”这就是“从特殊到一般”的过程。在证明这个猜想时,它是通过构造平行线,将三个内角集中成共顶点的一个平角完成证明的。根据该定理,我们又可以进一步演绎推理出“三角形的外角等于和它不相邻的两个内角和”,我们称之为“推论”。其中,通过构造平行线转移角用到了“平行线性质定理”,而“平行线性质定理”又是根据公理——“同位角相等,两直线平行”得到的,逻辑逆向推理到这里就不能再继续了。整个过程的逻辑链条是,公理—定理1—定理2—推论。以上例子中,以公理为起点,引出的一系列逻辑推理就是笔者说的“底层逻辑”。
2.使用底层逻辑构建问题
原创,不是在已建成的房子上重新装潢,而是要重新打地基、造新房。教育工作者需要深入理解知识的底层逻辑,从底层逻辑出发,根据所要考查的目标,去构建原形题,再以原型题作为基础,去搭建新问题。
二、构建原型
1.底层逻辑
如图1,∠ABC=∠BDE=∠BFC,则△ABC ∽ △BDE。
2.特殊化
如图2,∠ABC = ∠BDE = ∠BFC,若AB = BD,
则△ABC ≌ △BDE。
3.再特殊化
把图2结构放置到正三角形中,并引入动点,形成动图。如图3,在正三角形ABC中,点D、E分别是边BC、AC上的动点,AD、BE相交于点F,若∠AFE=60°(这里隐含了∠AFE = ∠ABD = ∠BCA,AB = BC),則△ABD ≌ △BCE。并且,根据圆的相关知识可得,点F在以AB为弦的圆弧上。
4.类比衍生
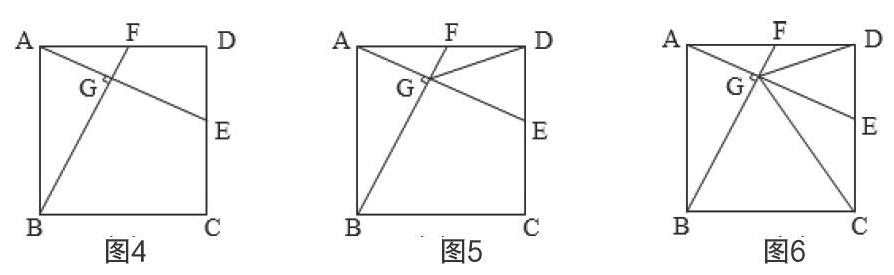
也可以把图2结构放置在正方形中。如图4,在正方形ABCD中,点E、F分别是边CD、AD上的动点,连接AE、BF,交于点G。若∠AGB=90°,则△ABF ≌ △ADE,并且点G在以AB为直径的半圆上。
我们还可以类比出正五边形、正六边形等例子。
三、命题过程
1. 原型题
这里笔者选择正方形作为“地基”。
如图4,在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G, 交AD于F。 (1)求证:AF=DE。
2.增加变量法
笔者采用“增加变量法”,提高问题难度。这里,有一个简单逻辑:当变量(连线)增加时,图形变复杂了,显然可供思考的点更多了,也就更难了。当点E移动时,点F、G也随之移动,点G的移动轨迹是以AB为直径的半圆,这是一个动态的过程。当连接GD时,增加了一条线段(GD)、两个角(∠FGD,∠DGE)。围绕这几个量,可以展开思考,提出问题。在提出问题时,考虑到考生的计算水平,选择该动态过程中某些“恰好”的时刻,更便于考生计算。比如,讨论GD的最值、∠FGD的大小等。这里,笔者通过角提出问题。
如图5,在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G, 交AD于F。 (2)连接DG,若DG平分∠EGF,求证:点E是CD中点。
在提出问题时,首先研究了这样一个动态的过程:随着点E移动时,点F的移动情况,发现当点E是CD中点(CE = DE)时,点F也是中点(AF = DF),当连接DG后,发现GD恰好平分了∠FGE,满足以上条件的点G显然只有一个。换言之,如果GD平分∠FGE,则点E也是CD中点。简单地说,分析时,是从边找角;提问时,是从角找边。
这里有一个命题心得,将原型题中发现的真命题的条件和结论互换,判断其逆命题是否依然成立,提出问题,往往会收到意想不到的效果。这里从角切入提问,是因为笔者在平时教学中发现,很多学生不善于找角并利用角的关系去解决问题。所以当从角切入提问时,就提高了问题的难度,使问题变得更具有开放性。
3.继续增加变量
在上述的条件下,连接CG,如图6,求证:CG=CD。
四、定稿
如图4,在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G, 交AD于F。
(1)求证:AF=DE;
(2)连接DG,若DG平分∠EGF,如图5,求证:点E是CD中点;
(3)在(2)的条件下,连接CG,如图6,求证:CG=CD。
【参考文献】
[1]罗国兴.初中数学教学中逻辑思维能力的培养分析[J].名师在线,2019(05):57-58.
