地基沉降作用下埋地聚乙烯管强度失效的数值模拟

罗 利， 马 燕， 张永军， 刘一江， 刘 秀,2

(1.湘潭大学 土木工程与力学学院， 湖南 湘潭 411105;2.湘潭大学 岩土力学与工程安全湖南省重点实验室， 湖南 湘潭 411105)

聚乙烯(PE)管具有耐腐蚀、长使用寿命、易施工等优点，在给排水和燃气输送领域已逐渐取代传统的金属管和水泥管，并得到普遍应用[1-2]．这些管道通常被埋置在地下，铺设成错综复杂的网络，联系着千家万户，成为关乎国计民生的重要生命线．但由于地下水过量抽取或地震等引起的地基不均匀沉降，影响了埋地管道的正常使用，导致其失效与破坏，从而危及人民的生命与财产安全．因此，对地基沉降作用下埋地管道失效与破坏问题的研究具有重要意义．目前，国内外已开展了部分与埋地管道相关的研究．如Takada等[3-4]用土箱沉降对埋地管道进行了一系列试验，发现地基沉降时，管线会发生弯曲变形，在一定沉降范围内，管线应力与沉降变形存在线性关系，试验的设置、过程和结果为后续研究提供了重要参考．高惠瑛等[5]针对地震引起的地层沉陷现象，将管道分为沉降区管道和非沉降区管道，研究表明沉降区管道变形随沉降量增大逐渐呈三次方幂函数曲线状态．陈志磊[6]针对地基沉降引起的地下管道破坏问题，模拟并分析了地基土沉降中管道的破坏特征及机理．余娟[7]分析了地下管道发生土体沉陷时的变形情况，根据沉陷区和非沉陷区交界处管道的形变，探讨了沉陷量对管道应力的影响．Luo等[8]对地基沉降作用下埋地管道的强度失效和力学性能进行了数值模拟．周敏等[9]通过下调控制模型箱底板的不同位移模式来模拟地层沉陷的形成和发展，研究了埋地高密度聚乙烯(HDPE)双壁波纹管道的受力变形特征，并进行了模型试验分析．Guo等[10-11]基于三硝基甲苯(TNT)当量法对埋地平行输气管道力学响应和安全间距进行数值研究与分析．尽管埋地PE管的失效与安全问题受到人们广泛关注与探讨，但仍然有待更多、更深入的研究．为此，本文对PE管在地基沉降作用下的变形与强度失效进行了模拟与分析，确定了沉降过程中危险区段的位置、管道服役的安全条件及其影响因素，以期对PE管的合理设计及安全评估提供一定的指导．

1 本构模型与恒速拉伸试验

PE材料是典型的黏弹性材料，具有明显的时间相关性和率相关性．Suleiman等[12]针对HDPE的本构模型进行研究，提出了双曲线本构模型：

(1)

式中：σ为应力；ε为应变；a、b为与应变率相关的材料参数．

图1 不同应变率下PE试样的拉伸试验数据与拟合曲线Fig.1 Experimental data and the fitted curves of PE specimens under various of strain rates

根据上述拟合结果，可获得不同应变率下参数a和b的值，其与应变率的关系曲线见图2．由图2可见，参数a、b与应变率的对数呈近似线性关系．为此，采用对数模型对参数a、b进行拟合，得到拟合方程(式(2)、(3))，再结合式(1)，得到PE管的率相关本构方程(式(4))：

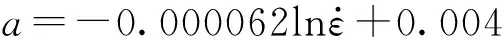
(2)

(3)

(4)

由于埋地PE管道受长期积累的地基沉降是一个缓慢渐变的过程，相当于准静态荷载作用，而准静态加载速率一般为1×10-6～1×10-5s-1[13]，故本文选用应变率1×10-5s-1作为模拟应变率.此应变率下PE本构关系如式(5)所示：

(5)

考虑到PE管的破坏形式以屈服失效为主，采用Mises屈服准则判别PE管的失效行为．根据Mises屈服准则，Mises等效应力σeq应不超过屈服应力σy，如式(6)所示：

(6)

式中：σ1、σ2、σ3分别为第一、第二、第三主应力．

根据试验结果，屈服应力与应变率的对数呈线性增长(见图3).由此，通过数值拟合，得到屈服应力与应变率的关系式，如式(7)所示：

(7)

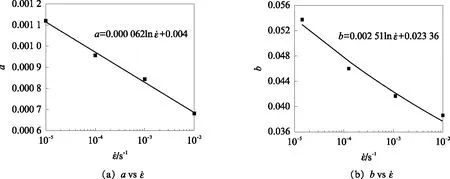
图2 参数a、b与应变率的关系曲线Fig.2 Relationship between a, b and strain rate

图3 PE管屈服应力随应变率的变化情况Fig.3 Variation of yield stress of PE with strain rate

综上所述，当应变率为1×10-5s-1时，PE管初始弹性模量E0为893MPa，屈服应力为15.8MPa.PE管材的材料参数如表1所示．

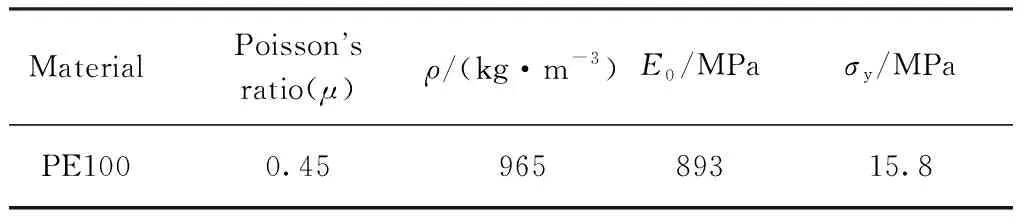
表1 PE管的材料参数

2 有限元模型

2.1 基本假设

(1)不考虑管道系统中的管件和连接件，PE管为非线性黏弹性且满足各向同性.

(2)管道相对于整体来说过薄，因此，使用壳体分析以简化计算.

(3)使用足够大的土体长宽来模拟无限大的土体，边界的设定主要基于圣维南原理，忽略远处土体的影响，大部分边界采用固定约束.

(4)管土间的相互作用为有限滑移接触．

2.2 材料参数

PE管的本构模型采用式(5)，材料参数见表1．土体模型采用扩展的Drucker-Prager(D-P)本构模型[15]，其具有以下特点：(1)考虑了围压的影响，并能反应土体的剪胀性；(2)可以模拟蠕变功能以描述材料的长期非弹性变形；(3)可以模拟单调加载下材料的力学行为．该模型在有限元软件中得到了广泛应用.土体Drucker-Prager模型的材料参数和硬化参数如表2、3所示．

表2 土体Drucker-Prager模型的材料参数

Note：c—Cohesion of soil mass;φ—Internal friction angle of soil mass;E—Deformation of soil mass;μ—Friction factor between pipe and soil;β—Internal friction angle;κ—Flow stress ratio;Ψ—Shear expansion angle of soil mass.

表3 土体Drucker-Prager模型的硬化参数

Note:σ1,σ3—X,Zprincipal stress;εp—Plastic strain.

2.3 模型尺寸

埋地PE管受到土压力和地面荷载的作用，各种外荷载最终均以土压力的形式作用于管道，对埋地管道的受力分析主要针对管土作用下的应力和变形．因此，在模拟过程中应考虑管周土体的影响.为了尽可能减少边界条件的影响，尽量取大模型地基长度和深度，有限元模型取为10m×3m×2m(长(L)×宽(W)×高(H)).考虑到管道几何形状和所受载荷的对称性，取1/2模型进行计算，模型尺寸及网格划分如图4所示.沿管道轴线方向分3部分：沉降段、过渡段和非沉降段，其中沉降段长度为 5m，过渡段长度分别为0、1.0、1.5、2.0m，非沉降段长度分别为5.0、4.0、3.5、3.0m；考虑埋地燃气管道在车行道下的最小要求值(GB 50028—2006《城镇燃气设计规范》)，管道埋深取为0.9m.PE100管公称直径为110mm，标准尺寸比为SDR11，公称壁厚为 10mm．

图4 地基沉降下管土体系有限元模型Fig.4 Finite element model of pipe soil system under foundation settlement

2.4 管土相互作用和边界条件

考虑到PE管的非线性大变形特性，选用Abaqus进行有限元建模与分析．有限元分析分3步进行，包括初始分析步、接触分析步和加载分析步．

(1)初始分析步 定义模型的初始边界条件，同时设置管道和土体的接触对，PE管与土之间有法向和切向2个作用方向，法向作用关系设置为“硬接触”来保证压力在接触面之间不会受到影响，切向作用关系摩擦系数设为0.18[16]．管土接触为面面接触，管道设置为目标面，土体设置为接触面，由于非沉降区域不受载荷的影响，X、Y、Z方向设置为固定约束，其余表面均施加X与Z方向的位移约束，中间平面施加对称性约束，管道的约束施加和土体相同，见图5(其中UX、UY和UZ分别表示X、Y和Z方向的位移).此步施加的边界条件运用到整个分析步中．

图5 有限元模型的载荷和边界条件Fig.5 Load and boundary conditions of the finite element model

(2)接触分析步 对整个模型区域施加重力荷载9.8N/kg，PE管内壁施加工作压强0.4MPa．

(3)加载分析步 沉降表现为整个沉降区域下降一定的位移，对沉降区上表面施加向下的位移约束 0.5m，在此位移作用下计算得到PE管的位移变形，如图6所示．PE管轴向沉降位移分布情况如 图7 所示．

图6 PE管随沉降位移的变化情况Fig.6 Variation of PE pipe with settlement displacement

图7 PE管轴向沉降位移分布情况Fig.7 Settlement displacement of PE pipe in the axial direction

3 结果分析与讨论

3.1 PE管的应力分布和屈服分析

本文主要探讨PE管垂直于沉降段的情况，水平方向无位移，管道两侧的应力水平较低，PE管屈服失效发生在管底或管顶位置．当沉降位移为 0.5m 时，PE管的Mises应力云图如图8所示．由 图8 可知：PE管的最大Mises应力约为33.3MPa，已超过管材的屈服应力15.8MPa，这意味着PE管已经达到屈服状态，局部已失效，无法继续安全使用；最大 Mises 应力位于过渡段与非沉降区交界处的管道顶部以及过渡段与沉降区交界处的管道底部．PE管的最大Mises应力随沉降位移的变化情况如图9所示，由图9可见：刚开始沉降时，由于沉降位移相对较小，由弯曲和内部压力引起的应力值均较小，在弯曲和内压的共同作用下，PE管的危险截面发生在过渡段与沉降区交界处的管道底部；随着沉降位移的增加，管道的弯曲程度越来越大，由此引起的应力也越来越大，管道的危险截面转移至过渡段与非沉降区交界处，PE管应力的大小由这2个区域的弯曲程度决定．

图8 沉降位移为0.5m时的Mises应力分布Fig.8 Mises stress distribution at a settlement displacement of 0.5m

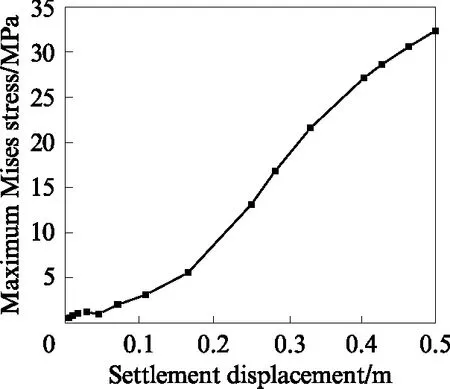
图9 最大Mises应力与沉降位移的关系Fig.9 relationship between the maximum Mises stress and the settlement displacement

图10为PE管上下表面轴向Mises应力分布情况．由图10可见，在沉降过程中，Mises应力在过渡段与非沉降段交界处、过渡段与沉降段的交界处这2个区域迅速增加.这是因为由沉降位移引起的弯曲应力占据了相当大的比例．

图10 PE管上下表面的轴向Mises应力分布情况Fig.10 Mises stress in the axial direction of the upper and lower surfaces of PE pipe

3.2 过渡段长度对管道屈服的影响

在地基沉降过程中，过渡段长度是影响PE管应力分析的一个重要因素．因此，在沉降位移为0.5m的情况下，进一步分析过渡段长度为0、1.0、1.5、2.0m时PE管的应力情况．图11显示了不同过渡段长度下，PE管最大Mises应力随沉降位移的变化情况，由图11可见：PE管的最大Mises应力随沉降位移的增加而增大；在沉降位移不变的条件下，PE管最大Mises应力随过渡段长度的增加逐渐降低，这主要由于过渡段长度越大，曲率的变化率越平缓，弯曲应力的变化率随之降低；在过渡段长度分别为0、1.0、1.5、2.0m时，PE管受沉降作用可安全使用的最大沉降位移是0.16、0.28、0.44、0.68m.图12为不同过渡段长度条件下使PE管屈服的沉降位移.由图12可知，随着过渡段长度的增大，沉降位移错位逐渐增大，使PE管达到屈服失效的沉降位移增大，且屈服失效的沉降位移与过渡段长度存在一种近似的指数关系．这是由于过渡段长度的增大，使得在同等沉降位移水平下，过渡段与沉降区交界处以及过渡段与非沉降区交界处的弯曲变形及曲率减小；而沉降位移对交界处弯曲曲率变化率的影响随着过渡段长度的增大而减小，进而PE管在该交界处发生屈服所需的沉降位移随之增大．在相同沉降位移条件下，短过渡段管道先屈服，因为在较小的区域发生较大的位移错位，管道的弯曲程度较厉害．

图11 不同过渡段长度条件下PE管最大Mises应力随沉降 位移的变化Fig.11 Variation of maximum Mises stress with settlement displacement under PE pipe with different length of transition section

图12 不同过渡段长度条件下使PE管屈服的沉降位移Fig.12 Settlement displacement of PE pipe at yield with different length of transition

4 结论

(1)PE管的最大Mises应力随着沉降位移的增大而增大，危险段发生在过渡段与沉降区或非沉降区的交界处．

(2)在过渡段长度分别为0、1.0、1.5、2.0m时，PE管受沉降作用可安全使用的最大沉降位移是0.16、0.28、0.44、0.68m．

(3)过渡段为位移交错区，随着过渡段长度的增加，致使PE管屈服的沉降位移逐渐增大，即在相同的沉降位移下，过渡段长的埋地PE管道较过渡段短的要安全些．