泡沫混凝土动态力学性能及本构关系
2020-05-19黄海健宫能平穆朝民
黄海健, 宫能平, 穆朝民, 周 辉, 刘 伟
(安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室, 安徽 淮南 232001)
作为轻质混凝土的代表,泡沫混凝土材料以其性能优异、造价低廉及环境友好等特点,从众多的节能环保型材料中脱颖而出.目前针对泡沫混凝土材料的力学相关研究多集中于材料改性及静态力学性能.陈兵等[1]研究了纤维增强泡沫混凝土的相关性能.Nambiar等[2]研究表明:孔体积、孔径、孔间距均影响泡沫混凝土强度和密度,孔径分布越均匀,强度越高;气孔形状对其性能没有影响.Falliano等[3]研究表明:水胶比对泡沫混凝土抗压强度影响极大;不同性质的发泡剂导致制品微结构中的空隙排列不同;与在玻璃纸片内固化相比,在空气中固化的制品抗压强度最低.Kearsley等[4]研究发现,泡沫混凝土的抗压强度随着密度的减小呈指数函数形式减小.在动态力学性能研究方面,袁璞等[5]解决了泡沫混凝土类低阻抗多孔介质材料透射信号采集难的问题,采用灵敏系数较高的半导体应变片可较好地捕捉微弱的透射信号,实现对泡沫混凝土类多孔介质材料近似恒应变率的动态压缩试验.王建国等[6]研究了分层介质对冲击的响应,发现泡沫混凝土在应力波的冲击作用下,气孔发生坍塌破坏,不仅产生了大的变形,而且吸收了大量的能量,在宏观上表现为泡沫混凝土强度较低,但具有较大的极限变形.
由于泡沫混凝土越来越多地应用于防震、抗冲击设计中,因此有必要对其动态力学性能进行进一步的研究.本文以分离式霍普金森压杆(SHPB)装置为试验平台,研究了泡沫混凝土的动态力学性能,借鉴宏观损伤变量及朱-王-唐模型,通过改进、拟合建立了反映泡沫混凝土峰值应力前动态应力-应变关系的近似等效本构方程.
1 试验设计
1.1 混凝土试件的制备
按照表1中的配合比将水泥、粉煤灰、水、聚丙烯(PP)纤维和外加剂混合均匀,并倒入添加量为 1.2m3/m3的泡沫,搅拌成均匀流浆态,倒入模具后养护制成泡沫混凝土(FC).普通混凝土(OC)采用标准C50混凝土制备而成.经静态力学试验得到试件物理力学性能指标,见表2.

表1 泡沫混凝土配合比

表2 物理力学性能指标
1.2 试验装置及原理
1.2.1试验装置
1.2.2试验数据处理
SHPB试验通常采用三波法进行数据处理,由于试验采集的入射信号与反射信号十分接近,在计算入射端应力时,常由于测试数据误差导致计算结果偏差很大.针对泡沫混凝土材料的特殊性,采用简化的三波法进行数据处理,见式(1).
(1)
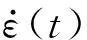
2 泡沫混凝土冲击试验结果及分析
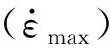

图1 泡沫混凝土应变率时程曲线Fig.1 Time-strain rate curves of foam concretes
图2为不同最大应变率下泡沫混凝土的动态应力-应变(σ-ε)曲线,因曲线波动较大,为清晰起见,只选取其中4个展示.由图2可见:不同最大应变率下泡沫混凝土的动态应力-应变曲线形态基本相似,均具有较长的弹性上升阶段和较短的塑性变形阶段;随着最大应变率的增大,动态弹性模量增加,峰值应力逐渐变大,试样达到峰值应力后进入应变软化阶段.

图2 不同最大应变率下泡沫混凝土的动态应力-应变曲线Fig.2 Dynamic stress-strain curves of foam concrete at different maximum strain rates
在加载初期,泡沫混凝土试件孔壁骨架具有一定的承载能力,此阶段荷载由孔壁骨架来承受,动态应力-应变基本呈线性关系,符合胡克定律,部分入射应力波能量转化为试件的弹性变形能.但由于其内部孔洞形成了诸多自由面,导致信号采集效果不佳,噪波影响较大,造成线弹性阶段动态应力-应变曲线的较大波动.
为了排除试验系统大范围误差造成的较大数据波动,同时与泡沫混凝土形成对比,设计了1组普通混凝土的SHPB试验,其动态应力-应变曲线如图3所示.由图3可见:普通混凝土的动态应力-应变曲线初始阶段呈上凹型,为混凝土原有裂隙和孔隙受压后逐渐闭合所致;闭合阶段过后,曲线近似为线性;随着加载的继续,裂隙扩展,局部破坏加大,到达屈服极限,曲线斜率下降,试件切线模量逐渐降低,随后快速进入应变软化阶段.排除试验系统的大范围误差后,与普通混凝土应力-应变曲线相比,泡沫混凝土的应力-应变曲线存在2个显著特征:第一,整段曲线上下波动较大,在破坏阶段尤为明显;第二,在应变软化阶段,应力值并没有快速下降至完全丧失承载力,而是形成了1个较高的应力平台,并且最大应变率越高,应力平台表现得越长、越显著.
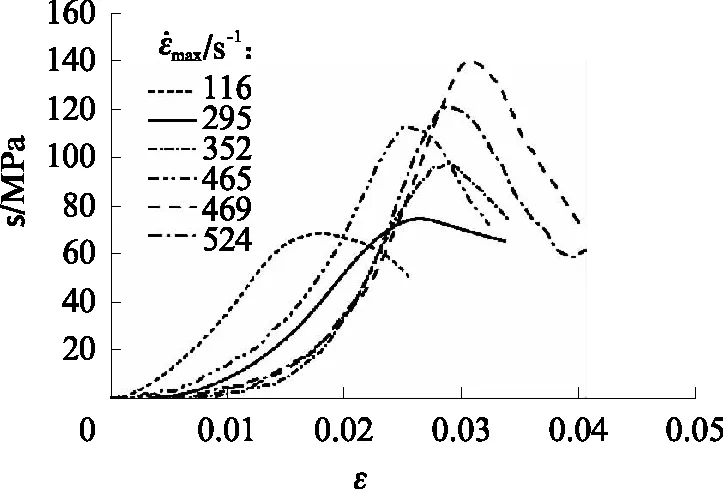
图3 普通混凝土试件的动态应力-应变曲线Fig.3 Dynamic stress-strain curves of ordinary concrete specimens
泡沫混凝土为多孔材料,诸多研究表明,多孔结构对材料力学性能的影响极大[7].在受到冲击加载时,由于其内部孔洞分布不均匀,较弱的孔洞产生破坏时,该孔洞周围产生应力集中,导致破坏在此孔洞周边沿垂直于应力的方向向四周扩展,直至该层混凝土被均匀压实后应力释放;随着加载的继续,压实层的上、下侧孔洞相互接触,重复进行上述破坏过程直至试件整体被压实、破坏.当首先破坏的孔洞层被压实破坏时,该层应力卸载,应力随应变增加而减小;在压实层两侧孔洞接触并被压实的过程中,应力则随应变增加而小幅度增加.图2中,上述破坏过程表现为应力-应变曲线破坏阶段形成较明显的上下波动的应力平台;由于较高最大应变率下泡沫混凝土的破坏形式更倾向于逐层塌落破坏,因此最大应变率越大,动态应 力- 应变曲线中的平台越明显.
那是,那是,老田赶紧附和。听说,这片地以前是乱坟场,种啥都壮。老田突然想起昨晚老婆给他出的主意,正好由着这无花果说开来。这鬼把戏,也就是吓吓胆小的女人,男人哪畏这个?
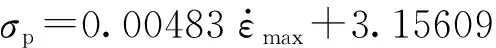
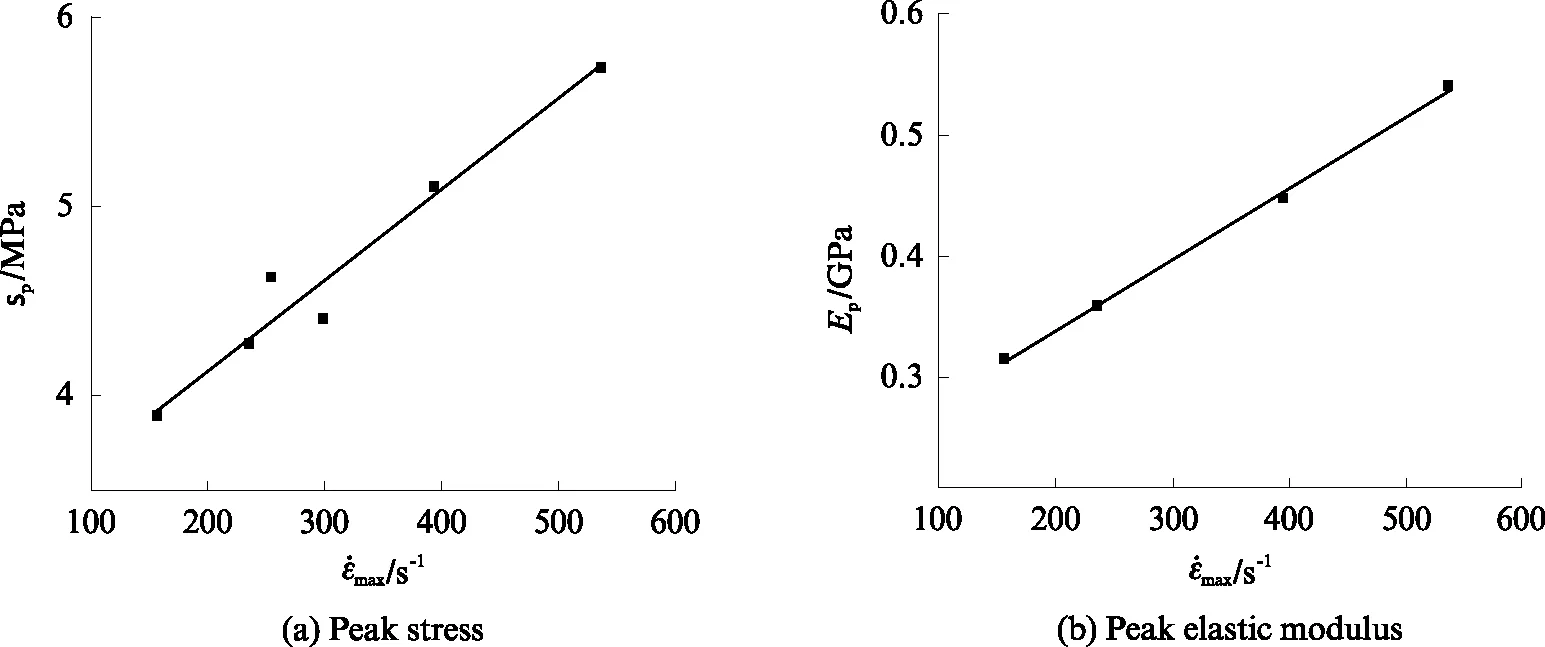

图4 变形参数随最大应变率的变化趋势
为对比冲击载荷和静态载荷作用下混凝土的强度,引入动态增长因子(DIF):
(2)
式中:fc,d为混凝土动态抗压强度,fc,s为混凝土静态抗压强度.
动态抗压强度可由混凝土应力-应变曲线获得,静态抗压强度取值为表2中的峰值应力.泡沫混凝土和普通混凝土动态增长因子随最大应变率变化趋势如图5所示.由图5可知,2种混凝土的动态增长因子均随最大应变率增加而增大,与峰值应力相似,动态增长因子与最大应变率之间也有良好的线性关系.
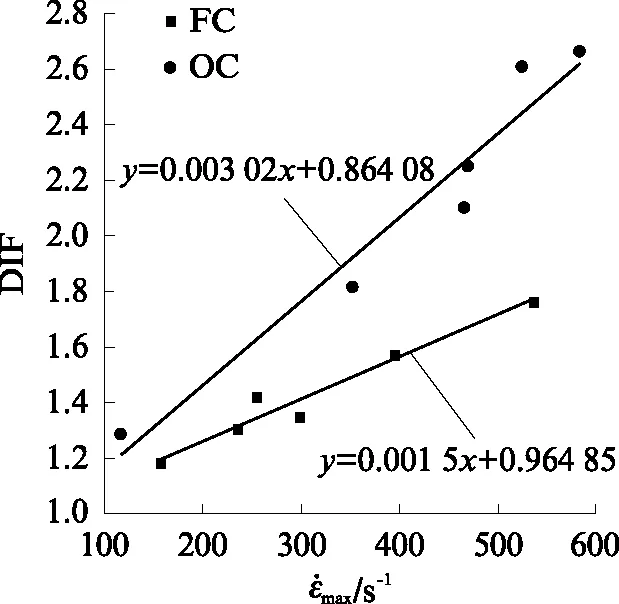
图5 动态增长因子随最大应变率变化趋势Fig.5 Trend of dynamic increase factor with maximum strain rate
3 动态本构关系
由于泡沫混凝土材料的特殊性,受冲击载荷后,其应力-应变曲线上下波动较大,即使采用灵敏系数极高的半导体应变片及相应的脉冲整形技术,曲线的波动也较大[5,8].根据混凝土类材料的性质,线弹性阶段曲线的波动实际上可以归结为电磁干扰信号,其整体趋势是可信的.为了归纳宏观试验结果,本文建立了1个能较好反映峰值应力前动态应力-应变关系的近似等效本构模型,首先对峰值应力前动态应力-应变曲线进行降噪处理,处理后的曲线如图6所示.
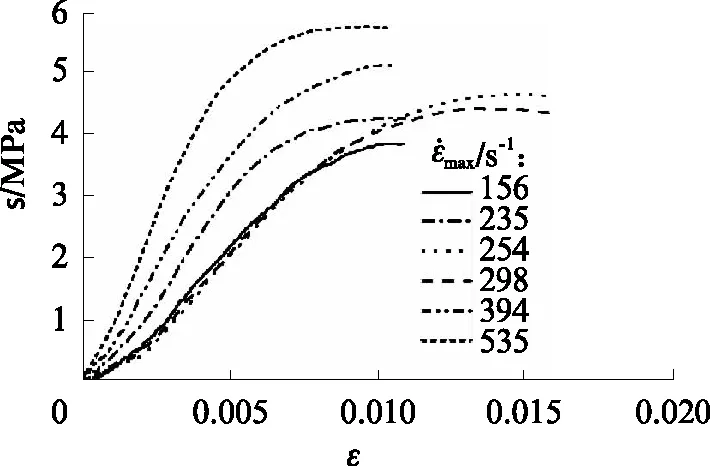
图6 降噪处理后峰值应力前动态应力-应变曲线Fig.6 Dynamic stress-strain curves before peak stress after noise reduction
考虑到泡沫混凝土的应变硬化和应变率硬化等力学行为,采用朱-王-唐非线性黏弹性本构方程[9]可以对泡沫混凝土的动态力学性能进行较好的表达,朱-王-唐本构方程为:
(3)
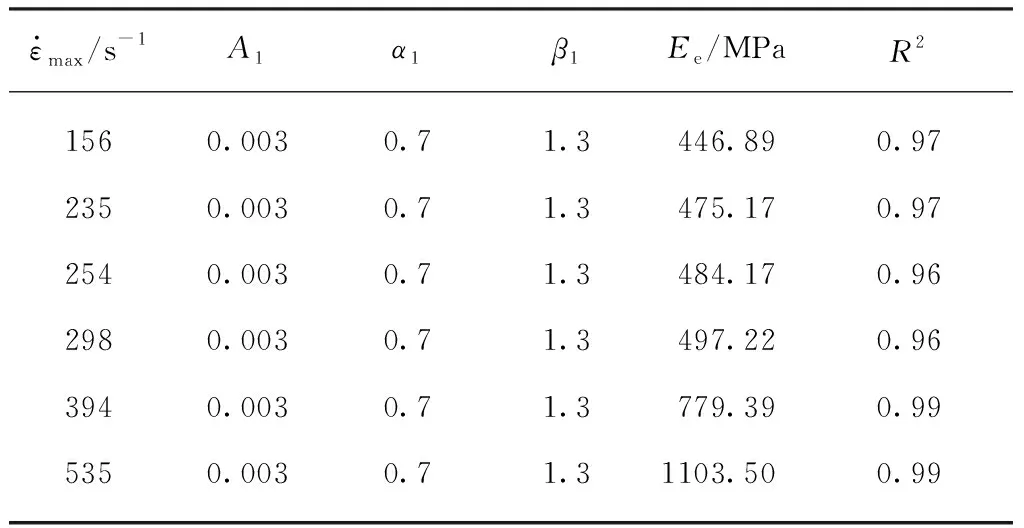
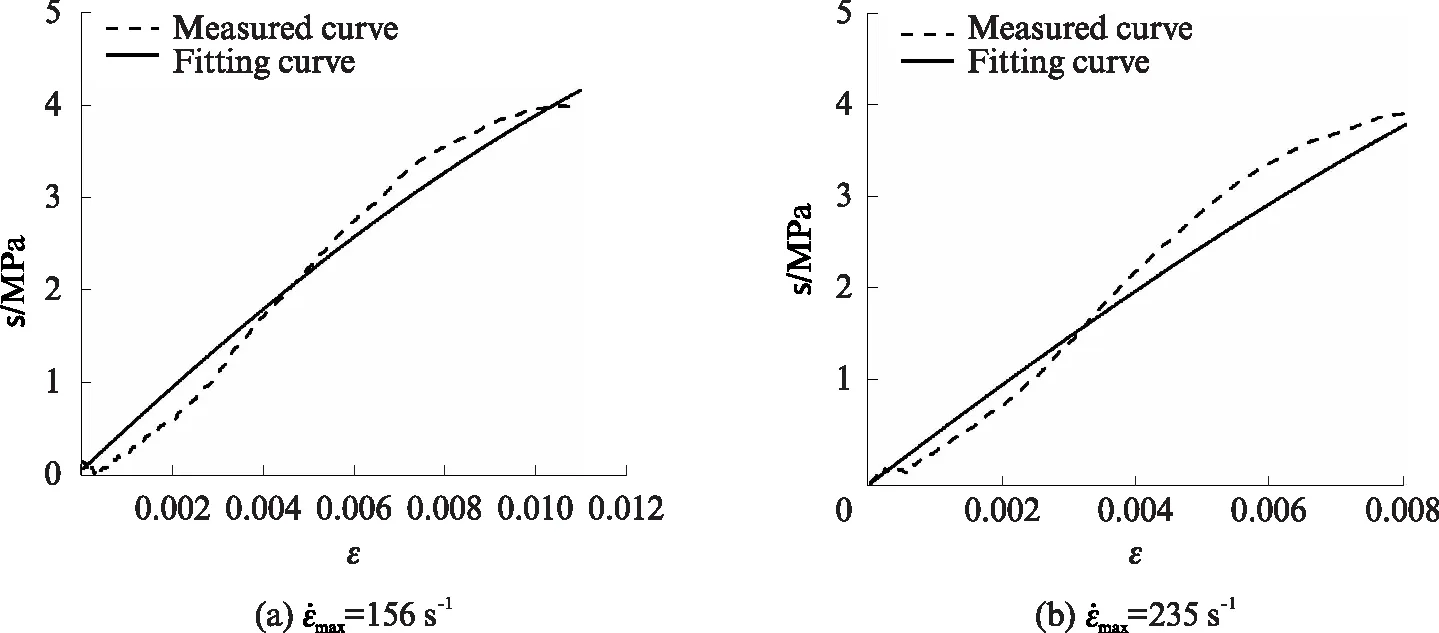
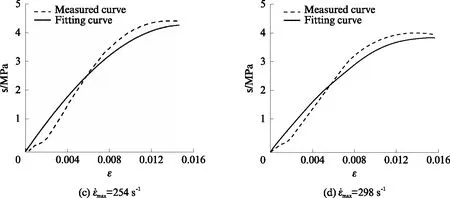
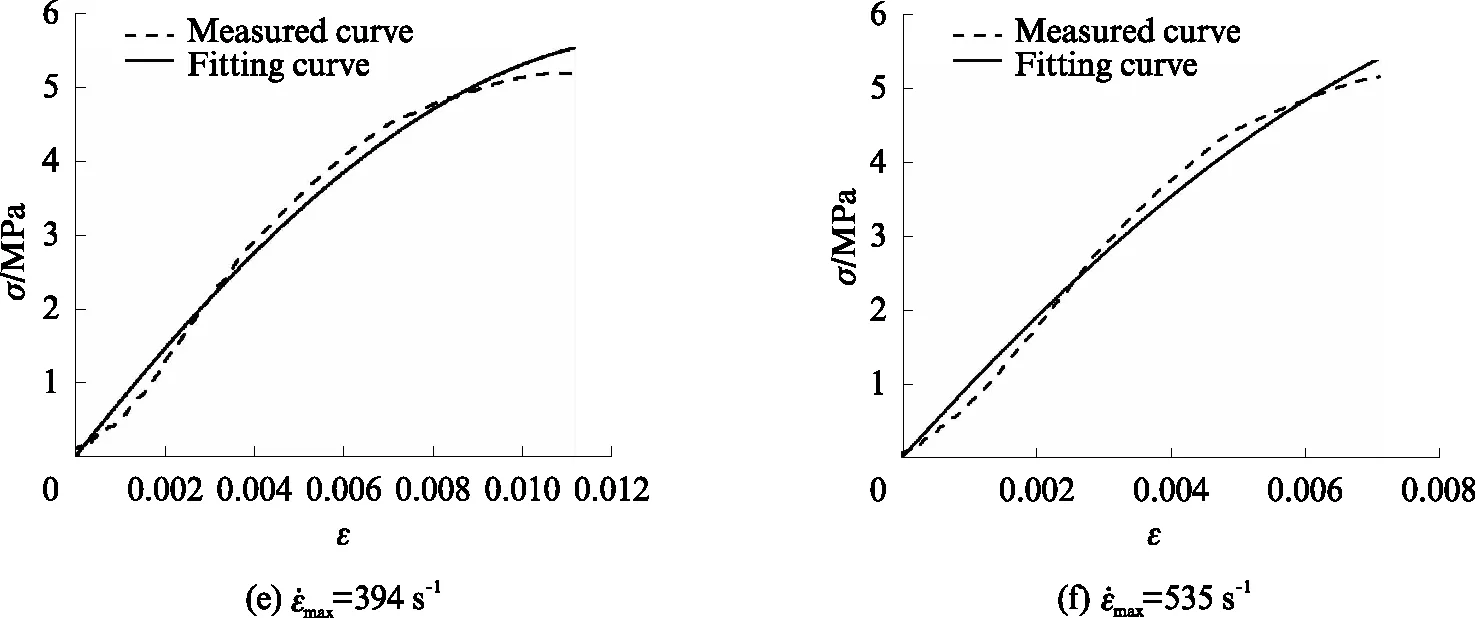
式中:E0、α、β为非线性弹簧弹性常数;E1、E2分别为低频和高频Maxwell体的弹性模量;θ1、θ2为松弛时间;τ为时间,0<τ 针对泡沫混凝土在冲击载荷下的实际力学响应和朱-王-唐本构方程中各项所代表的物理意义,对朱-王-唐本构方程做下述改进: (1)方程式的第1项,即E0ε+αε2+βε3,表示冲击加载时材料的平衡态力学响应,与应变率无关.由试验结果可知,泡沫混凝土应变很小,根据文献研究[8-13],可以将非线弹性部分看作线性,相应地,将朱-王-唐本构方程中的非线性弹簧简化为线性弹簧.即可将三次多项式简化为一次线性多项式,则第1项的简化形式为E0ε. (4) 可将其中2个并联的线性弹簧(E0、E1)等效为1个弹簧(Ea),等效后的方程为: (5) (3)泡沫混凝土为非均质材料,其内部存在着微裂纹、微空洞等诸多缺陷,且这些缺陷的分布都是未知的,在研究泡沫混凝土的动态本构关系时应当考虑损伤因素.由于泡沫混凝土中微观缺陷的分布规律极其复杂且离散性很大,本文采用连续损伤力学方法来解决,即将泡沫混凝土材料假设为连续介质,引入宏观损伤变量D来表征泡沫混凝土的损伤程度.根据Lemaitre应变等效原理,得到泡沫混凝土含损伤本构方程的基本形式: (6) 于是泡沫混凝土的动态本构方程可以用如下形式给出: (7) (8) 根据式(8)对不同最大应变率下泡沫混凝土峰值应力前动态应力-应变曲线进行拟合,拟合参数如表3所示,拟合曲线如图7所示.由表3和图7可知,拟合曲线与实测曲线有较好的一致性,说明本文构建的等效本构方程可以反映泡沫混凝土峰值应力前动态应力-应变关系. 表3 不同应变率下拟合曲线参数 图7 泡沫混凝土的试验和拟合动态应力-应变曲线Fig.7 Measured and fitting dynamic stress-strain curves for foam concrete (1)泡沫混凝土在冲击载荷作用下具有显著的应变硬化和应变率硬化特性,其峰值应力与最大应变率近似成正比例关系;峰值模量随最大应变率增长而增加;在初始加载阶段泡沫混凝土宏观上具有较好的线弹性变形特性,随着加载继续,内部裂纹逐渐扩展,泡沫混凝土切线模量逐渐下降. (2)因泡沫混凝土内部多孔结构的特殊性,其应力-应变曲线上下波动较大,在破坏阶段尤为明显;在应变软化阶段,应力值并没有快速下降至完全丧失承载力,而是形成了1个较高的应力平台,并且最大应变率越高,应力平台越长、越显著.从破坏层面分析,在较低最大应变率下,泡沫混凝土主要呈均匀压实破坏;在较高最大应变率下,则呈现逐层塌落的破坏形式. (3)冲击载荷作用下泡沫混凝土的动态增长因子-应变率拟合曲线斜率小于普通混凝土,即虽然2种混凝土都表现出了显著的应变率效应,但泡沫混凝土对应变率的敏感性不及普通混凝土. (4)基于泡沫混凝土的动态力学特性,通过改进朱-王-唐本构方程,在宏观上构建了反映泡沫混凝土峰值应力前动态应力-应变关系的等效本构方程,通过数值拟合的方式得到了本构方程参数,拟合曲线与实测曲线具有较好的一致性.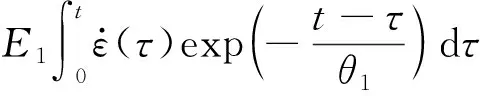
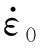
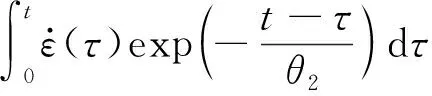
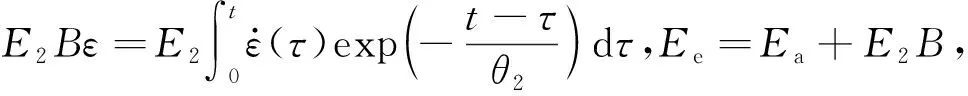
4 结论
