东北地区稻谷储藏期间脂肪酸含量的预测模型

王启阳，吴文福，兰天忆

（吉林大学生物与农业工程学院，长春130022）

0 引 言

粮食储备是保障国家粮食安全的重要物质基础。据统计，2018年中国共有标准粮食仓房仓容6.7亿t[1]，如何保证粮食储藏过程中的品质显得尤为重要。粮食储藏过程中，谷物中脂肪酸含量是其品质变化的敏感性指标，常被用来衡量谷物变质程度[2-4]。谷物在储藏过程中游离脂肪酸含量随时间增加，品质也会随之下降，到一定程度将不能食用。因此，研究谷物中脂肪酸含量的变化规律意义重大。

为了研究谷物中脂肪酸含量的变化规律，国内外众多研究人员做了大量研究。Park等将水稻置于不同温度条件下储藏一定时间，结果表明温度对水稻储藏期间脂肪酸含量的影响非常显著[5]。杨慧萍等研究了不同温度和水分条件下粳稻谷的脂肪酸变化规律，并建立了稻谷脂肪酸值与气味值的回归方程[6]。De Alencar等研究了大豆在不同储存温度下品质的变化规律，建立了大豆脂肪酸值与储存时间的方程，并对方程进行了显著性分析[7]。Dong等根据大豆储藏过程中脂肪酸值的变化对大豆的保质期进行预测[8]。宋伟等分析了小麦储藏积温与游离脂肪酸关系，并建立了储藏积温与小麦脂肪酸的线性回归方程[9]。上述方法通过对品质变化规律进行曲线拟合，得到其品质变化方程，进而预测谷物中脂肪酸含量。

近年来机器学习（machine learning,ML）与大数据技术的出现，为储粮安全提供了新的思路，得到广泛的应用。孙勃将BP神经网络实现了储粮宜存概率的预测，并基于此设计了一套粮食储存品质预测软件[10]。Liu等对不同储粮因素引起的粮食损失进行了分析和预测，并建立了基于决策树算法的粮食损失预测模型[11]。张德贤等提出了基于SVR的粮仓储粮重量检测模型[12]。Shen等利用深度神经网络提出了一种对储粮害虫进行检测和识别的方法，取得了较好的效果[13]。然而，却鲜有将机器学习方法用于稻谷脂肪酸含量预测的报道。

综上所述，本文利用机器学习算法预测稻谷在储藏过程中的脂肪酸含量（以KOH计）。采用主成分分析方法对采集所得数据进行筛选和压缩，从中选取若干对稻谷脂肪酸含量具有最佳解释能力的关键因子，用较少的变量代替原来较多的变量与脂肪酸含量之间进行回归建模和验证；将选择的关键预测因子分别输入到多元线性回归（multiple linear regression，MLR）、人工神经网络（artificial neural network，ANN） 、 支 持 向 量 回 归（support vector regression，SVR）、最小二乘支持向量回归（least square support vector regression， LSSVR）等模型，并采用均方根误差等指标分析各模型的预测性能，探讨稻谷脂肪酸含量预测的最优模型算法，为科学储粮提供了依据。

1 材料与方法

1.1 数据收集与处理

1.1.1 数据采集

在本文研究工作中，试验数据来自东北地区的5个储备粮粮库，其中黑龙江3个粮库、吉林省1个粮库、辽宁省1个粮库，共包含35个粮仓。粮库作业人员定期在粮仓中扦样，送至当地检测站进行相关数据检测，其中脂肪酸含量检测方法按照国家标准GB/T 29405-2012《粮油检验谷物及制品脂肪酸值测定仪器法》中规定的光度滴定仪法进行，水分检测按照国家标准GB/T 5497-1985《粮食、油料检验水分测定法》中规定的定温定时烘干法进行。粮温均采用电子检温系统检测并保存记录。

1.1.2 粮温数据处理

由于设备故障、天气及人为因素等影响会造成粮温数据异常或缺失等情况，需要对收集到的粮温数据进行处理：首先将粮情温度数据中数值过大、过小及乱码的数据清除；其次，采用线性插值的方法补全缺失的粮温数据[14]。

1.1.3 储藏有效积温

储粮温度是影响储粮安全的关键因素[15]，对粮食中脂肪酸含量的影响显著[16]，原因是温度不仅影响粮食中现有霉菌的种类，也影响所形成代谢产物的种类和产量，从而导致粮食脂肪酸含量的变化[17-19]。因此，本文引入储藏有效积温用于稻谷脂肪酸预测。当温度高于某一温度值时，生物体开始发育生长，因其生长还需一定的时间，将这一段时间温度的积累称为有效积温[20]。粮食中生物与微生物的大量活动能够导致粮食发热，而粮食温度高低也直接影响粮食中生物与微生物的活动状况，研究表明储粮温度为-8℃时仍能检测到霉菌[21]，因此本文取-8℃为储藏积温的相对0点计算有效积温，计算公式为

式中K为有效积温，℃·d；Ti为实测储粮温度，℃；N为计算储藏积温的时间，d；n储粮总时间，d；T0为储藏积温相对0点。

1.1.4 数据归一化

标准归一化处理可使每个数据特征的量纲相同，提高算法的训练速度和精度，研究表明将输入数据归一到（0，1）范围内的性能表现出优于原始输入数据的性能[22]，因此，有必要在建立预测模型前对原始数据进行归一化处理。本文先将原始数据归一化处理，最后将模型输出值反向转换为原始比例，归一化公式为

式中xi和分别为原始数据和归一化后的数据，xmax和分别为数据样本的最大值和最小值。

1.2 研究方法

1.2.1 主成分分析

谷物中脂肪酸含量受生物、非生物等多种因素影响，因此模型输入变量的选择非常重要，它直接影响模型的预测精度。本文所收集的因素从个体来说，都与谷物脂肪酸含量有相关关系，但建立模型时选择变量过多一方面增加了计算量和分析问题的复杂性，另一方面也存在信息的重叠现象，因此需要选择关键影响因子作为模型输入变量。主成分分析（principal component analysis，PCA）是一种重要的数据统计方法，其利用降维的思想把多指标转化为少数几个综合指标，在保留原始数据主要特征前提下，根据实际需要从中选取出几个较少的变量对问题进行定量分析，减少输入数据维度[23]。

1.2.2 预测模型统计

1）多元线性回归

多元线性回归（MLR）主要是研究1个因变量与2个或2个以上自变量之间的关系。它用于根据2个或多个其他变量的值预测变量的值。一个包含k个预测因子（自变量）和一个响应变量（因变量）的线性回归模型可以表示为

式中Y为响应变量，Xk为预测因子，ε0为模型的残差项，β0、β1、β2、…、βk为回归系数。

2）人工神经网络

人工神经网络（ANN）简称神经网络，是基于生物学中神经网络的基本原理，在建模过程中模拟大脑的互联性。人工神经网络的目标是通过一些内部计算从输入值计算输出值，它能够从实例中学习实值、离散值和向量值函数，并且对训练数据中的错误保持较强的鲁棒性[24]。本文建立3层人工神经网络模型，包括1个输入层、1个隐含层和1个输出层。试验过程使用的梯度优化器为Adam，隐藏层激活函数选择sigmoid，输出层为ReLu函数，并设置epoch为200。

3）支持向量回归

支持向量机（support vector machine，SVM）是由Vapnik等提出的一种机器学习方法，通过非线性映射将自变量映射到高维的特征空间，在高维特征空间中寻找一个最优分类超平面，使得所有训练样本距离该最优分类面的误差最小[25]。支持向量回归（SVR）假设模型输出与真实值之间可被容忍最多为ε的偏差，即仅当模型输出与真实值之间的差别绝对值大于ε时才计算损失，是支持向量机在回归问题上的应用模型[26]。

4）最小二乘支持向量回归

最小二乘支持向量回归（LSSVR）是SVR的一种改进算法，利用二次损失函数取代传统支持向量机中不敏感的损失函数，将标准支持向量机中的不等式约束条件转化成等式约束，并将损失函数由误差和转变为误差的平方和，使求解过程由二次寻优问题转化为线性方程组的求解，具有运算简单、收敛速度快的优点[27-28]。

1.2.3 SVR和LSSVR模型参数调节方法

1）核函数的选择

支持向量机常用的核函数有径向基核函数（RBF）、多项式核函数、Sigmoid核函数及线性核函数，引入核函数的目的是代替高维特征空间的内积运算，避免出现维数灾难[29]。本文选择RBF，其函数表达式为

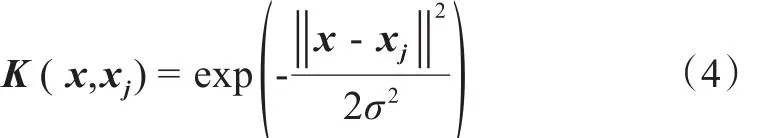
式中x为m维输入向量；xj为第j个径向基函数的中心，与x具有相同的维数；σ为核函数的宽度参数；为向量x-xj的范数，表示x与xj之间的距离。

2）粒子群优化算法

粒子群优化算法（particle swarm optimization，PSO）[30]是Kennedy和Eberhart在1995年提出的一种随机优化技术，其思想源于对鸟类群体觅食行为研究，通过群体中个体之间的协作和信息共享来寻找最优解，目前，已经广泛应用在约束优化和多目标优化等领域[31-32]。PSO算法具有简单易行、鲁棒性好、收敛速度快等优点[33]。为了提高SVR和LSSVR模型的预测性能，本文利用PSO算法确定训练模型的超参数，取平均绝对百分误差作为适应度函数，并采用10折交叉验证。

1.2.4 模型评价指标

为了全面的评价储粮过程中脂肪酸变化预测模型的性能，本文采用多种评价指标：均方根误差（root mean square error，RMSE）、平均绝对误差（mean absolute error，MAE）、平均绝对百分误差（mean absolute percentage error，MAPE） 和决定系数 （coefficient of determination，R2），各评价指标表达式如下

式中fi为预测值；yi为测试样本的真实值；yˉ为测试样本的平均值；N为测试样本集数量。

1.2.5 平台和环境

本研究仿真试验所使用的计算机的配置如下：处理器为Intel(R)Core(TM)i5-4200M，CPU频率为2.5 GHz；内存为8.00 GB；操作系统为Windows 10（64-bit）；程序设计语言为python 3.7（64-bit），集成开发环境为Anaconda 3。

2 结果与分析

2.1 不同储藏参数统计及Pearson相关性分析

经过计算处理后共得到201条稻谷储藏数据，每条数据包含10个储藏参数：入仓月份、初始水分、初始脂肪酸含量、检测水分、储藏有效积温、储藏时间、检测粮温、检测仓温、检测月份和检测脂肪酸含量，各参数统计数据见表1。

表2为不同预测因子的相关性分析。由表2可知，检测水分与储藏有效积温、储藏时间以及检测粮温呈极显著负相关（P＜0.01），而与初始水分呈极显著正相关（P＜0.01）；储藏有效积温与储藏时间呈极显著正相关（P＜0.01）；检测粮温与检测仓温、检测月份呈极显著正相关（P＜0.01）。由此可见，不同预测因子之间存在不同程度的相关性，预测因子间存在信息重叠，直接利用进行脂肪酸含量预测会导致预测结果出现偏差。因此，需要用主成分分析法将众多具有一定相关性的预测因子剔除，再用选择的关键预测因子对稻谷脂肪酸含量进行预测，提高预测结果的可靠性。

表1 稻谷储藏参数统计Table 1 Statistics on storage parameters of rice

2.2 关键预测因子选取

采用SPSS软件对入仓月份、初始水分、初始脂肪酸含量、检测水分、储藏有效积温、储藏时间、检测粮温、检测仓温、检测月份9个预测因子进行主成分分析，探寻影响脂肪酸含量的关键因子，分别得到各主成分的特征值及累积贡献率，结果见表3。以特征值大于1.0的原则提取4个主成分，累计贡献率为80.603%，可代表原始数据的大部分信息，经标准化后的因子负荷矩阵如表4所示。

表2 不同储藏因子间的相关系数矩阵Table 2 Correlation coefficient matrix between different storage factors

由表3和表4可知，第1主成分包含了原始信息量的31.321%，其大小主要由检测粮温、检测仓温和检测月份决定，命名为温度因子；第2主成分包含了原始信息的23.719%，其大小主要由储藏有效积温和储藏时间决定，命名为时间因子；第3主成分包含了原始信息的14.284%，其大小主要由初始水分决定，命名为水分因子；第4主成分包含了原始信息的11.279%，其大小主要由初始脂肪酸含量决定，命名为初始因子。

结合相关性分析和因子分析的结果，在温度因子中，3个代表因子极显著相关，检测粮温比检测仓温更具有代表性，用以代替该因子；同样，在时间因子中，2个代表因子极显著相关，储藏有效积温更为客观影响脂肪酸含量的变化，用以代替该因子。因此，本文选择初始脂肪酸含量、初始水分、储藏有效积温、检测粮温4个预测因子作为稻谷脂肪酸含量变化的主要影响因子，即用该4个预测因子预测稻谷脂肪酸含量。

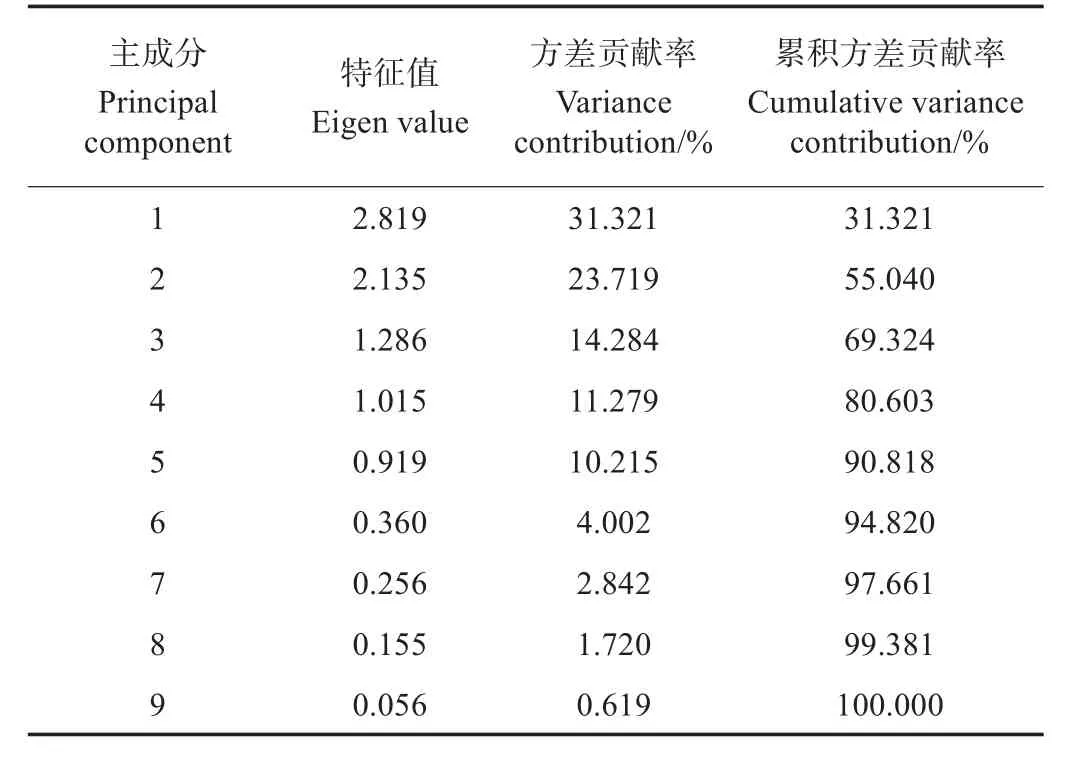
表3 特征值及累积贡献率Table 3 Eigen value and cumulative variance contribution

表4 因子负荷矩阵Table 4 Component matrix

2.3 SVR和LSSVR模型参数优化

1）SVR模型参数优化

SVR模型参数设置：粒子群体的大小为30，惯性权重ω取初始值为0.9，加速度常数取c1=c2=2，最大迭代次数为100，判断终止精度为10-4，正则化参数C、不敏感参数ε及核函数参数γ的初始搜索范围分别设定为[1，1000]、[0.001，0.1]和[0.1，10]，搜索过程中如果超过边界则设为边界值。通过PSO算法得到SVR模型的最优参数正则化参数C、不敏感参数ε及核函数参数γ分别为569.3、0.05、2.7。

2）LSSVR模型参数优化

LSSVR模型参数设置：粒子群体的大小为30，惯性权重ω取初始值为0.9，加速度常数取c1=c2=2，最大迭代次数为100，判断终止精度为10-4，正则化参数C、和核函数参数γ的初始搜索范围分别设定为[1，1000]和[0.0001，1]，搜索过程中如果超过边界则设为边界值。LSSVR模型的最优超参数正则化参数C’和核函数参数γ’分别为1000.0和0.003。

2.4 仿真结果分析

将经过归一化预处理后的201条样本数据随机划分为训练集和测试集，其中训练集样本数占总样本的80%，剩下的20%样本用于模型性能测试。将划分好的数据集分别输入到MLR、ANN、SVR、LSSVR 4种模型，经过仿真试验得到模型的测试集误差曲线如图1所示。由图1可知，在所测试的41个样本中，LSSVR和MLR2种模型的预测误差波动较小，预测误差的范围分别为：-0.759～0.764 mg/100 g，-0.764～0.802 mg/100 g；ANN和SVR2种模型的预测误差波动较大，预测误差的范围分别为：-0.787～0.902 mg/100 g，-0.814～0.879 mg/100 g。

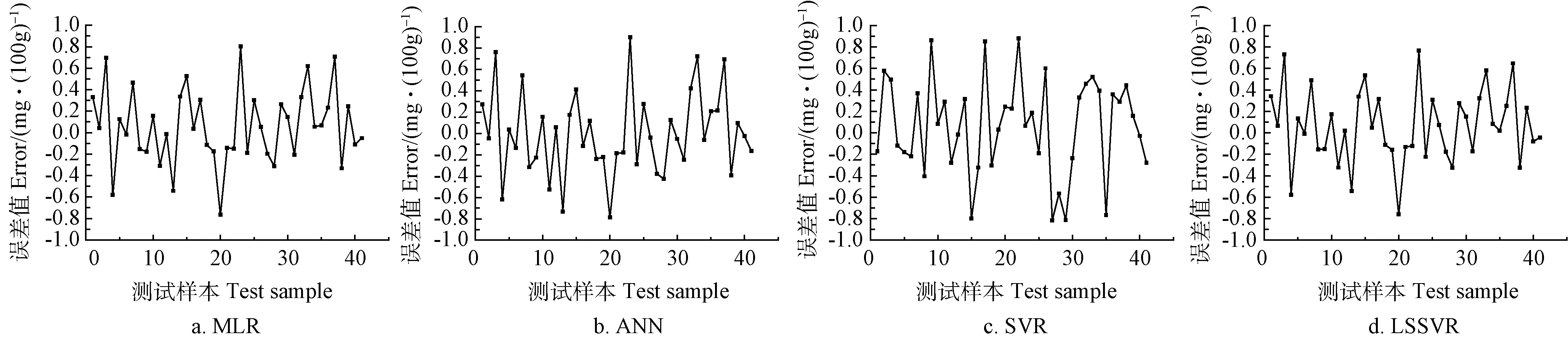
图1 不同模型预测结果的误差Fig.1 Errors of predicted results of different models

表5给出了4种模型在测试集上预测性能的指标统计结果。从表5可得，MLR和LSSVR对稻谷脂肪酸含量预测的MAPE相近，分别为1.615%和1.604%，表明LSSVR得到的结果要略优于MLR；ANN对稻谷脂肪酸含量预测的MAPE为1.708%，相较于LSSVR而言，MAPE值增加了0.176%，表明ANN的预测能力要次于LSSVR，即LSSVR的预测精度更高；此外，还可看出LSSVR模型的MAPE要明显低于SVR。对比4种预测模型，LSSVR的预测效果明显优于SVR和ANN，略优于MLR，说明LSSVR预测精准度最高，该回归模型的决定系数R2、MAE、MAPE、RMSE分别为0.911、0.275 mg/100 g、1.604%、0.348 mg/100 g。试验结果表明，LSSVR和MLR对稻谷脂肪酸含量预测达到了较为理想的效果，预测精度高，可以用于储藏期间稻谷的脂肪酸含量的预测。

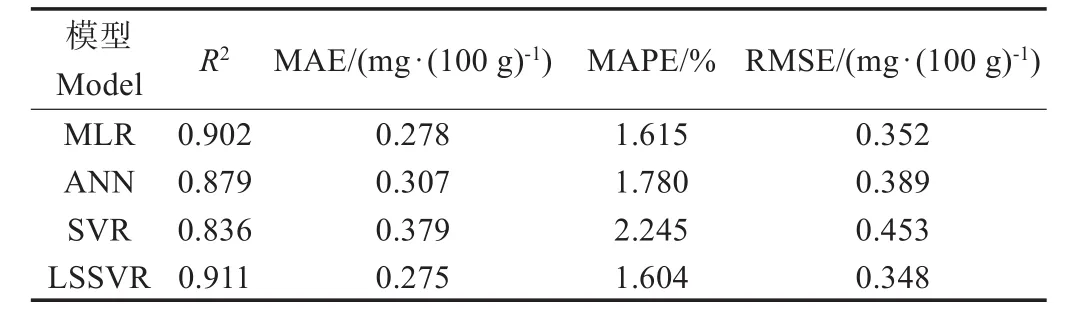
表5 不同模型预测性能对比Table 5 Comparisons of predictive performances of different models

3 结论与讨论

本文基于机器学习中多种方法，结合实际储藏数据对稻谷脂肪酸含量预测方法进行了研究，结论如下：

1）利用主成分分析方法确定了初始脂肪酸含量、初始水分、检测粮温、储藏有效积温4个预测因子作为脂肪酸含量的主要影响因子。

2）将选择的关键预测因子分别输入到多元线性回归（multiple linear regression，MLR）、人工神经网络（artificial neural network， ANN）、 支 持 向 量 回 归（support vector regression，SVR）、最小二乘支持向量回归（least square support vector regression，LSSVR）模型进行了仿真试验。在测试集中LSSVR模型预测结果的决定系数R2、MAE、MAPE、RMSE分别为0.911、0.275 mg/100 g、1.604%、0.348 mg/100 g，略优于MLR，明显优于ANN和SVR。仿真结果表明，LSSVR和MLR对稻谷脂肪酸含量预测精度高，达到了较为理想的效果，可以用于储藏期间稻谷的脂肪酸含量的预测。

因获取储粮数据数量有限，下步可尝试扩大训练样本和测试样本数量，使用更多的数据训练MLR、ANN、SVR、LSSVR模型。同时可将天气、湿度、品种、粮仓状况等因素纳入特征范围，进一步提高预测精度。