基于流形光谱降维和深度学习的高光谱影像分类

师 芸，马东晖，吕 杰，李 杰，史经俭

（西安科技大学测绘科学与技术学院，西安710054）

0 引 言

高光谱影像（hyperspectral image，HSI）具有丰富的光谱信息，在林业、农业、地学等领域具有广泛的应用前景，对高光谱影像进行分类是获取高光谱影像信息的重要手段之一[1-3]。为解决高光谱影像分类中存在的小样本、多维度、相关性和非线性等问题，国内外研究人员对此进行了大量研究[4]，按照标记样本数量的不同可分为监督分类、无监督分类、半监督分类。监督分类如神经网络（neural networks，NN）、支持向量机（support vector machine，SVM）[5]和决策树 （decision tree）[6]等，都取得了较好的结果。无监督分类常用的方法有K均值聚类（k-means clustering algorithm）[7]、 谱 聚 类 （spectral clustering）[8]等。半监督分类是监督分类与无监督分类相结合的一种方法，De Morsier等[9]提出了一种基于空间－光谱标签传播的半监督分类方法，使用支持向量机作为分类器，参数对分类结果影响较大。传统分类方法虽然取得了一定的效果，但难以提取高光谱影像的深层特征。

深度学习作为机器学习的一个分支，在图像分类和地物识别等领域均取得了优异的成绩[10-11]。Lecun等[12]提出著名的LeNet-5模型，首次应用了卷积神经网络（convolutional neural networks，CNN），但受制于计算机硬件水平，当时并没有引起重视。2012年Krizhevsky等[13]提出的Alexnet模型在ImageNet竞赛中取得2个第一名，由此引发了研究人员的极大关注。近年来，深度学习在高光谱遥感影像分类中表现出优异的性能。Chen等[14]首次将深度学习应用于高光谱数据分类，提出一种堆栈自编码器（stacked autoencoder，SAE），对高光谱影像进行主成分分析后，将空间信息和光谱信息输入SAE进行分类，取得了较高的精度，但SAE采用了全连接的方式，导致了网络参数过多，训练用时过长。Romero等[15]利用深度卷积神经网络对高光谱影像进行分类，采用了一种逐层贪婪预训练的策略，学习输入图像的分层稀疏表示，与单层网络相比，深层网络能更好地提取空间－光谱特征，但同时也存在过拟合等问题。Li等[16]提出一种基于像对特征（pair of pixel feature，PPF）高光谱影像分类方法，利用CNN从高光谱影像中提取像对模型并构建深层像对特征，采用联合分类器进行分类，有效改善了带标记的训练样本的不足问题，进一步提升了模型的特征提取能力，但牺牲了运算资源和运算时间。上述算法虽然表现出优异的分类性能，但同时也存在模型较为复杂、运算时间过长等问题。如何提高高光谱影像分类精度的同时保证运算效率，是当前高光谱影像分类领域亟待解决的问题。

高光谱影像各个波段之间的数据冗余降低了分类的精度[17]，增加了分类用时。流形学习（manifold learning）作为机器学习领域的一个热点研究方向，旨在从原始高维数据中恢复低维流形结构，并求出相应的嵌入映射，以实现维数约简[18]。根据投影方式的不同可将流形学习分为线性流形学习算法和非线性流形学习算法。线性算法如线性判别分析（linear discriminant analysis，LDA）算法，是一种监督学习的降维方法，核心思想是投影后类内方差最小，类间方差最大[19]。非线性算法如局部线性嵌入（locally linear embedding，LLE）算法，假定高维空间任意点都可以由其邻域点和对应权值表示，可以在低维空间中恢复其局部线性特征从而实现 降 维[20]； 随 机 邻 域 嵌 入 （stochastic neighbor embedding，SNE）算法通过将数据点之间的欧氏距离转化为条件概率来在低维空间中表示其高维相似性[21]；t分布随机邻域嵌入（t-distribution stochastic neighbor embedding，t-SNE）算法是对SNE算法的改进，将高维空间模拟成高斯分布，将低维空间模拟成t分布，t分布长尾的特性使得数据点能够在低维空间中更均匀地分布[22]。近年来，相关学者将上述算法应用于高光谱影像降维中，Wang等[23]在LDA算法的基础上提出一种局部自适应判别分析（locality adaptive discriminant analysis，LADA）算法，对高光谱数据的局部流形结构具有更好的自适应性。Tang等[24]提出一种局部线性嵌入稀疏表示（locally linear embedding sparse representation， LESR）算法，在LLE的基础上采用基于流形的稀疏表示算法，利用测试样本在相应稀疏表示中的局部结构来增强相邻样本稀疏表示的平滑性。Zhao和Du[25]提出了一种基于空间－光谱特征的分类框架，采用平衡局部判别嵌入算法进行（balanced local discriminant embedding，BLDE）降维，使用卷积神经网络提取空间特征并分类，在对高光谱影像的试验中取得了较好的结果。

针对高光谱数据分类时存在的运算速度慢、难以充分利用局部特征等问题，本研究提出了一种基于流形光谱特征的高光谱影像分类算法（manifold spectral feature based classification，MSFC），将MSFC应用于Indian Pines、Pavia University和Pavia Center 3个高光谱数据集，降维后采用卷积神经网络进行特征提取并分类，验证所提算法的精度与可靠性。

1 方 法

1.1 t分布随机邻域嵌入算法

t分布随机邻域嵌入算法是一种非线性降维算法，原始高光谱数据处于一个高维流形空间上，利用条件概率分布来描述像点之间的相似性，记高维流形空间内有n个像点的有限高维数据 X={X1,X2,···,Xn}⊂ RD，每个像点的维度为D，记高维像点到低维像点之间的映射为Y={Y1,Y2,···,Yn}⊂ Rd，每个像点的维度为d。

对于每个数据点i和每个潜在的邻近点j，计算条件概率pij，即选择j作为i邻近点的概率，此处定义一个对称的联合概率分布，使得pj|i=pi|j，qj|i=qi|j，则高维空间概率分布pij为

式中pj|i为高维空间中数据点i选择j作为其邻近点的条件概率，n为像点的个数。采用自由度为1的t分布代替高斯分布，作为映射到低维空间中的分布。低维空间概率qij分布为

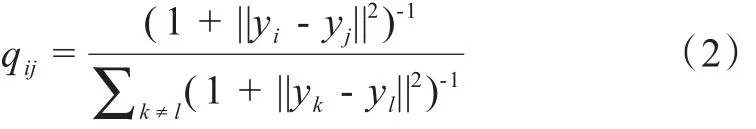
式中yi和yj为高维数据点在低维空间的映射，k为困惑度，对于自由度为1的t分布，在低维映射中较大的点对距离(1+||yi-yj||2)-1与||yi-yj||的平方近似成反比，这使得映射对于距离较远的点，其联合概率表示几乎不受空间规模变化的影响，同一簇内的点聚合的更紧密，不同簇之间的点更加疏远。

1.2 卷积神经网络

卷积神经网络是一种专门用来处理具有类似网格结构的数据的神经网络，通常由若干个卷积层（convolution layer）、池化层（pooling layer）、全连接层（fully connected layer，FC）组成。CNN前几层由卷积层和池化层交替构成，后面由若干全连接层构成[26]。卷积层具有强大的特征学习能力，能够进行层次化的特征提取，卷积层后作用一个整流线性函数（rectified linear units，ReLU）作为激活函数，采用ReLU函数能够将神经网络的训练速度提升数倍，而并不会对模型的泛化准确度造成显著影响[27]。池化层能够缩减模型的大小，同时提高所提取特征的鲁棒性，全连接层作为分类器，以卷积层提取的特征作为输入，将学到的分布式特征表示映射到样本标记空间。

本研究卷积神经网络结构如图1所示。输入网络的训练样本像素大小为37×37×B，其中B是降维后的样本波段数量，在卷积层C1使用500个像素大小为9×9的卷积核对输入的高光谱影像进行卷积操作，之后附加一个激活函数以增加输出的非线性特征，输出像素大小为29×29的500张特征图，然后在池化层P1进行窗口像素大小为2×2的最大池化操作，输出像素大小为14×14的500张特征图，此时特征图尺寸进一步缩小，从而在下一层提取更深层次的特征；在卷积层C2使用像素大小为3×3的卷积对输入图像进行卷积操作，此处附加同样的激活函数，输出像素大小为12×12的500张特征图，在池化层P2进行窗口像素大小为2×2的最大池化操作，输出像素大小为5×5的500张特征图，随后将所有特征图输入全连接层FC1和全连接层FC2中，将之前提取到的所有特征进行综合并分类。

二维卷积运算的过程如图2所示，卷积层的第1个参数称为输入（input），第2个函数为核函数（kernel function），核函数窗口在输入矩阵上依次滑动进行卷积运算，输出得到特征映射（feature map，S）。在CNN中，输入的通常是多维数组的数据，以1张二维图像I作为输入，使用卷积核K在多个维度上进行卷积运算，如式（3）所示

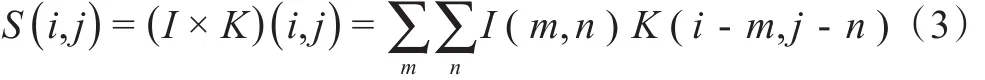
式中m和n为输入图像的尺寸，i和j分别是进行卷积运算的行和列。

图1 卷积神经网络结构Fig.1 Structure of convolutional neural network

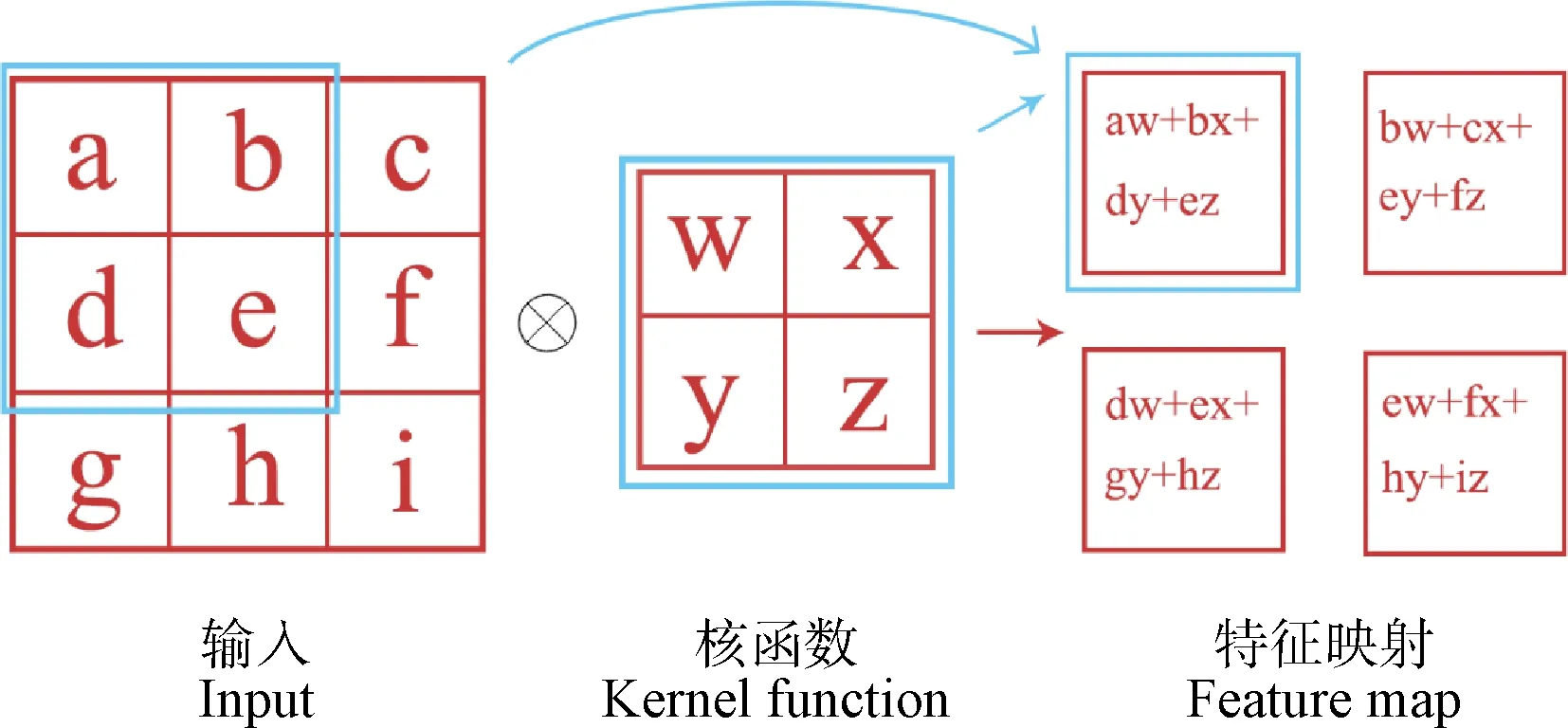
图2 二维卷积运算过程Fig.2 Calculation process of two dimensional convolution

图3为本研究算法流程图，t-SNE算法的目的是对输入的高光谱数据进行维数约简，降低波段间的冗余，确定参数降维维数（reduced dimension，d）和困惑度（perplexity，k）之后对3个数据集进行降维，将降维后的高光谱数据输入卷积神经网络网络，卷积神经网络具有强大的深层次特征提取能力，能够提取高光谱数据的空间－光谱联合特征，在分类结束后进行精度评价。

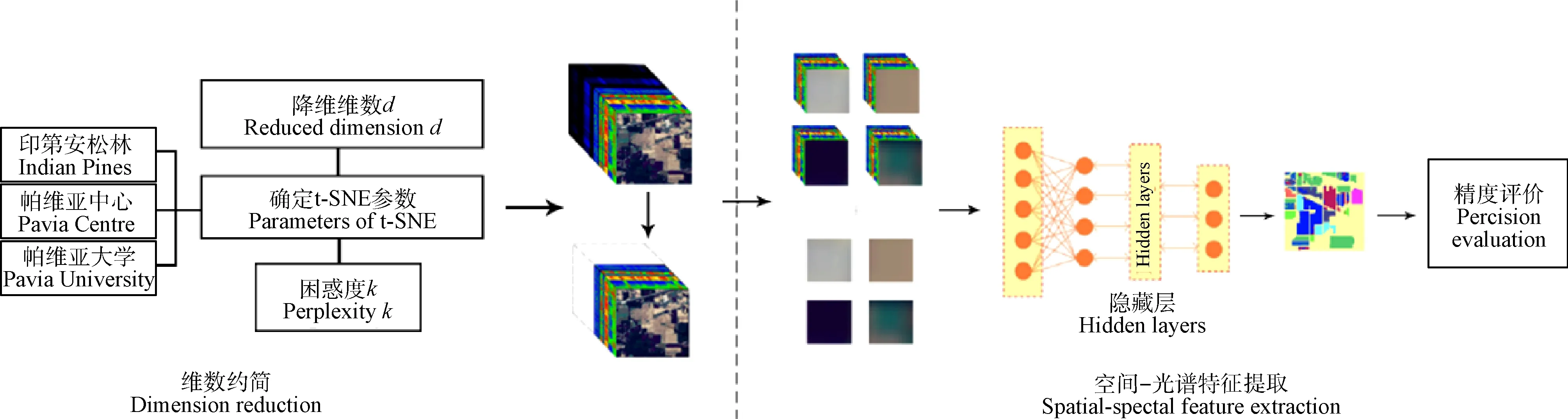
图3 基于流形光谱特征的高光谱影像分类流程图Fig.3 Flow chart of hyperspectral image classification based on manifold spectral feature

2 试验与结果分析

首先，与主成分分析（principal component analysis，PCA）、局部自适应判别分析（locality adaptive discriminant analysis，LADA）、局部线性嵌入稀疏表示（locally linear embedding sparse representation， LESR）和随机邻域嵌入（stochastic neighbor embedding，SNE）等降维算法进行对比，验证本研究降维算法的可靠性，随后对降维后的高光谱数据集进行分类，并与近年来提出的2种降维－分类算法和3种空间－光谱联合分类算法进行对比。在3个公开的高光谱数据集上进行试验，对3个数据集进行降维，将降维后的高光谱数据输入CNN中进行特征提取并分类，采用总体精度（overall accuracy，OA）和Kappa系数作为评价指标。

试验硬件环境为Intel i5 8500 CPU 3.9GHz、NVIDIA GTX 1060 3GB GPU和16GB RAM，软件环境为MATLAB R2014a和基于Python3.5的TensorFlow，使用NVIDIA CUDA 9.0进行GPU加速计算。

2.1 数据准备

本次试验采用了3个高光谱数据集，将3个数据集按训练集75%和测试集25%的比例划分。其中，印第安松林（Indian Pines）数据集是由机载可见光/红外成像光谱 仪 （airborne visible infrared imaging spectrometer，AVIRIS）在美国印第安纳州西北部的试验田获取（表1），像素大小为145×145、波长为0.4～2.5μm，空间分辨率约为18 m，去除覆盖吸水区域的波段后包含200个波段；帕维亚中心（Pavia Center）数据集是由反射光学系统成像光谱仪（reflective optics system imaging spectrometer，ROSIS）获取的意大利北部帕维亚地区的场景（表2），像素大小为1 096×715，去除不可用波段后包含102个波段，空间分辨率约为1.3 m；帕维亚大学（Pavia University）数据集是由ROSIS获取的意大利帕维亚大学的场景（表3），像素大小为610×340，波长为0.43～0.86μm，空间分辨率约为1.3 m，去除吸水区域和低信噪比的波段后包含103个波段。

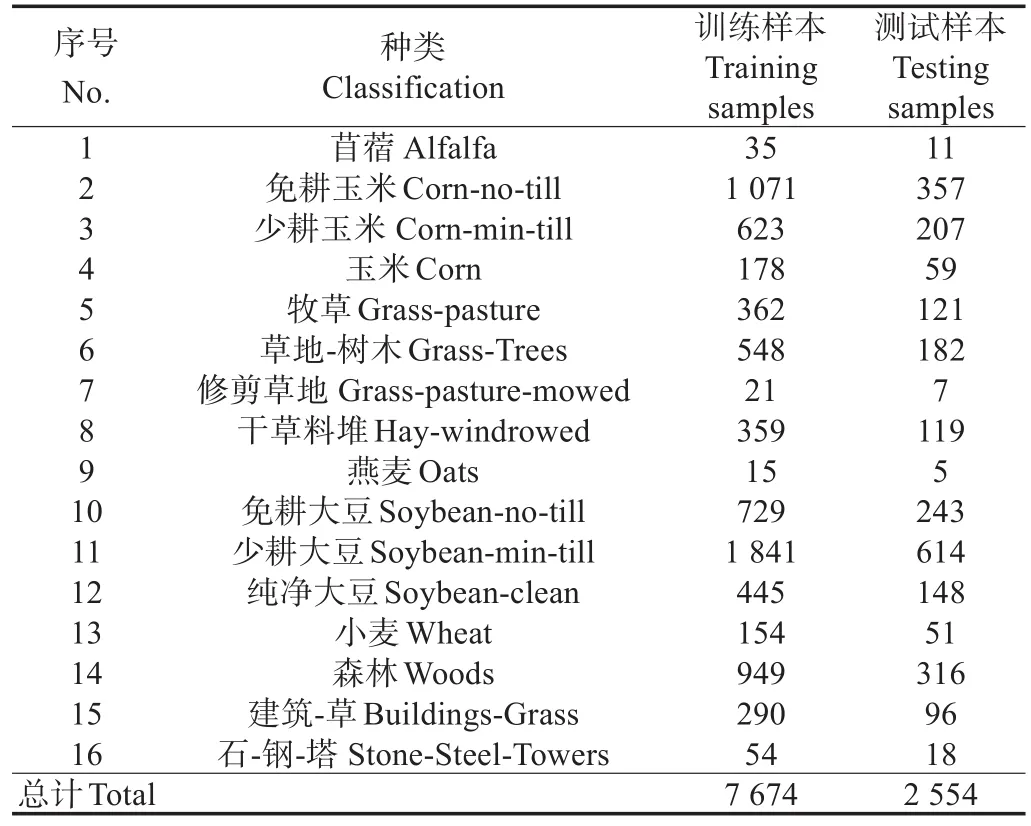
表1 印第安松林数据集地物类别和划分Table 1 Ground classification and division of Indian Pines data set

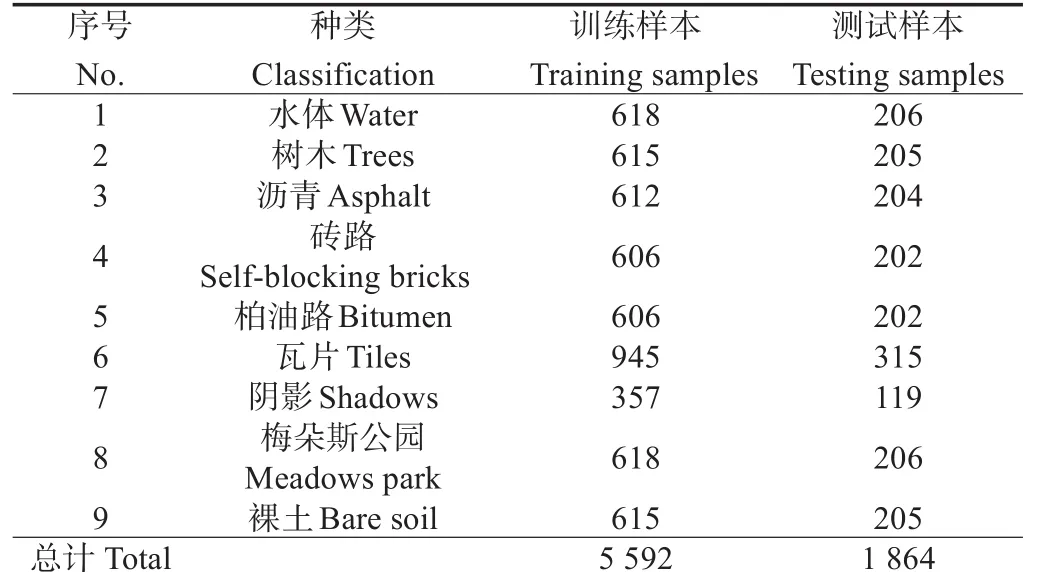
表2 帕维亚中心数据集地物类别和划分Table 2 Ground classification and division of Pavia Center data set

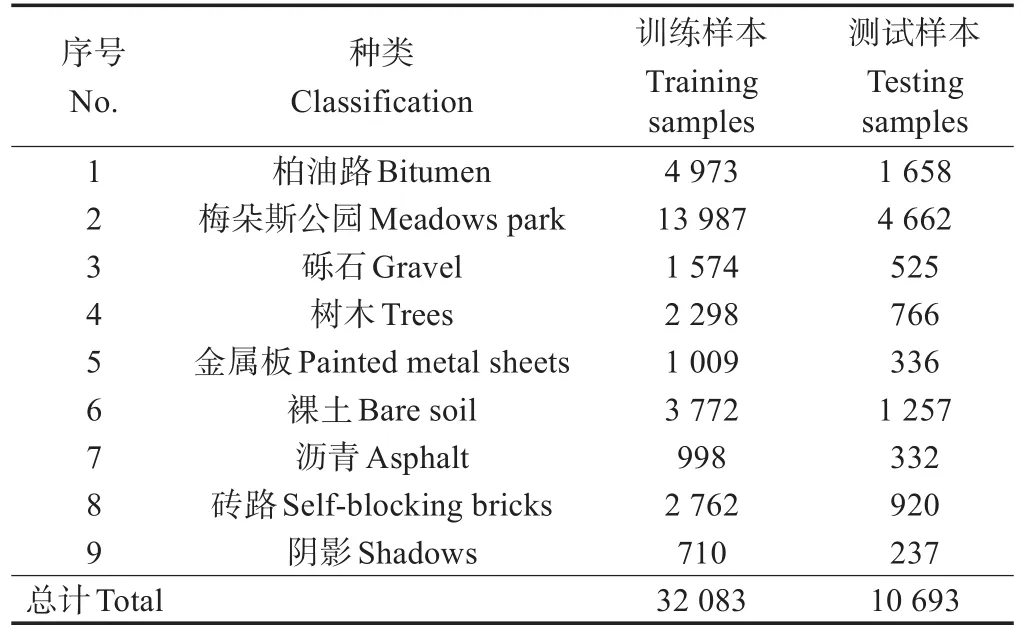
表3 帕维亚大学数据集地物类别和划分Table 3 Ground classification and division of Pavia University data set

2.2 流形学习降维

为验证本研究所提算法的可靠性，与其他4种降维算法进行比对，对Pavia Center数据集进行可视化，每类地物选取100个样本点并投影至二维空间。降维后的散点图如图4所示。PCA和LADA算法类内可分性较差，边缘区域的水体和柏油路分离明显，但其他类别几乎都重叠在一起，原因是这2种算法没有很好的考虑局部特征；对于LESR算法，柏油路、水体和梅朵斯公园3类能够较好地分离，但由于所用高光谱数据庞大，难以顾及所有特征，其余类别仍有重叠，可分性较差；SNE算法的可视化效果有所提升，同一类别的数据点映射至二维空间基本能聚集在一起，但类间可分性较差，边界处的数据点难以划分，存在“拥挤问题”；采用了t分布代替高斯分布的t-SNE算法表现出良好的类内聚集性和类间可分性，明显优于其他算法。

图4 Pavia Center数据集在不同特征空间的散点图Fig.4 Scatter plots of Pavia Center data set in different feature spaces

降维尺度对于分类结果至关重要，为了确定最佳降维尺度d，设置了维度2～30的降维试验，如图5所示，3个数据集的总体精度都与约简的维数近似成正比，显著降低了“休斯（Hughes）”现象的影响，部分算法如LESR和SNE等出现了分类精度随着d先提高后降低的现象，表明d不是越高越好。将Indian Pines数据集d设为20，Pavia Center数据集d设为16，Pavia University数据集d设为18，分别取得了较好的分类结果。算法中另一参数困惑度k与分类精度的关系如图6所示，通过试验最终确定k为30。

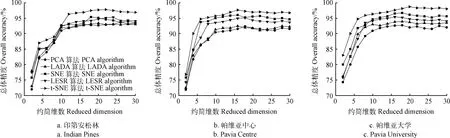
图5 不同数据集在不同降维维度的分类结果Fig.5 Classification of different data sets in different dimensionality reduction dimensions

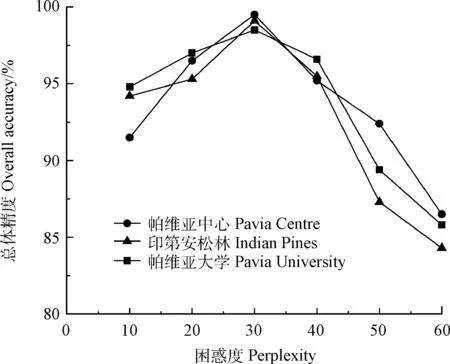
图6 困惑度对t-SNE算法的精度影响Fig.6 Effect of perplexity on the accuracy of t-SNE algorithm

2.3 CNN模型参数的设置

在确定降维维度d和困惑度k之后，将降维后的数据作为输入层，利用CNN进行特征提取并分类。初始学习率为0.01，最大迭代次数4 000次，批处理参数为100，使用AdaGrad算法进行参数更新，网络参数如表4所示。

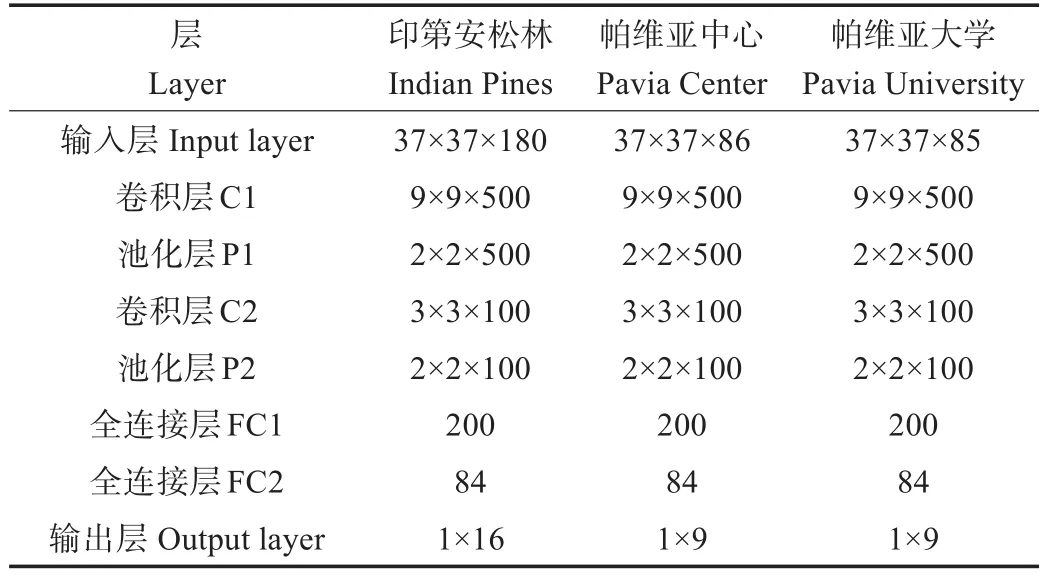
表4 卷积神经网络结构Table 4 Structure of convolutional neural network

2.4 结果与分析

6种算法的总体精度和Kappa系数如表5所示，分类精度如表6～表8所示。

由表5可知，CNN、基于像对特征的卷积神经网络（convolutional neural networks-pair of pixel feature，CNNPPF）和MSFC均为卷积神经网络模型，总体精度和Kappa系数表现均优于其他3种机器学习算法，其中MSFC算法在3个数据集中分类的总体精度和Kappa系数最高，相较于其他5种算法取得了显著的提升，总体精度均在98%以上。横向对比MSFC算法，在Pavia Center数据集上总体精度最高，由于该数据集地物分布较为单一，主要由水体和瓦片组成，混合像元数量相对较少，而地物类型复杂容易产生回混合像元[28]；卷积神经网络的性能依赖于训练样本的数量，Pavia Center数据集的训练样本和测试样本数量分布较为均匀，与其他2个数据集相比，各类地物的训练样本占比均衡，能够更好地发挥深度学习模型的特征提取能力，因此总体精度最高。

由表6～表8可以看出，对于Indian Pines数据集的各类地物，MSFC算法均取得了较高的分类精度，其中作物的分类精度明显高于非作物的分类精度，其原因可能与作物生长周期较短，光谱特征变化明显有关，少耕大豆的分类精度最高，达到99.98%，其余各类作物分类精度均在98%以上。石-钢-塔和建筑-草分类精度较低，这些地物占比较小且训练样本数量较少，光谱特征较为单一，难以提取其空间－光谱特征；对于Pavia Center数据集的各类地物，MSFC算法分类精度均在97%以上，水体和瓦片2种地物占比较大，纯净像元指数较高，因此分类精度较高，分别为98.89%和99.82%，砖路的训练样本占比最少，且位分布于沥青和阴影之间，容易产生混合像元，因此分类精度最低；对于Pavia University数据集的各类地物，MSFC算法相比其他算法取得了更好的分类结果，训练样本数量较多的柏油路、梅朵斯公园、金属板和裸土分类精度均在99%以上，而阴影和沥青的训练样本数量较少，难以充分提取其空间特征，导致分类精度较低。此外，与其他算法相比，MSFC算法在3个数据集上分类用时均为最短。

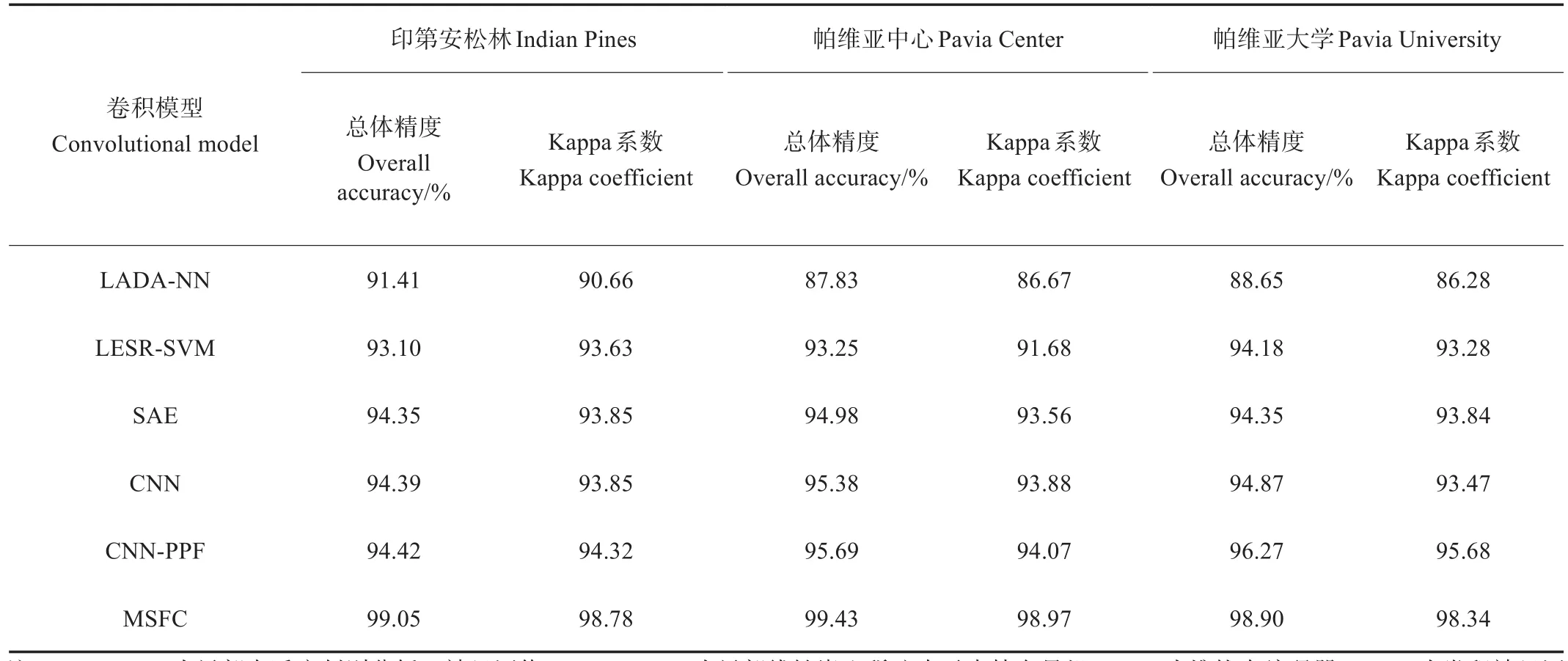
表5 不同算法的总体精度和Kappa系数Table 5 Overall accuracy and Kappa coefficient of different algorithms

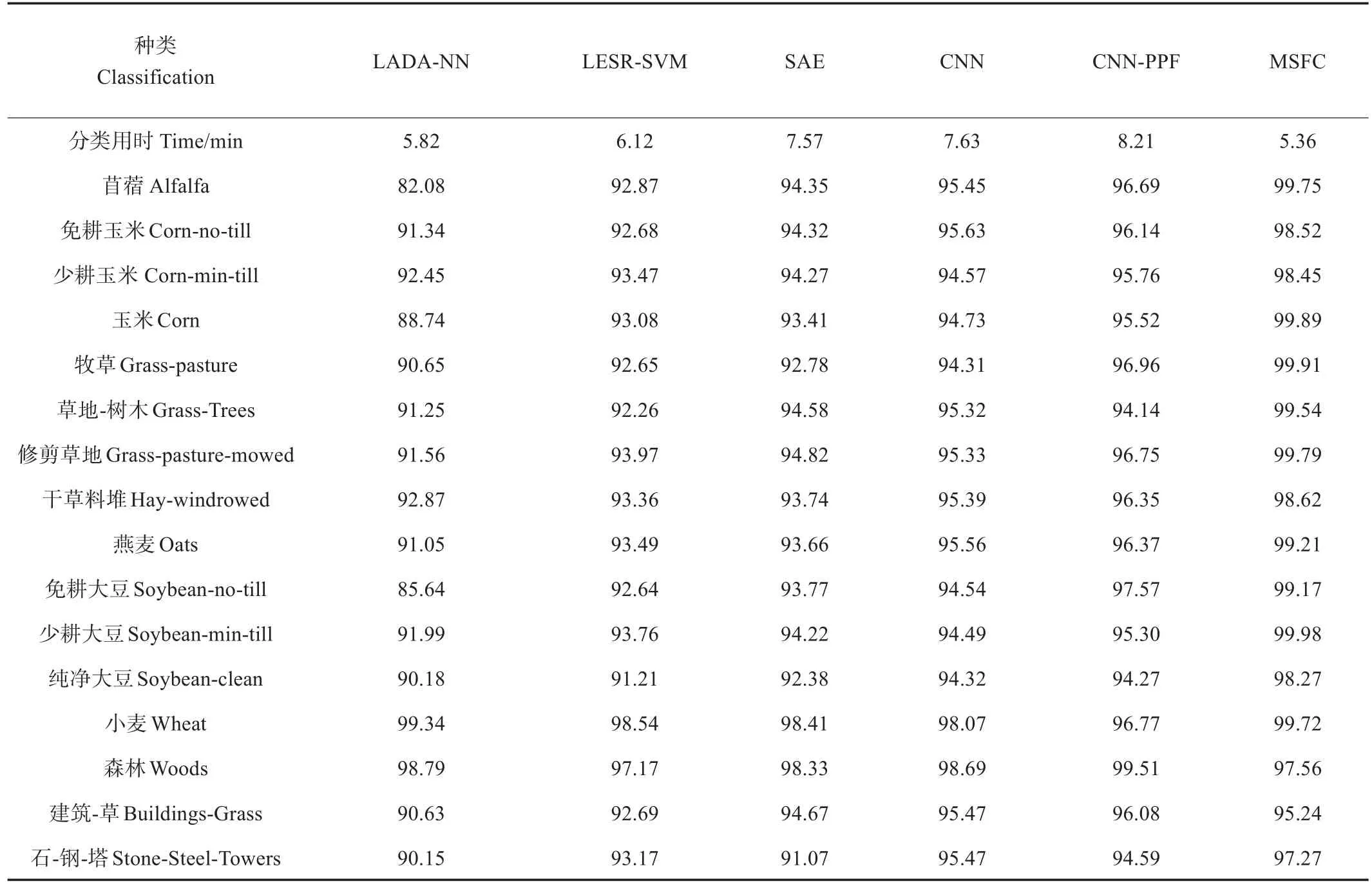
表6 印第安松林数据集分类精度Table 6 Classification accuracy of Indian Pines data set

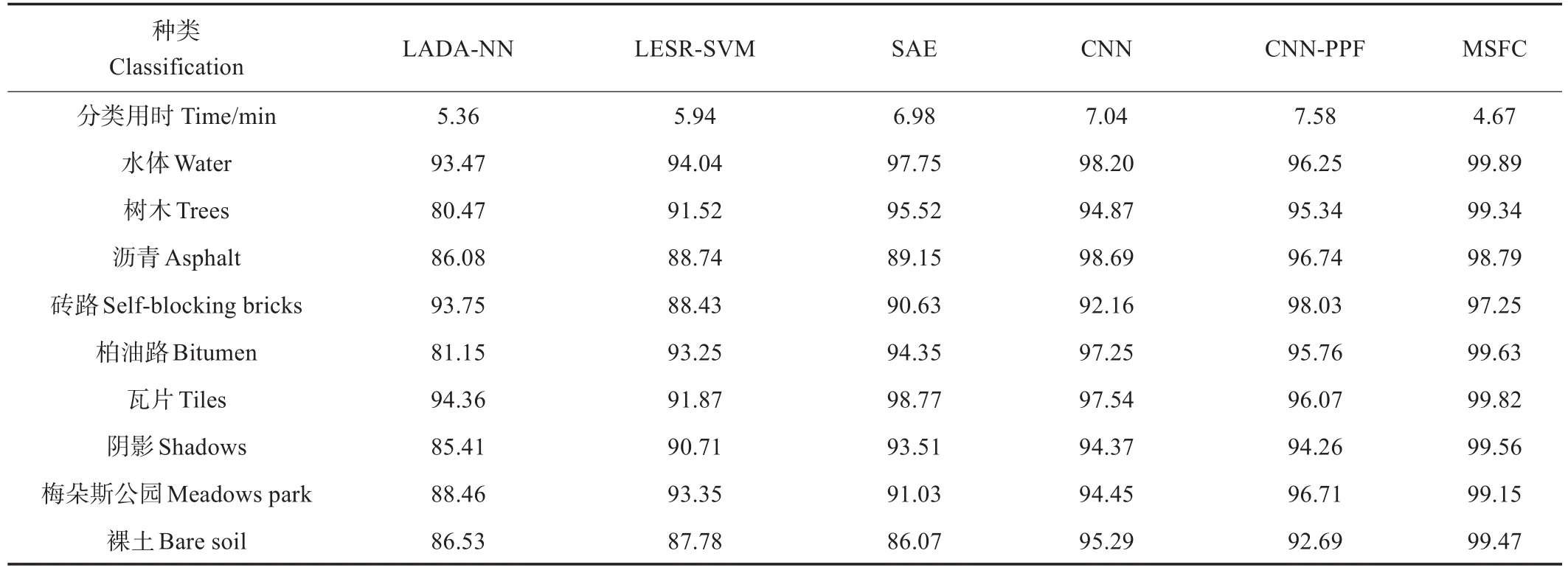
表7 帕维亚中心数据集分类精度Table 7 Classification accuracy of Pavia Center data set

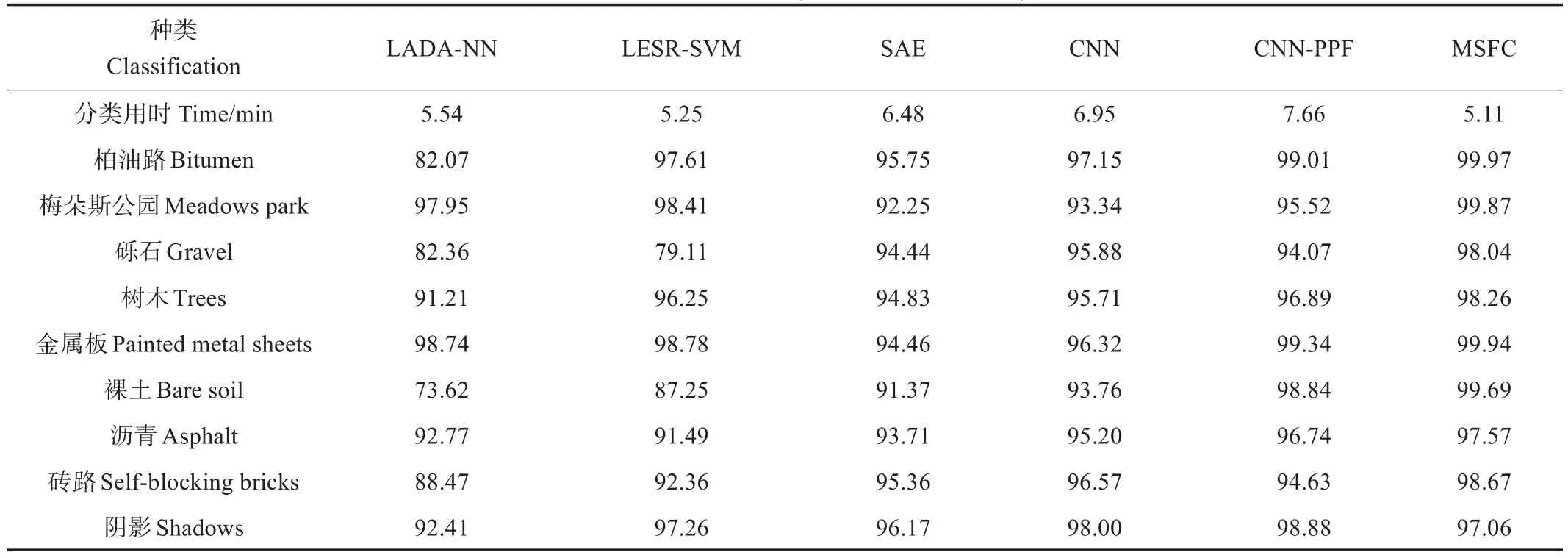
表8 帕维亚大学数据集分类精度Table 8 Classification accuracy of Pavia University data set

各个数据集的分类结果如图7～图9所示。对Indian Pines数据集的分类结果如图7c～7h所示。所有算法对于小麦和少耕大豆表现出较好的分类结果，这2种地物形态学上呈现出规则和聚集的分布形态，能够较好地提取其空间特征，而对于免耕玉米都出现了不同程度的误分现象，其原因可能与交错种植有关。局部自适应判别分析－神经网络（locality adaptive discriminant analysisneural networks，LADA-NN）和CNN-PPF算法对于免耕大豆和玉米误分较为严重，其原因可能是地物样本太少，未能充分提取空间特征，CNN和LADA-NN算法将免耕大豆误分为少耕大豆。对于此类小样本地物，MSFC算法体现出了更好的分类结果，总体精度达到99.05，明显高于其他方法。其他5类方法总体精度分别为91.74%、93.10%、94.35%、94.39%和94.42%；Pavia Center数据集分类结果如图8c～8h所示。对比算法对于瓦片均表现出良好的分类结果，而对于水体则存在不同程度的误分现象，局部自适应判别分析－神经网络（locality adaptive discriminant analysis-neural networks，LADA-NN）、局部线性嵌入稀疏表示支持向量机（locally linear embedding sparse representation-support vector machine，LESR-SVM）和SAE将水面上的波纹误分为瓦片，CNN和CNN-PPF将其误分为沥青，其原因可能与该数据集空间分辨率较高（1.3 m）有关。对于小样本地物同样存在误分现象，局部线性嵌入稀疏表示支持向量机（locally linear embedding sparse representationsupport vector machine，LESR-SVM）和LADA-NN将沥青误分为瓦片，CNN将柏油路错分为砖路，MSFC算法对各类地物均取得了较好的分类结果，总体精度达到99.43%，对于瓦片和水体两类地物取得了极好的分类效果，精度分别为99.82%和99.89%。对比方法的总体精度分别为87.83%、93.25%、94.98%、95.38和95.69%；Pavia University数据集分类结果如图9c～9h所示，对比算法对于裸土和梅朵斯公园均存在较为严重的误分现象，其原因可能是裸土与梅朵斯公园的地表覆盖类型相近，从而表出相似的光谱特征。由于金属板的反射率较高，在空间特征上表现明显，因此各算法均取得了较好的分类结果。MSFC算法对于各类地物均有较好的分类效果，总体精度为98.90%，对比算法的总体精度分别为88.68%、94.18%、94.35%、94.87%和96.27%。

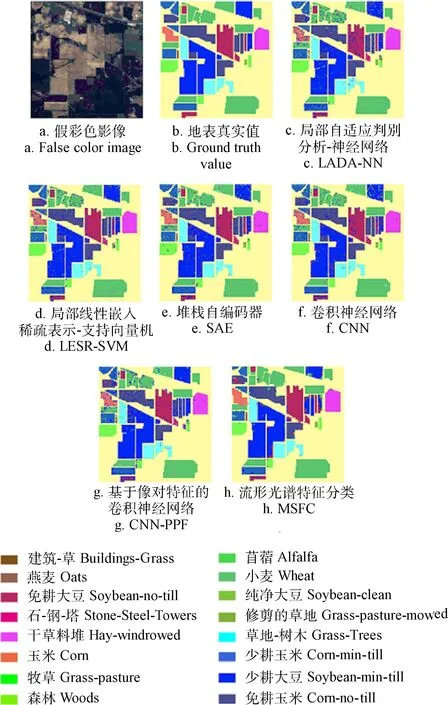
图7 印第安松林数据集分类结果Fig.7 Classification of Indian Pines data set

图8 帕维亚中心数据集分类结果Fig.8 Classification of Pavia Center data set

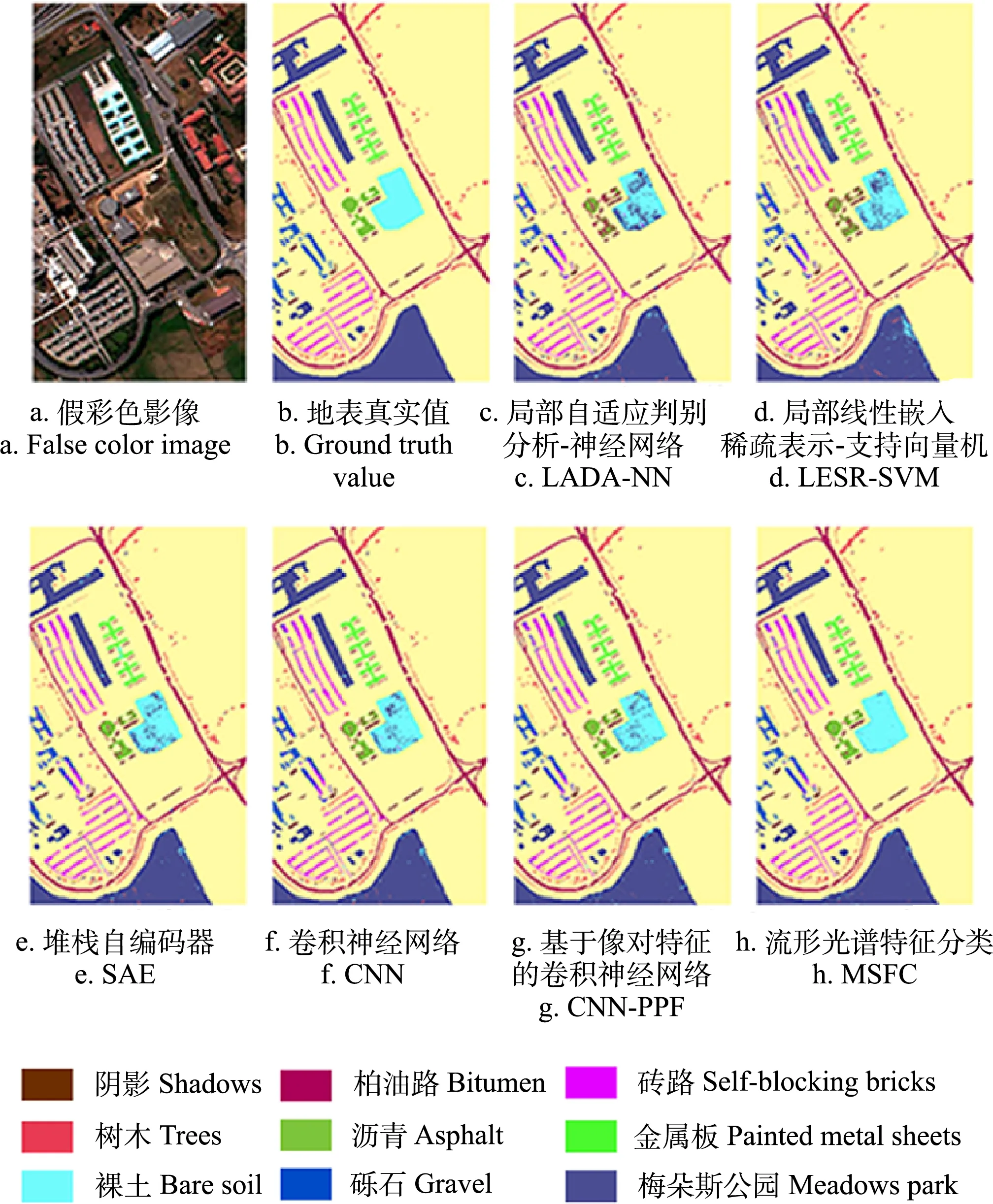
图9 帕维亚大学数据集分类结果Fig.9 Classification of Pavia University data set

3 结 论

本研究融合流形学习和深度学习的方法提出了一种基于流行光谱特征的高光谱影像分类算法（manifold spectral feature based calssification，MSFC），在3个高光谱数据集上进行分类，试验结果表明：

1）降维后的高光谱数据与原始数据相比，分类的用时减少同时总体精度和Kappa系数有所提升，有效解决了高光谱数据存在的波段冗余问题，改善了“休斯（Hughes）”现象，提高了高光谱数据的利用效率。

2）t-SNE算法作为一种非线性流形学习降维算法，能够更好地寻找高光谱数据的低维流形表示，改善了小样本问题。与其他降维算法进行对比，t-SNE算法体现出了显著的类内聚集性和类间可分性，避免了拥挤问题，提高了高光谱影像的分类精度。

3）卷积神经网络具有强大的特征提取能力，能够提取更为深层和抽象的特征，MSFC算法在3个数据集的总体精度分别为99.05%、99.43%和98.90%，与CNN相比分别提升了4.66%、4.05%和4.03%，充分发挥了流形学习降维与卷积神经网络特征提取的优势，为高光谱遥感影像分类研究提供了一种思路。

获取高光谱影像的标记样本数据通常较为困难，下一步研究工作将考虑如何在有限标记样本的条件下构建分类模型，以期获得更好的分类结果。