一类捕食-食饵模型渐近稳定性分析
2020-05-18洪泽澎王治国
洪泽澎,王治国
(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)
0 引 言
恒化器[1-3]是一种用于细菌连续培养的实验装置,它由营养器、培养器和溢出器组成。由于恒化器具有良好的可控可测性,从而在实验室环境中得到广泛应用。恒化器模型的研究一直是生物和数学工作者所关注的热点课题之一[4-5]。文献[6]首次提出单物种的恒化器模型。由于捕食关系在自然界中广泛存在,大量研究致力于讨论捕食关系中的生态动力学行为。Fussmann等[7]研究了一类具有年龄结构的捕食系统的hopf分歧现象,Yoshida等[8]进一步讨论了由食饵进化驱动的生态动力学行为。Frickel等[9]研究了一类捕食食饵双进化的动力学行为。
Butler等[10]在单物种恒化器模型基础上提出了营养物质氮-小球藻-轮虫的食物链恒化器模型:
(1)
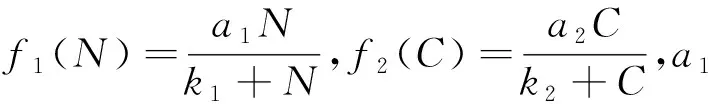
Butler给出了系统(1)平衡点存在的充要条件,分析了在相应平衡点处系统的稳定性。况阳[11]在系统(1)的基础上进一步讨论了系统极限环的存在唯一性及其位置。Bhattacharyya等[12]讨论了引入食饵庇护所情况下的动力学行为。
在上述模型(1)中,假定系统中的氮、小球藻和轮虫拥有相同的稀释率,实际上,轮虫作为生命个体,应该存在死亡率,因此在恒化器模型中考虑轮虫的死亡率更具实际意义,因此本文重点考虑死亡率对恒化器中培养物的影响。假设轮虫的死亡率m>0,结合系统(1),考虑如下的模型:
(2)
当引入死亡率m≠0后,系统(2)不再具有守恒律,从而不能简化方程,这为讨论系统的动力学行为带来了很大的困难。所以本文着重讨论正平衡点处的稳定性,给出了正平衡点渐近稳定的充分条件,从而从理论上为恒化器中物种的培养提供确实可靠的方案。
1 平衡点的稳定性分析
首先研究系统(2)平衡解的存在性,系统的平衡解满足以下方程组:
(3)
显然系统(2)总存在平衡解E0:=(N0,0,0)。

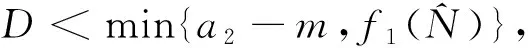
证明 ⅰ)令方程组(3)中B=0,则有
(4)
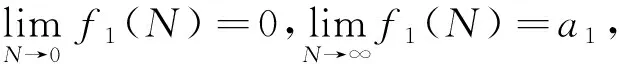

下面分析系统 (2) 的平衡解E0、E1、E2的稳定性。
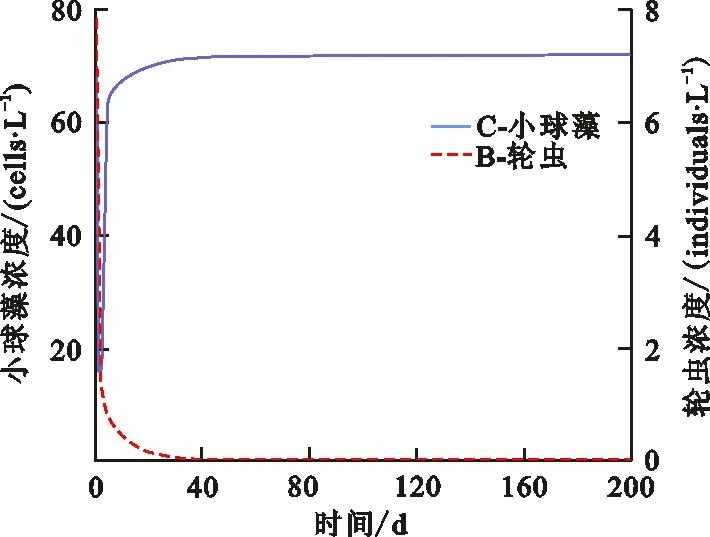
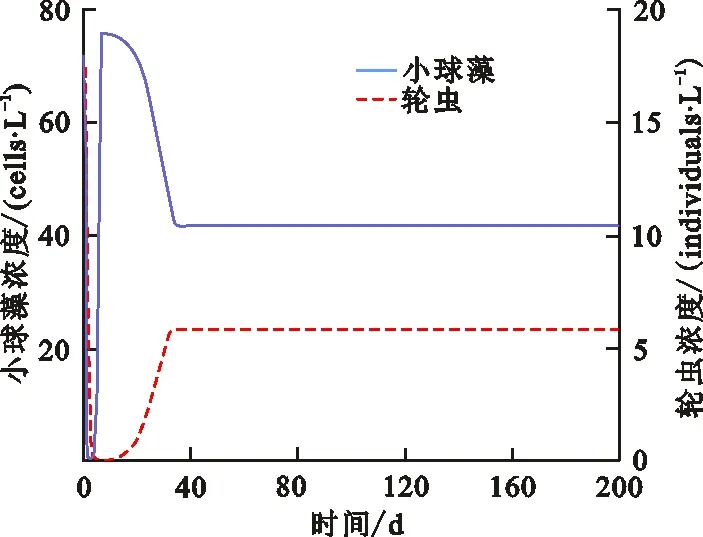
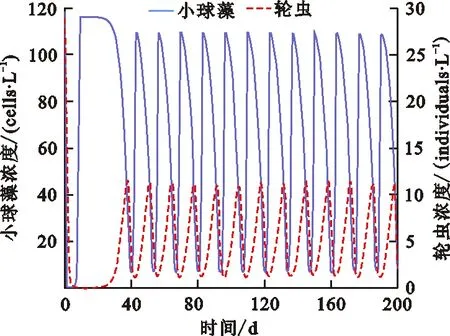
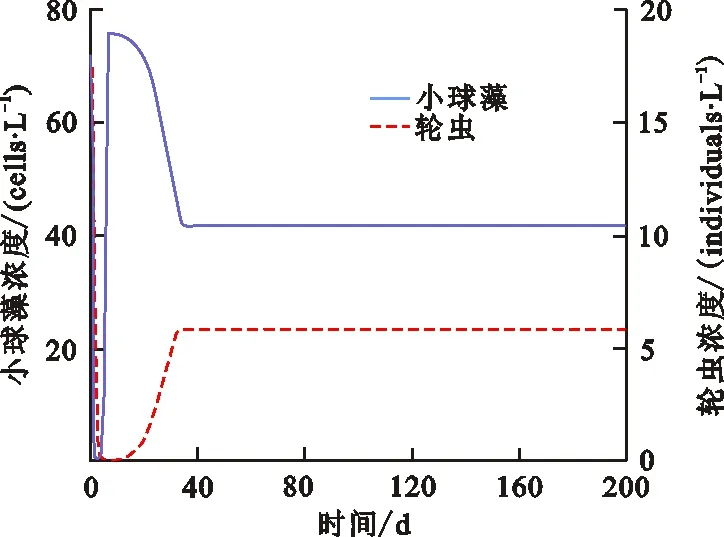
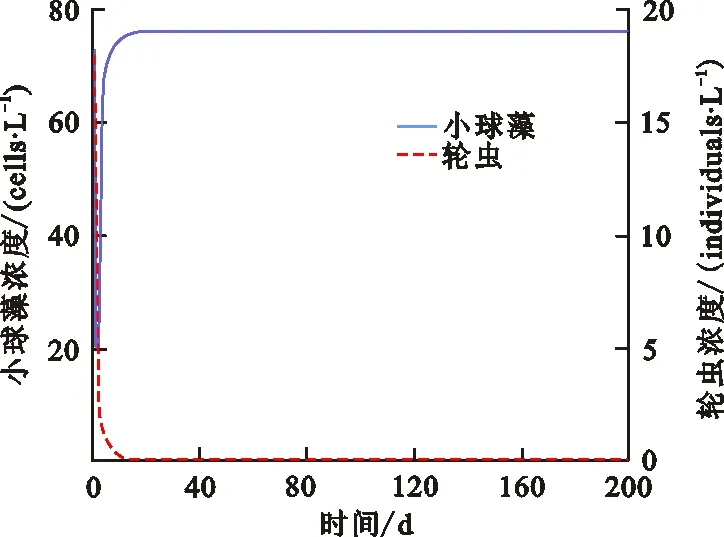
定理2 ⅰ) 如果D>f1(N0), 则E0(N0,0,0) 是局部渐近稳定的, 当D ⅱ)如果f2(C*)-m 证明 系统(2)的Jacobi矩阵为 Q(N,C,B)= 从而系统 (2) 在E0=(N0,0,0) 对应的线性化矩阵为 则Q(E0)对应的特征多项式为 P0(λ)=(λ+D)(λ+D-f1(N0))(λ+D+m) 于是P0(λ)的特征根为λ1=-D<0,λ2=-D-m<0,λ3=f1(N0)-D。所以当D>f1(N0),E0点是局部渐近稳定的,而D 在E1=(N*,C*,0)处对应线性化矩阵为 Q(E1)= 则Q(E1)特征多项式为 C*f'1(N*)f1(N*)] [Π+D+m-f2(C*)] 设P1(Π)的特征根分别为Π1,Π2,Π3。当D 因此,Π1、Π2实部必定小于0。另一方面Π3=f2(C*)-D-m,因此当f2(C*)-m Q(E2)= 则Q(E2)特征多项式为 P2(λ)=λ3+A1λ2+A2λ+A3 其中 A1=M+D+θ A3=(D+θ)(D+m)H 设P2(λ)的特征根分别为λ1,λ2,λ3,根据Hurwitz判别法[13],有 当且仅当H1>0,H2>0,H3>0时,有Reλ1<0,Reλ2<0,Reλ3<0,故E2平衡点局部渐近稳定。显然A3>0,因此H2与H3同号,仅需分析H1,H2的符号。 H1=A1=M+D+θ, H2=A1A2-A3=D2M+DHM+ HMm+M2θ+Mθ2+ 表1 平衡点存在和稳定性分析Tab.1 The existence and stability analysis of steady state 本节研究系统的一致持久性。由于物质浓度的非负性,定义系统(2)的生物可行域为 Y={(N,C,B)|N,C,B≥0} 由定理1知:①平凡解E0=(N0,0,0)总是存在的;②如果D 定义映射T:Y→Y是系统(2)的解映射,即∀D0∈Y,系统(1)的解T(D0)∈Y。令Y0={(N,C,B)∈Y,C≢0,B≢0},∂Y=YY0,则有以下结论。 引理1 如果D (5) 证明 假设式(5)不成立,则存在p0∈Y0,使得 因此∃t1>0,∀δ0>0,使得 ‖N-N0‖<δ0,‖C-0‖<δ0, ‖B-0‖<δ0,∀t>t1 (6) 由函数的连续性知,存在充分小的ε1(δ0)>0,使得 f1(N)>f1(N0)-ε1,∀‖N-N0‖<δ0 (7) ∀‖B‖<δ0 (8) 由系统(2)和不等式(7)~(8)可得 (f1(N0)-2ε1)C-DC>0 (9) (10) 引理2 如果f2(C*)>m且D (11) 证明 假设式(11)不成立,则∃p1∈Y0,使得 因此∃t2>0,∀δ1>0,使得 ‖N-N*‖<δ1,‖C-C*‖<δ1 ‖B-0‖<δ1,∀t>t2 (12) 由函数的连续性,存在充分小的ε2(δ1)>0,使得 f2(C)>f2(C*)-ε2,∀‖C-C*‖<δ1 (13) 由系统(2)和不等式(13)可得 ε2)B-(D+m)B>0 (14) (15) 定理3 如果f2(C*)>m且D (16) 证明 若初始条件p2=(N0,C0,B0)∈Y0, 容易看出解N(t)>0,C(t)>0,B(t)>0, 即T(Y0)⊆Y0。 令M∂={p2∈∂Y0,T(p2)∈∂Y0,∀t≥0}。 ω(P0)是轨道O+(p2)={T(p2):t≥0}的ω-极限集,则有: ω(ψ)={E0}∪{E1},∀ψ∈M∂ 定义连续函数h:Y→[0,+∞)如下: h(φ)=min{φ2,φ3},∀φ∶=(φ1,φ2,φ3)∈Y 易知h是连续的。h-1(0,+∞)⊆Y0,且h满足如果h(ψ)>0或ψ∈Y0,其中h(ψ)=0,那么h(T(ψ))>0,∀t>0。即h是一个关于半流T:Y→Y的广义距离函数。显然,半流T:Y→Y是点耗散的。T:Y→Y是紧的(参考文献[14]定理3.4.8),因此半流T:Y→Y,t≥0存在一个全局吸引子A0。通过引理1与引理2知{Ei}(i=0,1)在Y中是孤立的,且ωs({Ei})∩h-1(0,+∞)=∅。其中ωs({Ei})是{Ei}中的稳定集[15]。此外,显而易见,在∂Y0中{E0}∪{E1}均无法形成一个环。通过文献[15]中定理3,可知存在一个η>0,使得 因此式(14)成立。 本节采用文献[7]中的参数,利用Matlab对系统(2)进行数值模拟,进而讨论系统(2)的动力学行为以及参数对系统(2)解的影响。除特殊说明,其他参数默认取值为:N0=80 μmol·L-1,a1=3.3 d-1,k1=4.3 μmol·L-1,a2=2.25 d-1,k2=15 μmol·L-1,γ=0.25,m=0.055 d-1。 分别选取D=0.001、 1.5、1.6、2.0 d-1,初值N0=80 μmol·L-1,C0=10×109cells·L-1,B0= 5×103individuals·L-1。数值结果表明:在稀释率D很小时,小球藻和轮虫共存(图1(a)所示),随着D增大时,小球藻和轮虫种群呈现周期震荡(图1(b)所示),继续增大D时,小球藻和轮虫又共存于正的平衡解(图1(c)所示),最后,轮虫灭绝(图1(d))。 (a) D=0.001 d-1 (b) D=1.5 d-1 (c) D=1.6 d-1 (d) D=2.0 d-1图 1 稀释率D对系统动力学的影响Fig.1 The effect of the dilution rate D 取D=1.6 d-1,数值结果表明:当死亡率m很小时,轮虫和小球藻可以共存(图2(a)所示),随着m的增大,轮虫逐渐灭绝,生态环境中仅剩下小球藻(图2(b)所示)。 (a) m=0.055 d-1 (b) m=0.55 d-1图 2 死亡率m对系统动力学的影响Fig.2 The effect of the mortality rate m 在D=1.6 d-1的情况下, 分别选取N0=40、80、120、600 μmol·L-1进行数值模拟。数值模拟结果表明当N0很小时,轮虫灭绝(图3(a)所示), 随着N0增大,小球藻和轮虫达到共存(图3(b)所示),进一步增大N0后,小球藻和轮虫种群呈现周期性振荡(图3(c)所示),最后,N0增大到一定程度后, 轮虫再次灭绝(图3(d)所示)。 (a) N0=40 μmol·L-1 (b) N0=80 μmol·L-1 (c) N0=120 μmol·L-1 (d) N0=600 μmol·L-1图 3 初始输入浓度N0对系统的影响Fig.3 The effect of the initial input concentration N0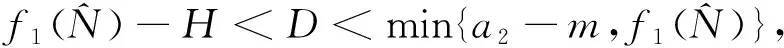
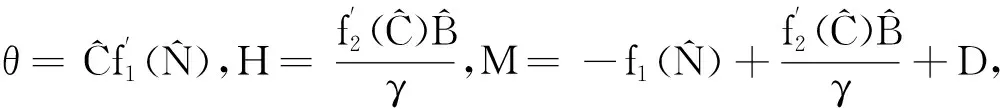
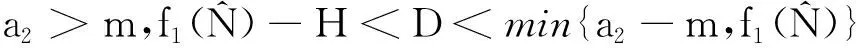
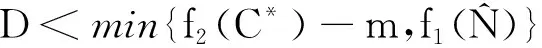

2 系统的一致持久
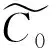
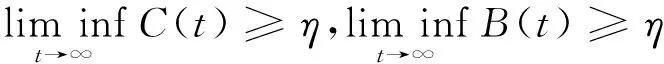
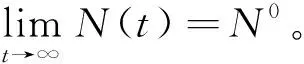
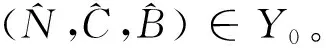
3 数值模拟
3.1 稀释率D对系统(2)的影响
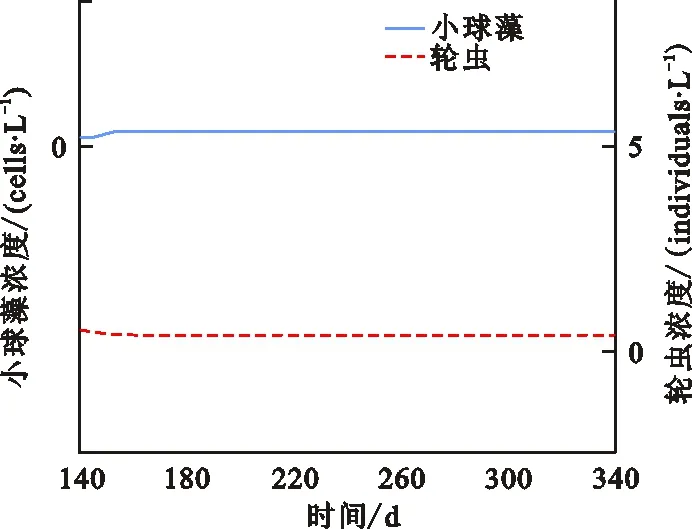

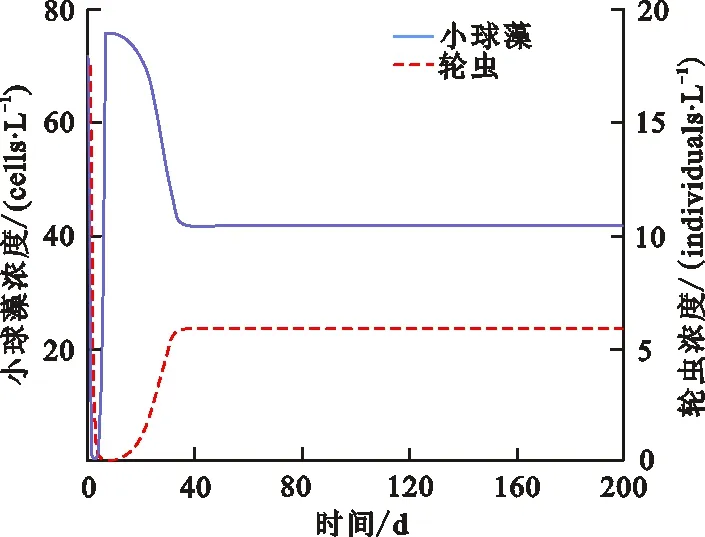

3.2 死亡率m对系统(2)的影响
3.3 初始输入浓度N0对系统(2)的影响