带有临界项的薛定谔-泊松系统的基态解
2020-05-18董思雨冯晓晶
董思雨,冯晓晶
(山西大学 数学科学学院, 山西 太原 030006)
1 引言及主要结论
薛定谔-泊松系统作为描述带电粒子和电磁场相互作用的孤波模型, 在量子力学和半导体理论中应用广泛[1-3]。文献[1-2]研究了薛定谔-麦克斯韦方程, 文献[3]研究了模拟电磁波在等离子体中传播的薛定谔方程。 近年来, 许多数学家研究了如下薛定谔-泊松系统
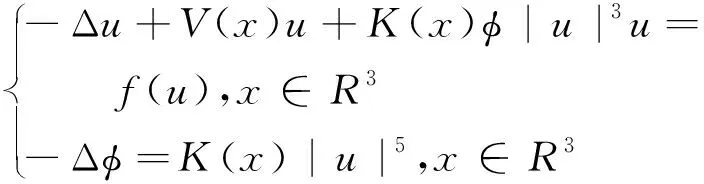
(1)
解的存在性和多重性, 其中V、K、f是连续函数。此后,学者们对系统(1)在V、K、f的不同假设下展开深入研究[4-7]。 当f是周期渐近线性函数且满足单调性条件,文献[4]运用Nehari流形方法获得系统(1)基态解的存在性, 且当f具奇性时, 得到了系统(1)无穷多几何不同解的存在性。文献[5]讨论了V为径向函数且f满足超线性增长条件时, 系统(1)存在无穷多解。当V(x)≡1,f(t)=|t|p-1t(1 近几年, 临界薛定谔-泊松系统相关研究备受关注。带有临界非线性项的薛定谔-泊松系统得到广泛研究[7-10]。文献[8]研究了系统 (2) 基态解的存在性, 在V,K的特定假设下,利用变分方法证明了式(2)至少存在一个正的基态解。 在f(x,u)=λf(x)u+|u|4u时, 文献[9]通过变分方法得到式(2)至少存在一个基态变号解且证明了其能量是基态解能量的2倍。 在f(x,u)=u5时,文献[10]利用环绕引理研究了高能量解的存在性。 带有临界非局部项的薛定谔-泊松系统也得到广泛研究[11-12]。文献[11]研究了如下带有非局部项的薛定谔-泊松系统 (3) 通过运用山路定理和集中紧性原理得到了系统(4)正解的存在性。 设E:={h∈L∞(R3):|{x∈R3:|h(x)|≥ε}|<∞,∀ε>0}。 本文研究如下带有双临界项的薛定谔-泊松系统 (4) 基态解的存在性, 其中V∈C(R3)和f∈C(R3×R,R)是渐近周期函数。假设: H2) ∃Vp∈L∞(R3), 关于xi(i=1,2,3)是1-周期的, 使得对于一致的x∈R3, 有V-Vp∈E, 且V(x)≤Vp(x)。 S1) ∃q∈(4,6), 使得∀(x,t)∈R3×R, 有|f(x,t)|≤C(1+|t|q-1),其中C>0。 S6)fp∈C(R3×R,R), 关于xi(i=1,2,3)是1-周期的, 使得∀(x,t)∈R3×R, 有 ⅰ) |fp(x,t)|≤|f(x,t)|; ⅱ) |fp(x,t)|-|f(x,t)|≤|h(x)|(|t|+|t|q-1),h∈E; ⅳ) ∀(x,t)∈R3×R, 都有fp(x,t)t≥0。 主要定理如下: 定理1 假设H1)~H2)及S1)~S6)成立, 系统(4)至少存在一个基态解。 设 命题1[12]下列性质成立: (5) 容易验证系统(4)的弱解是下面能量泛函的临界点。 为了证明主要结果,首先给出以下引理。 证明 (ⅰ) 当t>0, 令g(t):=I(tu), 又g′(t)=〈I′(tu),u〉=0⟺tu∈N。 ⅲ) 根据S1)和S2), ∀ε>0, ∃Cε>0, 使得对一切(x,t)∈R3×R, 有 (6) 由ⅰ)知, 当u∈S1, ∃tu>0, 使得tuu∈N。 故当ε>0足够小时, 由式(6)得 M|u|μ-L|u|2≤F(x,u) (7) 因此, 又由S3), 有 得出矛盾。 因而∃Cw>0,使得tu≤Cw。 ⅲ) 当ρ>0充分小时, ∀u∈Sρ, 有 显然,∀u∈N, ∃t1>0, 使得t1u∈Sρ。 因此由引理1中ⅰ)得 (8) 引理2I在N上强制。 证明 即当u∈N且‖u‖→∞, 有I(u)→∞。 定义uε(x)=η(x)Uε(x), 当ε→0+, 有 (9) (10) 其中Ks(2≤s<6)是正常数。 从而根据引理4和式(10), 当ε>0足够小时,有 引理7[16]ⅰ) 若{wn}是Ψ的1个 (PS) 序列, 则 {m(wn)} 是I的1个 (PS)序列。 若 {un} 是I的1个(PS)序列, 则 {m-1(un)} 是Ψ的1个 (PS) 序列。 ⅲ) 在N上I的极小值点是系统(4)的基态解。 定理1的证明 根据引理7中ⅲ), 只需证c即可。 若u≠0,则u∈N且c≤I(u).根据范数的弱下半连续,Fatou引理及S3)可得 即I(u)=c。即证。 若u=0,由集中紧性原理[18]得知只有如下2种情况: ⅱ) 非消失, 即∃R>0, 使得 (11) 如果情况(ⅰ)出现, 根据文献[19]中的引理3.8, 在Ls(R3)(2 (12) 则有 (13) 下证Ip(v)=c。先证Ip(v)≤c。事实上,根据{un}的有界性和引理8有 因此有 综上, 由引理7的ⅲ)得系统(4)基态解的存在性。 应用集中紧性原理和Nehari流形的方法获得系统基态解的存在性。由于系统含有位势函数和非线性项, 需通过应用周期函数逼近和增长性条件的方法获得临界值的存在性;由于系统具有双临界项, 缺乏紧性, 需应用集中紧性原理获得基态解的存在性。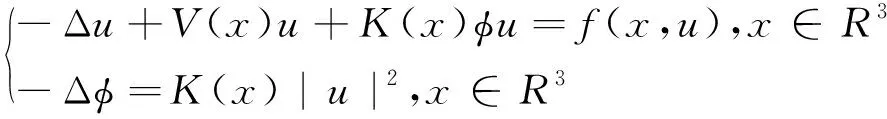
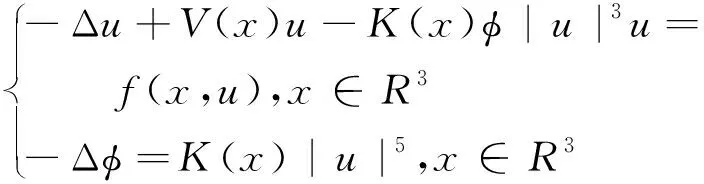
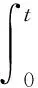
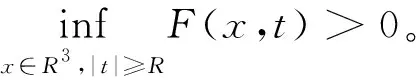
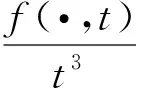
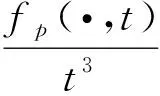
2 预备知识
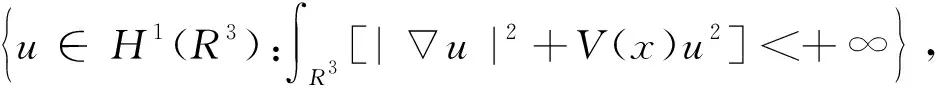
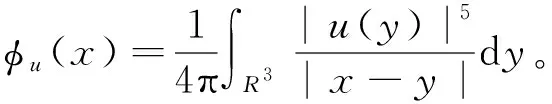
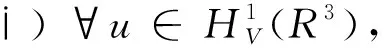
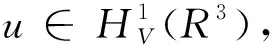

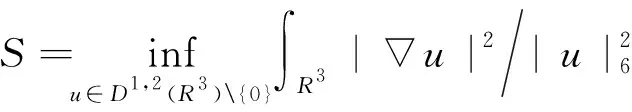
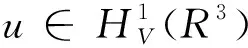
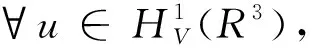
3 定理的证明
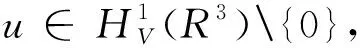
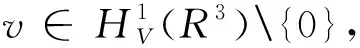
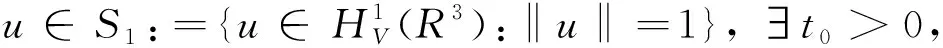
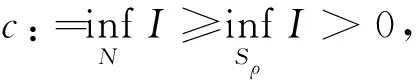
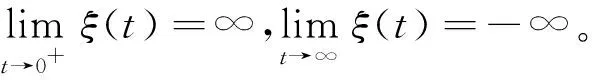
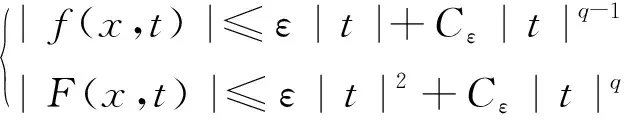
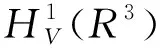
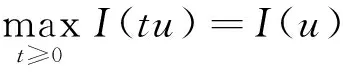
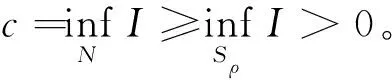
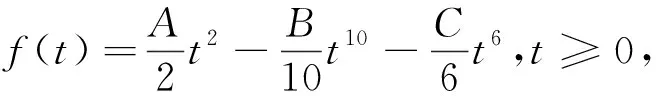
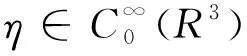
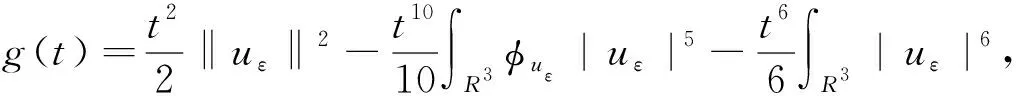
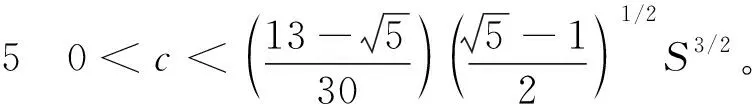
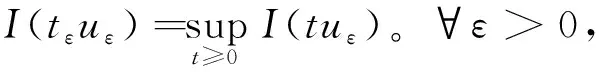
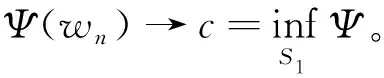

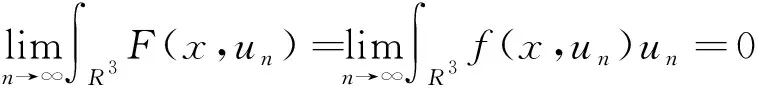
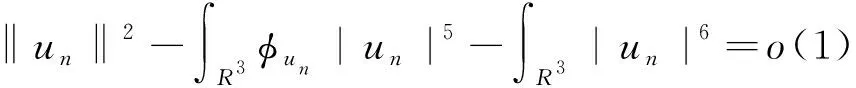

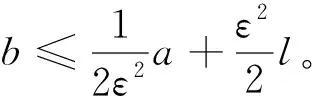

4 结 语
