环境温度对微小型弹簧抗力的影响

朱文凯，王雨时，邹陈来，闻 泉，王光宇

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

弹簧是引信中常见的一种抗力件，在引信中应用比较广泛的弹簧有圆柱形螺旋压缩弹簧、扭转弹簧、圆台形螺旋压缩弹簧和鼓形螺旋压缩弹簧等。引信弹簧材料一般选用特殊用途碳素弹簧钢丝(GJB1497-1992)，此种钢丝采用T9A、T10A工具钢冷拉制成。钢丝直径为0.2～1.5 mm[1]。引信工作环境复杂，一般工作环境温度在-40～50 ℃内。弹簧是引信重要抗力件，其抗力散布对性能影响非常重要，已有文献在这方面做了很多研究。文献[2]提出一种新的工艺流程：缠绕成型→回火→电镀→强压处理，按此工艺流程加工的引信弹簧性能良好。文献[3]研究了镀层对微小型弹簧抗力的影响。文献[4]则论述了制造误差对于弹簧抗力的影响。

弹簧抗力主要与弹簧材料弹性模量[5]和弹簧钢丝直径[6]有关。文献[7]试验表明钢随着温度升高其弹性模量数值减小。但目前尚未见有文献揭示环境温度与弹簧抗力之间的变化关系。

1 理论推导

1.1 常温下引信弹簧抗力的计算

引信弹簧抗力公式[8]:

(1)

式(1)中，n为弹簧的有效圈数，D为弹簧中径，d为弹簧钢丝直径，G为弹簧钢丝材料的切变模量，λ为弹簧变形量，λ=H-hc，H为弹簧自由高度，hc为弹簧工作(检验)高度。

1.2 温度变化对弹簧的影响

1.2.1弹簧尺寸受温度影响的变化

文献[9]和文献[10]给出了金属材料一维热变形计算公式为:

(2)

式(2)中，lx为环境温度中金属材料长度，l0为常温中金属材料长度，α为材料热膨胀系数，T为环境温度，T0为常温(20 ℃)。

当弹簧处于受压状态时，温度变化主要影响弹簧钢丝直径和长度。弹簧钢丝直径的变化直接影响弹簧抗力。文献[11]和文献[12]均指出了金属材料的热膨胀系数是各向同性的，即弹簧钢丝直径热变形计算公式为：

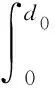
(3)

式(3)中，dx为环境温度中弹簧钢丝直径，d0为常温中弹簧钢丝直径。

长度的变化主要影响弹簧中径和弹簧自由高度。为了找出弹簧钢丝长度与弹簧中径、弹簧自由高度间的关系，将单圈弹簧钢丝沿螺旋方向拉直展开如图1所示。

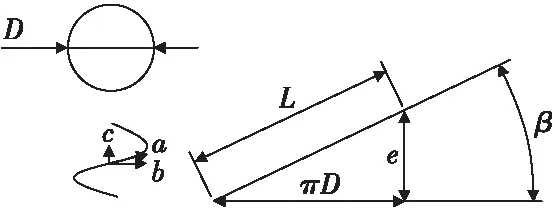
图1 单圈弹簧展开示意图 Fig.1 Diagramof lap spring expansion

由图1可看出，弹簧钢丝受环境温度影响沿螺旋方向a的伸缩量可以分解为螺旋圆的切线方向b和竖直方向c，这两个方向弹簧伸缩量分别导致了弹簧自由高度和弹簧中径的变化，而弹簧的螺旋角β并未发生变化。弹簧钢丝长度L与弹簧中径D和弹簧节距e满足以下关系:

(4)

结合式(2)可给出环境温度变化引起弹簧中径和节距变化的计算公式：

(5)

式(5)中，n为弹簧总圈数，Lx为环境温度中弹簧钢丝长度，L0为常温中弹簧钢丝长度，Dx为环境温度中弹簧中径，D0为常温中弹簧中径，ex为环境温度中弹簧节距，e0为常温中弹簧节距。

化简得：

(6)

式(6)中，ΔT=T-T0。

弹簧自由高度的计算公式为[1]：

H=n0e+xd

(7)

式(7)中，n0为弹簧有效圈数，x为弹簧支撑圈数，其数值与弹簧两端处理情况有关，一般取1.5，2，2.5，常用的是2。

结合式(3)和式(6)可给出环境温度变化引起弹簧自由高度变化的计算公式：

Hx=(1+αΔT)H0

(8)

式(8)中，Hx为环境温度中弹簧自由高度，H0为常温中弹簧自由高度。

弹簧工作高度hc为固定值，在室温下弹簧变形量计算公式为：

λ0=H0-hc

(9)

结合式(8)和式(9)进而可推出环境温度变化引起弹簧变形量变化的计算公式：

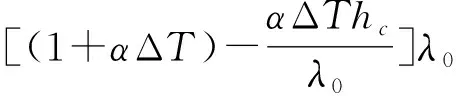
(10)

式(10)中，λx为环境温度中弹簧变形量，λ0为常温中弹簧变形量。

1.2.2弹簧材料切变模量的变化

几乎所有金属(包括合金)的弹性模量都随温度而变化。文献[13]给出了金属材料的弹性模量随温度变化的一般规律：

Ex=E0(1-25αΔT)

(11)

式(11)中，Ex为环境温度中金属材料的弹性模量，E0为常温中金属材料的弹性模量。

文献[14]给出了弹性模量E与切变模量G的关系:

(12)

式(12)中，ν为泊松比。

1.3 环境温度下弹簧抗力的计算

在相同检验高度hc下，环境温度下引信弹簧抗力公式为：

(13)

联立公式(3)、(6)、(10)、(11)和(12)可解出：

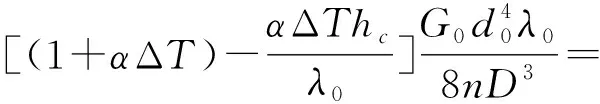
(14)

式(14)中，Gx为环境温度中金属材料的切变模量，G0为常温中金属材料的切变模量，Rx为引信弹簧在环境温度中的弹簧抗力，R0为引信弹簧在常温中的弹簧抗力。

设δ为引信弹簧的平均抗力变化率(环境温度每变化1 ℃，引信弹簧的抗力变化率)。

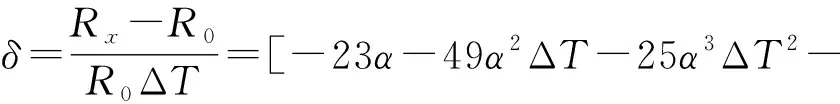
(15)

从式(15)中可以看出：在环境温度发生改变时，弹簧抗力平均变化率的大小主要与材料的热膨胀系数有关，材料热膨胀系数越小，弹簧抗力平均变化率越小。

从数值上可以看出α2和α3的数量级远远小于1，与其相关的各项可以忽略不计，因而有式(15)的近似处理。表1给出了几种引信常用弹簧材料热膨胀系数,可以看出弹簧钢制成的弹簧抗力受温度影响较小。

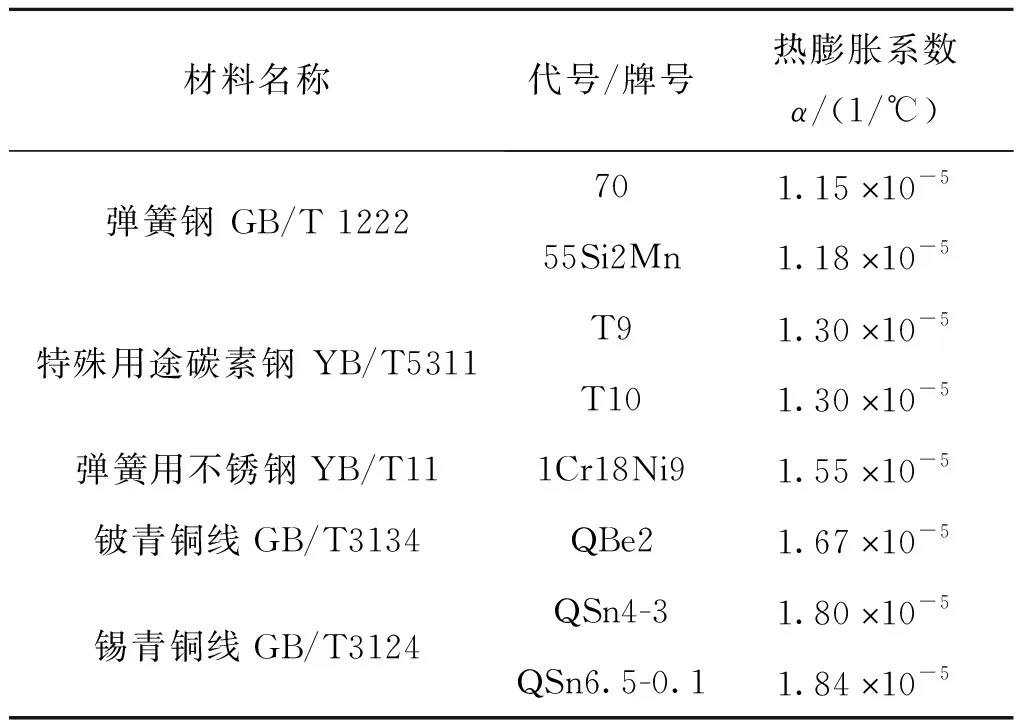
表1 引信常用弹簧材料热膨胀系数[15-16]

2 具体算例及分析

2.1 温度对于弹簧抗力的影响

某引信后坐簧其材料为特殊用途碳素弹簧钢丝，主要结构参数见表2。

表2 后坐簧主要参数

由表2中参数通过式(3)、(11)和(12)计算出不同环境温度中弹簧钢丝直径大小与弹簧材料切变模量大小，带入式(13)，可得工作高度hc=4 mm时，在不同环境温度中抗力变化和抗力平均变化率，见表3。

由表3得后坐簧的抗力随着温度升高而减小；在工作高度hc=4 mm下，后坐簧在不同环境温度中的平均抗力变化率约为0.315‰/℃。

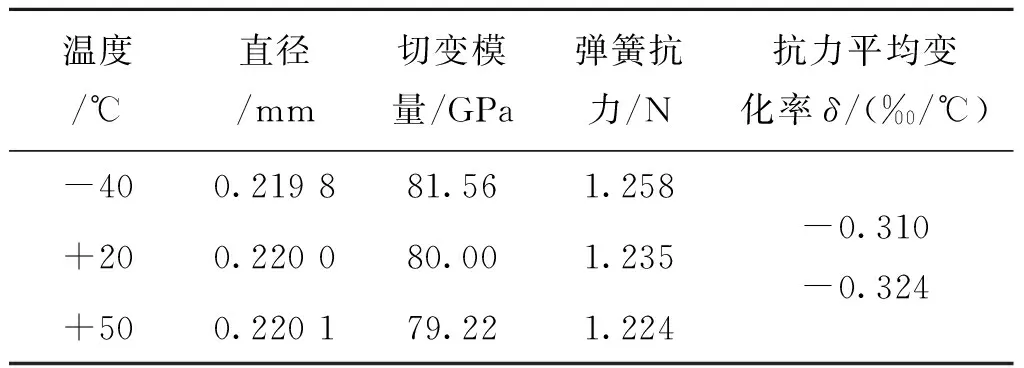
表3 弹簧钢丝受环境温度影响的变化

3 有限元计算

为了与理论推导结果作对比，用仿真软件solidworks建立引信弹簧的三维模型，导入仿真软件ansys中进行热力耦合分析，得出不同环境温度对于弹簧抗力的影响。

图2为引信弹簧的三维模型，图3为不同环境温度下弹簧总变形量分析云图，其具体数据见表4。

图2 后坐簧三维模型Fig.2 Three dimensional model of recoil spring

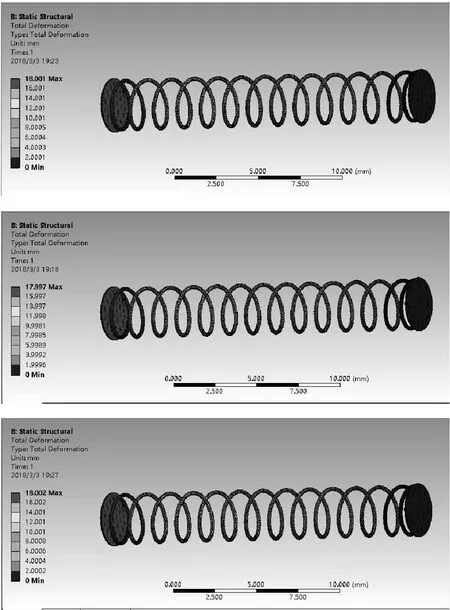
图3 不同环境温度中弹簧总变形量分析云图Fig.3 Total deformation of spring at different ambient temperatures

表4 不同环境温度中弹簧总变形量

Tab.4 Total deformation of spring wire in different ambient temperatures

温度/℃弹簧抗力/N弹簧总变形量/mm-401.24518.001+201.22217.997+501.21118.002

由表4可得后坐簧在不同环境温度中达到相同检验高度时弹簧受到的抗力不同，在工作高度hc=4 mm下，后坐簧在不同环境温度中的抗力变化率0.312‰/℃，与理论推导结果基本一致。

4 试验结果分析

为了与上述理论推导和仿真结果进行对比，测量一组与仿真模型材料相同，结构不同的引信弹簧在相同检验高度下不同环境温度中的抗力值，记录并进行分析。

取100发引信弹簧，分别将弹簧和温度计置于高温和低温两种测试温度中。待温度计示数稳定后，再经过两个小时，开始取下弹簧放于测量工装上，压入预置长度的弹簧测力计和顶杆之间，记下温度计示数和测力计读数。处理后的记录数据见表5。

试验结果表明，引信弹簧抗力在-12.2～+32.4 ℃之间的平均变化率为0.399‰/℃。该数值与理论推导和仿真分析得到的结果基本一致，这也说明了单位温度下的弹簧抗力相对变化量主要受弹簧材料影响，与结构尺寸无关。

表5 不同环境温度中引信弹簧平均抗力

5 结论

本文利用理论推导和有限元分析仿真两种方法分析了引信用圆柱形螺旋压缩弹簧在不同环境温度下抗力的变化情况，两种分析方法结论基本一致，并通过试验验证了所得结论的可信性。结果表明：对于同一种材料的圆柱形螺旋压缩弹簧在不同环境温度中，弹簧抗力随着环境温度升高而减小，这一规律同样适用于其他形状的引信弹簧，但从数值上分析抗力总体变化较小，在引信工程应用中可不予考虑；对于不同材料的引信弹簧在不同环境温度中，弹簧抗力平均变化率的大小与弹簧材料的热膨胀系数有关，弹簧钢材料制成的引信弹簧抗力平均变化率较小，青铜材料的平均变化率略大，不锈钢在两者之间，因此在设计精度较高的引信时可优先选用弹簧钢作为弹簧材料。该结果也说明了弹簧抗力通常不会是引信在恶劣环境温度中瞎火的原因。