磁异常信号奇异值分解的随机共振检测方法

李启飞，吴 芳，韩蕾蕾，范赵鹏，李沛宗

(1.海军航空大学，山东 烟台 264001；2.解放军91550部队，辽宁 大连 116000；3.解放军91001部队，北京 100000)

0 引言

磁异常探测作为水下目标探测的有效手段，已被广泛应用于军事领域。军事领域主要使用航空器作为载体，搭载磁探测平台，对所在空域进行磁场探测。当水下存在目标时，目标会造成附近磁场的异常波动。对该异常波动信号进行处理，从而实现对水下目标的检测，是本文的研究内容。磁异常探测领域研究主要分为两个部分：一是水下目标磁场模型的建立，主要方法包括边界积分法[1-2]、磁偶极子法[3]、有限元法[4]、积分方程法[1, 5]等；二是磁异常信号的处理，侧重于对水下目标磁场信号的检测，目前主流方法包括信号的时域特征分析、频谱分析、时频特性分析[6]、基于标准正交基函数[7](Orthonormalized Basis Function，OBF)分解、熵滤波器检测[8]等。

在实际检测过程中，传感器采样信号过低的信噪比，使得目标信号淹没在背景噪声中，从时域上进行分析，很难直接对微弱的磁异常信号进行检测。OBF算法只有在目标信号和噪声合适的情况下才能够使用，熵滤波器对于低信噪比检测能力较差。为了提高对水下目标磁异常信号的检测能力，本文针对上述问题，提出了磁异常信号奇异值分解的随机共振检测方法。

1 探测原理及结果

1.1 水下目标磁场仿真

通过等效磁源对潜艇磁场的分布进行模拟的方法叫做等效磁源法，主要的等效磁体模型有单个磁偶极子模型、旋转椭球体模型和磁偶极子阵列模型等方法。文献[9]中指出，在2.5倍物体长度以上的空间，完全可以把磁性物体视做磁偶极子处理，满足一般工程应用的需求。潜艇一般与反潜机距离百米以上，磁偶极子模型作为等效磁源对潜艇磁场进行仿真，是完全可行的。

在航空磁探反潜过程中，潜艇作为铁磁性目标，其磁场H可以表示为：

(1)

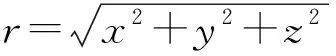
(2)

通过计算，可以得到：

(3)

式(3)中，H为等效磁偶极子磁场强度，Hx,Hy,Hz是磁场强度的三分量，H=ixHx+iyHy+izHz，ix、iy、iz为坐标系中的单位向量。

1.2 奇异值分解原理

在工程应用中，由于噪声的严重干扰，目标信号往往淹没在随机的噪声中，并且噪声与目标信号的频域相互重叠，导致传统的算法难以对低信噪比的信号进行检测。奇异值分解在信号处理领域有着独特的作用，该方法具有理想的去相关特性[10]，能够在强噪声背景下提取有用信号和特征信息[11-12]。

奇异值分解是一种非线性滤波，该方法将时间序列从矩阵角度出发，将时间序列矩阵分解到一些列奇异值对应的时频子空间中，从而对信号进行了提取。

步骤1 将输入信号X构造成Hankel矩阵A，对矩阵A进行奇异值分解，并提取信号Xi。

将时间序列X=[x(1),x(2),…,x(N)]构造成Hankel矩阵A：

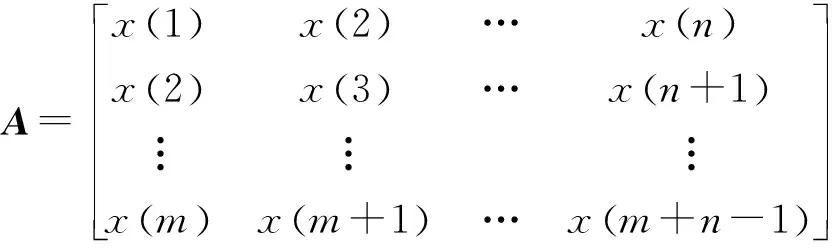
(4)

其中，N=m+n-1。

将Hankel矩阵A进行奇异值分解，并表达成以下形式：

(5)

式(5)中，Σ=diag(σ1,σ2,…,σn)，σi为矩阵A的奇异值，即Σ为奇异值σi降序排序。矩阵A就可以构造为一系列奇异值σi与子矩阵Ai乘积之和，并且子矩阵Ai的形式如下：

(6)

取矩阵Ai的第一行全部元素Xi(t),t=1,2,…，n和最后一列的后m-1个元素Xi(t),t=n+1,…,m+n-1且N=m+n-1，将其组合成新的时间序列Xi：

Xi=[xi(1),xi(2),…,xi(N)]

(7)

奇异值分解所得子信号Xi为原始信号X的线性变换，所以当输入信号为不存在目标磁异常信号时，输出信号Xi仍是高斯白噪声。

步骤2 对Xi进行FFT，并找出在特征频段能量最大的分解信号F[Xi]。

奇异值分解的目的就是寻找在水下信号特征频段处能量最大的奇异值分解信号F[Xi]，该子信号Xi即为最优子信号。取分解阶次n，不同阶次n所对应奇异值σi的大小，σi的分布呈现明显的阶梯形，表明噪声与信号分离情况较好[11]。如式(8)所示，对各奇异值σi下的分解信号Xi在特征频段的能量Ei进行计算，积分区间为[0,1]是因为目标磁异常信号的能量主要集中在0～1 Hz。

(8)

子信号Xi特定频段能量Ei最大时的子信号，即为最优子信号Xi。

1.3 随机共振原理

随机共振是1981年Benzi研究古冰川气象问题时提出的概念，并在生物、电子、信号处理、故障检测[13]方面得到了发展[14-15]。随机共振是指在非线性系统的作用下，噪声会在一定程度上加强系统的输出响应。

经典的随机共振模型可用如下的非线性郎之万方程[16](Langevin Equation)表示：

(9)

其中，V(x)为势函数，表示如下：

(10)

式(10)中，a,b为随机共振系统的结构参数，x为系统的输出，S+Γ随机共振系统的输入信号，S+Γ为水下目标磁场信号，Γ为零均值高斯白噪声。

但当磁异常信号出现时，随机共振系统的输出会出现波动，从而使输出x的标准差(The Standard Deviation，STD)出现异常。因此，可以先依次在随机共振系统的输出信号x中截取一段长度为N时间序列，随后用其输出x的标准差作为检测统计量Y。

对于非线性郎之万方程，可以通过龙格库塔法[17](Runge-Kutta Methods)进行求解：

(11)

式(11)中，τ是采样间隔时间，u(n)是S+Γ奇异值分解后得到的时间序列，xi(n)是随机共振系统的输出。

检验统计量Y表示式如下：

(12)

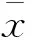
2 奇异值分解-随机共振(SVD-RS)算法

如图1所示，本文对信号的处理一共有两个模块：一是奇异值分解(SVD)模块；二是随机共振(RS)模块。信号通过SVD模块，提取特征频段能量最大信号，随后将其通过随机共振模块，并用统计量Y作为SVD-RS检测器的检验统计量。

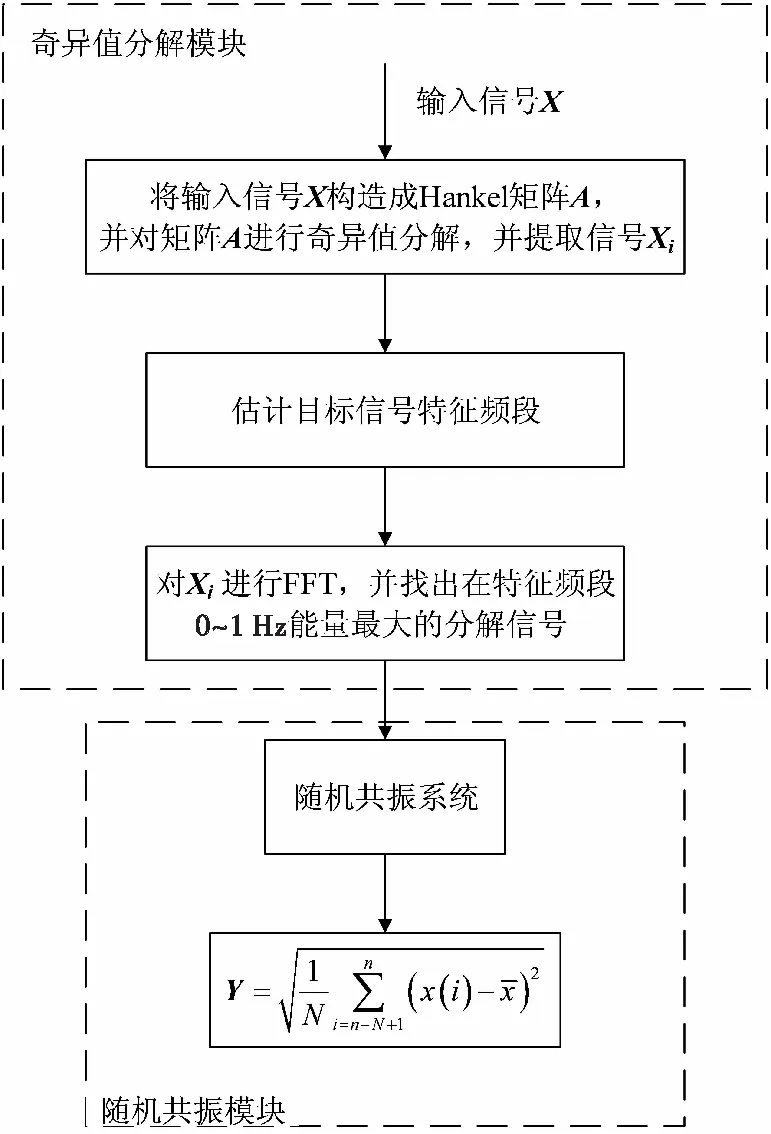
图1 检测流程图Fig.1 Test flow chart of SVD-RS system

根据潜艇磁场产生机理，将潜艇磁矩分为纵向、横向、垂向3个固定磁矩和纵向、横向、垂向3个感应磁矩共6个磁矩，分别记为mil，mit，miv，mpl，mpt，mpv。在一次探测过程中，一般不考虑地磁场变化，那么miv也可以认为不变，因此考虑垂向磁矩mv时不分开考虑。

在仿真情况下，水下目标的磁矩各分量取mil=5×104A·m2，mit=0.27mil，mpl=1.5mil，mpt=0.18mil，mv=0.85mil，磁矩信息来源于文献[18]。默认飞机与目标的高度差为300 m，反潜机航速默认为100 m/s，磁力计采样频率设为100 Hz。随机共振系统的参数a=1,b=70，检验统计量Y的序列窗口长度为N=300。

通过磁偶极子模型仿真水下目标信号，并叠加噪声，图2是输入信噪比SNRin=-3.29 dB时，输入总场信号和目标磁异常信号的时域图和频域图。其中输入信噪比SNRin定义为在磁异常信号出现的时间段(4～6 s)的输入信号的信噪比。

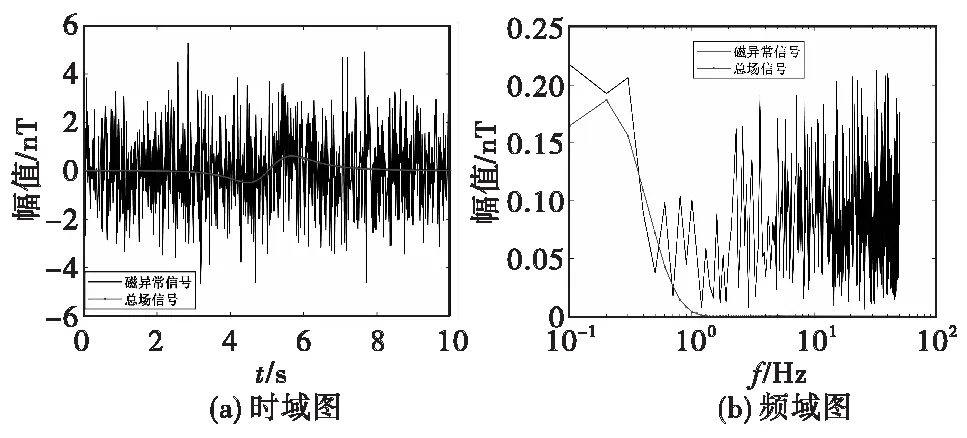
图2 时域图和频域图Fig.2 The time-domain and frequency-domain diagrams

由图3(a)可知，一阶奇异值σ1在信号X中所占权重最大，且由图3(b)可知，一阶分解信号X在特征频段上的能量E1最强，故将提取X1作为输入信号X在奇异值分解系统的输出信号。图3(c)是信号X1的时域图，输入信号X在奇异值分解后所提取的信号X1在4 s处出现波谷，在6 s处出现波峰，基本还原了水下目标磁场信号S的时域特征。图3(d)为X1的频域图，奇异值分解明显对信号非特征频段的能量进行了有效的抑制，从而有效地提取了目标信号。

将最优子信号Xi与磁异常信号进行互相关运算，结果如图4所示。当时延为0 s时，互相关幅值最大，在其他时延情况下，互相关函数的值明显低于0 s的值，有效验证了奇异值分解对信号波形提取能力。

如图5所示，对输入信号和加性白噪声进行奇异值分解，取一阶信号,其输出信噪比SNRout为1.07 dB。可以看出，奇异值分解对信噪比有明显的增益效果，且奇异值分解的方法能够有效地从特征频段中提取信号，从而恢复波形。

图3 奇异值分解的结果Fig.3 The result of singular value decomposition

图4 互相关函数Fig.4 Cross correlation function

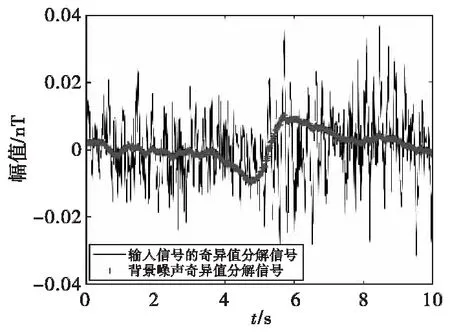
图5 最优子信号X1与背景磁场Fig.5 Optimal subsignals X1 and background magnetic field

一般来说，我们选择系统参数a=b=1，系统输出初值xi(1)=0。但为了系统更好的收敛效率，通过对参数的多次调整，取a=1,b=70。图6(a)为奇异值分解子信号Xi，同时也是随机共振系统的输入信号S+Γ。图6(b)是随机共振系统的输出x的波形图，可以看出，在目标信号出现的时间段4～6 s附近，输出x存在明显波动。图6(c)是检验统计量Y归一化后的波形图，截取窗长度N=300，以标准差作为检验统计量可以较好体现出是否出现目标。

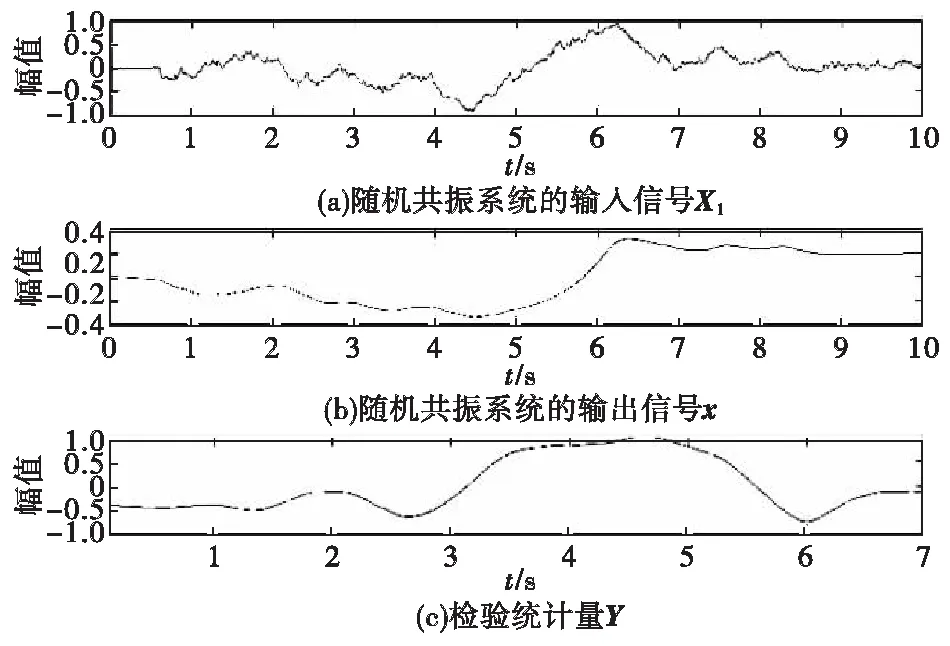
图6 随机共振系统的响应分析Fig.6 Response analysis of stochastic resonance systems

3 仿真实验

为了验证本算法的性能,分别对不同噪声强度D下磁异常信号的检测进行的仿真分析，并对无目标情况下的算法的输出进行了研究。图7对奇异值分解前后的输入信噪比SNRin、输出信噪比SNRout进行了不同条件下的仿真，其中磁异常信号强度不变，噪声强度D=1,2，…，5。可以看出，在低输入信噪比SNRin条件下，奇异值分解仍然能够较好地提高输出信噪比SNRout。并且当输入信号中不存在目标磁异常信号时，即输入信号仅为强度为D的高斯白噪声信号。

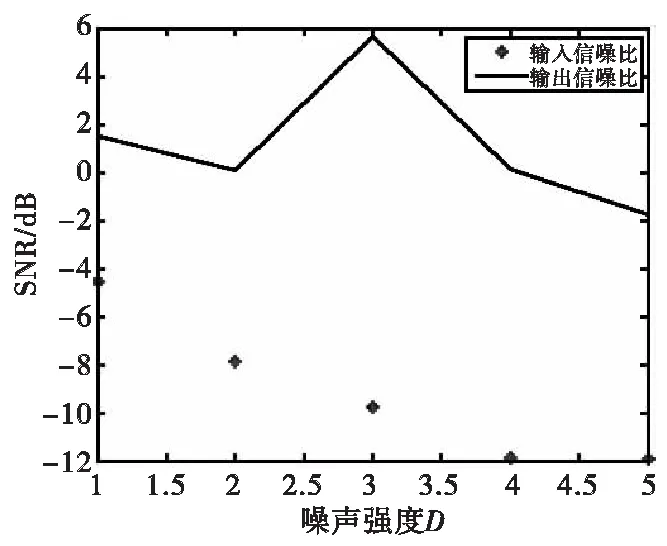
图7 信噪比变化图Fig.7 Variation of SNR

图8为在不同噪声强度D下，经过奇异值分解的最优子信号X1与磁异常信号进行互相关运算的结果。可以看出，互相关函数在时延为0 s达到峰值，即最优子信号X1基本恢复了信号时域特征。无目标时，输入为高斯白噪声，经过线性的奇异值分解，输出仍是高斯白噪声，并且与原输入高斯信号的互相关函数值为在0 s处的输出幅度较低。

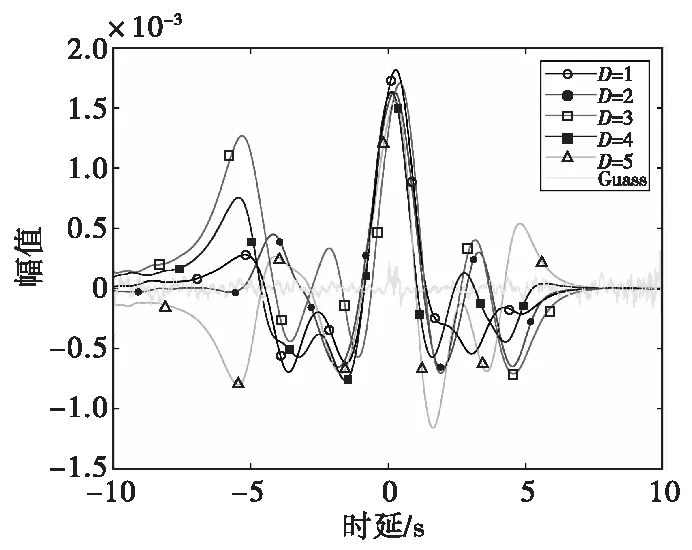
图8 互相关函数图Fig.8 Cross correlation function

图9为随机共振系统的检验统计量Y归一化后在不同时间的值，其中窗长度为N，随机共振系统结构参数a=1,b=70。可以看出，在不同噪声强度下，X1通过随机共振系统后的检验统计量能够较好的检测出信号。在6 s处，存在信号的同时，Y也达到了最大值；当不存在信号时，检验统计量Y仅为0.3，明显可以检测出不存在信号。

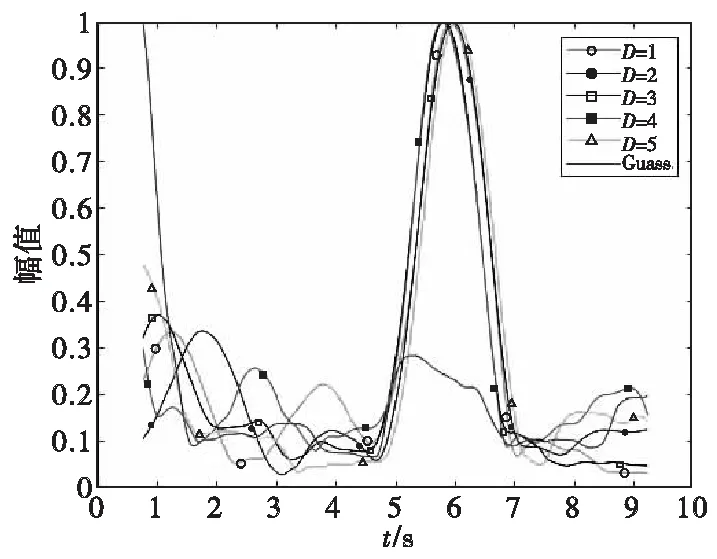
图9 检验统计量Fig.9 Response analysis of stochastic resonance systems

4 结论

本文提出了磁异常信号奇异值分解的随机共振检测方法。该方法将奇异值分解子信号通过随机共振系统，从强噪声中较好地恢复了水下目标信号的波形，并建立了有效的检测统计量。仿真实验结果表明，输入信号在信噪比仅为-12 dB时，经过奇异值分解，仍能较好地恢复波形，并极大地提高了信噪；随后通过随机共振系统后，亦能较好地检测信号。