基于SURF的图像配准改进算法
2020-05-18袁丽英王飞越
袁丽英,刘 佳,王飞越
(哈尔滨理工大学自动化学院,黑龙江 哈尔滨 150080)
0 引言
在20世纪70年代,随着美国对军事辅助导弹系统及飞行器的研究,图像配准的概念被首次提出[1]。目前,图像配准算法的研究逐渐由基于像素的灰度相关的趋势向局部特征相关发展[2],人们已经提出了各式各样的局部特征算法。SIFT即尺度不变特征变换算法[3],于1999年由D.G.Lowe等人提出,又于五年之后对此方法进行了改进[4],该算法对尺度缩放、亮度等变化具有良好的不变性。K.Mikolajczyk提出了Harris-Laplace 算法,该算法的优点是具有仿射不变性,但检测到的特征点较少[5]。H.Bay等人在分析总结多种特征检测方法的基础上提出了SURF(Speeded-Up Robust Features)算法[6],它加入了积分图像简化计算,减少了检测特征点的计算量,而且它对图像的平移、旋转、缩放等变化具有很好的不变性[7]。SURF算法是在SIFT算法已有成果上的改进。
尽管SURF算法具有杰出的性能,但仍然存在匹配精度低的问题[8]。产生这种情况的原因是:该算法是直接对原图像进行操作。原图像受到外界环境的干扰,获得的图像质量较差,提取特征变得困难,导致有效特征点的数量和准确度下降,从而影响匹配结果。本文针对此问题,提出了基于SURF的图像配准改进算法。
1 SURF算法
SURF算法由特征点检测、特征点描述和特征点匹配三部分组成[9]。通过积分图像建立特征点检测,选用Hessian矩阵检测子来检测特征点。利用特征点的Haar小波变换来寻找特征点的主方向,最终确定特征点的描述符[10]。通过描述特征向量之间的欧式距离,即相似度量以欧式距离作为准则,完成图像特征点匹配。
1.1 特征点检测
1.1.1积分图像
SURF算法中应用积分图像可将图像与二阶高斯微分模型卷积简化为对图像的加减,其中积分图像由Viola等提出[11]。积分图像任意一点(i,j)的积分值ii(i,j)定义为原图像左上角到任意点相对应矩形区域灰度之和[12],即:
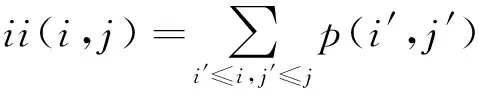
(1)
式(1)中,原图像点(i′,j′)的灰度像素的值由p(i′,j′)表示,可由式(2)、式(3)迭代得到:
S(i,j)=S(i,j-1)+p(i,j)
(2)
ii(i,j)=ii(i-1,j)+S(i,j)
(3)
式(2)中,S(i,j)表示一列的积分。对于超过边界的值,令S(i,-1)=0,ii(-1,j)=0 。只需要对图像所有像素扫描一遍就能求解积分图像[13]。
当求解图像W内的全部像素灰度时,可以不考虑W的大小,使用积分图像的四个相应点(i1,j1),(i2,j2),(i3,j3),(i4,j4)的值加减可得,如图1所示,即:求取W内的像元灰度和跟W的大小不相关。W内的像元灰度和∑W即:
∑W=ii(i4,j4)-ii(i2,j2)-ii(i3,j3)+ii(i1,j1)
(4)
若有一幅图像的灰度值均为1,则图像中任意点(i,j)积分图像的值就是从该图像左上角到它所组成的方形区域的大小,则W组成的方形的面积为∑W。
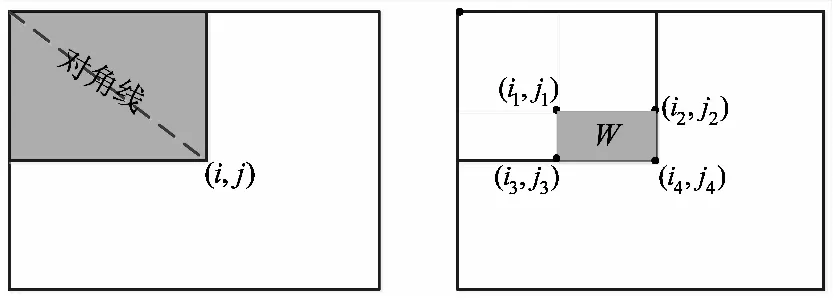
图1 积分图像的计算和窗口内像元灰度求和Fig.1 The calculation of the integral image and the pixel gray-level summation in the window
1.1.2确定特征点
尺度空间理论是特征点检测的基础。通过积分图像加快图像卷积来增加计算速率。然后通过计算图像每一个像素的Hessian矩阵行列式获得特征点的值[14]。Hessian矩阵是以二阶偏导数矩阵组成的,给定图像I某一点(x,y)处Hessian矩阵即:
(5)
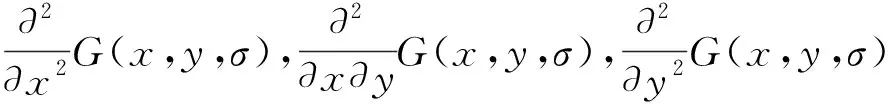
(6)
式(6)中,⊗表示为卷积,二维高斯函数如下所示:
(7)
H(x,y,σ)的行列式值Det(H)如下:
(8)
1.2 特征点描述
为了确保特征点的旋转不变性,需要给所有特征点分配主方向[15]。具体步骤为:
1) 选取特征点为圆心,在以半径为6s(s为特征点所在的尺度)的圆形区域内,对图像进行Haar小波响应运算[16],根据间隔距离,对得到的响应值赋,然后统计响应直方图[16]。由于使用了积分图像,使得计算速度加快。 尺度s的计算方法如下:
(9)
式(9)中,Sizecurrent-Filter、SizeBase-Filter和ScaleBase-Filter分别表示当前滤波尺寸、基准滤波尺度和滤波尺寸。
2) 通过60°的扇形滑动窗口,以步长0.2弧度两侧,旋转这个滑动窗口,如图2所示。对图像的Haar响应的dx、dy进行叠加[16],生成矢量(mw,θw)即:
(10)
(11)
当mw在窗口内的叠加值最大的时候,其角度θw对应主方向。

图2 滑动窗口围绕特征点转动求取主方向Fig.2 Sliding the window around the feature point to find the main direction
3) 特征点主方向确定后,在特征点周围20s×20s的矩形内计算特征描述子。将此矩形化分成4×4子区域,使用尺寸为2×2模板的Haar小波计算每个子区域x方向和y方向的Haar小波响应值。
1.3 特征点匹配
特征提取得到两个特征点集合后,可根据特征点间的相似性度量来进行匹配,因为SURF特征向量维数不低[17],一般都采用欧式距离作为相似性度量准则。
1.3.1最小距离法
参考图像I1和待配准图像I2的特征点描述符分别为x=(x1,x2,…,xi),x′=(x1′,x2′,…,xi′),则x和x′间的欧式距离如下:
(12)
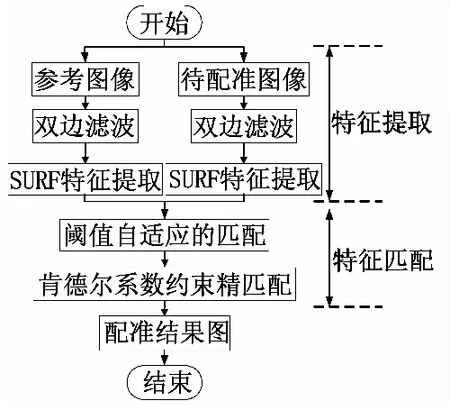
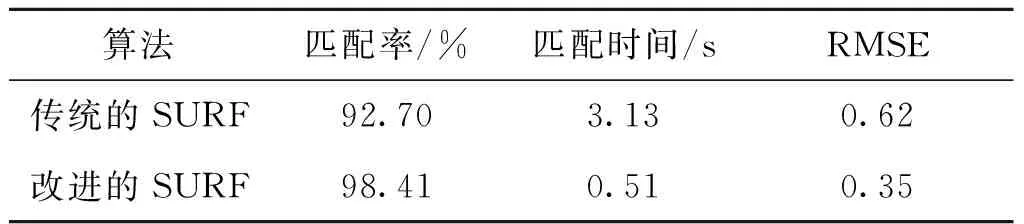
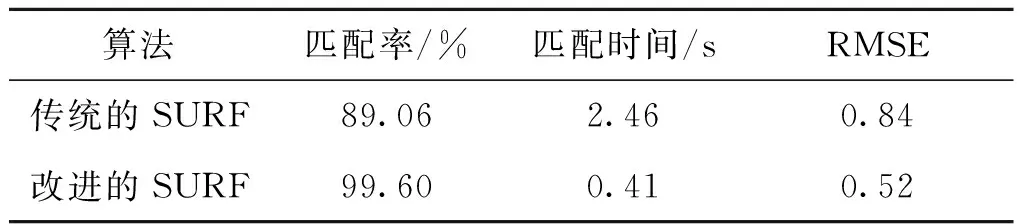
算出待配准图像与参考图像的所有特征点之间的距离,选择与之相距最小的特征点作为匹配对。图像中所有特征点都进行同样的操作,得到全部的特征匹配对。dmin为所有匹配点对距离的最小值,阈值设置为T=μ×dmin,剔除匹配点对中d 1.3.2最近邻与次近邻比值法 由式(12)计算出来的I1和I2所有特征点对间的距离,若在图像I1内的特征点与图像I2内距离最近和次近点间的距离分别为dmin,dsecond,则设定一个阈值T且满足如下: (13) 通常,T的取值为[0.4,0.8],即最近点与次近点相比有更大的优势时才能构成匹配对。 获得特征点匹配对之后,使用RANSAC算法[18]求解仿射变换模型,具体分以下几步: 1) 任意选三个特征匹配对,计算变换参数集P,初始化匹配对数matcher为零; 3) 若matcher超过某个阈值N,则终止计算,否则转到2); 4) 若计算完所有的特征点对时matcher都没有超过N,那么就将matcher为最大值时的集合P作为最后的参数集合。 通常情况下,误差d的取值范围为1~10,若特征匹配集合的最大数量为M,阈值N与M的关系为N=4/M。事实上,若初匹配阶段特征点的准确匹配率超过40%,则算法会很快收敛。 本文对传统的SURF图像配准算法的特征点提取以及特征点匹配进行改进。其具体流程图如图3所示。 图3 SURF图像配准算法改进流程图Fig.3 Flow chart of improved surf image registration algorithm 一般的低通滤波器只考虑其中的灰度相似关系,将可能的边缘信息和噪声都滤掉,造成边缘信息缺失,致使边缘模糊。为了提取更好性能的特征点,本文预先采取双边滤波的形式,对图像处理。双边滤波器兼顾了像素点周围的空间邻近、灰度相似关系,能够解决滤除边缘问题[19]。双边滤波HBL如下所示: (14) 式(14)中, (15) 式(15)中,x为当前位置,y∈s是以x为中心的s×s区域内的点,Ix,Iy分别代表对应的像素值,‖x-y‖为空间距离,Gσd,Gσr分别表示空间近邻函数和灰度相似函数,Gσd能够避免远距离像素的影响,Gσr可有效避免像素值突变的干扰。具体定义分别如下所示: (16) (17) 式(16)中,d(x,y)为图像两像素点间的欧式距离,σd,σr为高斯函数标准差。式(17)中,δ(I(x),I(y))为Ix,Iy间的灰度差。σd,σr分别限定像素位置的空间和灰度变化来控制滤波效果,σd,σr决定了双边滤波的性能。σd,σr值的选取可以根据实际情况调节。 SURF特征点使用最近邻域和次近邻域法进行匹配时,阈值的选取会对匹配结果产生影响,进而匹配精度也会受到影响。 2.2.1阈值自适应匹配 本文并没有选取固定的阈值去完成匹配,而是通过阈值自适应约束对初始匹配特征集合进行筛选。步骤如下: 1) 假设从基准图和待检测图像中获得的初始特征集合分别为X,Y,计算X中任意点和Y内的全部特征点间的距离di,并将di按照从小到大的依次排列; 2) 对X中的所有点都进行第一步的操作,并分成n组; 3) 对上一步中得到的n组数据,分别计算每组中在最前面的两个数据的大小之比Ti(i=1,2,…,n); 4) 计算Ti的平均值Td,设正确匹配对为match=0,初始化阈值为Tr=Td(0 5)若检测到的点的最近和次近邻域之比小于Tr,则++match对,可能是周边相近的比较多,为了减少误匹配,则Tr=Tr-0.05。反之,连续几次都没有检测到正确的匹配对,则Tr=Tr+0.05,直到所有的特征点检测完成为止。 2.2.2肯德尔系数约束 初匹配得到的特征点也会有错误匹配,若图像在拍摄时受到干扰,错误匹配会更多,对配准精度有更大的影响,所以本文采用肯德尔系数约束实现精匹配,从而减少误配率。 设SURF算法通过初匹配得到的点在待配准图像中的中心位置为K,尺度为σ,主方向为ω。给特征点定义一个半径ρ,且半径ρ=6σ。采用特征点为核心、建立边长为S=round(α×ρ)的正方形,α为实验参数[20]。 如图4所示,设P1是图像I1的配准点,且其中心位置点、尺度、半径、主方向分别为K1,σ1,ρ1,ω1,其周边正方形区域为Rec1,边长为S1=round(α×ρ1),同理,则对应到图像I2的点为P2,且K2,σ2,ρ2,ω2,S1分别对应着P2的中心位置、尺度、半径和主方向及P2周围正方形区域Rec2的边长。其中S2=round(α×ρ2)。 图4 特征点对应的正方形区域Fig.4 Squares corresponding to feature points 当图像旋转时,对应的正方形也应该做出相应旋转,则P1,P2主方向之间相差角度Δφ如下: Δφ=ω1-ω2 (18) (19) Aij即可表示为如下所示: (20) 式(20)中,Aij为0的情况有三种,第一种为:v1i-v1j=0且v2i-v2j≠0,第二种为:v1i-v1j≠0且v2i-v2j=0,第三种为:v1i-v1j=0且v2i-v2j=0。 肯德尔系数τ表示为: (21) 式(21)中,C,D分别为Aij等于1,-1的次数,T(v1i-v1j)=0,(v2i-v2j)≠0的次数,U为(v1i-v1j)≠0,(v2i-v2j)=0的次数。 为了求解每对配准点的肯德尔系数,需要设定一个阈值TKτ,当TKτ小于τ时,则此配准点对是较强的匹配对;当TKτ大于τ,则舍去配准点。TKτ的计算如下: TKτ=mean(Mτ)-std(Mτ)/2 (22) 式(22)中,mean(Mτ),std(Mτ)分别对应肯德尔系数的均值和标准差。 本实验的目的是对传统的SURF算法与改进后的SURF算法进行比较,选取不同视角拍摄的图像与变换程度不同的图像,针对配准时间、配准率以及RMSE(均方根误差)等方面进行分析。实验环境为:Windows7操作系统,酷睿i5-3230M,CPU Intel 2.6 GHz,内存4 GB,使用Matlab2014(64位)软件。 选取同一场景不同角度拍摄的两幅图像,分别采用传统的SURF算法和改进后的SURF算法进行实验,如图5所示。 图5(c)与图5(d)对比可以得出,改进之后的SURF配准算法与原来的算法相比配准精度损失不明显,但是明显去掉了部分误匹配点对,提高了匹配的精度。实验数据记录如表1。 根据表1,通过匹配率、匹配时间以及均方根误差可知,改进的SURF算法匹配率提高了,证明改进的图像配准算法能够提高配准的精度。且改进算法的匹配时间也较短,所以改进的SURF算法实时性好。 图5 SURF图像配准算法改进前后的匹配结果Fig.5 Matching results before and after improvement of surf Image Registration algorithm 表1 算法改进前后配准结果对比 Tab.1 Comparison of registration results before and after the improvement of the algorithm 算法匹配率/%匹配时间/sRMSE传统的SURF92.703.130.62改进的SURF98.410.510.35 选取同一场景不同变换程度的两张大山图片,分别使用改进前后的算法进行配准,实验结果如图6所示。图6(a)、图6(b)分别为参考图像和待配准图像,图6(c)、图6(d)分别为算法改进前后的图像特征点匹配。 图6 SURF图像配准算法改进前后的匹配结果Fig.6 Matching results before and after improvement of surf Image Registration algorithm 图6(c)中结果的重叠的部分比较明显,造成部分信息丢失,因而得到的结果相较于图6(d)而言,图像信息没有得到充分的利用,图6(d)的配准视觉效果更佳且提高了配准的精确率。实验数据记录如表2。 表2 SURF算法改进前后配准结果对比 由表2可知,改进后的SURF算法匹配率接近100%,因而改进后的算法对误配点的提纯起到作用,匹配时间减少,且均方根误差也降低,证明改进的算法提高了配准精度。 本文提出了基于SURF的图像配准改进算法,该算法针对SURF图像配准算法存在配准精度低的问题,在特征点提取之前采用双边滤波,有效的抑制一些不相关的特征点和噪声误差。阈值自适应的约束对得到的特征点进行初始匹配,提高了正确匹配对的精度。肯德尔系数可以对误配点进行二次剔除。实验结果表明,改进的SURF算法配准精度与鲁棒性增强,并且匹配时间减少。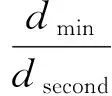
2 改进的SURF算法
2.1 特征点提取的改进
2.2 特征点匹配的改进

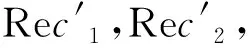
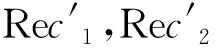
3 实验结果及分析
3.1 不同视角的图像配准实验

3.2 变换程度不同的图像配准实验

4 结论
