再谈“弧度制”教学

石志群

笔者在1994 年曾经写过一篇关于“弧度制”教学的文章，提出了一个弧度制教学的建议，现在想来，还是存在一些问题，而且是比较重要的问题。下面是笔者经过多年的学习和研究后的一点体会。

一、对“角度制”的认识

角度制是一种常用的角的度量制，究其原因，可能与其产生的背景有一定关系。据查相关数学史料，角度制起源于古巴比伦，可能与历法有关。我国数学史专家李文林认为，取圆周的三百六十分之一弧所对圆心角为角度制的单位（1°）的原因可能是因为“360”的因子较多，便于细分，其中角度制的进位标准“60”就是其因子之一。

应该说，角度制能够解决与角有关的很多问题，这种制度已经深入我们生活的方方面面，以否定角度制的价值作为引入弧度制的理由是不恰当的。不仅如此，角度制反而是引入弧度时说明其合理性的理论依据，是思维的基础，并且通过角度制与弧度制的互化，也可以进一步强化学生对弧度制的认识与认同。

二、为什么要引入“弧度制”

首先，作为度量制，本身就应该是丰富多样的，以适应不同状态下使用的方便。比如，长度的单位有毫米、厘米、分米、米和公里，这是现实生活中常用的长度单位；而在微观世界，却需要纳米这样的长度单位，在天文学中又需要光年作为度量距离的单位。因此，在角的度量方面也需要不同的度量制，以适应不同状态下的使用便利。事实上，度量角的制度并不是只有角度制和弧度制两种，比如密位制、百分制都是角的度量制度。

其次，在弧度制下，许多数学结论的结构形式显得非常简单，而在角度制下却比较复杂，而且从推导过程看，前者也比后者要容易得多。比如，在弧度制下，我们有下面的结论：

而在角度制下，对应的关系是

而像sinx，cosx 等三角函数的泰勒展开的级数表示式，角度制下的形式比弧度制的形式更加复杂，推导的难度也更大。

出现上述区别的原因就在于，在两种不同的度量制下，式子中出现的不同量的量纲的差异。在角度制下，角的量值的进位制为60 进位，圆的半径、弧长的量值是实数，其进位制为十进位。而“统一”是数学学科的基本审美追求，这也成为引入弧度制的一个重要的依据。

三、“弧度制”的教学定位

“弧度制”作为“三角函数”一章的组成部分，其教学定位取决于它在章节中的功能、目的（价值）。

如果从量纲考虑，这些式子中表示角的大小的α 在角度制下为60 进位，而实数x，y，r 却以10 进位，不同的进位显然不利于数学的研究。而作为函数，是在数集之间建立的对应关系，将角度制下的自变量α 作为函数研究必然遇到麻烦。因此，“弧度制”一节内容的教学定位应该是“建立一种角的度量制，将表示角的大小的值‘数量化’（变成十进制）”。

四、“弧度制”的认知难点

“弧度制”经常被一些教师称为“糊涂制”，就是指学习的认知难度比较大，学生常不知其所以然。笔者经过多年观察和分析后发现，学生的认知困难主要有以下几个方面：

一是与已有的度量制的习惯不一致而导致认知困难。长度、质量等度量制是学生比较熟悉的，而这些量的度量体制有一个共同特点，就是用“自己”度量“自己”，即用长度度量长度、用质量度量质量。具体地说，用一个长度作为度量单位，在度量时以其为基础进行“整除”，对于余数，再用单位的十分之一进行“整除”，……如此下去。角度制尽管不是十进制的，但其仍是用“自己”度量“自己”的定义方式，学生容易理解，但是，弧度制却是用“长度”度量“角”（单位圆时，即弧长），这是学生第一次接触到这样的定义方式，认知有困难是可以理解的。

二是角度制是用一个确定的“单位”（1°的角）进行度量，容量理解，而弧度制中对不同的圆，度量的直观意义不明显，学生有一种半径大小不同，度量的单位就不一样的感觉，从而觉得弧度制下好像没有“单位”一样，由此产生困惑。

三是学生不理解为什么要引进弧度制，因为它的好处（优点）要在学习过微积分等内容后才能体现出来，现在教学中教师通常由弧长与半径之比只与圆心角的大小有关就直接下定义，学生产生疑问：为什么可以用这个比表示大小就一定要建立一种新的度量制呢？优越性、必要性没能体现，学生对弧度制有一种不太愿意接受的抗拒心理。

五、怎样自然地引入“弧度制”

在《从“弧度制”一课谈概念课教学原则的实施》一文中，笔者是在复习角度制（角度制的建构方法与过程）的基础上，由学生熟悉的圆周率发现“圆的周长与半径之比为常数”，进而推出“周角对应的弧长与圆的半径之比为常数”的结论，再提出一般性的问题：对一个确定的圆心角，其弧长与半径之比是否为定值？通过计算可以发现确有此结论，从而为引入弧度制建立了理论基础。在此基础上提出问题：能否根据这一性质，建立一种新的度量角的“制度”。现在想来，这个方案还是没有解决“为什么要建立弧度制”这个非常重要的问题。

笔者在苏教版高中数学教材的编写过程中，受到教材组专家们的启发，对“三角函数”一章的内容，特别是弧度制这个知识点，得出了上文中的一些认识。在此基础上，笔者进一步发现：既然三角函数是刻画周期现象的数学模型，其反映的其实是α，r，x，y 之间的关系，那么现在要解决的问题其实就是如何在“构建刻画周期现象的数学模型”这个大的框架下，明确弧度制在其中的地位和作用，明确其与三角函数概念建构之间的内在联系，换言之也就是将与α大小有关的量弧长l 也放到与α，r，x，y 一致的位置，探寻它们之间的关系。这就是苏教版教材“三角函数”一章章首语的内容：周期现象→圆周上一点P 的运动→点P 的数学刻画→α，r，l，x，y 之间有着怎样的关系？由此得到本章的研究路径：任意角（要能“周而复始”，角的概念就要推广）→弧度制（α，r，l 之间有着怎样的关系，角的度量要实数化）→三角函数的概念（α，r，x，y 之间有着怎样的关系，由α 为锐角时想到了三角函数，从而推广到任意角的情形，得到刻画周期现象的数学模型）→这个模型是如何刻画周期现象的，具有怎样的性质……

再考察第2 节中所研究的引入弧度制的必要性，抓住两个关系要素——求简和求统一，进而设计出本节内容的教学过程。以下为本节课的主体部分，供各位同行参考。

1.问题情境。

师：在章首语中，为了刻画周期现象，我们选择了最简单的原型：圆周上一点的运动。为此我们分别用（r，α）、（r，l）（α，l，r 分别为圆心角的大小、所对弧长、半径）及（x，y）来刻画圆周上点的位置（见章首语中图），并提出了本章初始问题：α，l，r，x，y 之间具有怎样的关系？

为了刻画“点P 在圆周上‘周而复始’的运动”，我们对角的概念进行了推广。今天我们一起来考察r，l 与α 之间具有怎样的关系。

2.数学建构。

（1）关系分析。

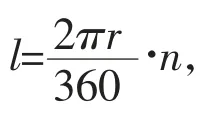
师：这个式子反映了r，l 与α 之间的何种关系？

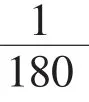
由学生探求。

（2）建构新知。

由学生根据推导过程发现：系数中的“360”是由角度制的单位的选定所决定的。

（板书：角度制下，关系比较繁）

师：在这个式子中，弧长、半径都是实数，它们是多少进位制？圆心角α 是多少进位制？

……

师：这说明，在角度制下r，l 与α 之间不仅关系繁，而且进位制也不一样。

（板书：α 与l，r 的进位制不同）

师：那么，能否建立一种新的角的度量制度，使得r，l 与α 之间的关系显得更加简单，而且三个量的进位制又得到统一呢？如何使得关系“简单”？

师：如果这样定义，这个角的度量制度的单位是什么？

由学生独立思考，完成建构。

师：角度和弧度都可以表示角的大小，那么它们之间有着怎样的关系呢？比如：60°的角是多少弧度呢？1°的角是多少弧度？1 弧度是多少度？-60°是多少弧度？……

（完成弧度制的完整概念）

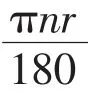
学生独立完成后，说明：较角度制，这两个公式均显得简单，弧度制确定起到了化繁为简的作用。那么：

师：弧度制下，α 与r，l 进位制是否统一？

由学生思考，可以发现，进位制统一了。

师：这里，r，l 分别表示线段与弧的长度，请大家思考一下，是否存在某个特殊的圆，使得圆心角的弧度数也是某线段或弧的长度呢？

教师基于学生的讨论，构建图1。

通过单位圆及图1，引导学生认识到：角的概念推广以后，在弧度制下，角的集合与弧度数的集合之间建立起一一对应关系，即角的集合与实数集R 之间建立起一一对应关系：每一个角都对应唯一的一个实数；反过来，每一个实数也都对应唯一的一个角。通过图1，让学生建立弧度制下的“角”的大小的“实像”——单位圆上对应的弧长——这对克服认知困难有一定的帮助。

上述过程，以“使角的度量值为十进制的实数”为目标，以求简和求统一的数学审美观为导向，以学生为建构的主体，将“弧度制”一节的内容置于全章的统一框架下，不仅使本节课的内容构成一个完整有机整体，而且凸显了单元的整体结构，让学生从整体中感受到“弧度制”在“三角函数”一章中的奠基作用。