基于DDC算法的可见光通信的非线性补偿技术

黄绪发

（上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引言

可见光通信（Visible Light Communication，VLC）是一种利用可见光波段的光作为信息载体，不需要光纤等有线信道的传输介质而直接在空气中传输光信号的通信方式[1]。目前，已有的非线性补偿技术可分为预失真补偿技术和后失真补偿技术。在非线性预失真方面，文献[4]首次设计了一个只包含二极管和电阻的预失真电路，对系统非线性失真进行补偿，该系统存在过于简化的问题。在文献[5]中，Elgala测量了LED的前向电压和前向电流，并评估了电压电流反向特性曲线，通过在发送端增加物理设备来实现预失真，该方法忽略了LED非线性的记忆问题。后失真技术方面，文献[6]提出一种叫做多模改进级联的后均衡算法补偿系统的线性失真，该方法优点能将系统的误码率降到阈值之下，缺点当系统的调制阶数较高时，无法处理系统的非线性失真。

近来基于聚类的传统算法 K均值聚类算法（K-means cluster algorithm，K-means）被提出用于解决 VLC系统中的由 LED引起的非线性失真[3]。但是其存在问题是当可见光的非线性较大且信号较为聚合的时，若信号的聚类中心偏离了原有的区域，该算法将会陷入局部最优解。基于此，本文提出一种新的密度聚类算法（Density and distance-based clustering，DDC）[2]解决VLC系统中的非线性问题。DDC算法是一种基于密度的聚类算法，它的主要思想是找出每簇中密度最大的点作为聚类中心。仿真结果表明，在非线性较大时，DDC算法的性能较于K-means算法在误码率方面得到很大的改善。

1 系统模型

对室内可见光通信进行理论建模。可见光的传播分为视距传播（line-of-sight，LOS）和非视距传播（Non-LOS，NLOS）。由于可见光的超高频率的高路径损耗，使得室内可见光通信的信道测量具有很强的稀疏传播特性。与传统的室内无线信道相比，室内可见光的传播主要依赖于视线范围（LOS）路径，文献[9]中指出，在NLOS传输情况下，其反射链路的最强信号强度比LOS链路信号强度最弱情况下低最少7 dB，基于此，本论文中仅考虑LOS传输情况。

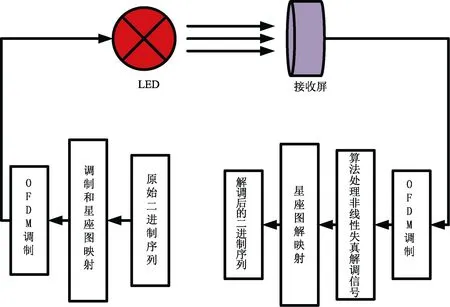
图1 信道模型Fig.1 Channel model

建立如图1所示的可见光传输模型，PD是光接收器，本文仿真的系统为一路发送一路接收的可见光系统，发送端经过星座映射后，然后进行OFDM调制[7]，用加性高斯白噪声模拟实际传输中的噪声。根据文献[10]可知，信道增益ijh可以由下式表示：

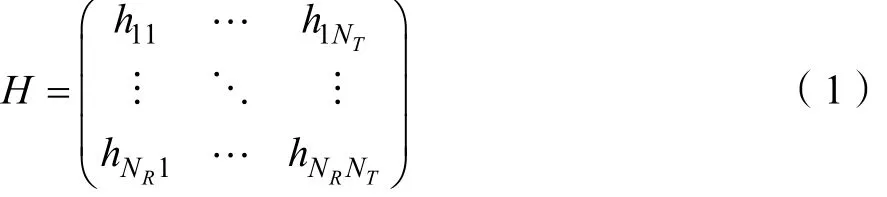
hij表示的是第j个LED灯到第i个PD的信道增益。收发信号的频域关系表达式可表示为

其中X表示发送信号，Y表示经过信道传输后的接收信号，H表示信道矩阵，N为加性高斯噪声。

接收端经过OFDM解调后，对信号进行基于最小二乘法估计准则的频域均衡，可表示为

式中X表示经过信道均衡后的信号。然后用DDC算法对均衡后的信号值进行聚类，将聚类中心作为更新的星座映射点。相比原始的星座映射点，更新后的星座点包含了非线性的影响，因此根据其对均衡信号进行星座解映射，能有效降低可见光通信系统非线性。

2 算法聚类原理

造成VLC系统非线性的原因有很多，包括PIN光电探测器、发射机驱动电路和放大器。因此，利用机器学习模型对整个 VLC系统的非线性进行补偿是一种可行而有效的方法。基于机器学习的感知决策模型适用于采用归纳法而非演绎法对失真信号进行补偿。考虑到系统中信号星座点的分布具有集聚性，利用调制点周围具有较高的密度，不同较高密度星座点间具有较大的距离的特点，相比 K-means聚类算法，因此采用基于密度的算法（DDC）更为有效。

DDC算法原理的核心是两个指标，一个是样本点的密度 ρ；另一个是任意一个样本点与比其密度更高的样本点的之间的最小距离 σ。密度和最小距离的计算方法如式（4）和式（5）所示：

用加入高斯的白噪声的 16阶正交振幅调制（16Quadrature Amplitude Modulation，16QAM）调制信号作为测试信号.我们称由公式（4）得到距离和公式（5）得到的密度构成的图为星座的决策图。位于决策图左上角的星座点为 DDC算法聚类出的中心点，从决策图中可以看到利用DDC算法可以有效的聚类16AQM调制信号。

图2 16QAM决策图Fig.2 16QAM decision diagram

准确的找到聚类中心后，怎样利用准确的聚类中心降低系统的非线性？为了便于阐述，我们基于[3]中的可见光通信非线性星座图画出系统产生非线性的信号的接收星座图（图 3），从[3]中可知，系统的非线性主要是由于外围的星座点能量过高导致星座点发生旋转和幅值的衰减，使得系统产生非线性失真，导致系统的误码率升高。图3，4说明了准确找到聚类中心点的意义，可以将大量失真的信号点平移到正确的位置上（即调制位置），使得信号得以准确的解调，从而降低了非线性系统的误码率。

图3 产生非线性的的星座图Fig.3 Nonlinear constellation

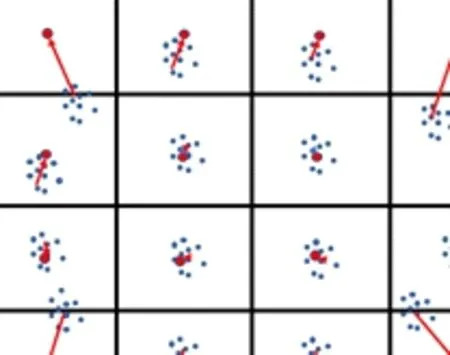
图4 非线性修复示意图Fig.4 Non-linear repair

根据上述原理，DDC算法步骤可分为以下六个步骤。

第二步：通过在每个样本点周围 D%的样本点的数目来确定密度截断距离dc。

第四步：根据公式 2，计算每个比样本点局部密度高的最小距离

第五步：通过步骤三和步骤二画出决策图。在决策图中，取出右上角的K个点作为聚类中心点。

第六步：将非聚类点分配到各自的聚类中心，然后进行修正。

3 实验仿真和结果分析

根据文献[3]，我们在仿真中模拟了系统的非线性效应，根据可见光通信非线性的特点，只对位于星座图中四个角的信号进行非线性处理,用来模拟可见光通信的非线性失真，为了便于叙述用x表示星座图上四个角的信号，偏移量公式（6）为：

其中y非线性处理之后的信号，其余的信号未进行非线性处理，αi是具体的偏移量，i∈｛1,2｝,α= { (0.8,0.9),(0.8,-0 .9),(-0 .8,0.9),(-0 .8,-0.9);(0.6,1.3),(0.6,-1.3),(-0.6,1.3),(-0.6,1.3)}。即α1表示偏移量为（|0.8|，|0.9|），2α偏移量为（|0.6|，|1.3|）。在未进行归一化的情况下，16QAM在仿真中的有效解调范围是2，所以我们设置一组的偏移量小于1，另一组偏移量大于 1，用这两种方式来模拟文献[3]中的非线性。由于在[3]中处于边缘的信号受到的非线性较为严重，有的位于解调有效范围内，有的位于有效范围外，因此我们设置了这样的信号偏移量公式。本文的仿真实验的条件如下：发送端采用 16QAM调制，利用偏移量公式对信号进行非线性的处理，然后采用OFDM调制，OFDM的子载波数为256个，循环前缀是子载波数的1/8。

图5两种不同非线性情况下，发送信号星座图的信号分布情况。根据文献[8]，在室内均匀光照下，接收端最小信噪比可以达到20.12 dB，在1 m的范围内可见光通信的信噪比高达 27 dB，因此本实验采用信噪比范围设定为20-30 dB之间进行仿真。聚类的效果图如图6。

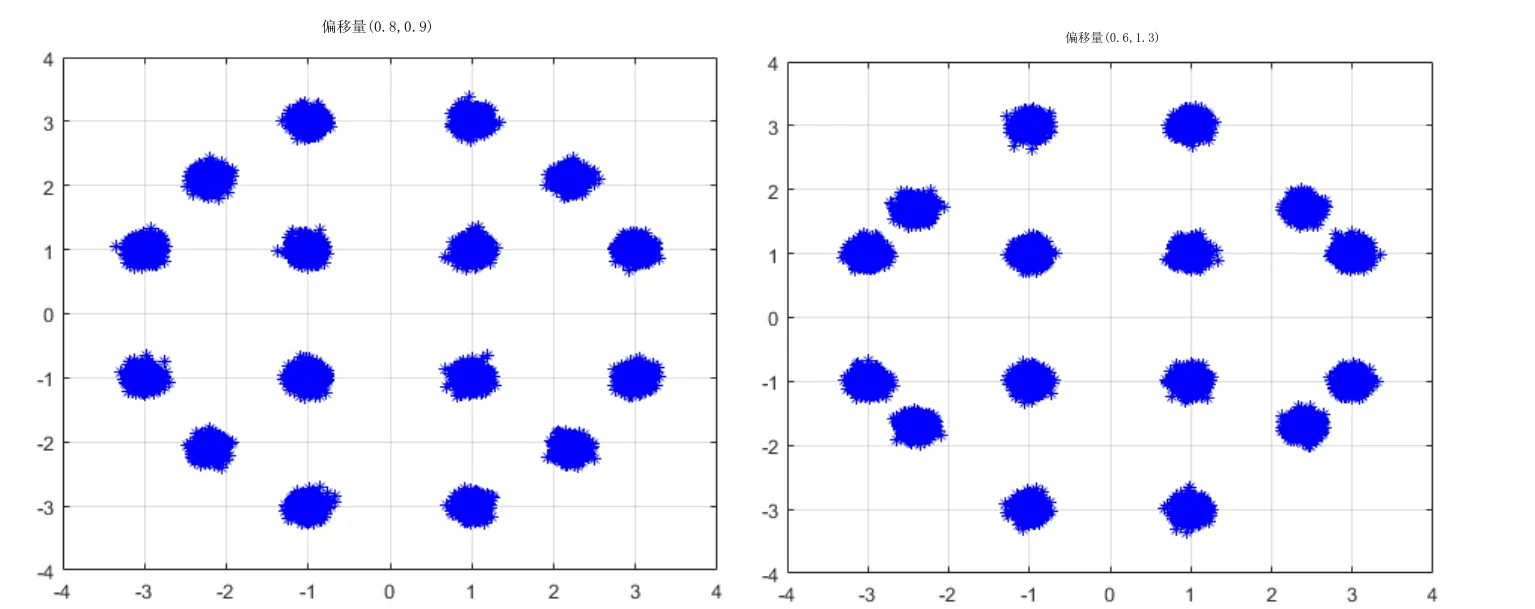
图5 不同非线性程度的发送信号的星座图Fig.5 Different degrees of nonlinearity

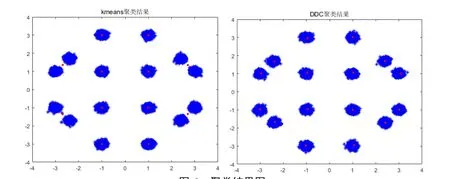
图6 聚类结果图Fig.6 Clustering results

从聚类的结果图可以很清楚的看到，K-means聚类出现了严重的问题，这组实验中我们采用文献[3]中采用的初始化聚类点的方式，以标准星座点作为初始聚类点。Kmeans算法初始化聚类的方式有很多，另外一种常见的初始化方式是采用随机初始化的方式。文献[2]中具体阐述了随机化初始聚类点次数与最优选择策略之间的定量关系，当聚类点数增多，若采用一次随机化，性能非常差，要满足较大概率的最优策略，则必须增加随机化的次数，这个次数与簇的数量之间为指数级别的关系，计算复杂度过高。本仿真采用的初始化是基于通信调制系统的特点，采用第一种初始化的方式。当可见光通信系统的非线性过大时，采用非线性情况2α进行模拟。此时，根据K-means聚类的原理，由于所有的星座点与四个角的簇的距离相对于其他簇的距离均不是最小值，采用K-means聚类会出现少簇的情况。而采用DDC算法则不会出现这种问题，DDC算法依然可以准确地聚类出信号。从聚类结果图中，能直观的看到为什么 K-means算法在处理非线性较大，信噪比较高的情况下性能比DDC差。

当非线性较为严重的时候，如图7（2）所示，在信噪比低于23 dB时，K-means与DDC相差无几，但是当信噪比大于23 dB时，原本位于星座图四个角的信号由于非线性的影响发生的错区现象，即全部信号落入的别的星座调制区域。根据之前的假定，我们K-means算法选取的初始聚类点为16QAM标准星座调制点，由K-means聚类的聚类过程可知，此时位于四个角的信号将不会正确的判定，所以当信号完全错区时，使用K-means算法与不用任何算法，误码率结果时一样的，从仿真结果图也证明该结论，K-means由于将原来的16个簇变成了12个簇，因此导致误码率没有得到改善。DDC算法由于采用的是基于密度的算法，与初始的聚类点无关，因此当信号发生错区情形时，DDC算法依然能够准确的聚类出16簇，因此能大大降低可见光系统的非线性，从而使得系统的误码率降低。图7是两种不同非线性情况下，DDC算法和K-means算法的误码率比较图，其中w/o表示系统不使用任何算法系统的误码率表现。

4 结论

图7 非线性程度对于系统误码率的影响Fig.7 Bit error rate of the system

本文提出了基于密度的 DDC算法用来解决可见光通信系统中的非线性问题。DDC算法基于簇内必存在密度最大的点，密度大的点之间的距离较远的想法，能够准确的找到接收星座图的聚类中心，从而降低了可见光通信的误码率。其优点是，能很好地解决可见光通信的非线性问题，误码率较低，在信噪比超过22 db时，能将严重失真的信号，进行准确的解调，误码率达到10–5级别以下。DDC算法比于K-means算法，能处理可见光通信系统产生非线性失真更严重的情况。DDC算法也存在自身的局限性，对信号的信噪比有一定的要求，当数据量大的时候，运行时间过长，所以进一步优化DDC算法是我们的下一步目标。