求解考虑机器调整时间的并行机分批优化调度问题

2020-05-16孙思汉陶翼飞董圆圆王加冕

软件 2020年4期

孙思汉，陶翼飞，董圆圆，张源，王加冕

（昆明理工大学机电工程学院，云南昆明 650000）

0 引言

其实车间调度问题[1]（Workshop Scheduling Problem，WSP），讲的是在实际生产环境和外界突发因素的影响下，根据生产车间所提供的物资[2]按照一定规则进行恰当且符合实际生产的分配，用以确保能够搜寻到任务所需的优化目标。目前对并行机优化调度[3]（Parallel Machine Optimal Scheduling，PMOS）的研究不仅对企业的实际生产还是对研究人员，都有着重要的实际意义和理论价值。现阶段，关于PMOS的研究，多数文献中都是选用智能搜索算法[4]对模型进行仿真求解，目前已广泛应用于企业生产所面临问题的求解中。灰狼差分进化混合算法是将经典灰狼算法[5]（Grey Wolf Algorithm，GWA）、差分进化算法[6]（Differential Evolution Algorithm，DEA）进行局限性互补的智能优化混合算法，主要是模仿狼群的捕猎行为，将求解最优目标抽象成狼群的狩猎行为，同时又具有遗传、迭代等选择操作流程的行为，具有避免其陷入局部最优，防止过早收敛状况、可调参数少的优点。目前国内已有文献大多研究的是GWA和DEA单独改进的算法，应用于求解企业项目中资源调度、函数优化等问题[7]中，而对于灰狼差分进化混合算法应用到相关生产中的研究仅是对约束条件进行简化，往往忽略了工件在机器上的调整时间，使得算法的寻优精度和效率有所降低。因此，本文结合实际工况，以生产过程中系统运送工件和机器安装不同的工件所产生的生产辅助时间为研究对象，引入灰狼差分进化混合算法，建立PMOS并行机模型，并以最小化最大完工时间作为 WSP的优化目标和验证灰狼差分进化混合算法的性能指标。

1 考虑机器调整时间的并行机分批调度问题描述

现假定并行机生产车间要对若干个工件进行分批加工，其中，工件有N种，每种工件有Gi个，每一种工件皆为一道工序进行加工生产，即单工序加工。车间可提供的M台加工机器，加工工件可以在所安排的M台机器设备中的任意一台上进行加工，同时同一台机器加工不同种工件时需要对机器进行调整，产生相应的调整时间。并行车间所提供的M台机器属于非等同并行机，即同一种工件在不同的机器上的加工时间不一样。此外，加工每一种工件都需要在机器设备上安装与之对应的模具，且每种工件对应的模具数量一定，具体规则如下：

（1）在确定的生产周期内，所需加工工件的需求计划确定。

（2）每种工件对应的模具数量已知。

（3）每种工件在各个机器设备上的加工时间已知，不考虑移动时间。

（4）每种子批中仅有一种工件，并且具有不可拆分性，工件一旦开始加工就不能停止。

（5）每种工件具有一样的优先级，即没有优先或抢先生产的状况。

（6）同一时刻，每台机器仅有一个子批被加工，一个加工子批仅能在一台机器上进行加工；不同的工件在同一台机器上加工时，要考虑机器的调整时间，并且调整时间和工件的加工顺序相关。

（7）各台机器为不相关并行机，即相同工件在不同的机器上的加工时间不同。

（8）在加工之前所需加工工件的子批已在缓存区等待加工；所需加工的工件都已备好，并且所有机器设备上的第一个子批不需要调整。

本文选择合适的分批方案，以最小化最大完工时间为目标，建立以下数学模型[9-10]：

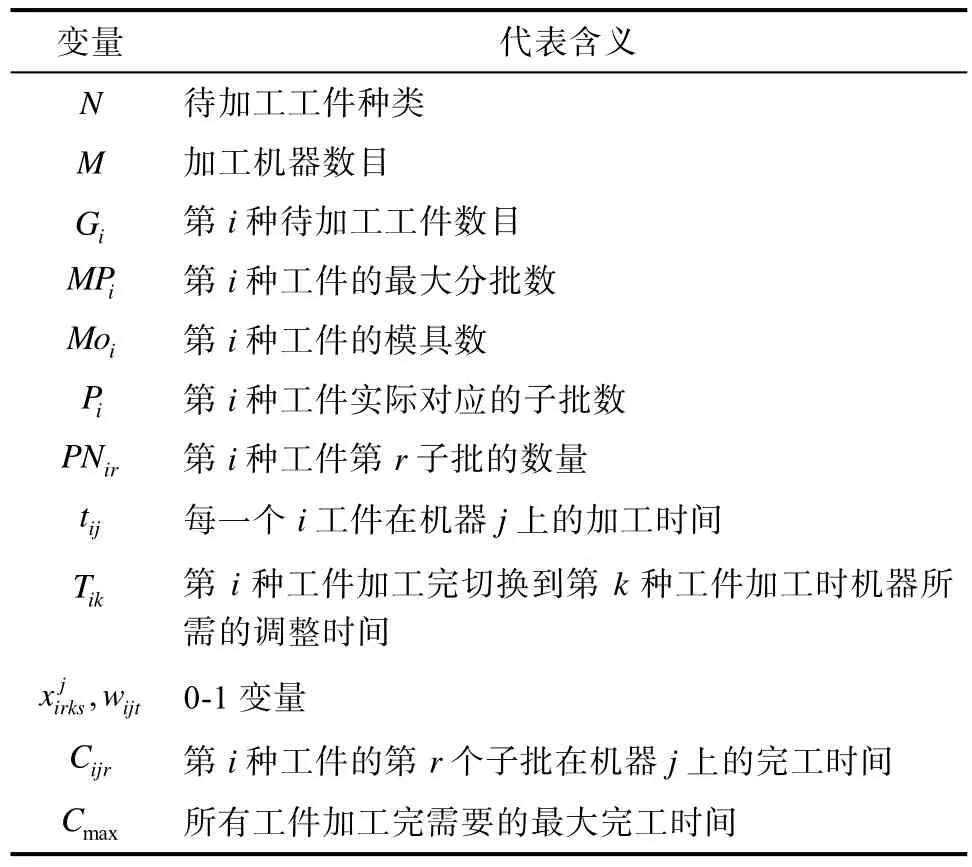
表1 各公式中变量和参数代表含义Tab.1 The meaning of variables

其中，公式（1）是为本文所研究问题的目标函数，在相关约束条件下，获得最小化最大完工时间；公式（2）确保每种工件的分批个数不大于工件的最大分批数；公式（3）、公式（4）、公式（5）为工件的分批策略，表示工件为均量分批。首先保证子批的数量一定为整数，然后对每种工件进行均量分批，最后还要确保所有子批的数量之和等于该工件的生产批量。其中[ ]为取整符号，取最为接近的整整；公式（6）、公式（7）分别表示每种子批在一台机器上进行加工时有且仅有一个紧前和紧后工件。公式（8）表明每个子批加工的优先级相同，且相邻的两个子批一定在同一台机器上进行加工。公式（9）、（10）用来求解每个子批的完工时间，了解各个子批完工时间之间的关系，且（10）表明工件每个子批的完工时间都大于等于 0。公式（11）代表求解最大完工时间。公式（12）表示任何一个时刻加工同种工件的最大子批数不大于其对应的模具数量；公式（13）表示0-1 变量。即其数值为1时，代表的意义分别为在t时刻，第i种工件在机器j上加工；第k种产品的第s子批在第i种工件的第r个子批加工完成后紧随进行加工，否则为0。

2 考虑机器调整时间的并行机分批调度问题算法求解

2.1 灰狼差分进化混合算法流程框架

对于并行机分批调度的研究，选用分批和子批的排序同时进行，选用灰狼差分进化混合算法求解考虑机器调整时间的并行机分批调度问题。其中，将最小化最大完工时间作为并行机分批调度问题的优化目标和验证算法寻优性能优劣的指标。现对算法流程进行简单的介绍，并给出算法流程图如图 1所示。

灰狼差分进化混合算法流程主要步骤如下：

步骤1：初始化种群。设定初始种群数量Np，最大迭代次数 Gmax,交叉概率 Pc。初始化种群初始迭代次数g = 0。

步骤 2：选取适应度函数并计算初始种群每个个体的适应度值Fi。保留该种群中的最优解。

步骤 3：种群更新迭代。通过灰狼差分进化混合算法更新机制对初始种群进行更新，得到新的测试种群。

步骤 4：非法种群个体修复操作。随着迭代次数的增加，测试种群中会出现一些不合理的个体，通过对其进行修复，得到新的种群。

图1 灰狼差分进化混合算法流程图Fig.1 Flowchart of grey wolf differential evolution hybrid algorithm

步骤 5：求解新种群中每一个个体的适应度值Fj，且保留当前种群中的最优值。

步骤6：比较Fi和Fj的大小，适应值大的个体留下，生成新的种群，并保留新种群中的最优解。

步骤7：令g = g + 1，判别是否达到终止条件，如果g≤maxG ，则转回步骤3继续进行迭代，直到满足条件；否则，迭代终止，输出最优值及对应的种群。

2.2 改进的灰狼差分进化混合算法设计

为了更好地提高问题的求解精度，实现工件分批和子批分配同时进行，在通过阅读相关文献进行比较后，本文选用文献所提出的三段染色体编码方式，设计了灰狼差分进化混合算法，并对该算法中灰狼算法的更新机制做出了相应的改动。

2.2.1 种群的编码和解码方式

基于并行机分批调度模型需考虑以下几个问题：如何对工件进行分批，工件分批后子批分别在那台机器上进行加工，同一台机器上各自子批的加工的顺序是怎样的。针对以上几个问题，本文设计了灰狼差分进化混合算法，编码方式具体注释如下：

将染色体分为三段，第一段P1P2…Pn代表的意思是：工件n分为几批，即子批的个数，它的长度和工件的种类数目一样，大小为N。第二段J11J12…JMP1…JMPn为符号编码，其代表的意义为：第n种工件的MPn个子批，如J11则代表第一个工件的第一个子批。但是，染色体的长度需要保持一致，因此子批的注明需要用工件的最大分批数来进行标注。例如工件A的分批数P1为2，但是其对应的最大分批数MP1为3，则代表着子批13的工件数量为0。第三段长度等于机器数目，MG1MG2…MGK则代表每台机器上所分批的子批数目。第一段和第三段的位置分别意味着相对应工件和机器。编码方式如图2所示。为了更方便的理解如何进行解码，现给出一个简单例子说明。假定工件种类有三种，且三种工件分别对应的模具数量为 2，3，3，每种工件待加工数量分别为 8，10，15，不考虑机器调整时间，现车间有三台可提供的加工机器，每台机器加工同种加工时间不同，即属于非等同并行机。如图 2.3所示，其代表一种可行的染色体。

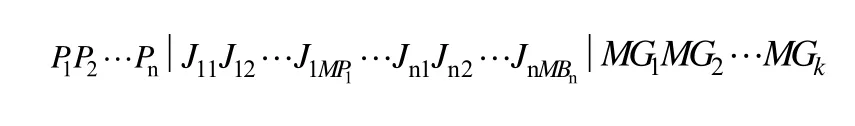
图2 灰狼差分进化混合算法编码方式Fig.2 Coding method of grey wolf differential evolution hybrid algorithm

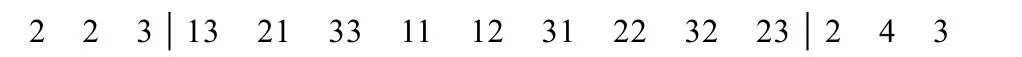
图3 一条可行的染色体Fig.3 A viable chromosome

该条染色体表示含义为：其中，染色体的第一段代表工件的分批个数，因此第一段的含义为三种工件分别分为2，2，3个子批进行生产加工。第二段代表的是每个子批如何分配，即每个子批具体分配到哪台机器上进行加工。如13则代表第一种工件第三批子批在第一台机器上加工。第三段的含义是三台机器分别需要加工的子批数量。2，4，3表示机器 M1，M2，M3分别需要加工的子批个数，且子批的加工顺序如染色体第二段所示。最终解码结果如表2所示。2.2.2 适应度函数

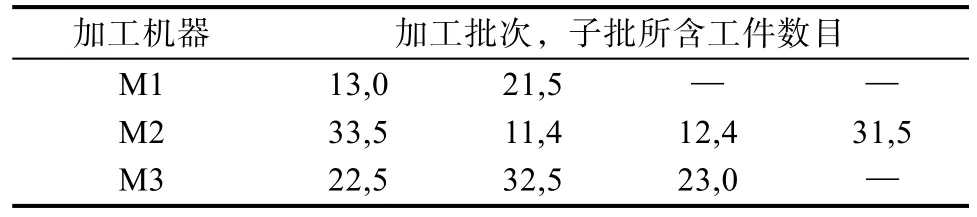
表2 解码结果Tab.2 The results of decoding

本文以最小化最大完工时间为优化目标，如公式（14）所示。适应度函数设为 F。需求适应度函数的最优解，适应度函数和优化目标关系为：

MinCmax作为灰狼差分进化混合算法的最优目标。

2.2.3 种群更新迭代方式

因为该染色体编码由实数编码和符号编码组成。故本文设计灰狼差分进化混合算法对模型求解。首先，染色体第一段和第三段为实数编码，故选取差分变异，交叉，选择操作；第二段染色体为符号编码，采用灰狼算法思想进行更新迭代。

（1）差分进化算法更新机制。对于差分变异，按照公式（15）和（16）对第一段和第三段染色体进行差分变异操作：

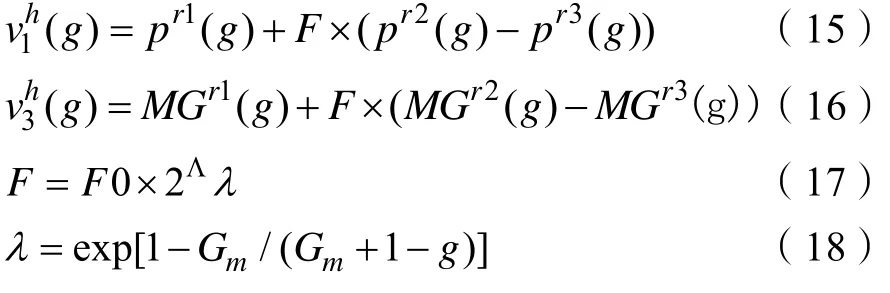
其中，差分变异操作的参数和变量含义如表 3所示。

表3 各参数和变量所代表含义Tab.3 The meaning of each parameter and variable

差分进化交叉操作选用二项式交叉，如方程（19）所示：

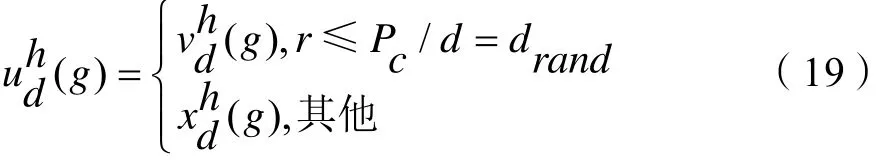
差分进化选择操作，对于算法迭代后产生的新个体需要与父代个体进行比较，适应度优的保留，适者生存，即择优筛选，优胜略汰，适应度值大的种群个体进入下一代种群中。其操作如公式（20）所示：

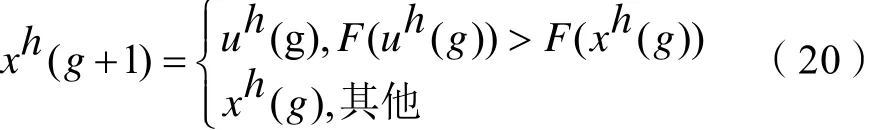
其中，差分进化交叉、选择操作参数和变量代表含义如表4所示。

表4 各参数和变量所代表含义Tab.4 The meaning of each parameter and variable

（2）改进的灰狼算法更新机制。第二段染色体所选算法为灰狼算法，现根据灰狼算法的基本思想对算法做如下改进：首先，参照反向学习思想，对初始种群进行优化，即先将初始种群扩大一倍，即先生成 2NP个个体对种群中每个个体的适应度值进行求解，选择所有适应度值较优的前NP个个体作为初始种群，这样可保证初始种群个体的优异性，提高解的质量。其次，因更新迭代皆是通过与三条最优染色体交叉变异而来，故会出现种群多样性不足的现象，并且随着迭代次数的不断累积，影响其收敛速率。针对这一问题，本文在灰狼算法中引入一个自适应因子，避免其陷入局部最优，防止早熟收敛状况。在得出三个最优解时，随机生成一个属于0到1的数字σ，比较其与a的大小，若其小于a,则其他染色体进行自身突变，否则与三条最优染色体进行交叉变异。即其他染色体以a的概率进行自身突变，以1-a的概率与最优染色体进行交叉变异。其表达式为：

最后，因为模型的调度目标是最小化最大完工时间，即所求的为头狼的位置，为增加其多样性，每次进行更新迭代后，在对最优解中的基因以 1/R的概率进行自身突变，引入变异算子如公式（22）所示：

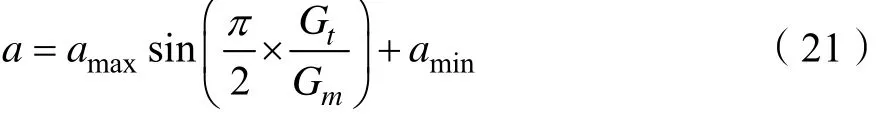
其中各参数和变量含义如下：vj和wj是xj取值的上下限，λ服从均匀分布，

2.2.4 非法个体修复操作

染色体第一段和第三段为实数编码，第一段为工件分批数，其数值小于等于模具数，第三段为机器所分到的子批个数，其数值总和为每种工件的模具数量之和。而随着算法的不断迭代，染色体第一段和第三段的数值将会发生改变，相应染色体可能会产生不合规则的基因，因此设置以下规则：若第一段基因数值小于0，则规定其数值为1；若使其数值大于该工件的模具数Mo，则规定其数值为Mo。对于第三段染色体做以下规定，每次迭代更新后，第三段染色体基因数值进行归元化处理，使即重新选择第三段基因，为使每台机器都在加工，不会存在空余机台，浪费资源，因此当染色体第三段上基因值小于0时，对其进行订正操作，使其数值为1。

3 仿真实验

考虑机器调整时间的并行机分批调度实例问题和算法参数的设置如下：在该实例中，待加工工件种类为10，每种工件数量分别为：200，300，500，300，400，300，500，400，200，400。加工时间如表5所示。

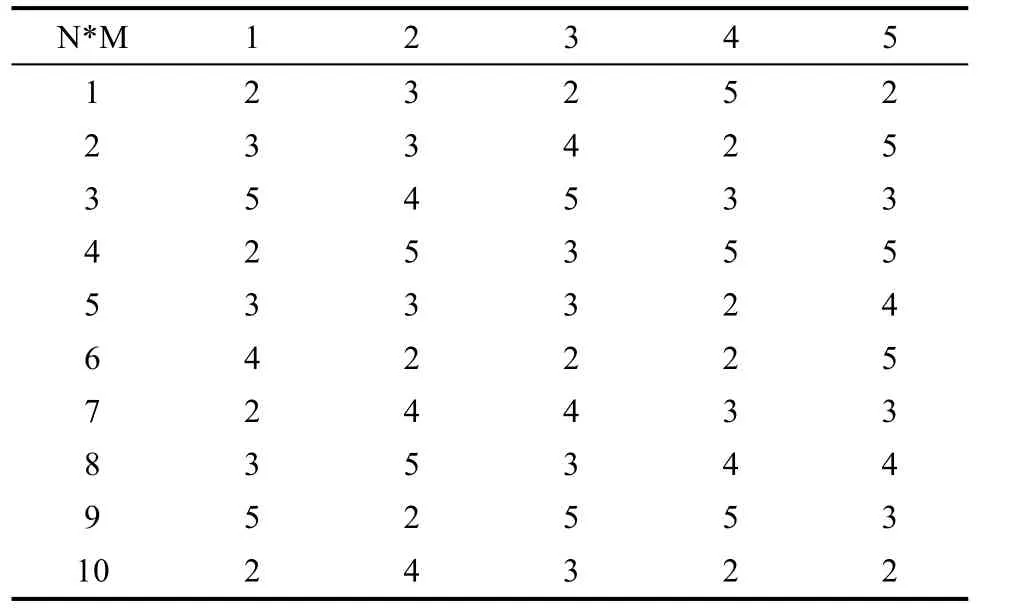
表5 单个工件在机器上的加工时间Tab.5 Processing Time of Single Workpiece on Machine

不同工件在同一台机器上进行加工时，需要考虑工件在机器上的调整时间，且每一种工件在不同的机台上对应的调整时间也不尽相同，工件在机器上的调整时间如表6所示。

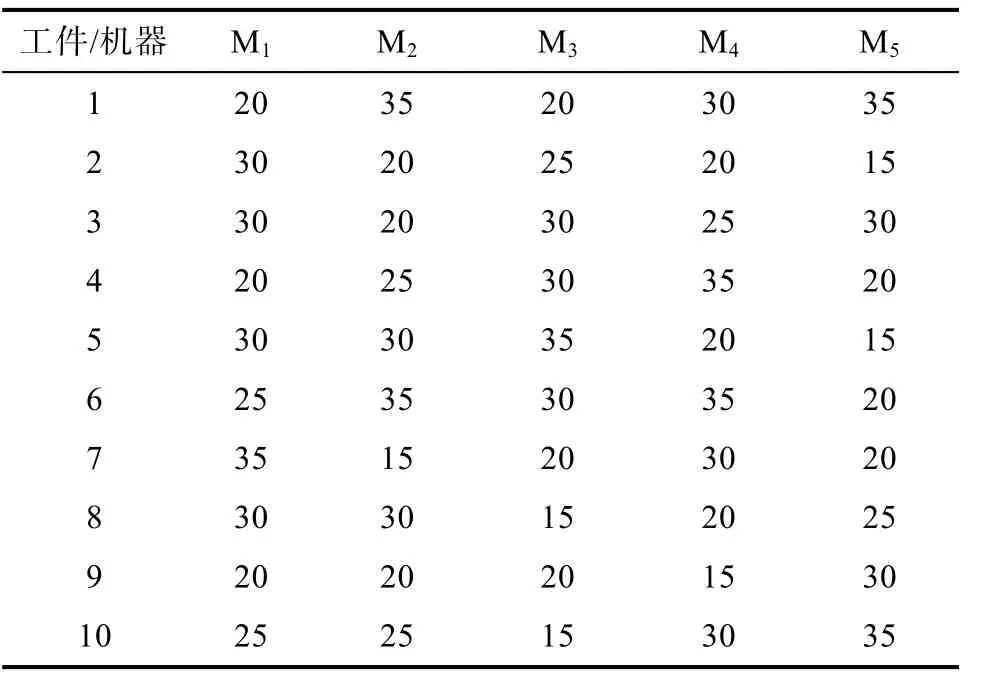
表6 同一台机器加工不同产品需要的调整时间Tab.6 Adjustment time needed for processing different products on the same machine

该实例分别采用灰狼差分进化混合算法和遗传差分进化混合算法进行求解。其中两种算法的参数设置如下：种群数量N为20，最大迭代次数Gm为200，交叉PC为0.5，交叉算子F0为0.8。模型仿真优化系统的运行环境为：Inter Core i7-7700HQ CPU 2.80 GHz，8.00 GB内存，64位win10操作系统。

4 算例结果分析

将两种算法分别在考虑机器调整时间的并行机分批调度模型中独立运行10次，灰狼差分进化混合算法和遗传差分进化混合算法在 10次搜索中得到的最优解如表7所示。

表7 10次运行寻优结果统计表Tab.7 Statistical results table of 10 times optimization

由表7可以看出，所有的JV数值皆大于零，这表明在考虑机器调整时间的并行机分批问题的求解中，灰狼差分进化混合算法在每次独立运行时得到的近似最优解的精度要高于遗传差分进化混合算法搜寻得到的近似最优解。为方便观察，现展现该实例问题通过两种算法求解独立运行 10次的迭代收敛图如图4所示。

从两种算法十次寻优的迭代收敛图中可以看出，灰狼差分进化混合算法的寻优性能要优于遗传差分进化混合算法。其中，算法在第2次、第3次和第7次独立运行时，迭代初期遗传差分进化混合算法所搜索到的目标函数值比灰狼差分进化混合算法搜索的优解要好，但是随着迭代次数的增加，灰狼差分进化混合算法在寻优性能上的优势逐渐体现出来，从图4（2）、图4（3）和图4（7）中可以看出，在搜索后期，灰狼差分进化混合算法的寻优性能明显高于遗传差分进化混合算法。另外在第8次和第9次的迭代收敛图中，本文所设计算法在一开始的收敛性能就优于遗传差分进化混合算法，随后在整个迭代过程中所得到的最优解也优于对比算法，证明了所设计算法的优越性。综合这十次的寻优迭代收敛图来说，灰狼差分进化混合算法在求解考虑调整时间的并行机分批调度问题上具有较高的收敛性能，且相较于遗传差分进化混合算法，其寻优性能更佳。为了更为直观的表述两种算法在求解过程中所获得的最优解的差异，现对两种算法针对10*5规模的考虑调整时间的并行机分批调度在 10次独立运行中所获得的最优解值进行比较，并给出10次独立运行中所搜寻到最优解的迭代收敛图，分别如图5所示。

从图5可以明确看出，在10次求解过程中，灰狼差分进化混合算法所搜索到的最优解明显优于遗传差分进化混合算法所搜寻到的最优值，在十次独立运行中，灰狼差分进化混合算法所求的最优值1728 min，相较于遗传差分进化混合算法所求的最优值完工时间缩短了184 min，证明了灰狼差分混合算法比遗传差分进化混合算法的寻优性能更佳。现针对两种算法在求解的稳定性和寻优性能等方面进行对比，对比结果如表8所示。

图4 10＊5规模问题独立运行10次的迭代收敛图Fig.4 Convergence diagram of 10＊5 scale independent operation for 10 times

图5 最优解迭代图Fig.5 Optimal iteration graph

表8中，MinCmax代表最小化最大完工时间，即算法优化的最终目标。其单位为 min。Avg表示两种算法独立运行二十次所得到的最优解的均值。单位为min。SD为两种算法独立运行10次得到的最优解的标准差，反映最优目标的离散程度，即算法本身求解的稳定性。灰狼差分进化混合算法搜寻得到的最优值均值为1982.2 min，而遗传差分进化混合算法得到的最优解均值为 2119.8 min，其搜索的完工时间大于灰狼差分进化混合算法，且两种算法在10次独立运行中所搜寻的最优解相差184 min。由此可见，本文所采用的灰狼差分进化算法在寻优精度上明显优于遗传差分进化算法。但是在寻优稳定性上，灰狼差分进化混合算法的标准差为87.41，遗传差分进化混合算法的标准差为68.95，灰狼差分进化混合算法相比于遗传差分进化混合算法所搜索到的最优目标函数值的离散程度大，表明了本文所设计的算法极大的改善了算法寻优性能。