质量管理体系过程确认中实验设计案例的研究

◆俞钟行 / 文

原例解读

GHTF（Global Harmonization Task Force）的“质量管理体系-过程确认指南”（第2版）[1]里，有个用热封机对无菌隔离袋封装的案例。指标为密封强度，规定在2～4kg，目标值是3kg,过程能力Cpk必须大于1。因素有4个，水平值见表1。

要注意：表中B、C和D三个因素是可控因素，A是误差因素。作全析因试验，试验次数为54次，每次计算10个袋子的密封强度，表2给出试验方案和结果。y是平均值，z是6倍标准差（6σ）。原文第33～37次试验（共5次）是缺失的。

从结果可以明显看出，当处于150℃时密封强度是不可接受的（总平均值为2.38kg，6σ=1.42）。而在规定范围内的时间和压力变化，对密封强度没有造成什么影响。

于是把最低温度提至155℃，时间和压力变化与前类似，又进行36次试验，总平均=2.92kg, 6σ=0.5，Cp=1.8。得该热封机最佳设置为时间1.5s，压力325kPa；原文未提温度，可以推测温度为（155+170）/2=162.5℃。

表1 因素水平表

然后在正常生产过程中封装袋子，热封机设置分别为（1）最佳设置；（2）低温、低压和短时间；

（3）高温、高压和长时间。在每个设置组合下分别产出了190个产品。（1）～（3）的平均值和6σ结果分别是：3.08、0.3；2.8、0.5；2.9、0.6。所画控制图无异常，整个过程产生的Cpk=1.75，过程被证明是有能力的。

以上过程确认的DOE，未利用很多有效的统计分析手段，耗费54×10+3×190=1110个袋子。

表2 试验方案和结果

对原例数据的统计分析

用excel的SUMIF等函数对表2作极差分析，得表3。因为因素A是2水平，其余是3水平，比较各因素强弱时应当使用折合系数（略）。但容易看出无论y或z，因素C“温度”都是最强的因素。

还可以画出相应的因素趋势图1。

为了达到目标值=3kg且Cpk大于1，必须找到因素的最佳组合，使指标平均值接近3且6倍标准差（6σ）足够小。对表2最右两列数据y、z画散点图（图2），可以看出6σ与平均值呈负相关，且若平均值y接近3，则6σ比较小。因此只要做到指标y接近3，Cpk大于1的目标基本也就达到了。

故用excel“数据分析”中的“回归”对指标y作分析，结果见图3。

仅从图3的“方差分析”中残差SS/总计

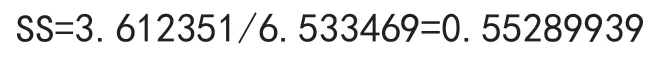
来看，回归方程严重失拟，此值在工程上一般要求处在5%～10%之间。

但在y的因素趋势图-图1（a）中，因素C最强且略呈V状（角状），根据经验可能是2次项；因素B与C走势交叉，可能有交互作用。于是如表4所示，在表2中进行“插项”。如表4中C C 就是C 的2 次方，如22500=1502。

表3 极差分析

图1 全析因试验的因素趋势图

然后再用excel的“回归”模块对y分析。限于篇幅，未给如图3回归结果。但表5列出全析因试验“插项”前后回归结果中的各重要参数。其中Ru是比较不同回归方程优劣的，计算公式为Ru=1-（1-R）（n+k+1）/(n-k-1)[2]。

式中，R：多重相关系数；n：数据个数；k：excel回归分析的“回归自由度”即“因素个数”。最优者是当Ru是正数且数值最大时的回归方程。举例来说，表2的方程的Ru=1-(1-.668656)(49+4+1)/(49-4-1)=0.59335。

从表5看出，通过2次插项，回归结果的复相关系数Multiple R和Ru都明显上升；标准误差、Significance F（即p值）、残差SS/总计SS、因素ABC的p值都明显下降，且达到显著水平；2次插入的因素也达到显著的水平。这都表明回归的拟合优度已得到大幅度的提升。但本来就是最弱因素D的p值仍很大甚至更差，最终的残差SS/总计SS=0.198仍偏大，姑且告一段落。

可以从类似于图3 的Coefficients（系数）列里得到回归方程如下：

Y=-114.347+0.058116A+5.258664B+1.390661C+0.000105D-0.0041CC-0.03313BC

然后用excel的“规划求解”模块对方程选优。设目标值=3.0；4个因素各有两个约束条件见表1，最好对于因素A加一个“整数”的约束条件。得到初始条件为0时的一个局部选优的解如表6。注意A不是可控因素，而是误差因素，故试以A=-1代入表6时，y=2.788，情况稍差些。再来计算6σ。注意到y是10个袋子强度平均值及标准误差为0.175673（表5），6σ=（0.175673/101/2）х6=0.333。因此过程能力Cpk是充裕的。这里的统计分析在一定程度上可取代前文三种设置下各生产190个产品的试验。

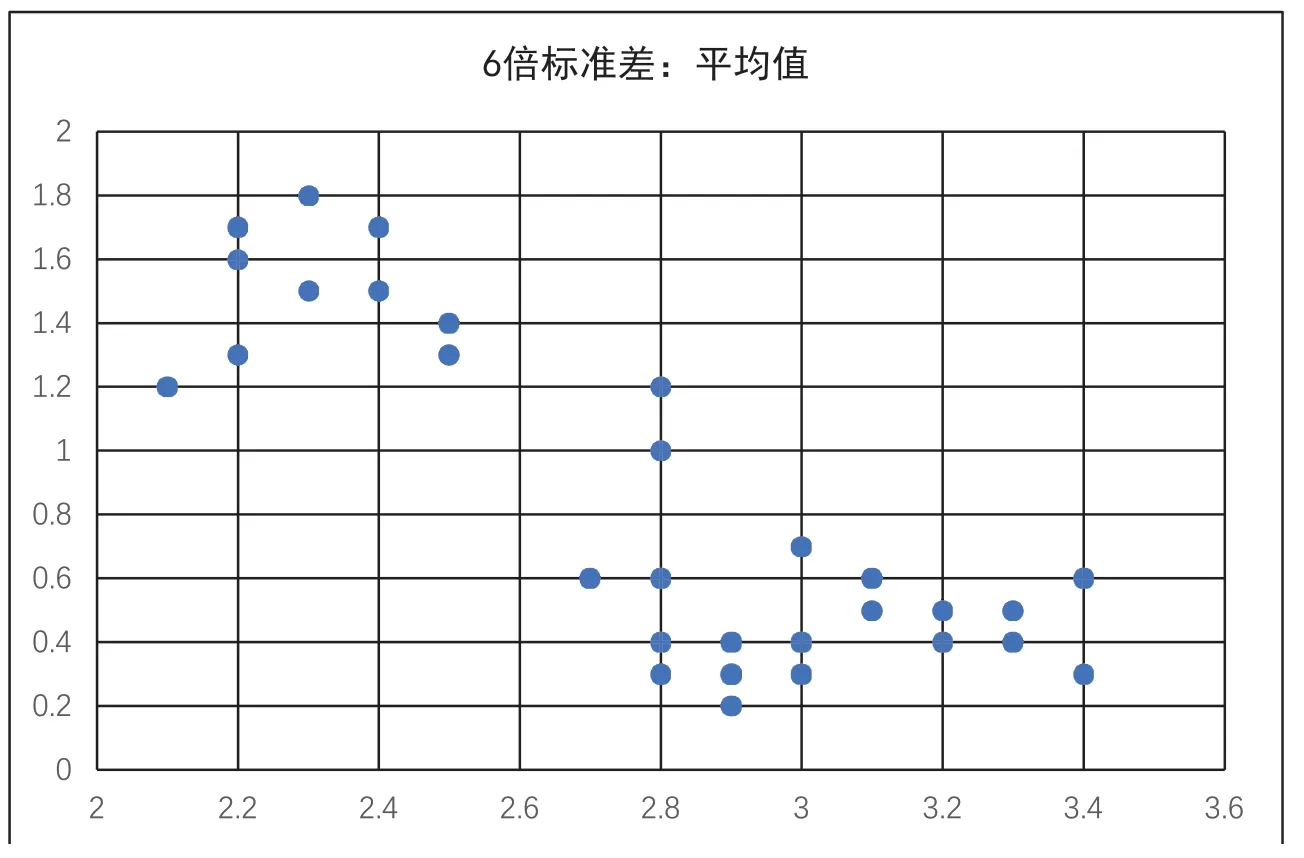
图2 全析因试验的6σ对平均值的散点图

图3 全析因试验的回归分析结果

表4 在excel电子表格里插项

以L9（34）来完成过程确认的试验

在表2中挑出符合L9（34）的9次试验，并作y平均极差分析，画出因素趋势图，见表7与图4。因为原全析因试验缺少5次试验数据，L9（34）的第6 次试验 恰巧也缺失。但发现全析因试验的第51、15次试验的A、B、C都与L9（34）的第6次相同，只是D不同；且第51、15次试验的D分别是350和300，y平均都是2.7，则判断L9（34）的第6次的D在325情况下，y平均也应是2.7。另外因素A是2水平，故在L9（34）中作了拟水平的处理。可以看出y平均的极差分析得到的因素从强至弱的排序C、A、B、D，以及因素趋势图的形状都类似于原全析因试验。

类似于全析因试验情况下，插入CC和BC项后再回归，得图5所示结果。总的来说得到了拟合优度不错的回归方程，且各重要参数与全析因的表5最右列相仿（如4个因素和2个插入项的p值大小排序）。

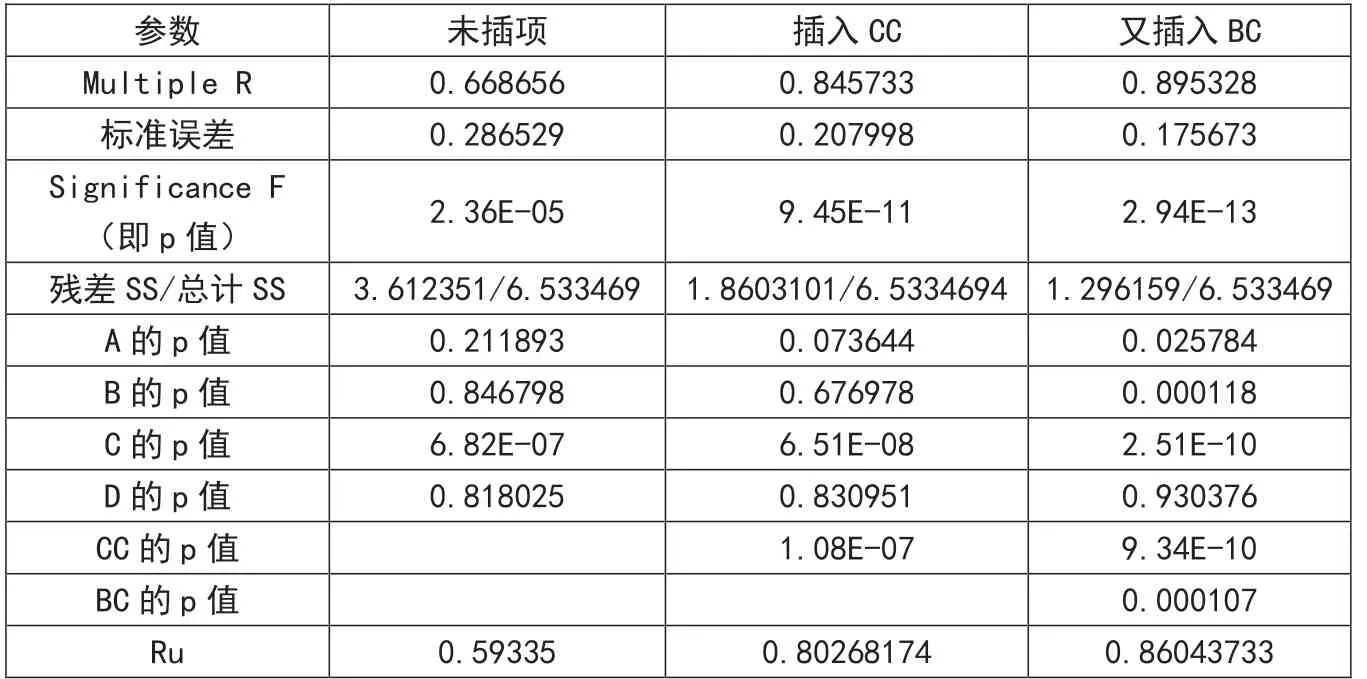
表5 全析因试验“插项”前后回归结果中的各重要参数

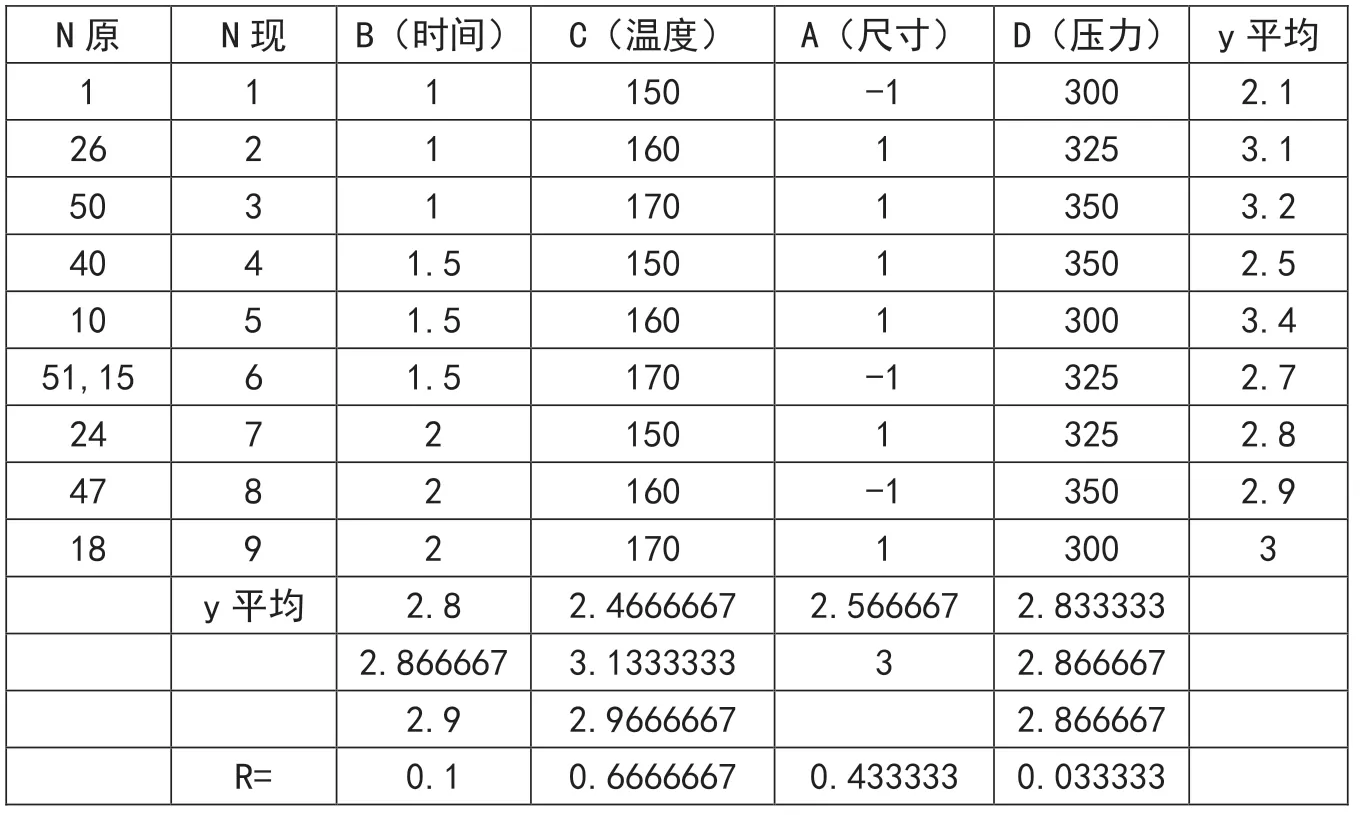
表7 L9（34）试验与极差分析

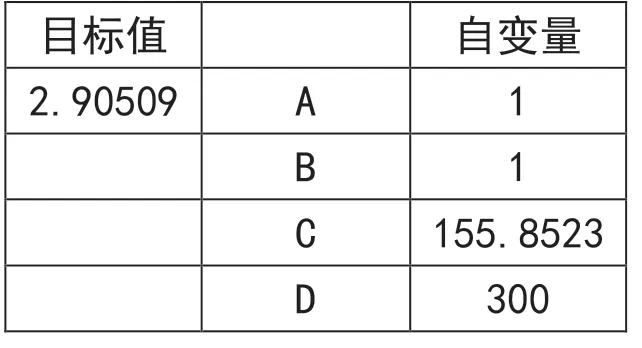
表6 规划求解的结果

图4 L9（34）的因素趋势图

最后以Coefficients（系数）列里显示的回归方程，用规划求解选优。得到初始条件为0时的局部最优组合如表8所示。虽然在全析因试验时曾得到“当处于150℃时密封强度是不可接受的”的结论，但仔细查看原始数据，虽然温度C=150℃，但若时间B=2s、尺寸A=1（大尺寸），则y平均与6σ也都是不错的，正如表8所示的结果。因为因素A是误差因素，再将A=-1代入表8，得y=2.670。由于标准误差为0.102402，故Cpk也都是足够的。但也可以改变初始条件多作几次规划求解，以选得最优组合。

图5 L9（34）试验插项后的回归结果

讨论：如果按照田口方法的思路，把可控因素B、C、D用L9（34）来安排试验，把A作为误差因素以“外表”作2次情况，则一共作18次试验。这样既可避免“拟水平”造成的误差，也仍可以用前述的以excel作“回归”和“规划求解”的手法。另外，如果本例的y平均与标准差不是如图2所示的负相关情况，则必须考虑2个指标的问题，且1个指标是望目、另1个指标是望小。这时或许要用运筹学里“多目标决策”的“功效系数法-几何平均法”。

表8 L9（34）的规划求解结果