寻找囚禁在光腔中的玻色-爱因斯坦凝聚体的八重准晶

余炎强, 郑东琛, 叶春荣, 廖任远

(1.福建师范大学 物理与能源学院 福建省量子调控与新能源材料重点实验室，福州 350117； 2.福建省半导体光电材料及其高效转换器件协同创新中心，厦门 361005)

1 引 言

准晶是一种介于晶体和非晶体之间的物质，它具有像晶体一样的长程有序的原子排列，但是却没有像晶体一样的平移不变性.人们已经在合金[1], 胶体[2]中观察到了准晶.而通过衍射图像观察到准晶具有旋转对称性则要追溯到1984年[3].准晶序已经在很多材料中被研究和学习[4-6].

将超冷原子囚禁在由激光产生的光学势中可以很好地调控和探索奇特的固态物质.许多研究小组利用这样的装置成功探索了超流气体的Dicke量子相变[7,8]；在两个腔中实现了超固态；希格斯模和戈德斯通模[9-11]；将一个三维的凝聚体放置在一个拥有五个势阱的一维超晶格中实现了具有五重旋转对称性的准晶[12]，还有的方案是通过自旋轨道耦合的BEC经过量子相变产生准晶[13].最近来自英国的研究小组将BEC放入到光学腔中，通过观察产生的衍射图像实现了八重准晶[14].但是对于该装置还缺少必要的理论解释来证明实验的准确性以及该实验装置的可重复性.所以本文将利用数值模拟从理论上证实光学腔中出现的八重准晶.我们将会结合虚时演化和分步傅里叶方法来计算不同腔模情况下的原子密度分布情况.我们从理论上证实了当四个线性腔同时作用于BEC时会出现具有八重旋转对称性的准晶.所以这篇文章再一次证明了光学腔中的BEC可以产生很多奇特的量子现象.而利用我们的理论方法可以很好地模拟实验所观测到的现象，这为我们之后探究更为复杂的晶体结构提供了理论基础.

2 模型与方法

考虑将超冷玻色气体囚禁在一个由四个线性腔组成的二维x-y平面上并在z方向上受到一个泵浦激光的作用，每个腔之间的夹角为45°[15]，如图1所示.我们将原子的失谐量定义为Δa=ωp-ωa<0，其中ωp表示泵浦频率，ωa表示原子基态和激发态之间的转变频率，假设ωa的取值非常大，所以原子的激发态可以被绝热消除.这就产生了该模型的有效哈密顿量.

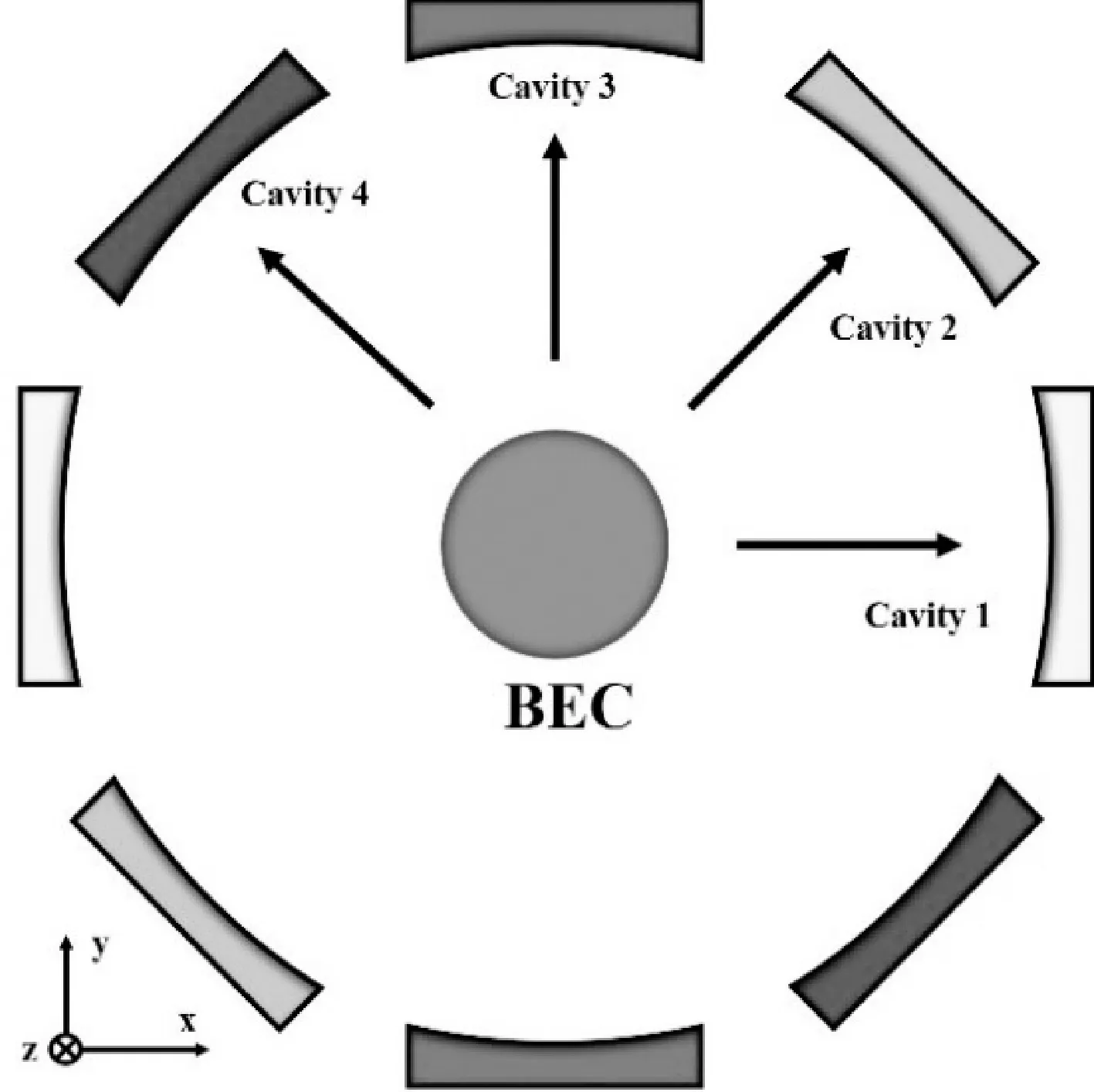
图1 模型图Fig.1 Illustration of model

(1)

(2)

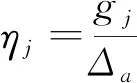
(3)

(4)

(5)

从上式可以知道分步傅里叶方法要求时间取得小一些，而虚时演化又需要时间取得大一些，解决的途径是将时间步长取小，这样我们就可以结合两种方法快速准确地得到基态波函数.

3 结果与讨论

第二部分通过引入四个线性腔中的哈密顿量，利用一些近似得到有效哈密顿量，最后结合虚时演化方法和分步傅里叶方法得到该哈密顿量的基态波函数.现在可以根据求得的基态波函数画出腔内原子密度分布图.如图2所示，我们根据数值模拟方法得到了光学腔中的原子密度分布，只考虑一个腔沿x轴作用时，得到图2a所示情况，它表示沿x方向出现原子密度分布，这对应于只有腔1中出现超辐射相.接着我们考虑加入竖直方向的晶格势，也就是加入图1所示的腔3，通过模拟可以得到规则分布的二维菱形晶格.如图2b所示，它表示腔1和腔3中都出现超辐射相.最后加入腔2和腔4的晶格势，我们得到一个二维晶体结构，它是一个具有八重旋转对称性的晶体，相比于图2c，图2d中作用于凝聚体的激光强度更大.

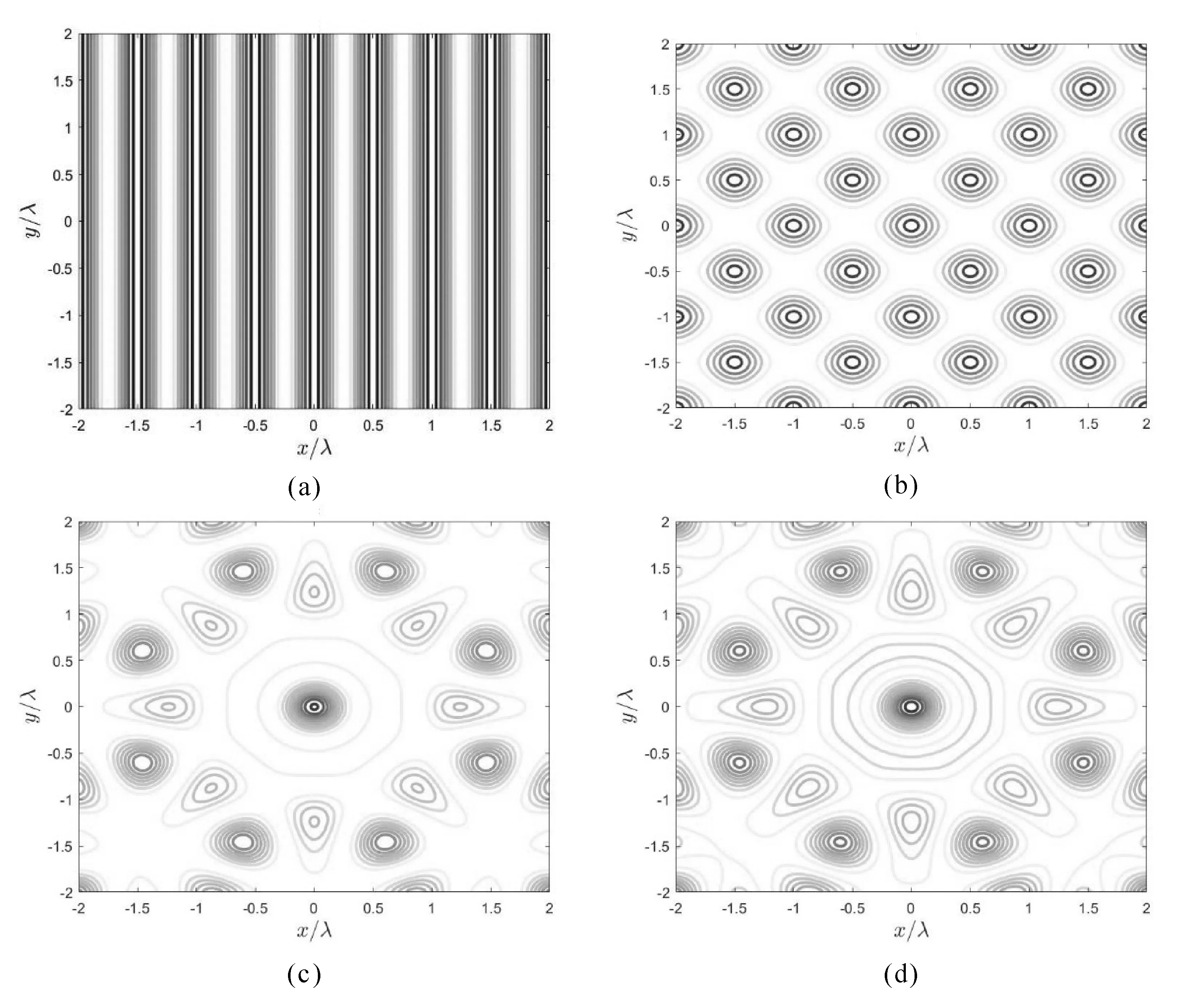
(a;b;d:ηj=0.5,c:ηj=0.05)图2 不同腔晶格势作用下的原子密度分布Fig.2 Atomic density distribution under different cavity lattice potentials

接着我们进一步探索八个周期时的情况，所采用的方法与图2类似，经过数值模拟我们得到了图3所示的情况.从图中我们可以看到这个晶体结构具有长程序，但不具有平移不变性.所以根据准晶的定义，该晶体是一个八重准晶.

(a:ηj=0.5)图3 八个周期下的原子密度分布Fig.3 Atomic density distribution at eight cycles

4 总 结

本文建立了一个由四个光学腔组成的系统，并将超冷玻色气体囚禁在腔中.为了探究腔中出现的相图，并且解释实验出现的现象，我们通过结合虚时演化方法和分步傅里叶方法来求解GP方程，该方法能够有效解决非线性薛定谔方程.通过改变不同数目的腔晶格势，得到了相应的相图.当所有腔都考虑在内时，出现一种具有八重旋转对称性的晶体，该晶体具有长程序但不具有周期性，所以它是一种八重准晶.这说明了我们的方法适用于研究光学腔中的晶体结构和相变.近几年实验上观测到的Dicke量子相变可以通过单个线性腔来实现，而利用我们的数值模拟方法也能够从理论上得出相对应的相图，而利用两个交叉腔可以模拟超固态的产生，利用三个腔可以产生六角蜂窝状晶格.本文利用四个呈45°分布的光学腔成功模拟出八重准晶.所以我们的方法是十分科学有效的，它为将来探究更为复杂的晶体结构提供了可能，并能够进一步指导实验的操作.