Ab initio calculations of structural evolution and conductance of binary compound GaN chain on gold leads
2020-05-15JIAXiaoMUYiCHANGJingZHANGTianZHOUXiaoLin
JIA Xiao, MU Yi, CHANG Jing, ZHANG Tian, ZHOU Xiao-Lin
(College of Physics and Electronic Engineering, Sichuan Normal University, Chengdu 610101, China)
Abstract: By performing Ab inito density functional theory plus the non-equilibrium Green’s function method, we investigate the electron transport properties of binary GaN molecular chain sandwiched between the Au electrodes for the first time.We simulate the Au-(GaN)2-Au junctions breaking process, calculate the corresponding cohesion energy, obtain the equilibrium conductance and the projected density of states of junctions in the optimal position.In additional, both the current and conductance of junctions at the optimal position are computed under small bias.It is found that, with the increase of the bias voltage, the conductance of the GaN molecular chain always decreases.The I-V curve displays a non-linear relationship, indicating that the junctions have a semiconductor-like characteristic.
Key words: Density functional theory; Non-equilibrium Green’s function; Electron transport properties; Projected density of states; I-V curve
1 Introduction
As we known, the energy spectrum of the molecule is quantized.Most of these materials show unusual results as soon as the diameters of the contacts are reduced.Due to the quantum nature of the electrons, the transport properties are determined by quantum effect.Using techniques such as scanning tunneling microcopy, mechanically controllable break junctions formed by mechanical strain, or electromigration, the transport properties of nanosized junctions were intensively studied.These techniques allow for forming atomic-sized contacts or for trapping molecules.The study of transport trough single-atomic contacts[1-3]and molecules[4-6]are of great fundamental interest since they might be applicable in future electronic and energy-conversion devices based on electron transfer, shot noise, heat transport, negative differential resistance, and gate-controlled effects[6-16].
Molecular chains have received intensive investigations both theoretically and experimentally.In experiment,Lafferentzetal[5], measured the conductance and mechanical characteristics of a single polyfluoreme wire by pulling it up from an Au (1 1 1) surface with the tip of a scanning tunneling.In theoretical, Maslyuketal[4], using theabinitionon-equilibrium Green’s-function formalism, investigated the transport properties of the organometallic vanadium-benzene molecules sandwiched between magnetic Co (1 0 0) electrodes, and found that the zero bias conductance of the majority electrons is small and decays exponentially with increasing length of the molecule, and the minority electrons are responsible for the oscillatory character of the transmission.Such results are very similar to the even-odd oscillation in metallic junctions[17].There is intense interest in the development of semiconductor nanowire device structures[18,19], especially for Group III nitride.Group Ⅲ nitride semiconductors own generally large direct electronic band gap, and high chemical stability and excellent physical properties, including high saturated electron drift velocity, high breakdown voltage, high heat conductivity and so on.These superior performances inspire people to examining the transport properties of Group III nitride based nanowires for possible application in low-power and high-density field-effect transistors (FETs), solar cells, terahertz emitters, and detectors.Hence, in this paper, we will investigate the transport properties, and examine the conductance of the binary compound GaN molecular chains attached to Au leads using the density functional theory combined with the non-equilibrium Green’s function method.The rest of the paper is organized as follows: The theoretical methods and the computational details are given in Section 2.Some results and discussion are presented in Section 3.Finally, the summary of our main results is given in Section 4.
2 Theoretical mode and calculation details
Our theoretical investigations for the electronic transport properties of the system are based on theabinitiodensity functional theory (DFT) as implemented in the Siesta code[20]and the non-equilibrium Green’s function (NEGF) approach realized in the Smeagol[21-23].The structural model for our theoretical analysis is illustrated in Fig.1.In this two-probe system, a GaN molecular chain couples with two atomic scale Au (1 0 0) electrodes which extend to reservoirs at ± ∞ where the current is collected.Two Au atomic layers have been chosen for the electrode cell in thezdirection, and a large enough vacuum layer is included in the electrode cell in thexandydirection so that the device has no interaction with its mirror images.In the central scattering region, the GaN molecular chain couples with seven atomic layers to the left electrode and with six atomic layers to the right electrode.These atomic layers in the central scattering region are large enough[24]so that the perturbation effect from the scattering region is screened and they are denoted as surface-atomic layers.
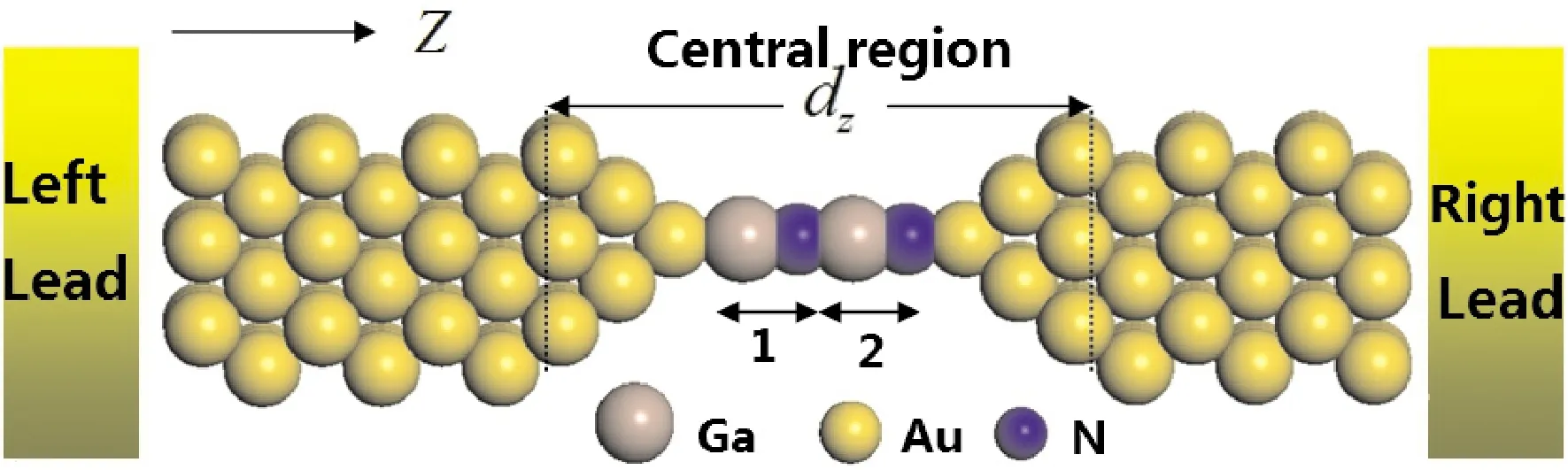
Fig.1 Model used for the calculation of the GaN chain connecting (1 0 0) oriented fcc Au leads.
This simulation procedure of such two-probe systems can be described briefly as follows: Firstly, the electronic structure of two electrodes is calculated only once by Smeagol to get a self-consistent potential.This potential will be shifted rigidly relative to each other by the external potential bias and provided the natural real space boundary conditions for the Kohn-Sham (KS) effective potential of the central scattering region.Then from the Green’s function of the central scattering region, we can obtain the density matrix and thereby the electron density.Once the electron density is known, the DFT Hamiltonian matrix, which is used to evaluate the Green’s function, can be computed using the above boundary conditions by means of standard methods.The central quantity of the method is the retarded Green’s function of the entire system, which is defined by direct inversion of the equation:
(ε+S-H)GR(E)=I,
(1)
ε+=limδ→0+E+iδ,
(2)
whereHis the Hamiltonian matrix,Sis the corresponding overlap matrix,Iis an infinite-dimensional identity matrix, andEis the energy.Because the interaction of the GaN molecular chain with electrodes can be incorporated into the self-energy ΣL/R(E).we can focus our attention on the calculation of the retarded Green’s function of the scattering region
(3)
More calculation details on how this procedure is performed in Smeagol can be found in theliterature[23, 25].To calculate the most stable structure of the Au-(GaN)2-Au contacts, we perform geometry relaxation by keeping all gold atoms in the leads fixed and relaxing the apexes of the point contact in the center until the force on each atom is smaller than 0.1 eV/ Å in the optimization[26].The ground state energy is therefore calculated as a function of the distancedzbetween the outer slices, i.e.we simulate a junction breaking process.The experimental lattice constant of gold, a=4.078 Å, is used for the electrodes[27].
In our calculations, we use the Perdew-Zunger form[28]of the local-density approximation to the exchange-correlation functional.Nonlocal scalar-relativistic Troullier-Martins pseudo-potentials are generated from the configurations: Au (5d106s1), Ga (4s24p1) and N (2s22p3).A single-zeta is used as the basis set for Au, whereas a double-zeta basis is adopted for the orbitals of the other species (Ga and N).A periodic boundary condition is applied in the basal plane (orthogonal to the transport direction) with four irreducible k-points in the two-dimensional Brillouin zone.The Brillouin zone is set to be 2×2×100 points following the Monkhorst-Pack k-point scheme[29].The cut-off energy and iterated convergence criterion for total energy are set to 200 Rydberg and 10-4, respectively.Furthermore, the charge density is integrated over 50 energy points along the semi-circle, 20 energy points along the line in the complex plane and 20 poles are used for the Fermi distribution.
3 Results and discussion
As we known, it is difficult to precisely measure and control the separation between the tip and the surface in STMexperiments[30]or the molecule-metal separation in the mechanically controllable break-junction (MCB) experiments.Especially in the MCB experiments, the molecule is probably lengthened or compressed from the metal and may not locate in its equilibrium position[31].Hence, in order to calculate the most stable structures for the GaN molecular chain attached to leads in different distances, we calculate the cohesion energy as a function ofdzduring the simulation process.The cohesion energy is defined as follows: △E=E(Au electrodes + GaN molecular chain) -E(GaN molecular chain)-E(Au electrodes).The calculated results are shown in Fig.2 (marked in solid pink squares and right-hand side axis).
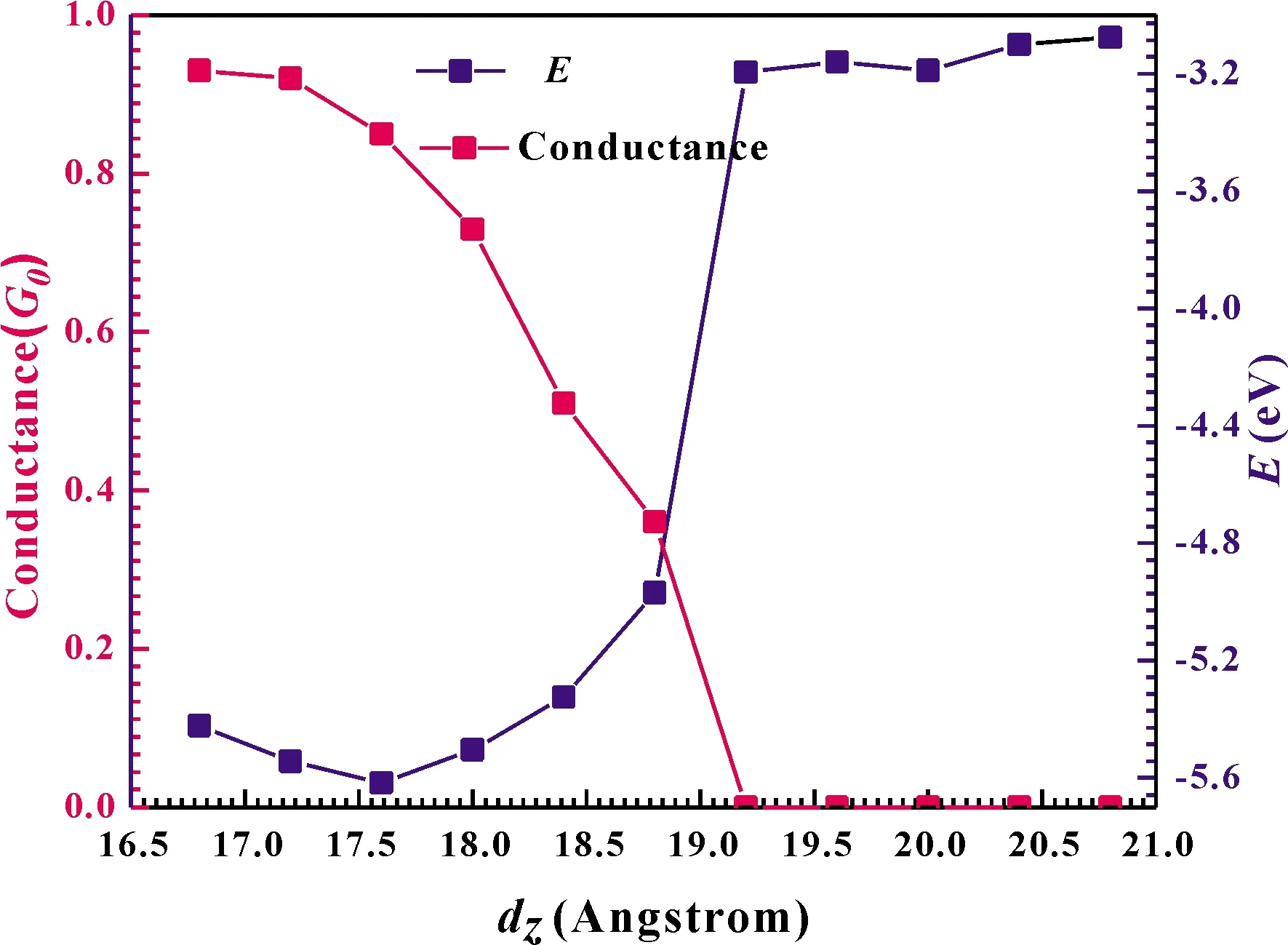
Fig.2 Conductance (pink squares and left-hand side axis) and the cohesion energy (blue squares and right-hand side axis) as a function of distance dz.
we can find that after relaxation, all the Au-(GaN)2-Au junctions remain straight, i.e.the GaN molecules align perfectly.From this figure we can see that, there is an obvious parabola in the curve of the total energy as a function ofdzfor the GaN molecular chain.The distancedz,eqcorresponding to those energy minima describes the equilibrium position, which is the system that will naturally form if the electrodes are free to relax.It can be found that, in the range from 16.8 Å to 18.8 Å, there is a minimum value of the cohesion energy.The minimum energy in the curve is located at the equilibrium distance,dz,eq= 17.6 Å.When the junctions are the optimal equilibrium position, the Ga-N bond-length is 1.871 Å, which is well consistent with other theoretical results[32-34].Additionally, during the simulations, we calculate the conductance as a function of distancedz, which is shown in Fig.2 (marked in solid blue squares and left-hand side axis).This conductanceGassociated to the two-probe device can be calculated by using Fisher-Lee’s relation[35]
(4)
where the ГL/Ris the anti-Hermitian part of the self-energy,eis the electron charge, andhis the Planck’s constant.T(E) is the simple energy-dependent total transmission coefficient of standard scattering theory[36].We can clearly find that the conductance changes significantly with thedz, demonstrating that the conductance of junction is sensitive to the variation of the two-contact distance and anchoring geometries, in other words, high sensitivity of the conductance to the local atomic re-arrangement of the contact region[37].For more details, the conductance changes from 0.93G0(G0= 2e2/his the conductance quantum) atdz~ 16.8 Å to 0.36G0atdz~ 18.8 Å with the junctions stretched, and then atdz= 19.2 Å, its conductance jumps abruptly to 0, where is the N-Au bond breaks point.From the Fig.2, we can see that, when the distancedzis larger than the value of 19.2 Å, almost no electron can tunnel from one electrode to the other.Additionally, it can be found that the equilibrium conductance of the GaN chain is 0.85G0which is not the largest in the range of 16.8 Å to 20.8 Å.In fact, the conductance value is the direct consequence of the small energy difference between the electrodes’ Fermi energyEFand the molecular orbital which dominates HOMO or LUMO.Because the Kohn-Sham orbitals are mathematical objects rather than true molecular orbitals, their energies should be shifted, the calculated value of conductance may be larger than the experimental value.Some previous studies on single-molecule junctions in a solvent, considered the energy offset of the dominant molecular orbital relative to the electrode Fermi level, which obtained very meaningful results[38,39].Unfortunately, there is no experimental value of conductance of the GaN molecular chain to compare.But we expect that our theoretical prediction might be useful in further experiments and theories.
To further understand the conductance of the junctions, we analyze the transmission spectrumT(E,V=0) (See Fig.3), and the projected density of states (PDOS) (See Fig.4) of the GaN molecular chain at the optimal position.EFof Au is located at a peak in the transmission function.Thus,T(EF;0) is dominated by a resonance corresponding to the energy of the highest occupied molecular orbital (HOMO),εHOMO.This provides a large conductance, so the Au-(GaN)2-Au junctions have large transmission.By observing the Fig.4, we can find that the transport channel is mainly formed by thepxandpyorbital electrons of Ga and N atoms, with an almost negligible contributions from theirpzorbital electrons.

Fig.3 Transmission coefficient as a function of energy at the equilibrium position.
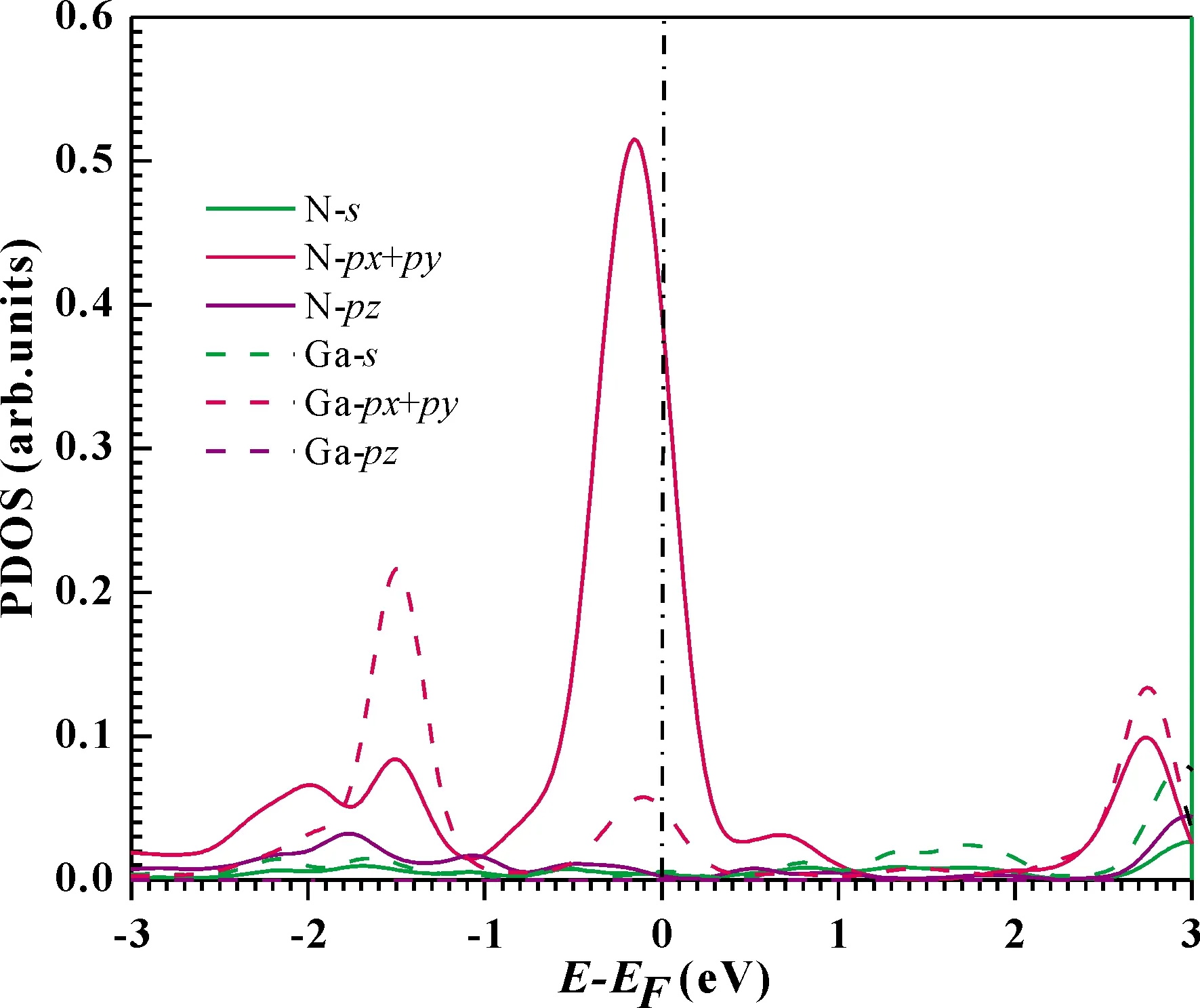
Fig.4 The PDOS for the GaN chain at the equilibrium position.
The current is self-consistently calculated within the non-equilibrium Green’s function approach with the voltage-dependentLandauer formula[40]
(5)
f(E-μL,R)=1/{exp[(E-μL,R)/kBT]+1},
(6)
wherefis the Fermi-Dirac distribution function of two electrodes withμL/R, the chemical potential for the left/right electrode.The results of relationship between current and bias voltage are shown in Fig.5 (circles and right-hand axis).We can easily see that the conductance (dI/dV) is larger for V < 0 than that for V > 0.This asymmetric shape is rationalized for the configuration, which can be due to an asymmetry in either the leads or in its couplings to the molecule, and the latter factor can be due to an intrinsic property of the molecule.Overall, theI-Vcurve displays a non-linear relationship, indicating that the junctions have a semiconductor-like characteristic.In order to achieve a qualitative understanding of the underling physics, it is useful to calculate the transmission coefficients as a function of the energy for different biases and configurations, because the current through the system is proportional to the integral of the transmission coefficients in the energy window (EF-eV/2,EF+ eV/2).The transmission spectrum ofT(E) is shown in Fig.3, under the bias of 0 V, 0.3 V, 0.6 V, 0.9 V.We can observe a significant drift of the HOMO resonance to lower energies as the bias increases.Such a drift of the HOMO makes the HOMO away from the Au Fermi level.Additionally, we can find, in the low bias zone (|V|< 0.3 eV), the transmission peak does not leave the energy window, and therefore the conductance remains relatively large which can be found in Fig.5 (squares and left-hand axis).However, when the external bias |V|> 0.3 eV, the HOMO drifts away from the Fermi energy, thus the conductance becomes small.
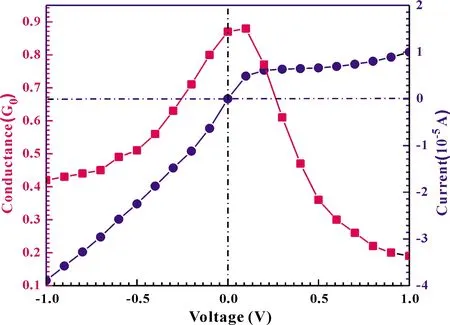
Fig.5 The conductance (squares and left-hand side axis) and the current (circles and right-hand axis) as a function of the bias.
4 Conclusions
To summarized, we have systematically investigated the transport properties of the GaN molecular chain sandwiched between two semi-infinite Au (1 0 0) metal electrodes by usingabinitodensity functional theory plus the non-equilibrium Green’s function method.We simulate the Au-(GaN)2-Au junctions breaking process and calculate the corresponding cohesion energy.The obtained conductance of the GaN molecular chain at the optimal position is 0.85G0.The transport channel is mainly formed by thepxandpyelectron orbitals of Ga and N atoms.Additionally, we also calculate the conductance and the current of the junctions at the equilibrium position under small voltage.It is found that: Firstly, with the increase of the bias voltage, the conductance of the GaN molecular chain always decreases; secondly, the shape of theI-Vcurve is asymmetric.Such behavior shows that the (GaN)2junctions have the characteristic of the semiconductor-like junction.It is expected that these results are useful in understanding the electronic transmission mechanism of GaN molecule and designing the GaN naoscale wires.
