Kaiser窗在滤波反投影图像重建中的应用研究∗

于尚民

（青岛大学电子信息学院 青岛 266071）

1 引言

重建算法是CT（Computed Tomography，计算机断层成像）图像重建技术的核心。迭代法和解析法是目前最常见的两大类重建算法。滤波反投影（Filter Back Projection，FBP）算法是一种最为常用的解析图像重建算法［1］。滤波反投影算法重建速度快、重建图像精度高，因而它是一种应用十分广泛的CT图像重建算法。在直接反投影算法中，重建后的图像是由所有方向下的投影数据累加而形成的。在累加过程中，无限空间中原本像素值为零的点的像素值被均匀地回抹为有限物体空间的投影值，即其值变为非零。这种非零的像素值导致了明显的“星”状伪影。由投影定理可知，在反投影重建之前将投影数据用滤波函数进行滤波可消除“星”状伪影［2］。因此，滤波反投影算法的关键在于滤波函数的设计。窗函数法常用于滤波函数的设计。R-L（Ram-Lak）滤波函数和 S-L（Shepp-Lo⁃gan）滤波函数是滤波反投影算法中典型的两种基于传统窗函数的滤波函数。其中R-L滤波函数是一种简单易行的滤波函数。它的重建图像质量较高，但却伴随着严重的吉布斯（Gibbs）现象［3］。Kai⁃ser窗是一种可由参数调节的窗函数，有着广泛的应用空间。本文将Kaiser窗滤波函数与基于传统窗函数的R-L滤波函数和S-L滤波函数进行对比，经实验验证，Kaiser窗滤波函的重建图像精度更高、抗噪能力更强。

2 滤波反投影算法实现原理

根据投影定理，在反投影重建之前将投影数据进行滤波，对滤波后的数据再进行反投影运算，可消除“星”状伪影。其具体步骤如下：

1）设 Sθ(ω)为某角度下的投影数据 pθ(t)的一维傅里叶变换；

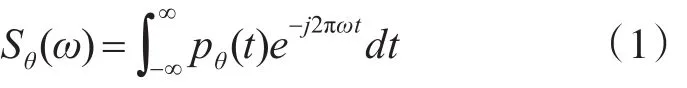
2）用一维权重因子 ||ρ乘以Sθ(ω)；

3）对第2）步所得结果作一维傅里叶逆变换，记为Qθ(t)；

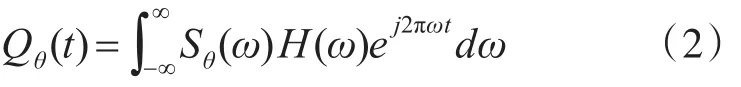
4）对 0°～180°内的全部修正过的 Qθ(t)作直接反投影运算，得到重建图像 f(x，y)。

3 滤波器的设计思想

滤波器设计的好坏会对重建图像的精度产生不可忽视的影响。FBP算法理论上要求滤波器的系统函数满足HR(ρ)= ||ρ，但现实中的滤波函数的频带宽度是无穷大的。在实际应用中，由Paley-Wiener准则可知，这种频带宽度无穷大的滤波器是无法实现的。但由于实际CT设备的分辨率是有限的，这使其收集到的投影数据是一种频谱能量分布于低频区域的密度分布［4］。因此可以忽略超出某个截止频率的投影数据，即

式（4）中的W(ρ)称为窗函数。W(ρ)的好坏对重建图像精度起着极其重要的作用。因此要求窗函数W(ρ)应遵守下列原则：

1）主瓣宽度要窄，提高识别精度，以增大图像分辨率；

2）最大旁瓣幅值尽可能的要小，增大阻带衰减、削弱Gibbs效应。

3.1 常用滤波器

3.1.1 R-L滤波器

R-L滤波函数频率响应为

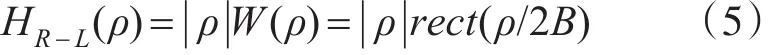
其中：

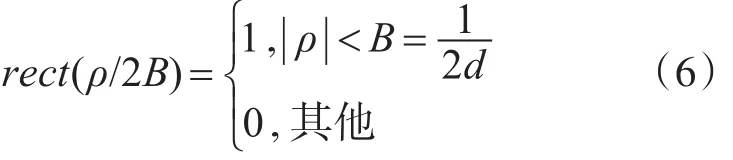
与滤波函数HR-L(ρ)相对应的卷积函数冲激响应hR-L(R)为

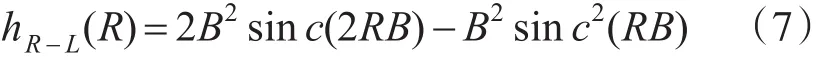
其中B=1/(2d)，sinc(x)=sin(x)/x。

其离散式（采样序列）为

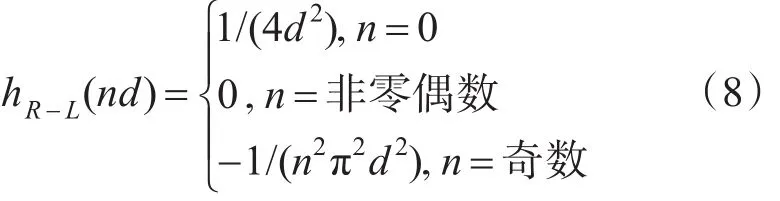
R-L滤波函数由于没有复杂的三角函数计算，因而运算速度较快。其所得重建图像较为清晰，但却伴随有严重的Gibbs现象，并对含有噪声的投影数据重建效果较差。

3.1.2 S-L滤波器

S-L滤波函数缓解了R-L滤波函数的震荡，其频率响应为

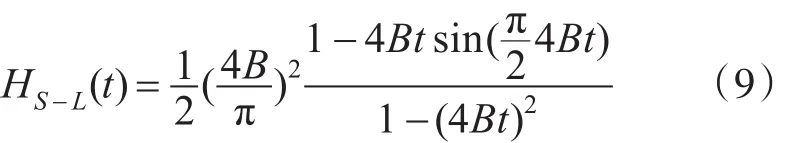
其离散表达式为

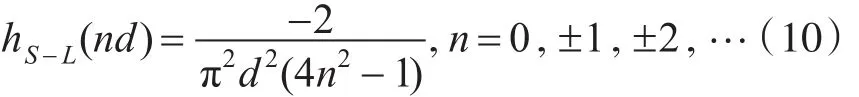
S-L滤波函数通过对投影数据中的高频成分的抑制，来减小Gibbs现象。同时S-L滤波器有着较强的抗噪能力［5］。但在低频段，其重建图像的质量不及R-L滤波函数，这是由于hS-L(ρ)在低频段偏离 ||ρ的原因。

除此之外，常用滤波函数还有三角窗滤波函数、Hanning窗滤波函数、Kaiser窗滤波函数等［6］。

3.2 图像评价指标

多数情况下肉眼难以分辨图像质量，因而需要引入量化评判判据，其表达式如下：

1）归一化均方距离d：

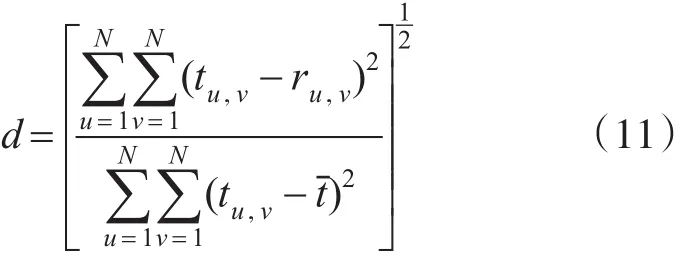
其中，N*N为图像的像素，tˉ为实际物体模型密度的平均值，重建图像和物体模型中第u行、v列的像素密度分别用ru，v和tu，v表示。d的值越大，表示CT重建图像和实际物体的偏差越大，图像越不清晰。d值受少数偏差大的像素点的影响较大。

2）归一化平均绝对距离r，即：

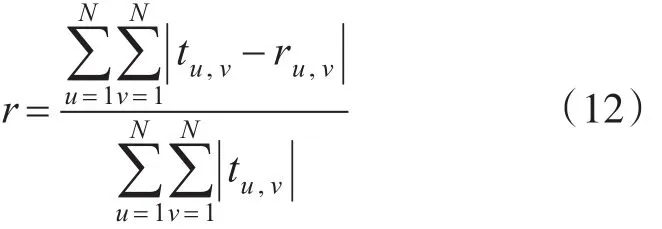
归一化平均绝对距离r与归一化均方距离d相比受少数偏差大的像素点影响较小。归一化平均绝对距离r反映了大多数像素点存在误差的情形。

依据归一化均方距离d和归一化平均绝对距离r两项指标，对矩形窗、S-L窗、Hanning窗、Ham⁃ming窗这四种窗函数的重建图像误差进行比较，如表1所示。

表1 窗函数滤波器的误差比较

由表1可知，加Hanning窗重建图像的归一化均方距离d和归一化平均绝对距离r要比其他三种窗函数要小，重建图像精度较高。

4 Kaiser滤波函数

4.1 Kaiser窗函数性质分析

Kaiser窗函数是一种常用的窗函数，其表达式为

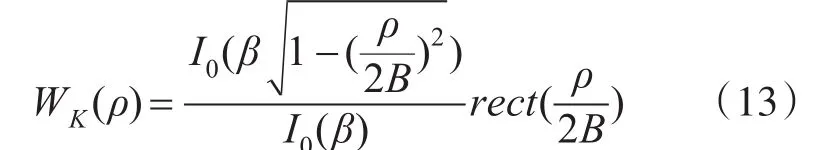
其中，Kaiser滤波函数时域内的主瓣宽度和旁瓣高低可以通过参数β来调节，β值越大，主瓣的宽度越大，旁瓣幅值越小，I0(x)为零阶第一类修正贝塞尔（Bessel）函数，其级数形式为

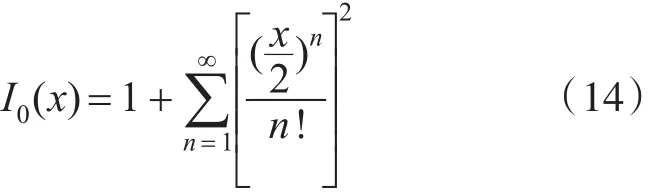
表2是Kaiser窗函数在不同β值下的性能。

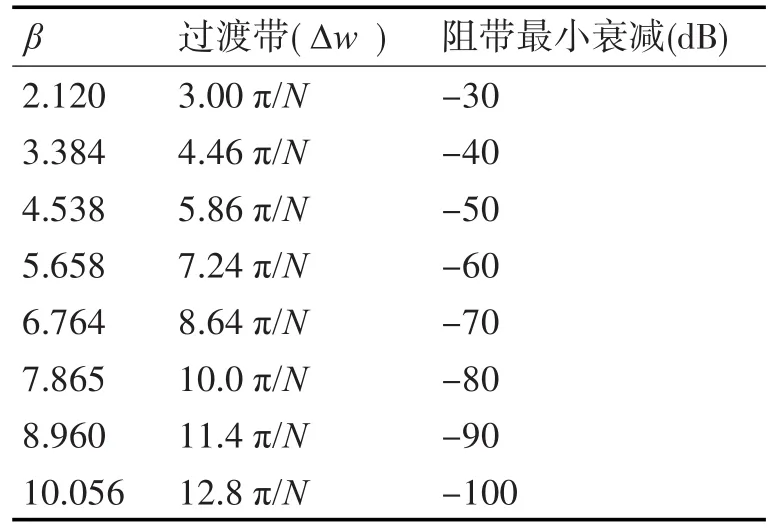
表2 Kaiser窗函数在不同β值下的性能

各窗函数（长度为64）的主瓣宽度和第一旁瓣衰减值如表3所列。

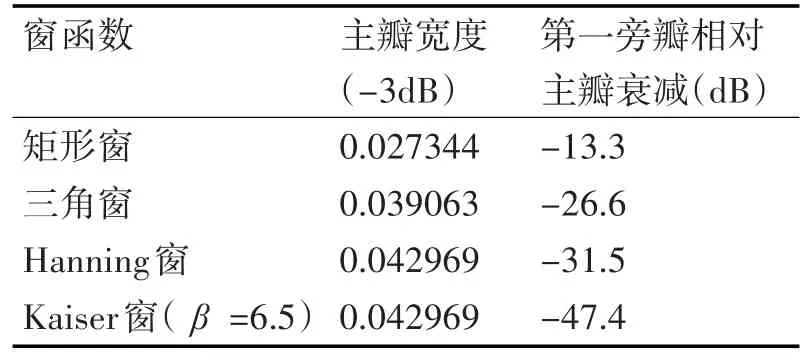
表3 主瓣宽度与第一旁瓣相对主瓣衰减值

由和表3可以看出，当β=6.5、长度为64时，Kaiser窗的主瓣宽度和Hanning窗主瓣宽度一样，但旁瓣幅值又比Hanning窗和矩形窗的小。根据滤波函数的设计原理和图像重建误差的影响因素可知，主瓣宽度越小，识别精度越高，图像重建的精度越高；旁瓣幅值越小，Gibbs效应越弱。因此，可以发现Kaiser窗滤波函数的空间分辨率、密度分辨率均较高，其图像重建的精度较高。

4.2 Kaiser窗函数实验结果检验与分析

实验中采用了二维平行束FBP算法进行计算机实验仿真来验证Kaiser窗滤波函数的图像重建精度。所用的投影数据由Shepp-Logan模型生成，其大小为512*512，重建图像的大小为514*514，三种滤波函数的重建图像如图1所示。

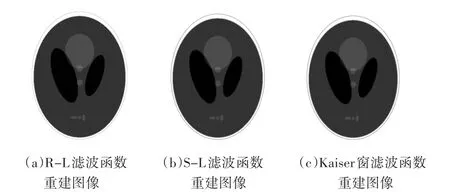
图1 三种滤波函数的重建结果

由表4可知，Kaiser窗（β=6.5）滤波函数重建的图像，其归一化绝对距离r和归一化均方距离d分别为0.1372和0.32537比R-L滤波函数和S-L滤波函数要小，因而图像重建精度较高。

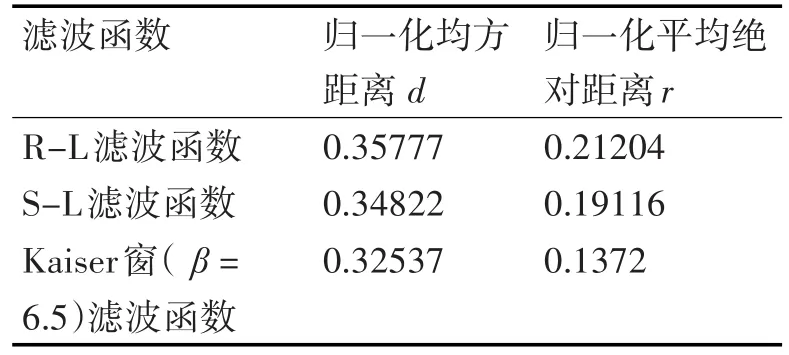
表4 三种滤波函数重建的d和r值

4.3 Kaiser窗在噪声环境下的重建结果分析

在实际CT数据的采集中，投影数据常常混杂有噪声。因此，本文引入了泊松噪声来对Kaiser窗滤波函数的重建图像精度进行分析。

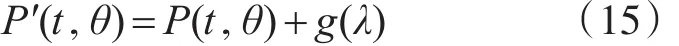
改变参数λ，就可以改变产生泊松噪声的大小。实验中选取大小为512*512的Shepp-Logan模型的投影数据。噪声测试中λ的取值分别为0.1，1，2。其重建图像如图2～图4所示。

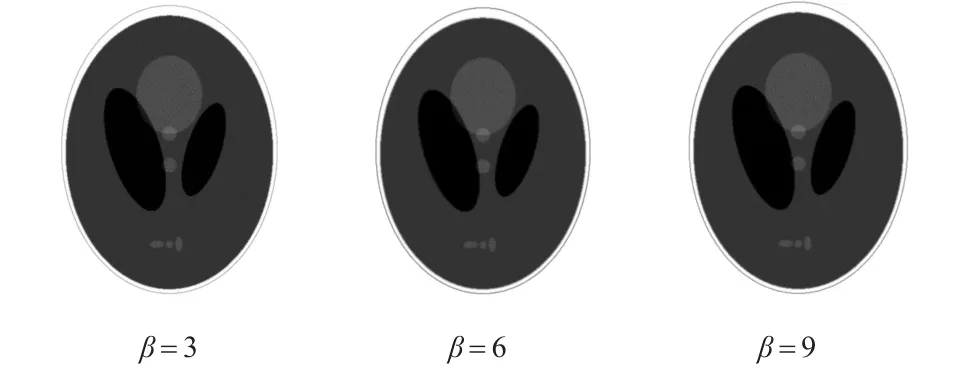
图2 λ=0.1时Kaiser窗滤波函数的重建结果

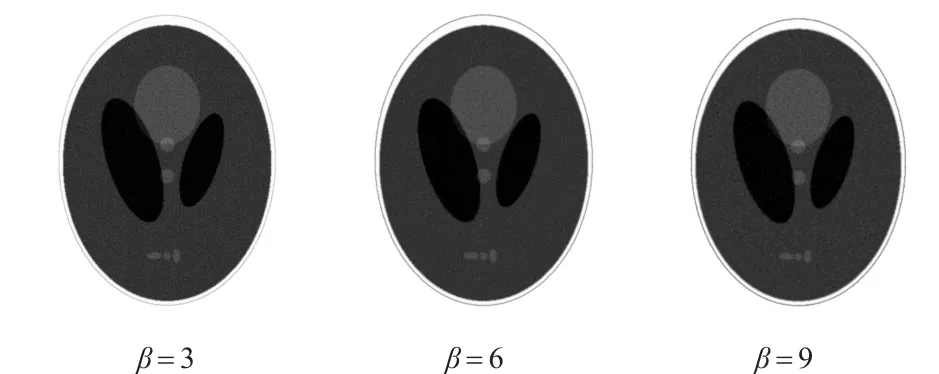
图3 λ=1时Kaiser窗滤波函数的重建结果

图4 λ=2时Kaiser窗滤波函数的重建结果

由图2～图4可以看出，Kaiser窗滤波函数在泊松噪声下仍然可以获得高精度的重建图像。

图5是对大小为512*512的Shepp-Logan模型的投影数据，以参数β为自变量，分别以归一化均方距离d和归一化绝对距离r为因变量，分析在λ=0.1、λ=1和λ=2的噪声情况下Kaiser窗滤波函数的β值对图像重建精度的影响曲线图。

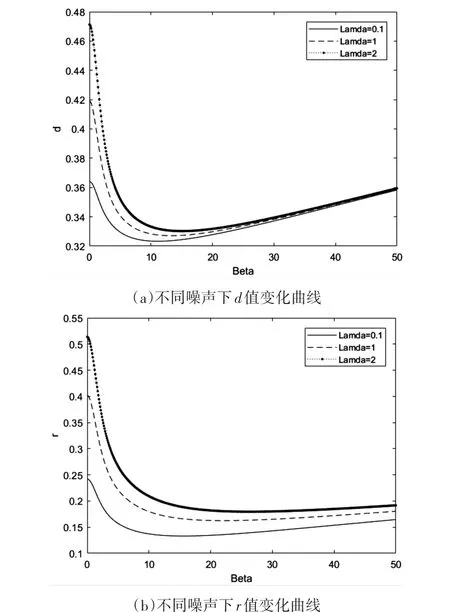
图5 评价函数变化曲线

由图5可以看出，在λ=0.1、λ=1和λ=2时，随着β的增大归一化平均绝对距离r和归一化均方距离d均呈先减小后增大的变化趋势。这是由于，当β增大时，Kaiser窗的旁瓣幅值减小，Gibbs效应减弱，同时主瓣宽度增加，识别精度降低。在曲线的前半段，旁瓣幅值减小的影响大于主瓣宽度增加的影响，故d和r减小；在曲线后半段，主瓣宽度增加的影响大于旁瓣幅值减小的影响，故d和r增大。对λ=1的d和r变化曲线分别进行拟合可得：

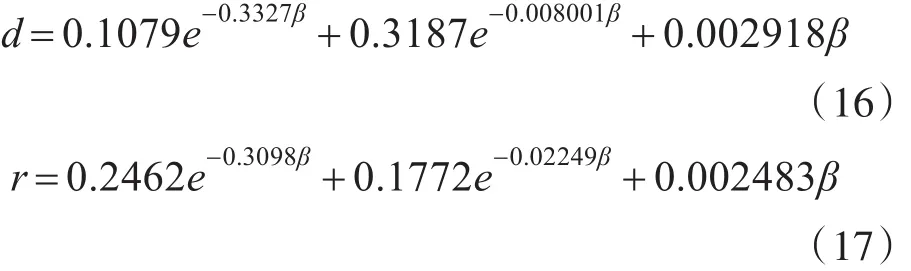
对式（16）、（17）求一阶导数可知，当β=12.2658时，d有最小值0.3265；当β=22.3863时，r有最小值0.1629，这与实验结果较为吻合。

经实验验证，一般当β≈0时，Kaiser窗滤波函数近似于R-L滤波函数；当β≈4时，Kaiser窗滤波函数近似于S-L滤波函数；当β≈5.15时，Kaiser窗滤波函数近似于Hamming窗滤波函数。当β值取得过大时，会使重建图像出现模糊。在实际应用中参数β的取值取决于多个方面的因素，例如CT投影数据的采集设备、投影数据中混有的噪声种类、原始物体模型的种类以及评价函数等。

5 结语

本文通过对Kaiser窗滤波函数重建图像的分析，计算了其归一化绝对距离r和归一化均方距离d，证明了Kaiser窗滤波函数的图像重建精度比基于传统窗函数的R-L、S-L滤波函数的更高。此外本文还分析了泊松噪声对Kaiser窗滤波函数重建图像的影响，验证了Kaiser窗滤波函数的抗噪能力，并通过曲线拟合的方法来确定最优的β值，证实了Kaiser窗滤波函数的优越性。