基于node2vec的社区检测方法∗

王慧雪

（1.武汉邮电科学研究院 武汉 430074）（2.南京烽火天地通信科技有限公司 南京 210019）

1 引言

真实世界中，大多数的系统都可以表示为复杂网络。万维网、通信网、交通运输网、电力网络、社交网络等许多现实网络都与人们的生活密切相关。复杂网络内部，有的节点相互连接紧密，有的节点相互连接稀疏，这个特性叫做网络的社区结构。发现这些社区结构，可以帮助我们分析以及预测网络中的结构和各个元素之间的交互关系，具有非常重要的意义。

针对社区检测的研究，国内外的学者们已经提出了很多方法。图分割法是最早的社区检测方法，其中K-L算法和谱平分法［1］比较比较典型。运用图分割法进行社区划分有一个明显的局限，就是需要事先知道社区的先验信息，即社区的大小和数量，因而很难得到精确的划分结果。

另一种应用广泛的方法为层次聚类法。分为分裂算法和凝聚算法两类。2002年，Girvan和Newman提出了GN算法［2］，是一种分裂算法，其流程为计算网络中每个连接的边介数，然后去掉边介数最大的边直到所有的边都被删除。该算法计算复杂度较高，不适用于大规模网络。GN算法没有终止条件，网络最终会被划分为单独的节点，对此，Newman等又提出了一种衡量网络划分质量的标准，模块度Q。模块度越大，代表着社区划分的结果越好。Newman等2004年提出了一种基于凝聚法的社区检测算法，快速GN搜索算法，FN算法［3］，它的思想是把网络中每个节点都看成一个独立的社区并计算Q值，然后合并有边相连的两个社区，计算此时的模块度增量ΔQ，选择增量最大的两个社区合并，重复这个过程，直到整个网络合并为一个社区。

近年来基于模块度优化的算法成为研究的热点。研究者们提出了许多智能优化的算法，如遗传算法、粒子群算法、模拟退火算法、蚁群算法等。这类算法把社区检测问题看成一个优化模块度有关的目标函数，寻找当模块度达到最大时的网络划分。本文不同于以上方法的研究，提出了一种基于node2vec的社区检测方法，利用 node2vec算法［4～6］将社区检测转换为机器学习中的聚类问题，该方法中首先使用biasα random walk策略［7］生成一系列序列，然后使用Skip-Gram模型［8］去训练特征向量，训练出的特征向量对节点之间的同质性假设和结构性假设都有很好的刻画。最后，分别使用K-Means［9］、DBSCAN［10］、SOM 聚类算法［11］对训练出的特征向量进行聚类，聚类的结果即为最终的社区划分，同时对这三种聚类结果进行对比分析。本文分别使用人工合成网络和真实网络作为实验数据，通过仿真证明了本文提出方法的可行性。

2 基于node2vec的社区检测

2.1 随机游走策略

2.1.1 随机游走

node2vec算法中提出一种带权重的随机游走算法—biasαrandom walk，该算法可以使训练出的向量同时满足节点之间同性质与结构相似性假设。在该算法中，给定一个源节点μ，我们假设随机游走的步长为固定长度L，从源节点μ开始，使用如下分布产生邻居序列：

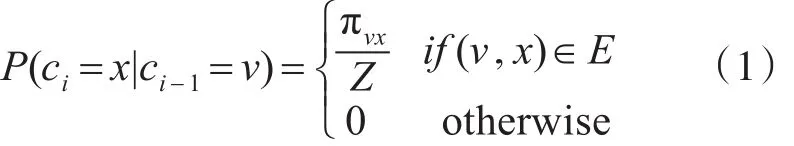
ci代表随机游走中的第i个节点，πνx表示节点ν到节点的转移概率，Z为归一化因子。

2.1.2 带偏置的搜索算子

随机游走最简单的方法是根据边的权重ωνx抽取下一个节点，此时 πνx=ωνx，然而，当检测两种不同类型的网络社区时，这并不能划分出网络结构，也不能指导我们去搜索。另外，不同于BFS和DFS这类极端采样相同结构和性质的范例，我们的随机游走应该适应于这样一个事实，即这些相同的节点并不是竞争性和排他性的，真实世界的网络通常表现出BFS和DFS的混合。

我们定义一个带有两个参数 p和q的二阶随机游走来控制游走。假设随机游走要经过边edge(t，x)，当前处于节点ν。游走到下一步时需要计算从节点ν经过边edge(t，x)的转移概率。转移概率 πνx=αpq(t，x).ωνx，αpq(t，x)由式（2）给出，其中t表示上一个节点，ν代表当前节点，x为下一个可能的节点。

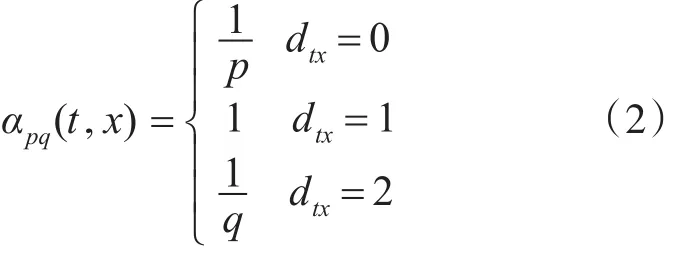
如图1表示了node2vec中的随机游走过程。游走从t到ν，现在需要计算离开节点ν的下一步骤。边上的标签代表了带偏置的搜索算子α。dtx表示节点t和节点x之间的最短路径。

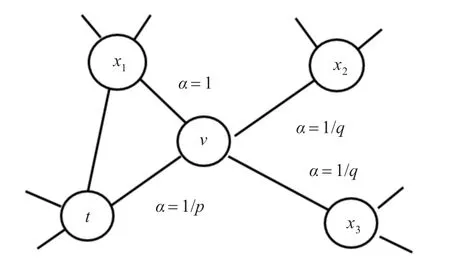
图1 邻居节点估计示意图

直观上来看，参数 p和q控制搜索速度以及离开源节点μ的邻域，这两个参数使我们搜寻的过程在BFS和DFS之间取得平衡，因此，既反映了节点的同质性，又反映了结构相似性。

返回参数 p。参数p控制返回上一节点的可能性。给该参数设置较大的值可以降低在接下来的两个步骤中采样到已经访问过的节点的概率。这种策略仅考虑当前节点的源节点2-hop内的节点。如果 p值很小，则将会导致游走在源节点μ附近。

深度控制参数q，如果q＞1，则偏向于遍历临近t节点的节点，这种游走类似于BFS；相反，如果q＜1，则偏向于遍历远离t节点的节点，这种行为反映了倾向于向外探索的DFS，然而这里的一个重要区别是我们实现的类似于DFS的搜索是在随机游走的框架下进行的。因此，这些采样的点从给定源节点并不是非常严格的增加距离，反而使我们受益于简单的预处理和随机游走的高效采样率。

2.2 Skip-Gram模型

Skip-Gram是一种语言模型，该模型能够极大化单词出现在上下文中的概率。它是使用一个单词来预测句子。该模型优化的目标函数由式（3）给出：

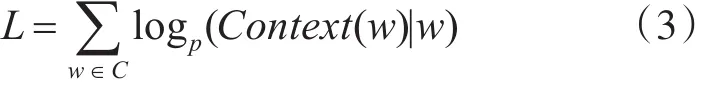
其中w表示当前词，Context(w)表示词的上下文，C表示语料库。可以理解为该模型先利用文本语料库构造词汇表，然后学习词的向量表示。在本文中，该语料库为网络中的节点随机游走后产生的线性序列。具体模型如图2所示。

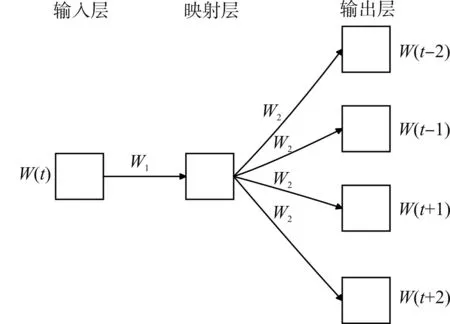
图2 Skip-Gram模型框架结构

从图2可看出，该模型由输入层、映射层和输出层组成。其中，W1为输入层和映射层之间的权重矩阵，W2为映射层和输出层之间的权重矩阵。输入为one-hot编码的形式，该模型的原理可以理解为在一个句子或者文本中，选择任意一个单词用其向量表示，使这个向量能够预测到其周围的单词，即该模型的训练目标为给一个单词序列，使式（4）的值最大。

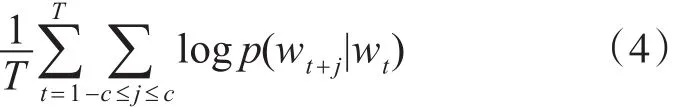
其中，T为训练文本的大小，c为窗口的大小，wt为任意一个单词的向量，wt+j为前后 j个单词，计算条件概率p(wt+j|wt)的公式如下：

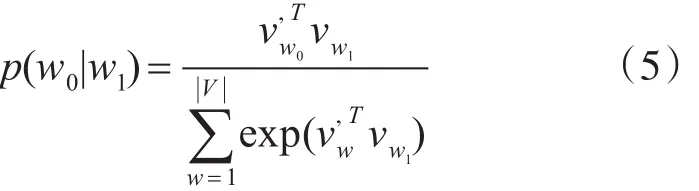
其中，w1为当前输入单词，w0为当前输出单词，vw和分别是词的输入和输出。本文中，我们把随机游走后的线性序列看成输入的单词，把经过训练后预测到的输入单词附近单词的向量形式作为特征向量，该特征向量携带有每个初始输入节点的特征，接下来对其进行聚类。

2.3 特征向量聚类

上面我们使用node2vec算法对节点进行训练后，得到网络节点的最佳特征表示，如何对这些特征进行聚类，划分社区结构是我们需要重点关注的问题。

目前有大量的聚类算法，但不同的方法适用于不同类型的数据，想要得到好的聚类结果，可以通过对相同的数据尝试多种聚类算法。在本文中，我们选用基于划分的方法K-Means算法、基于密度的方法DBSCAN算法、基于模型的方法SOM算法这三种算法对特征向量进行聚类。

K-Means算法是划分方法中较为经典的算法，该算法效率很高，但需要事先指定划分簇数k，针对k值的确定，本文先使用传统的社区检测算法进行社区检测，然后把检测结果中社区的个数作为K-Means算法中的k值。

DBSCAN算法是一种基于密度的聚类算法，不需要事先确定划分的簇数，而且其最大的优点为能够发现任意形状的簇，聚类效果较好。

SOM聚类算法是一种竞争学习型的无监督神经网络算法，它通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数和结构。

这三种聚类算法各有优劣，我们需要通过实验进一步证明使用哪种聚类算法聚类特征向量，社区检测的准确率更高。

3 算法流程

基于node2vec的社区检测方法的流程图如图3所示。

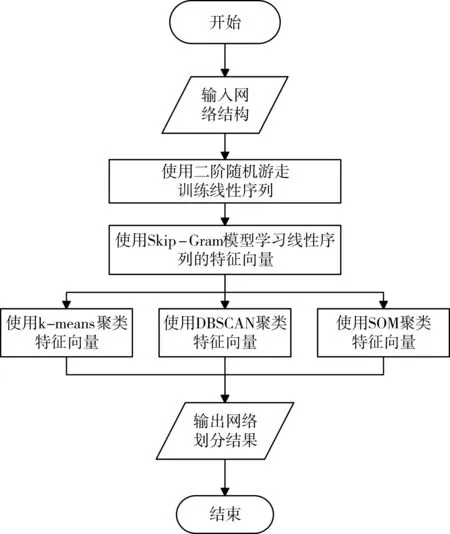
图3 基于node2vec社区检测方法流程图

基于node2vec的社区检测方法步骤如下：

输入：邻接矩阵表示的网络图G(V，E)

输出：对网络划分的结果

步骤1：转移概率预处理。定义由当前节点转移到下一节点的概率πνx；

步骤2：随机游走。根据转移概率的预处理得到G，(V，E，π)，以网络中的每个节点为初节点进行随机游走；

步骤3：使用Skip-Gram模型训练特征向量。输入为步骤2随机游走后得到的线性序列，目标是对隐藏层进行优化，希望输入为某个节点时，输出为其同质性或同构性的节点的概率最大。优化的过程如下：

1）前向传播：对网络节点进行one-hot编码，初始化隐层加权矩阵Φ：WN×d和隐层-输出层加权矩阵，在输出层计算条件似然概率，并与预测节点的one-hot向量求差作为误差向量；计算各误差向量对应的元素和；

2）反向传播：根据前向传播过程中产生的误差，采用链式求导法则，将其反向传播到隐层，更新权重矩阵，采用更新过的加权矩阵，迭代前向传播过程，直到条件似然概率取得最大值，此时隐层加权矩阵即为网络节点的最佳特征表示。

步骤4：使用K-Means聚类算法、DBSCAN聚类算法、SOM聚类算法对步骤3得到的特征向量进行聚类；

步骤5：得出划分结果，并对比使用三种聚类算法得到的网络划分的优劣。

4 实验仿真

4.1 实验评价标准

标准化互信息（NMI）［12］常用在聚类中，度量两个聚类结果的相近程度，在社区检测中是衡量真实的网络划分与社区检测得到的网络划分相似性的方法。对于两个不同的划分结果A和B，NMI定义如下。

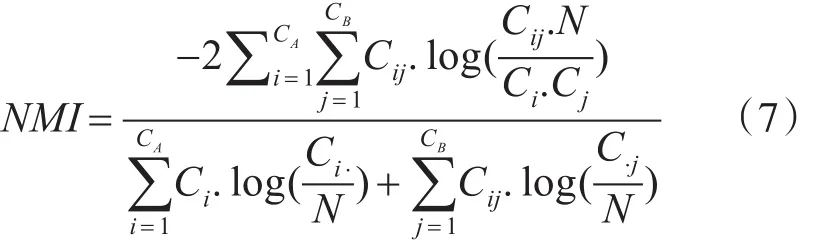
其中，N为节点的个数，C是一个混合矩阵，其中的元素Cij表示划分结果A中的社区i在划分结果B中的社区 j里面也出现的个数。CA表示划分结果A中社区的个数，CB表示划分结果B中社区的个数。Ci⋅中表示C中第i行元素的总和，C⋅j表示第 j列元素的总和。NMI值越大，A划分和B划分的相似度越大，当NMI为1时，说明A和B的划分完全一致。

Newman 和 Girvan 定义了模块度［13］（modulari⁃ty）为评价网络社区划分优劣的指标。Newman认为一个合理的社区就是将划分出的网络与随机网络进行比较，划分出的网络与随机网络的期望差值越大，表明该网络的社区结构越明显。模块度可定义为如下。

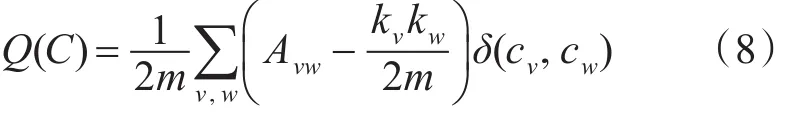
其中，m为网络的总边数，Avw有两种取值，取值为1时代表节点v与节点w之间有连接的边，取值为0时代表节点v与节点w之间无连接的边，kv为节点v的度，当节点v与节点w在同一个社区时，δ(cv，cw)=1，否则为0。

4.2 人工合成网络

本文所使用的人工合成网络是Lancichinetti等提出的基准网络，该模型引入了一个混合参数μ来调节网络的拓扑结构，该参数表示的是社区内节点和外节点的连接紧密程度，通过调节该参数，可以给实验提供包含不同社区结构的网络类型，μ越小，表明社区结构越清晰，网络越具有较强的社区结构，随着μ的增大，网络的社区结构越模糊。μ的物理含义是节点外度占总节点的比例，以0.5为界，小于0.5时，说明节点内度大于节点外度，具有较强的社区结构；大于0.5时，说明节点内度大于节点外度，网络的社区结构较模糊。我们以0.5为界，在0～0.5之间均匀的选取11个点进行实验。

我们将使用K-Means聚类的基于node2vec的社区检测算法简称为NK（Community Detection Based on Node2vec By Using K-Means）；使用 DB⁃SCAN聚类的基于node2vec的社区检测算法简称为ND（Community Detection Based on Node2vec By Us⁃ing DBSCAN）；使用SOM聚类的基于node2vec的社区检测算法简称为NS（Community Detection Based on Node2vec By Using SOM）。本文将NK算法、ND算法、NS算法与传统的社区检测算法GN算法、Louvain算法在人工合成网络上进行对比实验。

从图4可以看出，当 μ≤0.3时，NK、ND、NS、GN、Louvain算法的NMI值都为1，此时它们都能准确的发现网络真实的社区结构，从μ开始，传统社区检测算法GN算法、Louvain算法的NMI值开始下降，表明社区检测的结果越来越不准确，ND算法在 μ=0.35时NMI值开始呈下降趋势，而当μ=0.4时，NK、NS算法的NMI值才开始下降，这说明了当社区的结构模糊度有所降低时，基于node2vec的社区检测方法比传统的算法划分的更准确，当μ继续降低，大于0.4时，此时社区的结构已经变得更加模糊，传统算法GN算法和Louvain算法迅速下降到0.4以下，而基于node2vec的社区检测方法的NMI始终高于对比算法，其中NS算法在μ=0.5时NMI值还达到0.45左右。综上所述，基于node2vec的社区检测算法在人工合成网络中性能更加优越。

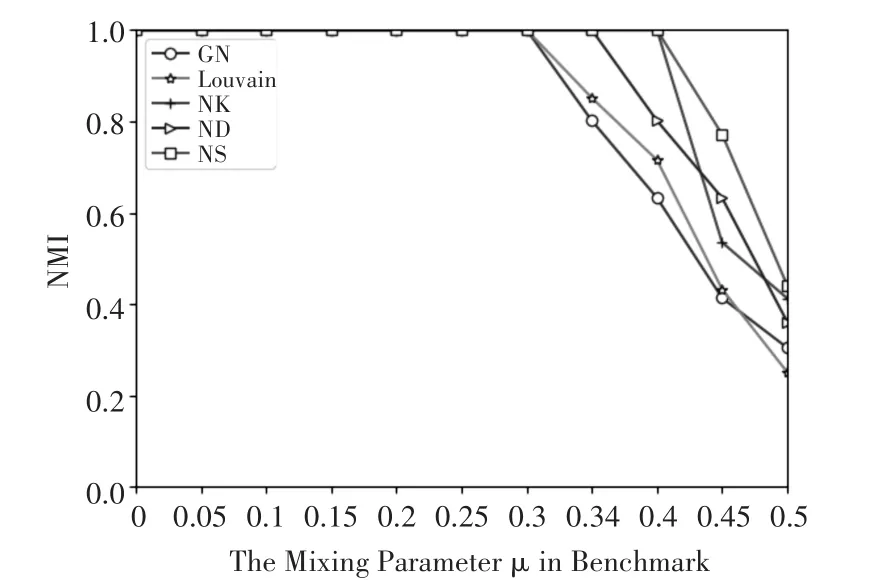
图4 各算法在Benchmark网络上NMI对比

4.3 真实世界网络

本文使用四个经典的真实网络进行实验仿真，分别为空手道俱乐部网络（Karate Network）、海豚网络（Dolphins Network）、美国足球联赛网络（Foot⁃ball Network）、美国政治书网络（Books Network），下表给出了这四个真实网络的边和节点信息。

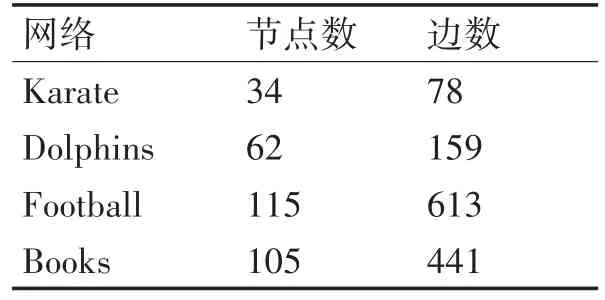
表1 四种真实网络的特性

对于这四个真实网络，本文把基于node2vec的社区检测方法和对比算法独立运行了20次，使用模块度Q作为评价指标，选出最大Q值（Qmax）和平均Q值（Qavg）图5为实验结果。

从图5可以看出，基于node2vec的社区检测方法NK、ND、NS算法在四个真实数据集下与传统社区检测算法GN算法、Louvain算法相比较，Q值有所增大，说明新算法社区检测的准确率有了提高。其中NK算法总体要优于ND算法，但NK算法有一个弊端，就是要事先给定划分的簇数，对此本文将传统算法检测出的社区个数作为NK算法确定簇数的依据。NS算法在Karate网络和Dolphins网络中检测准确率最高，随着数据量的增大，出现学习过度的现象，在Football和Books网络中检测准确率有所降低。

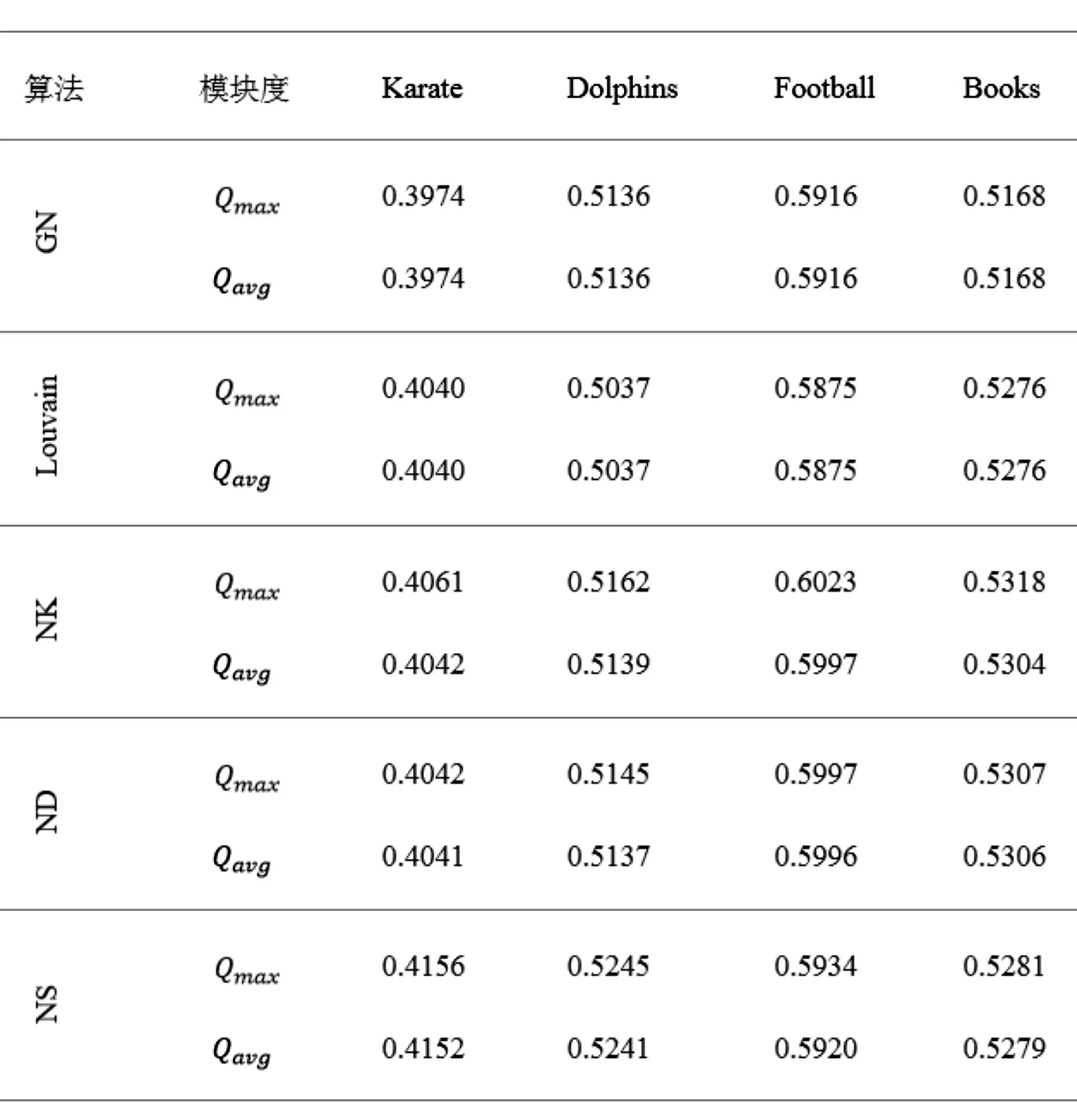
图5 几种算法在四个真实网络下的模块度对比

本文通过实验证明了基于node2vec的社区检测方法的有效性，与传统的社区检测方法GN、Lou⁃vain相比，具有很强的竞争力。

5 结语

本文提出了基于node2vec的社区检测方法，该方法首先使用node2vec算法把网络中的节点通过训练转换成网络节点的最佳特征表示，再选取三种典型的聚类算法对该特征进行聚类，聚类的结果即为社区的划分结果。使用node2vec算法的关键在于将社区检测转化为机器学习中的聚类问题。本文通过实验比较了这三种聚类算法的优劣，同时，实验对比了传统的社区检测算法GN算法、Louvain算法，证明了基于node2vec的社区检测方法的有效性。