串联模块式航天器基频分解技术研究

蔡一波 杜冬 孔祥宏 胡梦遥 陶炯明

(上海卫星工程研究所，上海 201109)

空间站、深空探测等航天任务是当前及后续航天活动的重要内容，大型化模块化是其主要特征。这些航天器在发射过程中要经受严酷的力学环境，其中重要的一部分就来源于通过星箭对接面传递的低频振动环境[1-2]，为了防止结构受到损坏，航天器的固有频率应避免与运载火箭的固有频率发生耦合，因而在设计时就要对航天器的固有频率给予考虑。运载研制方对航天器研制方提出的基频要求是针对整星的要求，但航天器各个模块的设计常常是分配给各分系统研制单位的，例如拟于2020年发射的火星探测器，其环绕器和着陆器就是由不同单位研制的。因为当前理论研究的缺失和工程方法的不完备，还缺乏有效的分解方法，很容易出现单个模块设计指标难以明确或反复调整，航天器整体固有频率不满足要求导致重复设计的情况。所以在研制初期，设计人员往往为了避免上述情况发生，制定更保守的指标，留出较大的余量，但这样会带来不必要的设计代价。

文献[3]提出开展结构动态设计的研究，力争在初样阶段就全面地考虑对结构的静、动等各方面的要求，是提高设计水平的一个重要途径。文献[4]认为在航天器研制过程中，如何通过设计要求分配和指标分解等顶层设计实现整形动力学特性的优化和控制，一直是亟待攻克的技术难题。因此，在总体方案制定初期，应通过对整星进行合理的动力学研究和设计[5-8]，实现各模块研制单位设计的“快、好、省”，进而缩短研制周期，避免“过设计”，提高卫星载重比。

为了解决弹性连续体基本固有频率分解的问题，文献[9]提出了一种基于约束子结构法的刚度分解方法。此方法虽然成功地求出了连续体结构基本固有频率的下限，但下限公式中的参数实际物理意义并不明确，难以在工程中进行测量和判断，限制了可操作性。文献[10-11]也根据分解刚度法，分别对某卫星和30 m望远镜三镜系统的基频进行了分解，但两者在应用于复杂结构时误差都较大。文献[12]基于悬臂梁假设，求得一般情况下串联悬臂梁结构基频的解析解，并将其简化为3种极端情况下的理想模型，定性分析了理想模型与实际模型之间基频的误差，但没有给出严格理论证明，而且没有对复杂模型的适应性进行分析。

本文在参考文献[12]的基础上，从简单的串联悬臂梁分析到复杂的卫星结构，利用蒙特卡洛算法评估误差大小，从工程上为航天器总体设计提出一种行之有效、操作简便且不失精确的频率指标分解方法。

1 理论证明

多自由度系统振动的基频满足如下瑞利商公式

(1)

式中：K和M分别表示系统的刚度阵和质量阵；φ表示振型空间Η内的任意振型。当φ使瑞利商取极小值时，ω0对应系统的基频，φ对应基频的振型。

对于底部固定的航天器而言，K和M均为对称正定阵。定义系统参数变化ΔK和ΔM，系统参数变化后的基频表达式为

(2)

如果ΔK正定，ΔM负定，对∀φ∈Η

(3)

所以必有

(4)

式(4)表明，将系统中的任意一个局部区域刚度增大或者质量减小，同时保持该区域与其它部分的连接关系不变，则新系统的基频必定高于原系统的基频。

对于大型串联模块航天器而言，发射状态下为底部固支结构，如图1所示。

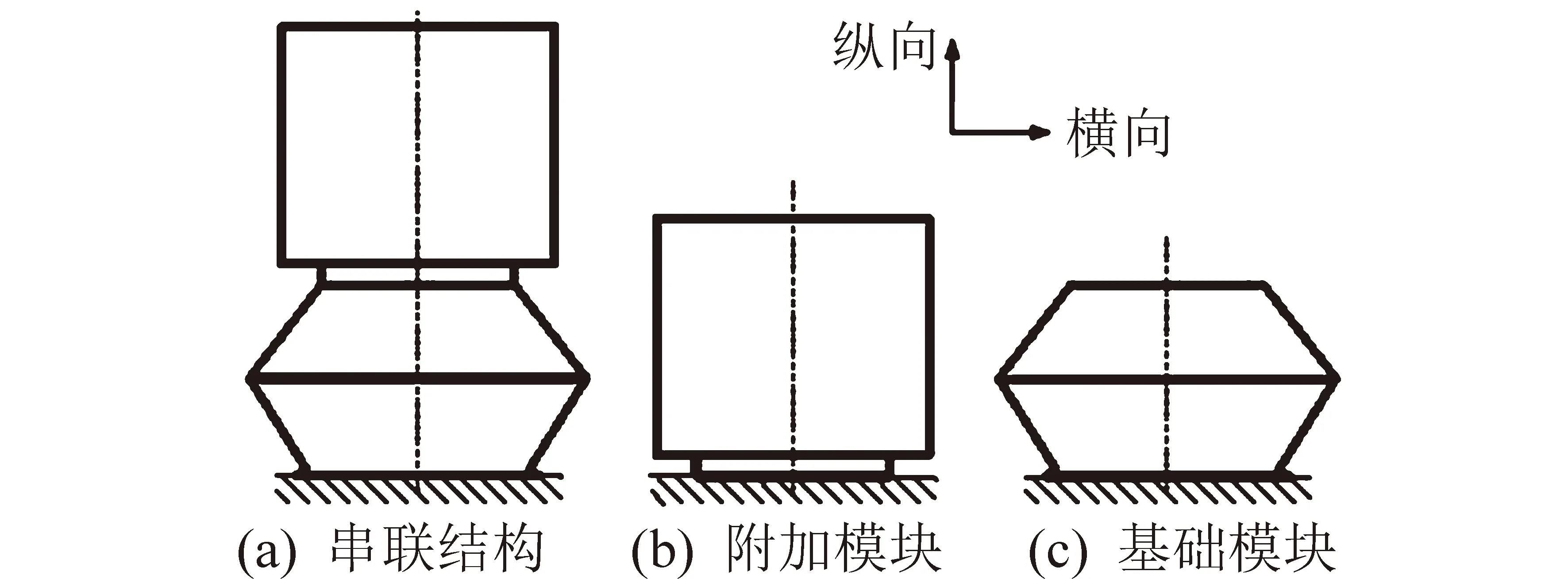
图1 航天器串联模块示意图Fig.1 Schematic diagram of satellite tandem structure

图1以连接界面为分割线，上部为附加模块，底部为基础模块。选择将附加模块的刚度提升到无穷大即成为理想刚体，系统基频必然会提升但只要基础模块存在就不会趋于无穷，可以作为逼近策略之一，定义为系统Ⅰ。同理，将基础模块的质量降低到零即成为理想弹簧，系统基频必然也会提升但只要附加模块存在就不会趋于无穷，作为逼近策略之二，定义为系统Ⅱ。在系统Ⅱ的基础上又提升附加模块的刚度到无穷大(或者在系统Ⅰ的基础上又降低基础模块的质量到零)，系统基频还会进一步提升但同样不会趋于无穷，这个简单系统由理想弹簧和刚体组成，便于快速估算，定义为系统Ⅲ。现实系统定义为系统Ⅳ。那么4个系统之间的基频必然存在如下关系：

ω0,Ⅳ<ω0,Ⅰ<ω0,Ⅲ,ω0,Ⅳ<ω0,Ⅱ<ω0,Ⅲ

(5)

或

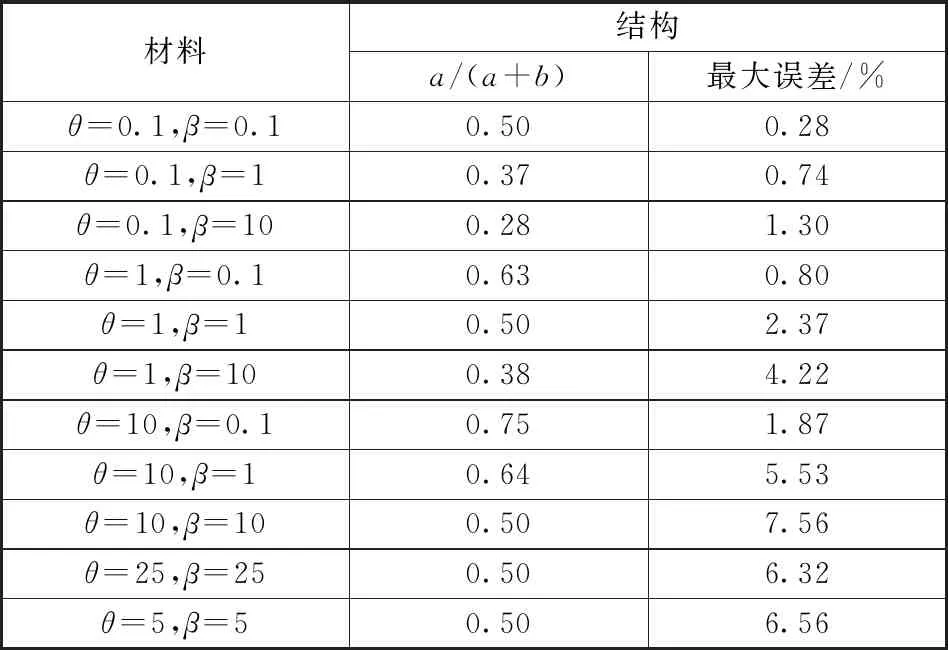
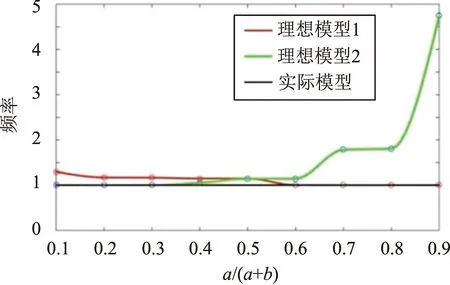
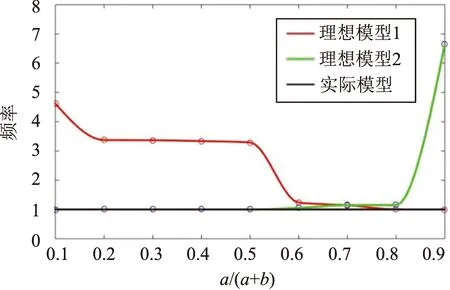
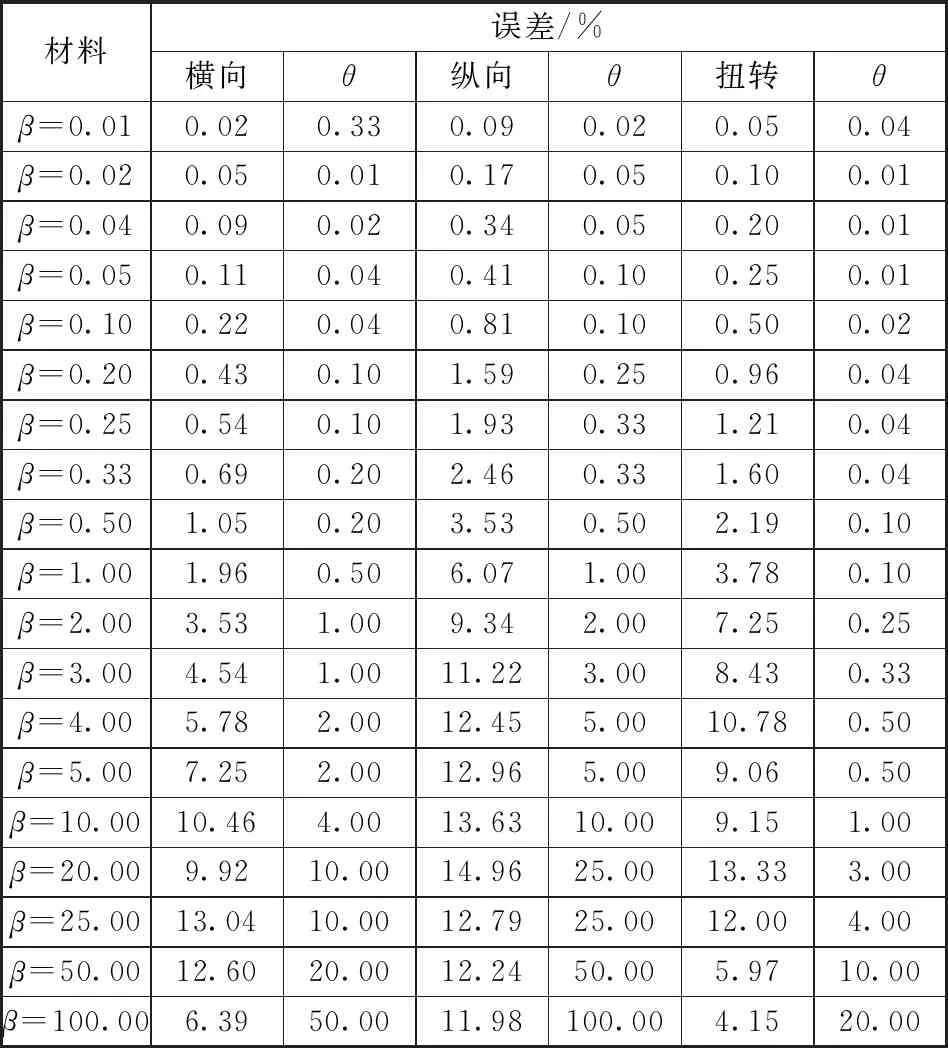
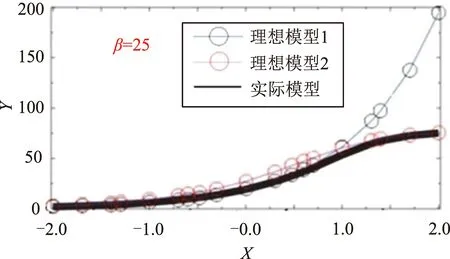
ω0,Ⅳ

(6)

至此，我们严格证明了文献[12]基于数值分析提出的猜想，即对于多自由度系统，3种理想模型的基频为真实模型基频的上限。同时还要指出，文献[12]计算的9种状态所绘制的个别曲线图出现了系统Ⅳ基频略高于系统Ⅰ、Ⅱ的情况，显然与理论证明结果式(6)不符。因为其在计算悬臂梁基频ω时采用了静变形假设，这也是推导过程中唯一的误差来源，而ω大于悬臂梁基频的精确解ω＇，进一步导致串联悬臂梁的计算结果也略微偏离了理论证明结果。

(7)

式中：悬臂梁抗弯刚度为EI；密度为ρ；长度为L。

另外，底部固支的航天器，与悬臂梁特性接近，我们知道其一弯模态、扭转模态和纵向模态振型特征差异鲜明，各自的振型空间是彼此无交集的，可将振型空间Η分解出3个不相交的子空间，即一弯振型子空间ΗB、扭转振型子空间ΗT和纵向振型子空间ΗL。式(5)针对指定的子空间仍然适用，这意味着，无论是一弯的基频、还是扭转或纵向的基频，都可以借助模型Ⅰ、Ⅱ、Ⅲ、Ⅳ系统分别对一弯、扭转或纵向的基频进行分析。本研究的基本思想就是用ω0,Ⅰ和ω0,Ⅱ逼近ω0,Ⅳ，并试图评估逼近误差。

2 数值解析计算

用ω0,Ⅰ和ω0,Ⅱ逼近ω0,Ⅳ，关键问题是逼近误差。量纲分析指出[12]，结构共振频率与材料模量、密度和结构几何尺度有关。分析可知，当给定几何尺度，附加模块相比于基础模块刚度或材料模量越大，其本身就越接近于刚体，则ω0,Ⅳ就会越接近ω0,Ⅰ。基础模块质量或材料密度相比于附加模块越小，其本身就越近似于零质量弹簧，则ω0,Ⅳ就会越接近ω0,Ⅱ。分割线(连接界面)越靠近底部固支区域，基础模块外形尺度相对于附加模块就越小，则其质量相对于附加模块就越小，刚度相对附加模块就越大，对应地ω0,Ⅰ就会越偏离ω0,Ⅳ，ω0,Ⅱ就会越接近ω0,Ⅳ，反之，连接界面越远离底部固支区域，ω0,Ⅱ就会越偏离ω0,Ⅳ，ω0,Ⅰ就会越接近ω0,Ⅳ。

串联悬臂梁模型如图2所示，其中y(x)为变形位移，基础模块梁密度为ρ1，抗弯刚度为E1I1，长度为a，附加模块梁密度为ρ2，抗弯刚度为E2I2，长度为b，l为串联梁总长，y0为悬臂梁末端位移。定义基础模块梁和附加模块梁长度、模量和密度之比分别为

(8)

图2 串联悬臂梁简化图Fig.2 Simplified diagram of tandem cantilever

但上述计算中存在以下不足：①基础模块和附加模块梁的密度和模量都是均匀的，而实际工程中结构的材料特性并非如此；②计算所用的公式是利用静变形推导出来的，存在误差；③只能计算一阶横向基频。因此，仍需利用仿真对更一般的情况进行更准确的分析。

表1 不同材料特性最大频率误差和界面位置

3 建模仿真计算

在实际工程设计中，工程师们不仅需要考虑结构的一阶横向频率，往往也需要考虑一阶纵向频率和绕纵轴的一阶扭转频率大小。因此为了进一步准确分析理想模型和实际模型3种频率之间的误差大小，现通过有限元分析，结合Abaqus软件二次开发功能，利用python语言编写脚本，实现在不同结构和材料参数下的循环建模仿真，并分析数据。

3.1 串联悬臂梁建模仿真

将均匀截面串联悬臂梁分成数个单元，划分基础模块和附加模块的界面在单元间连续变化，同时借鉴蒙特卡洛算法的思想，以最底部1个单元为基准，随机对其余单元赋材料密度和刚度特性，共计9000种情况，通过计算分别得到理想模型与实际模型3种频率对应的散点图，如图3所示，其中横坐标为界面位置，纵坐标为对实际模型归一化后频率(无量纲)大小。

图3 变界面串联悬臂梁频率曲线图Fig.3 Frequency curve of tandem cantilever beam with variable interface

由计算所得离散数据可得：一阶横向弯曲频率最大误差约为14.12%，一阶纵向频率最大误差约为14.40%，一阶扭转频率最大误差约为14.40%。由前文分析可知，当结构材料确定，ω0,Ⅰ=ω0,Ⅱ时，理想模型与实际模型的频率误差最大，但离散数据点对应的ω0,Ⅰ和ω0,Ⅱ不一定相等。

因此为获得更准确的误差上限，利用离散数据求得立方插值曲线(见图3)，找出两理想模型频率曲线的交点，视为最大误差对应位置。其中，一阶横向弯曲频率最大误差为14.12%，一阶纵向频率最大误差约为14.61%，一阶扭转频率最大误差约为14.61%。

综上所述，对于任意的串联悬臂梁结构，我们进行了大量的仿真计算，得到了足够多的数据表明：在工程应用范围内，将其在任意界面划分为基础模块和附加模块，其两种理想模型和实际模型的一阶频率误差上限为15%。但这一结论背后的理论原理尚不明了。

而对于串联模块式复杂结构而言，我们可以提出猜想，其两种理想模型和实际模型的一阶频率误差上限也为15%，并利用仿真分析进行验证。

3.2 串联舱段卫星建模

串联舱段卫星虽然一定程度上可以近似简化为悬臂梁结构，但两者之间必定存在误差，为验证前文的结果，本节进行复合材料串联舱段卫星不同材料参数情况下的循环仿真分析。

表1为不同材料参数下(θ、β)理想模型与实际模型3种频率的最大误差。

表2 串联卫星不同材料频率最大误差

由表2可知，在串联舱段卫星尺寸固定时，改变其材料参数，当θ=10,β=25时，理想模型与实际模型一阶横向弯曲频率的误差最大，为13.04%；当θ=25,β=20时，一阶纵向频率误差最大，为14.96%；当θ=3,β=20时，一阶扭转频率误差最大，为13.33%。图4分别为β=25和β=20时的归一化后频率曲线图，其中横坐标为θ以10为底取对数，纵坐标为频率大小。

由上述误差可知3.1节的猜想成立，即串联舱段卫星理想模型与实际模型一阶频率的误差上限为15%。

4 结论

根据上述分析，可以提出一种串联舱段卫星一阶频率总体指标的分解方法。

在卫星研制初期阶段，各分系统研制部门应估算附加模块的质量特性，包括质量、质心和惯量，以及整星的外形尺寸，再利用单自由度弹簧振子原理，结合估算出的质量特性和运载对整星的频率要求ω0，估算出基础模块的等效静刚度，包括线刚度、角刚度和耦合刚度，最后对各分系统研制部门有如下要求。

(1)对于基础模块研制部门：基础模块在顶部连接了质量特性与附加模块完全相同的刚体之后，一阶横向弯曲(纵向、扭转)频率应高于1.15ω0，且界面连接刚度要大于估算出的基础模块等效静刚度。

(2)对于附加模块研制部门：附加模块在底部连接了刚度特性与估算所得基础模块等效静刚度相同的无质量弹性单元后，一阶横向弯曲(纵向、扭转)频率应高于1.15ω0，且附加模块的质量特性应小于估算值。

本文结合悬臂梁理论提出了一种串联舱段卫星总体频率指标的分解方法，对于一阶横向弯曲、一阶纵向和一阶扭转频率都有较高的精度。该方法可以有效降低设计代价和设计风险，提高载重比，为合理设计卫星结构和分配质量提供关键性支持。存在不足的地方是该方法的普适性仍需要进一步的理论研究和证明，望在今后的研究中能够有所突破。