中高轨卫星海洋成像图像几何定位精度提升方法
2020-05-15刘晓磊董小萌潘忠石张过宋鹏飞
刘晓磊 董小萌 潘忠石 张过 宋鹏飞
(1 北京空间飞行器总体设计部,北京 100094)(2 武汉大学 测绘遥感信息工程国家重点实验室,武汉 430079)
遥感卫星发射过程中的应力释放及卫星在轨运行的物理环境变化,均会引起几何定位参数(载荷安装、CCD焦面排列及镜头畸变等参数)的改变;另外,卫星的姿态轨道测量系统等也往往存在系统性偏差,这些均会降低卫星几何定位精度。目前,采用在轨几何检校技术是提升遥感卫星图像几何定位精度的一种有效手段,如国外的斯波特-5(SPOT-5)、“艾科诺斯”(IKONOS)、“地球之眼”(GeoEye)、世界观测-1(WorldView-1)和WorldView-2等,采用在轨几何检校后,无控制点定位精度能实现10 m以内[1-8]。我国遥感卫星也采用在轨几何检校技术,典型方法包括偏移矩阵[9]、姿态系统误差检校[10-11]等,目前我国资源三号卫星可实现无控制点定位精度优于25 m[12-13]。上述国内外卫星主要是低轨遥感卫星,综合来讲,可实现较高的定位精度。然而,随着中高轨遥感卫星的不断发展,特别是海洋成像时,在无控制点的情况下提升卫星图像几何定位精度具有很强的应用需求,且国内外目前尚未见中高轨卫星海洋成像时图像几何定位提升技术研究的相关报道,这是一个值得研究的问题。
本文提出一种针对中高轨卫星海洋成像的无控点定位精度提升方法,利用中高轨卫星成像范围大,配合姿态机动,在短时间内寻找有特征点的区域,通过卫星图像与高精度控制图像进行匹配,寻找控制点,求解偏置矩阵,并将该区域的偏置矩阵补偿到海洋地区,达到提升图像定位精度的目的。最后,通过成像仿真及检校仿真试验,利用快速机动获取的有控制点的检校数据对无控制点数据进行检校,证明了该方法用于中高轨卫星海洋成像图像几何定位精度提升的可行性。
1 海洋成像无控制点定位精度提升方法
1.1 总体思路
中高轨卫星对海洋成像时,很难在影像上找到特征控制点,因此中高轨卫星提升几何定位精度需要利用在轨检校技术将成像系统误差消除。相对于低轨卫星来讲,中高轨卫星成像范围大,配合姿态快速机动,能够在短时间内寻找到有特征点的区域,而卫星在短时间内数次成像中系统误差较为稳定,则可以利用有特征点的影像求解偏置矩阵,并应用到海洋影像中,以提升海洋成像无控制点定位精度。本文方法实现过程见图1,总体思路如下。
(1)卫星下传的海洋影像(待补偿影像)周围没有特征区域,卫星执行姿态机动命令,直到影像上有控制区域(一般要求至少有1个明显控制点,如海岛、海岸线等)为止,此时的影像叫做检校影像。
(2)利用检校影像的姿态、轨道、成像时间等辅助信息,配合高精度控制数据,对控制数据进行重采样,生成一幅与检校影像相同大小的影像(简称模拟影像)。方法详见1.2节。
(3)针对检校影像与模拟影像,采用满足亚像素级的高精度配准算法进行列等间隔配准,在检校影像上获取控制点。方法详见1.3节。
(4)利用配准获取的控制点解求偏置矩阵。方法详见1.4节。
(5)将得到的偏置矩阵Ru应用到海洋影像(待补偿影像)中,补偿载荷安装误差及姿态、轨道系统误差,提高中高轨卫星海洋图像几何定位精度。方法详见1.5节。

图1 方法实现过程Fig.1 Method process
1.2 模拟影像生成
中高轨卫星采用姿态机动方法寻找周围有控制区域的地方进行成像,这就要求在能够找到控制点的区域(如海岛)都要有控制数据。鉴于这种应用,本文采用全球15 m左右精度的陆地卫星-6(Landsat-6)的增强型专题绘图仪(ETM)数据及全球6 m左右精度的雷达测绘高精度数字高程模型(SRTM-DEM)/“土”(Terra)卫星先进热辐射与反射辐射计(ASTER)的数字高程模型(DEM)数据作为控制数据,支撑中高轨卫星进行在轨几何检校。
生成模拟影像时,针对检校与高精度数字正射影像图(DOM)分辨率差异,利用检校影像的辅助姿态、轨道、影像行扫描时间文件、高精度DEM影像,构建严密几何成像模型,对高精度DOM影像进行重采样,从而生成一幅与检校影像相同大小的模拟影像,具体步骤如下。
(1)利用实验室测量的内方位元素和姿态与轨道数据,结合高精度DEM影像,构建严密几何成像模型。
(2)对模拟影像上像素点(行列坐标为(s,l),利用严密几何模型建立地面坐标点在WGS84坐标系下的坐标与模拟影像像素点坐标的对应关系(即(X,Y,Z)WGS84=T(s,l)),通过地面点在WGS84坐标系下的坐标(X,Y,Z)WGS84到(Llat,Llon,h)(纬度,经度,高程),再到DOM上的坐标点(E,N)refDOM(E和N分别为DOM上的行坐标点和列坐标点)的变换过程,从WGS84坐标系变换到高精度DOM坐标系下。
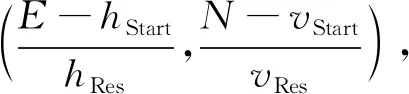
(4)重复步骤(1)~(3),直至生成一幅与检校影像相同大小的模拟影像。
1.3 获取检校影像控制点
利用检校影像与模拟影像,采用满足亚像素级的高精度配准算法进行列等间隔配准,获取控制点,步骤如下。
(1)根据检校影像的CCD阵列大小,确定配准列间隔。假定检校影像大小为ws·hs,(ws和hs分别为检校影像的列数和行数)取列间隔n,则配准将在检校影像的i·n列上进行(i=1,2,3,…,且i·n≤ws)。
(2)针对检校影像的i个配准列i·n,对该列下的hs个影像点逐一与模拟影像配准,保留满足配准精度的所有点;对检校影像选定的所有配准列进行此操作。
(4)利用1.2节步骤(1)中构建的模拟影像严密几何成像模型,计算得到各配准点对模拟影像像点的地面坐标(Llat,Llon,h),从而得到检校影像控制点地面坐标(s′,l′,Llat,Llon,h),(s′,l′)与(s,l)为配准点对。
1.4 求解偏置矩阵
利用配准获取的控制点求解偏置矩阵,偏置矩阵Ru的求解方法一般按摄影测量中后方交会方法进行,见式(1)。
(1)

严密几何成像模型可变换为
(2)
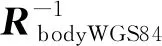
令
(3)
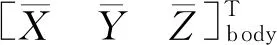
展开有
(4)
式中:fx,fy为检校后的2个方向偏置角与检校前的差值。
列出误差方程为
V=BX-l
(5)
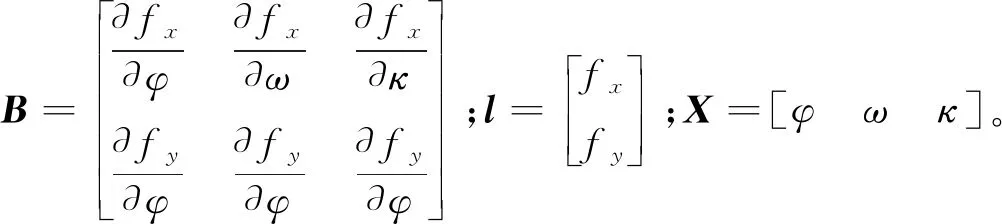
利用最小二乘原理X=(BTB)-1BTl,可计算出偏置矩阵3个角元素φ,ω,κ,从而求解出偏置矩阵Ru。
1.5 检校补偿
首先,构建中高轨卫星外方位元素检校模型。影响定位精度的外方位元素主要包括轨道测量误差、姿态测量误差及载荷安装误差。依据对几何定位精度的影响特性,载荷安装误差可以等效于姿态测量误差。轨道测量误差虽然对几何定位精度的影响特性与姿态误差有所差异,但是两者可以依据一定的几何关系进行等效处理。如图2所示,S表示当前时刻卫星成像的真实位置,S′为卫星测量位置,P和P′分别为真实地面点位置和地面点测量位置,DX为卫星轨道位置偏移误差,则易看出,轨道误差DX可以等效成姿态误差dθ(θ真实光线与测量光线间的夹角),两者对几何定位精度影响一致。以轨道测量误差为例,其对几何定位精度的影响表现为平移误差,影响特性虽与姿态误差有所差异,但是两者可以依据一定的几何关系进行等效处理,如图3所示。
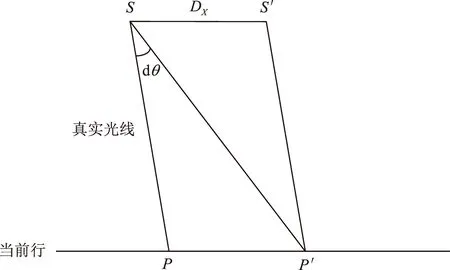
图2 线元素和角元素等效关系Fig.2 Equivalent relationship between line and angle elements

图3 线平移误差与角误差等效关系
在图3(a)中,ΔZ为轨道径向误差,ω0为线阵CCD成像光线的滚动角(包括卫星侧摆角及CCD探元视场角),则引起的径向定位误差ΔP为
ΔP=ΔZtanω
(6)
卫星无侧摆正视成像时,当相机视场较小且定轨精度较高时,ΔZ引起的几何定位误差可以忽略;当卫星大侧摆成像时,式(6)对ω求偏导有
d(ΔP)=ΔZsec2ωdω
(7)
根据式(7),考虑当ΔZ<5 cm,ω≤32°,dω≤5.6°时,ΔZ对不同视场角探元引起的几何定位误差的差异小于0.06 m,即在大侧摆成像条件下,ΔZ引起的误差为平移误差,可等效为相应方向轨道误差。
在图3(b)中,假设卫星成像视场角为ω(不同探元ω不同),滚动角误差为Δω,则引起的垂直轨道定位误差ΔY为
ΔY=Htanω-Htan(ω+Δω)
(8)
式中:H为轨道高度。
对ω微分有
d(ΔY)=H[tan2ω-tan2(ω+Δω)]dω
(9)
在最坏情况下,滚动角误差对各个不同探元造成的几何定位误差的差异不超过0.5个像素,可以认为滚动角误差对各探元影响一致,从而图3(b)中滚动角误差与垂直轨道方向轨道误差等效。因此,轨道误差可以等效为姿态误差。图3(c)的情况与图3(b)情况类似。
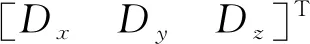
(10)

有了几何检校模型,利用第1.4节得到的偏置矩阵Ru,应用到海洋影像(待补偿影像)中,补偿载荷安装误差及姿态、轨道系统误差,即可提高中高轨卫星海洋成像图像几何定位精度。
2 仿真试验
为了验证本文方法的可行性,进行了相应的仿真试验,试验的全部流程与上述方法保持一致。由于最终的检校精度定量评价需要有控制点,本文仿真试验中没有采用海洋区域,而是将待补偿图像设在陆地,以便定量评估,但方法对海洋同样适用。
仿真试验的输入数据包括:①含误差的轨道数据;②含误差的姿态数据;③WGS84与J2000坐标转换的转换矩阵文件;④成像时间数据;⑤模拟影像。利用仿真软件,仿真了2套数据,分别位于河南嵩山检校场和太原区域。利用河南嵩山检校场数据进行在轨几何检校,将检校参数补偿到太原区域,对太原区域的定位精度进行评估,检验提升方法的有效性。误差仿真参数设置如表1所示。
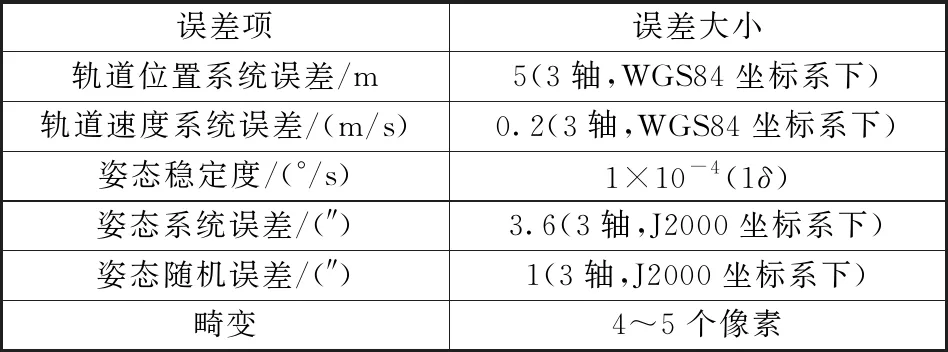
表1 误差仿真参数设置
采用本文方法,得到偏置补偿矩阵,利用偏置补偿矩阵对嵩山场景进行检校,得到检校前后的定位精度,结果如表2所示。可见,在进行外方位元素检校前,直接利用星上下传的原始数据的无控定位精度为137.1个像素,直接定位精度比较差;在通过本文方法进行偏置矩阵求解之后,将得到的偏置矩阵反代入嵩山场景中,得到平面精度为1.6个像素,自我补偿精度比较高,剩下的1个多像素的误差来源于影像内部精度的不一致。
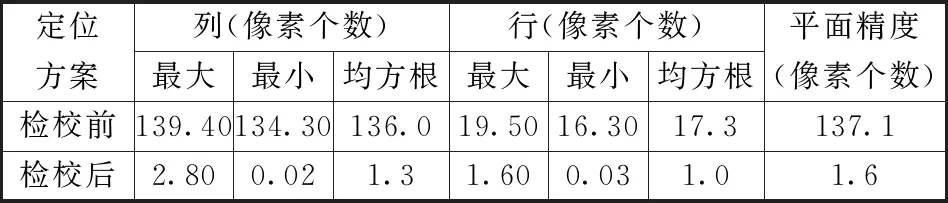
表2 嵩山场景检校前后定位精度统计
在得到偏置补偿矩阵后,将其用于太原区域的补偿,通过补偿精度来评价本文方法的可行性。表3为太原场景补偿前后的定位精度,偏置补偿前的直接定位精度为118.3个像素,经过偏置补偿后,定位精度提高到37.8个像素。补偿后场景和检校后场景的定位精度有差异,是因为检校后场景和补偿后场景所在的姿态轨道随机误差不一样,且偏置补偿的仅仅为卫星的稳定安装部分。

表3 太原场景补偿前后定位精度统计
通过仿真结果可以看出:利用检校后场景的偏置矩阵补偿实际场景(太原场景),可以提升无控制点的定位精度。在仿真试验中,实际场景的无控制点定位精度从118.3个像素提高到37.8个像素,定位精度显著提升,证明了中高轨卫星海洋成像时,可利用中高轨可视范围宽的特点,配合姿态机动获取临近有控制点数据,并进行海洋区域图像检校,从而提升中高轨卫星海洋成像无控制点几何定位精度。
3 结束语
本文基于中高轨卫星对海洋成像时无控制点情况下定位精度提升需求,提出了一种利用中高轨卫星成像范围大,配合姿态机动,在短时间内寻找有特征点的区域成像并求解偏置矩阵,应用到海洋区域的检校方法。在寻找控制点时,本文基于全球高精度控制数据,配合机动成像的姿态轨道辅助数据,重采样控制数据形成模拟影像,并通过模拟影像与检校影像高精度配准,寻找检校影像高精度控制点,为求解相对准确的偏置矩阵提供基础。经过仿真验证,本文方法对海洋成像的无控制点定位精度可提升3倍,可应用于中髙轨卫星对海面成像任务时对应的图像处理,支持生成高精度几何定位图像数据。
