高速列车受电弓杆件减阻降噪研究分析

2020-05-14徐志龙刘海涛王超文陈永华

华东交通大学学报 2020年2期

徐志龙，刘海涛，王超文，陈永华

（1.华东交通大学机电与车辆工程学院，江西南昌330013；2.杭州地铁集团有限责任公司运营分公司，浙江杭州310017）

近年来随着高速列车的快速发展以及都市化进程的加快，人们对高速列车速度的追求也越来越高。在列车速度达到250 km/h 时，列车与空气相互作用引起的气动噪声将首次超过轮轨振动噪声，是制约列车速度的重要因素之一[1]。蔡国华等[2]发现，当列车速度达到200 km/h 时,大约有70%的功率用于克服空气阻力，并且随着车速的进一步提高，不仅空气阻力急剧增加，受电弓还会与输电导线之间产生极为严重的气动接触压力和气动噪声，影响受电弓质量。列车的气动噪声主要包括列车车头，车体转向架，受电弓等与空气相互作用所产生的脉动压力变化引起的噪声。受电弓作为列车顶部的重要受流装置，其复杂的结构形式对高速列车的空气动力学性能影响很大，因此对高速列车受电弓杆件的优化具有重要意义。

Nishimura 等[3]在圆柱杆件表面粘贴绒毛织物，结果发现绒毛织物虽然能略微增加气流湍流流动的阻力，但能有效地降低圆柱杆件的气动噪声以及降低杆件表面的脉动压力。King 等[4]对受电弓杆件的不同截面形状（包括圆形，正方形，矩形和椭圆形）进行了气动噪声测试，得出椭圆截面杆件的气动噪声较其它截面杆件的气动噪声更低。近年来，仿生学的发展为机械结构的减阻降噪研究带来了新的契机，提出一种非光滑结构的减阻降噪新思路，就是把自然界中具备低阻力，低噪声的典型生物的体表形态特征应用到实际工程中来[5]。 Hersh[6]，李典[7]，吕建民[8]和葛长江[9]等受到鸮翼前缘锯齿结构的启发，均验证了基于仿生的鸮翼锯齿结构能有效地达到减阻降噪的目的。石磊等[10]利用仿生学原理设计出了锯齿形，V 型凹环型和波浪形这三种结构，与光滑的圆柱杆件相比，这三种非光滑结构的杆件表面的脉动压力均有明显的减弱。汪久根[11]提出一种雪花表面织构的非光滑结构，通过在雪花织构内部产生二次涡，大大降低了与空气相互作用产生的摩擦噪声，而且进一步研究发现不同尺度的表面织构与圆坑交叉耦合还要优于单一表面织构。 NASA 兰利研究中心的Walsh 等[12-14]受到鲨鱼表面微沟槽的启发，设计了多种沟槽结构，通过风洞实验测试，发现V 型沟槽具有良好的减阻效果，最高减阻率达到25%。

海螺，贝壳等海洋生物为了抵御海水的冲蚀以保持自身的稳定，其外壳表面进化出凸陷螺纹线。基于其外壳表面微结构启示，设计出凹槽螺纹型和凸陷螺纹型两种不同结构的杆件。在速度为350 km/h 的空气域中，通过定量比较螺距和螺纹参数下非光滑结构杆件的气动阻力和气动噪声，来探求非光滑杆件的减阻降噪机理，为新型受电弓的减阻降噪提供借鉴和指导。

1 计算理论及方法

1.1 空气动力学理论基础

空气动力学为流体力学的一个分支，所以在对高速列车受电弓杆件周围流场进行数值仿真时，数值模拟的控制方程采用三维的N-S 方程，笛卡尔坐标系(x1，x2，x3)，定义速度分量(u1，u2，u3)，完整的三维N-S 方程守恒形式如下

式（1）中U，F， fv的表达式如下

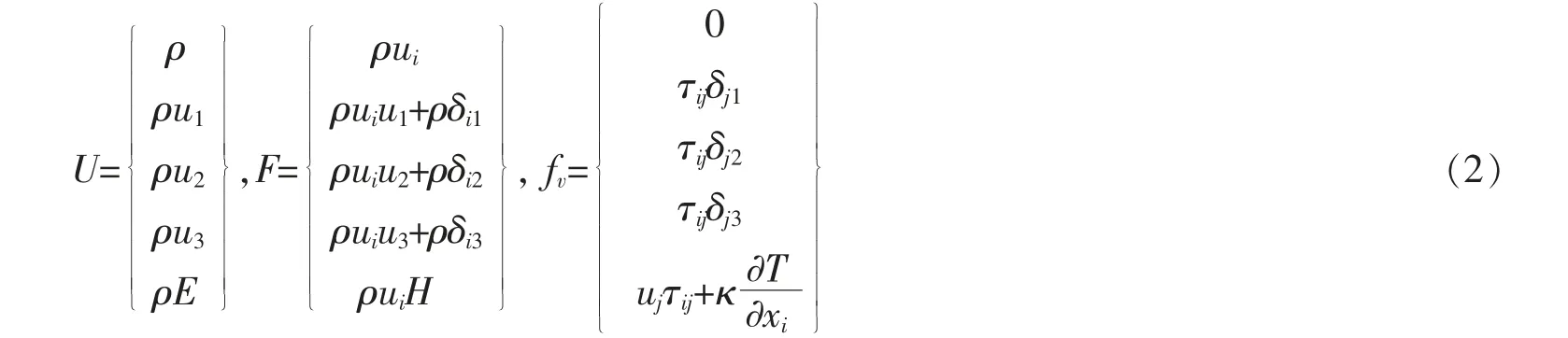
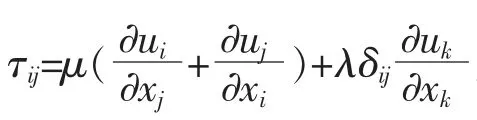
1.2 气动声学基础

气动噪声是由于气体与固体或者气体与气体介质之间的冲击、碰撞等相互作用而产生的气流压力波动所导致的。根据声学相似理论以及气动声学产生的机制，流场中的声源可以分为：单极子声源、偶极子声源以及四极子声源。其中偶极子声源也称为流体动力声，因为偶极子声源没有质量和热量的变化（两边相互抵消），但需要外加振动力。偶极子声源是流体中存在障碍物时，流体与流体之间出现不稳定的反作用力而形成的。

高速列车受电弓产生的气动噪声属于偶极子声源的范畴，在对高速列车受电弓杆件进行气动噪声计算时，采用基于Proudman 理论的宽频带噪声模型进行计算机仿真。 Proudman 方程由Proudman 于1952 年导出，用于求解高雷诺数、低马赫数及各项同性湍流流动中的气动噪声。本研究的计算对象满足该模型的假定条件，模型中声功率计算公式如下

式中：u 为湍流速度；l 为湍流特征尺度；c0为声速；α 为模型常数。ρ0对于紊流脉动动能K 和紊流脉动动能的耗散率ε，式（3）可以改写为下式

气动噪声声功率级如下

式中：Pref为10－12W/m3。

2 仿真模型的建立

对受电弓杆件进行仿真分析时，考虑计算机仿真所消耗内存资源较大，故选取受电弓的一段杆件进行三维流体仿真分析，杆件的尺寸与受电弓杆件的常规尺寸相近，直径为60 mm，高度为240 mm。为了使仿真结果更加接近实际情况，需建立一个与受电弓杆件模型不产生干涉的空气域模型，所建立的空气域为900 mm×500 mm×240 mm，如图1 所示。

计算域模型建立完成并且网格划分质量符合要求之后，在Fluent 软件中进行三维流体仿真。本研究是基于稳态仿真计算，且流体介质为标准气压下的空气介质，采用Reynold 平均模拟的标准k-ε 湍流模型进行稳态计算。在实际的环境中，真实的流体都具有不同程度的压缩性，而空气的压缩性更为明显。在不可压缩流体介质流动中，流动的参数通常只是速度和压强，但是在可压缩流体介质中，另外还增加了密度和温度两个变量，导致流场控制方程的数量增多以及解方程的复杂程度也加大。但是当马赫数比较小的时候，就可以忽略流体密度变化的影响，就可划分到不可压缩流动的范畴。

仿真流体运动中流动速度350 km/h，其马赫数约为0.286（小于0.3），因此不属于可压缩的范畴。而流场中边界条件的设置决定了流场仿真控制方程解的唯一性，又叫做流场的定解条件。对于边界条件设置是假设受电弓模型不动，空气以一定的速度在空气域模型中水平流动，利用这种方法来模拟高速列车所处的实际环境，边界条件设置如表1 所示。

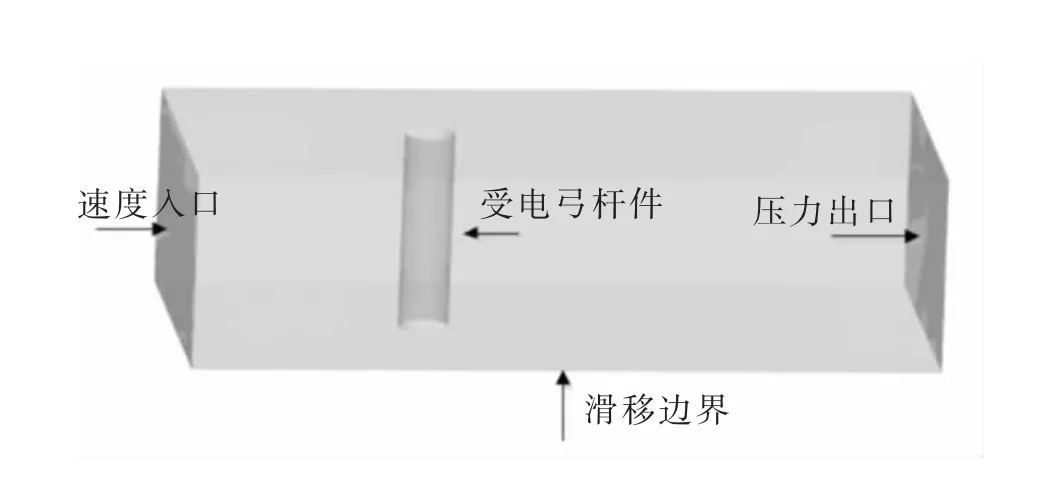
图1 仿真几何模型Fig.1 Simulation geometry model

3 杆件的仿生设计

受到自然界中海螺，贝壳等海洋生物类似螺纹线外壳启发，通过仿生学思想,对高速列车受电弓杆件提出一种非光滑表面结构设计。本设计将高速列车受电弓杆件处理成一种螺纹型非光滑表面结构，即凹槽螺纹型和凸槽螺纹型两种不同类型的杆件，如图2 所示。

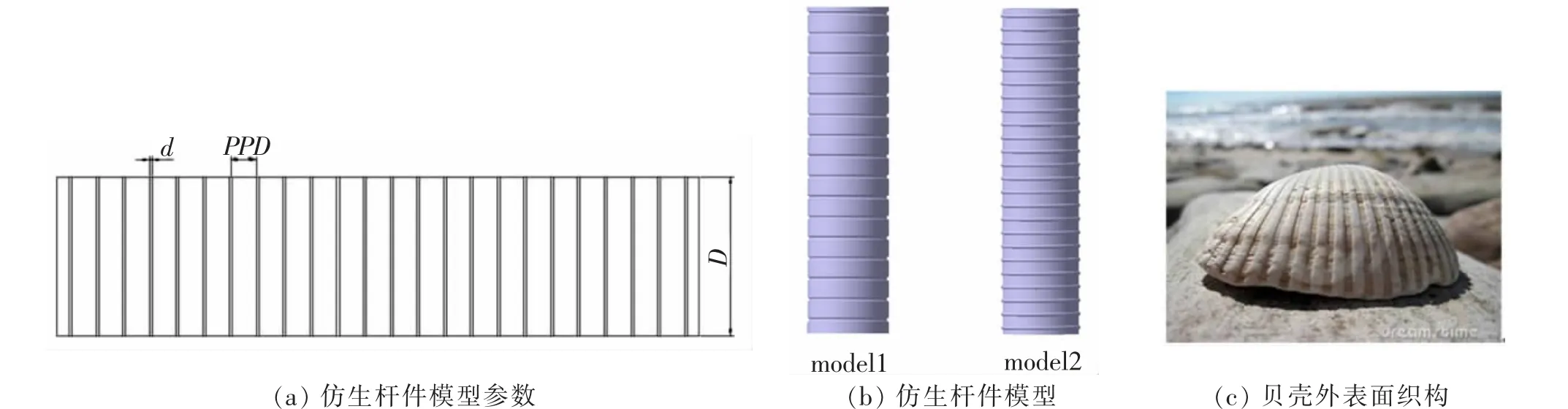
图2 仿生杆件模型Fig.2 Bionic bar model

其中model1 带有凹槽螺纹型非光滑表面，model2 带有凸陷螺纹型非光滑表面。为了更深层次地探求螺纹型非光滑表面结构气动阻力和气动噪声的影响，分别对这两种类型杆件的螺距PPD 与螺纹直径D 进行不同规格参数化分析，具体参数如表2。

4 仿真结果分析

采用ANSYS Fluent 进行三维流体仿真，基于标准k-ε 湍流模型和宽频带噪声模型，在速度为350 km/h 的环境下，所得到的螺纹型各类型杆件不同参数下的气动阻力和气动噪声值如图3所示。

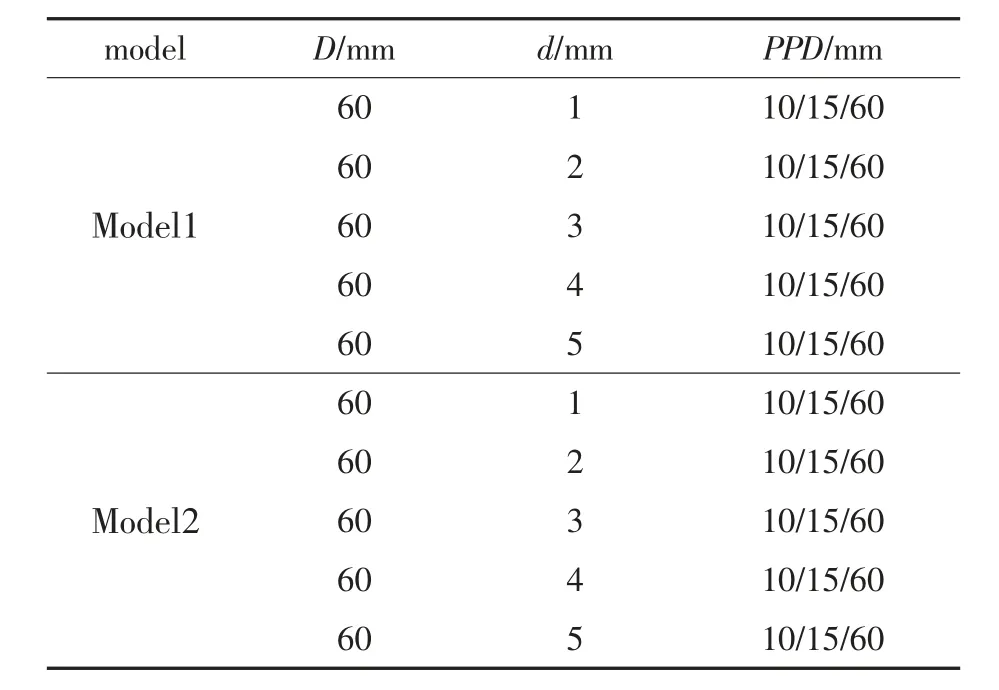
表2 螺纹型杆件各参数Tab.2 Parameters of threaded bar

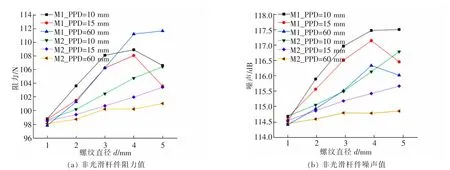
图3 非光滑杆件阻力和噪声值Fig.3 Drag and noise of non-smooth bars

其中M1_PPD=10 表示螺距PPD=10 mm 不同螺纹直径的凹槽螺纹型杆件，M2_PPD=10 表示螺距PPD=10 mm 不同螺纹直径的凸陷螺纹型杆件。从图中可以看出，螺距PPD=60 mm，螺纹直径d=1 mm 的凹槽螺纹型杆件（M1_PPD=60）所产生的气动阻力和气动噪声均最小，而且凸陷螺纹型杆件普遍要比凹槽螺纹型杆件的气动阻力和气动噪声要明显小很多。为了研究其内部机理，将PPD=10 mm，d=1 mm 的凹槽螺纹型杆件与同尺寸的传统光滑受电弓杆件所仿真的速度流场云图和声功率云图绘制出来进行比较如图4 和图5 所示。

图4 速度流场分布Fig.4 Velocity flow distributions

图5 声动噪声云图Fig.5 Sound-power contour

从图4 中可以看出，传统的光滑杆件A 相对于螺距PPD=60 mm，螺纹直径d=1 mm 的凹槽螺纹型杆件尾部区域具有更大的涡流区，并且涡流在圆柱杆件的边界层上发生分离，分离时形成的漩涡被主流带走，在物体后部形成尾流区，边界层分离后的流动很复杂，由于尾涡中含有大量紊乱的漩涡，消耗大量的动能，这对流动来说是一种阻力作用，这也是模型B 中的螺纹型非光滑表面结构破坏了尾流漩涡的发展导致阻力减小的关键原因之一。结合图5 所示，模型B 中的凹槽螺纹型非光滑表面使得边界层的分离点更延后，根据涡声理论，涡流是气动噪声产生的直接原因，模型B 中尾流区域的减小使得气动噪声的范围和幅值都要显著低于传统的光滑杆件模型A，这也是仿生结构减阻降噪的关键机理所在。