考虑悬臂结构转动的开启桥桥面铺装动响应分析

魏 鹏，刘 云，匡 伊

（河海大学道路与铁道工程研究所，江苏 南京210098）

立转式开启桥具有开启快速便捷、开启时航道上方无净空限制等优点，国内外越来越多的地区开始规划和设计建设开启桥。 但是立转式开启桥桥面铺装不仅要承受行车荷载的作用，还要满足桥梁开启和闭合过程中对于铺装体系层间粘结性能的要求。 张磊等[1]通过有限元模拟分析桥梁开启阶段不同开启速度和铺装结构模量对铺装层应力响应的影响，刘云等[2]采用有限单元法计算比较了开启桥在通车运营和通航开启两种状态下铺装层应力的变化，并分析铺装模量对层间剪应力的影响。 现有的研究是通过建立不包括转轴的开启桥简化仿真模型，模拟分析开启速度、铺装材料等因素对开启桥启闭过程中铺装层的动力响应，开启桥的转动开启是通过转轴的转动实现的，为了实现桥梁的开启，简化模型将转轴约束到一个点，在这一个点处施加速度实现转动[3]。 简化的模型并不能还原桥梁整体结构在开启中对铺装瞬态动应力的影响，而且开启桥与大跨径悬索桥、斜拉桥相比，跨径不足百米，精细化的模型更能准确反映应力的变化情况；因此为了进一步分析研究悬臂桥梁开启时桥面铺装的响应问题，本文选用ANSYS 有限元软件，建立包含转轴、套环箱室等精细构件的开启桥模型，通过在转轴实体上施加转动角速度来实现桥梁开启，将转轴转动纳入到整体桥梁结构中，模拟在工程实际的开启方案下，桥面铺装的主要力学控制指标在转动开启过程中的动态力学响应，为开启桥桥面铺装的设计与施工提供参考。

1 工程概况

天津响螺湾海河开启桥全长约1 066 m，整体结构由人行道、枢轴、箱梁、横梁、U 型梁及钢桥面板等构件组成，采用双叶立转式钢结构悬臂梁开启方式。 钢结构开启桥悬臂部分主梁采用变截面钢箱梁，双箱单室。 开启桥采用双叶立转式开启，开启桥段结构对称，单叶开启段跨径38 m，主梁宽为20 m，图1 所示为主梁正截面图。 开启桥钢桥面铺装行车道采用单层铺装方案，铺装层厚度为3.0 cm 的轻质国产环氧沥青混凝土[4-7]。 在整体计算中，假设钢结构各个不同的构件材料均为理想材料,符合胡克定律。

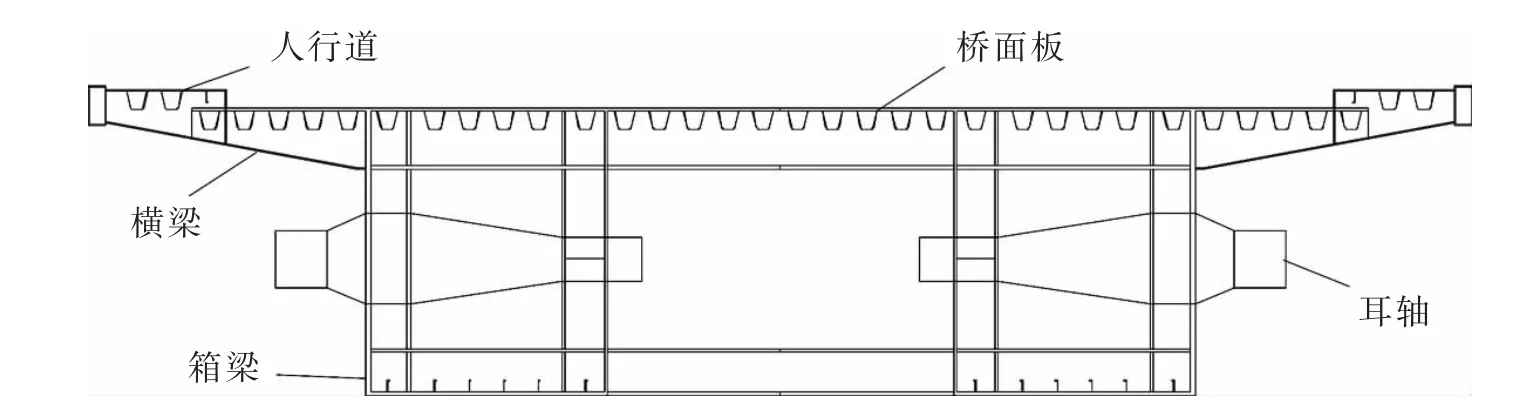
图1 开启跨桥体主梁典型剖面图Fig.1 Typical section of the main girder of the open span bridge

2 有限元模型的建立

2.1 开启桥有限元模型建立

为了精确模拟铺装的力学行为，便于后期查看开启桥不同部位在不同分析情况下的变形情况，本文采用ANSYS 软件中的APDL 语言参数化建立1/4 的开启桥模型[8]，通过命令流的方式将整体结构划分为多个局部构件分开建模，单独建立转轴实体以及正交异性钢桥面板铺装体系复合结构。 开启桥1/4 正交异性钢桥面板复合铺装体系结构模型根据已有研究的相关几何及物理参数建立，各项参数如表1 所示。 几何模型建立之后，可在ANSYS 中局部赋予不同组件的材料属性。

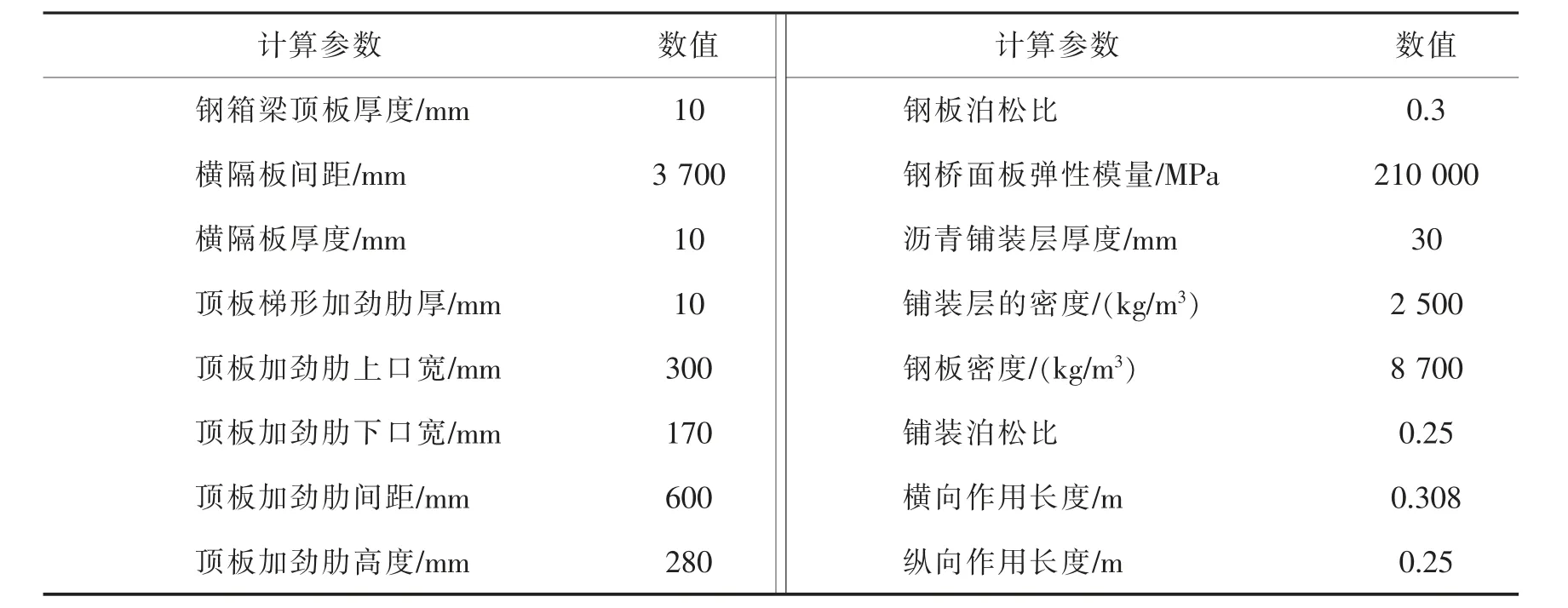
表1 开启桥模型几何及物理参数Tab.1 Open bridge model geometry and physical parameters

根据有限元方法的基本原理， 利用有限元进行数值计算时网格划分的密度对计算结果有显著的影响。网格越密，计算精度越高，但所需的计算时间也越长。 为了提高有限元计算的精度和效率，考虑到主要分析转轴转动以及铺装结构的受力变化情况， 钢桥面板以及桥梁整体箱室等部分采用0.5 的网格尺寸划分较为稀疏，转轴、套环实体及铺装层网格划分较细密，网格尺寸为0.1。 整体模型及部分组件划分后的网格模型图如图2 所示。

图2 开启桥模型图Fig.2 Open bridge model diagram

2.2 正交异性钢桥面铺装体系复合结构的建立

由于桥面铺装较容易出现开裂、剥落等不同形式的破坏， 而ANSYS 中的solid185 单元具有拉裂与压碎的可能性，可有效地模拟沥青混合料铺装层的受力情况。 在钢桥面板建立的过程中，纵向加劲肋、横隔板、主梁腹板与钢桥面板构成了一个完整的复合结构，复合铺装的建模较为简单，在钢桥面板顶部建立相应厚度的矩形板即可模拟铺装结构。 网格按之前所述划分，建成后的钢桥面板铺装体系如图3 所示。

最后通过“搭接”命令将分组件建立的正交异性钢桥面铺装体系结构、转轴与套环实体结构以及桥梁箱室板壳结构的精细有限元模型形成一个连续的整体，为后续不同工况下的模拟提供一个更符合工程实际的有限元模型。

图3 正交异性钢桥面板铺装复合结构图Fig.3 Composite structure diagram of orthotropic steel deck paving

2.3 边界条件及接触条件

开启桥的转轴与桥墩之间采用的连接方式是铰支，支座为球形滚轴支撑，通过楔套安置于轴上，一个固定在楔套内，另一个则在套筒内滑动，从而使得开启桥具有一定的伸缩范围。 在建模过程中，将转轴与桥墩连接的边界条件简化为X，Y，Z 方向的平动自由度，即转轴实体两端中心点处完全固结。 铺装层和钢桥面板间不发生水平移动，允许竖向位移，即为UX=UZ=0。 结合开启桥的有限元精细模型及后续运算的需求，在转轴与套环实体接触处、钢桥面板与铺装层的接触处均设立了柔体-柔体面面接触。

3 开启桥转动开启中铺装层动力响应分析

3.1 开启方案及阻尼系数选取

桥梁悬臂结构的开启及闭合是通过有限元软件在转轴实体上施加转动角速度来实现的，选取开启总时长170 s， 开启桥最大开启角度为85°， 选取变速开启方案， 最大开启角速度为0.009 566 rad/s，设定35 个时间步长进行瞬态动力运算，具体方案如表2 所示。

正交异性铺装体系进行开启动力响应模拟时采用Rayleigh 阻尼[9-12]，本文动力分析模型的结构阻尼比取0.01[13-14]，可得阻尼常数α 和β 分别为0.026 和0.003 8。

3.2 开启阶段铺装层应力分析

根据目前的相关研究可知，铺装层最大拉应力是钢桥面铺装抗裂设计的一个重要指标，另外，铺装体系与钢板之间的粘结破坏是钢桥面铺装最典型的破坏形式之一；因此选取层间剪应力与拉应力作为立转式开启桥钢桥面铺装的主要力学控制指标，研究这两个控制指标在变速开启方案下的动力响应对于开启桥的设计十分必要。

对于开启角度，此次针对性选取30°，50°，70°，85°共4 个角度下铺装体系的应力分布进行具体分析，以层间最大剪应力和横向最大拉应力作为衡量指标，总结出在不同角度时铺装结构的应力变化情况，开启桥1/4 模型在4 个角度时整个桥面板铺装体系等效应力云图见图4 所示。

从图4 可以看出，在转动过程中，转轴正上方铺装体系的应力会出现不同程度集中效应，且在开启过程中转轴中心线上方的应力值也会相应较大，不同开启角度的层间剪应力峰值和铺装拉应力峰值出现的位置相近，都在桥面板架构的自由端位置。

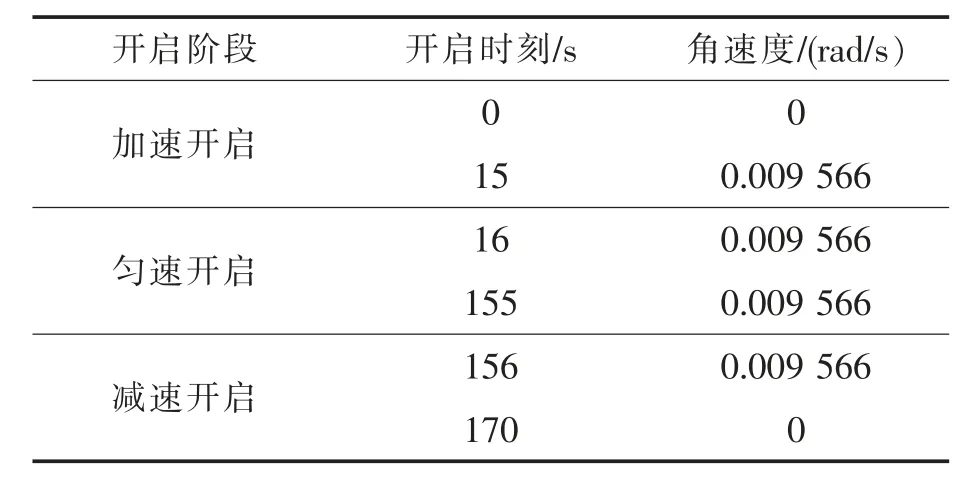
表2 开启桥开启方案Tab.2 Open scheme of the bascule bridge

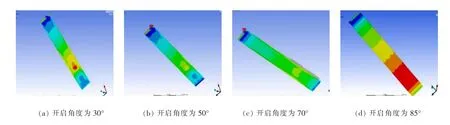
图4 开启桥1/4 模型铺装体系等效应力云图Fig.4 Equivalent stress nephogram of 1/4 model pavement system of the bascule bridge

1） 层间最大剪应力分布规律。 图5 是开启桥开启过程中自由端位置层间最大剪应力随着开启时间的变化图，从图中看出，在开启的初期，即大约0 到10 个时间步期内，此时开启桥正值加速开启向匀速开启转换的阶段，发现层间剪应力增长缓慢，最大剪应力在0.35 MPa 浮动，说明此时开启角度较低，加速度较慢，层间剪应力响应不明显；随着速度增加，开启角度增大，开启桥层间剪应力呈现线性增长趋势，此时层间剪应力受角度和速度影响显著；在接近完全开启时，即25 到35 的时间步内，开启桥逐渐达到最大开启角度，并减速开启，在最大角度85°时剪应力达到最大值0.735 MPa，此阶段应力增长趋势较缓。

从图6 可以发现，在开启过程中，层间最大剪应力随开启角度呈近线性增长，在最大开启角度85°时剪应力达到峰值0.735 MPa，说明层间最大剪应力受角度变化影响明显，角度越大，产生的层间剪切力越大。

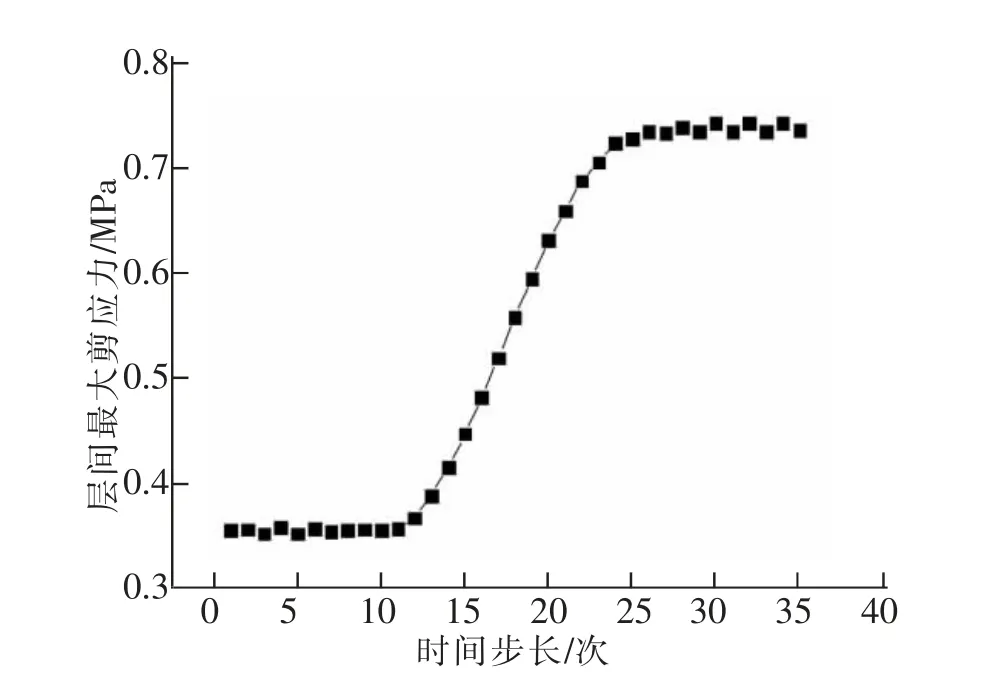
图5 层间最大剪应力随开启时间变化曲线图Fig.5 Graph of maximum shear stress between layers changing with opening time

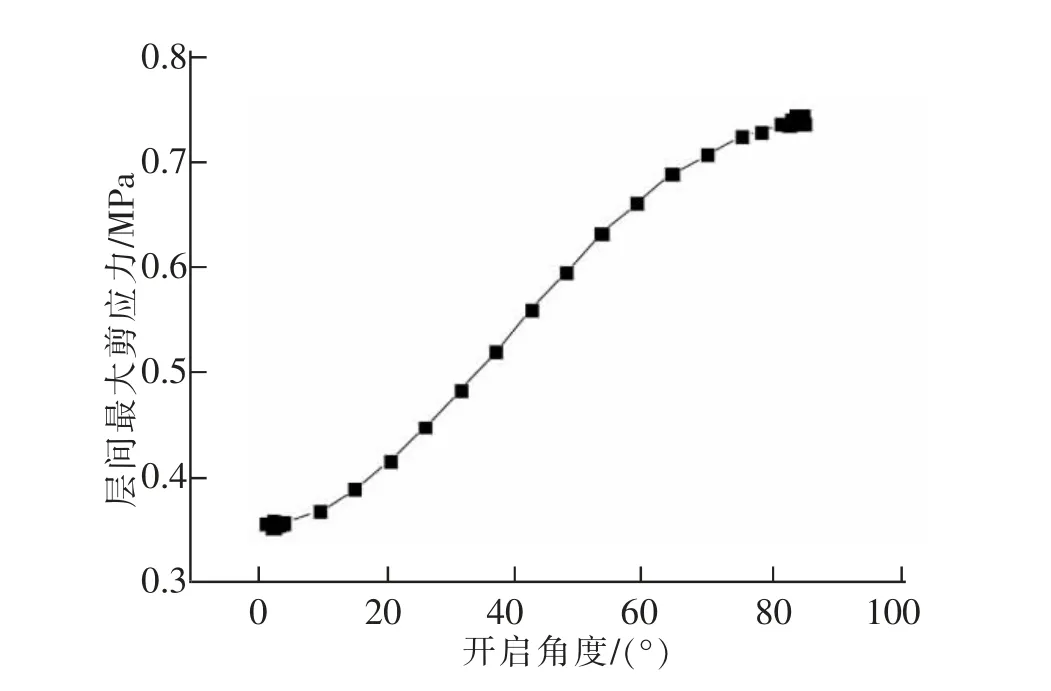
图6 层间最大剪应力随开启角度变化曲线图Fig.6 Graph of maximum shear stress between layers varying with opening angle

开启过程中4 个角度层间最大剪应力值如表3 所示。

从表3 可以发现，开启角度从30°增长到50°时，层间剪应力增幅在37%左右，增速较快，说明此阶段是开启桥开启过程中剪应力快速增长阶段，受开启速度与角度的影响应力变化明显，在实际工程中尤其要注意监测该阶段铺装的应力情况， 在接近完全开启时增速放缓， 从70°到85°层间剪应力增幅达只有4%。 根据相关研究成果[15]，基于钢桥面铺装层间剪应力设计值，考虑安全系数，建议将开启最大速度保持在0.009 566 rad/s 以内。

表3 4 个不同角度最大剪应力值表 MPaTab.3 Maximum shear stress values at four different angles

2） 铺装最大拉应力分布规律。 图7 和图8 是开启桥自由端位置铺装层最大拉应力随时间和开启角度的变化图，从图中可以发现，铺装层最大拉应力随时间和开启角度的增长趋势与层间剪应力基本一致，但整体的拉应力峰值要高于剪应力，最大拉应力在开启桥达到最大开启角度时达到峰值0.834 MPa。

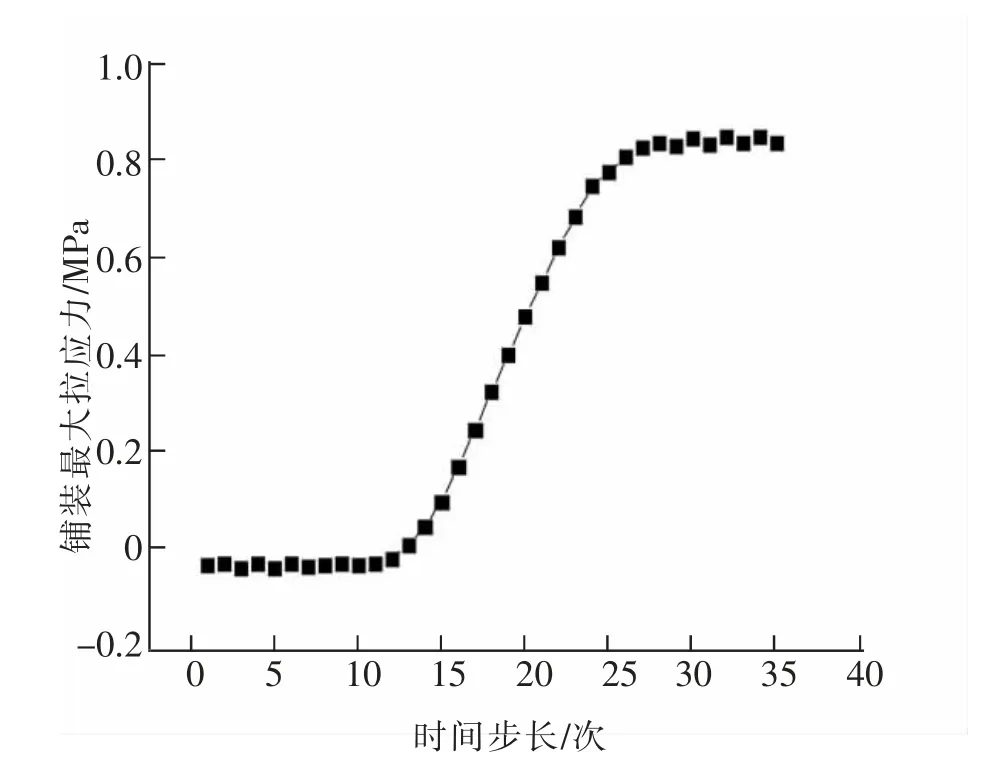
图7 铺装最大拉应力随开启时间变化曲线图Fig.7 Graph of maximum tensile stress of pavement changing with opening time

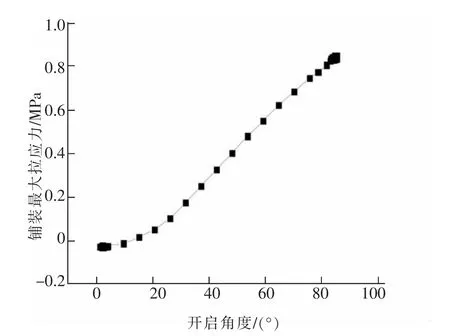
图8 铺装最大拉应力随开启角度变化曲线图Fig.8 Graph of maximum tensile stress of pavement changing with opening angle

从表4 与表3 可以看出，当开启至最大角度85°时，最大拉应力为0.834 MPa，相较于85°层间最大剪应力增长13%左右，同时与层间剪应力的变化幅度相比，可知铺装结构拉应力的变化范围较大，且增长幅度快，所以在开启过程中铺装体系的控制指标应参照拉应力的幅值。

表4 4 个不同角度最大拉应力值表 MPaTab.4 Maximum tensile stress at four different angles

3.3 开启阶段铺装动力响应增加系数

参考现有文献简化转轴实现开启桥开启的建模方法，忽略开启过程中转轴转动对于铺装体系产生的动态响应， 利用有限元模拟开启桥简化模型在开启角度为30°，50°，70°，85°共4 个角度时铺装的静态应力情况，定义铺装动力响应增加系数Dz，计算公式为

式中：σd为精细转轴模型开启过程中铺装的动应力，MPa；σj为简化转轴模型开启阶段铺装的静态应力，MPa。

4 个角度下铺装动力响应增加系数结果见表5 所示。

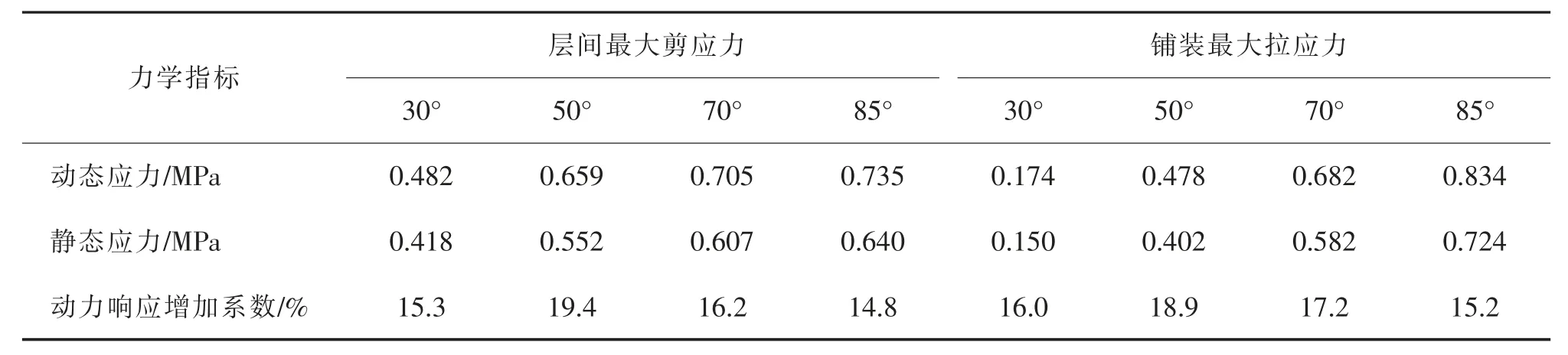
表5 4 个角度下铺装动力响应增加系数Tab.5 Increasing coefficient of pavement dynamic response at four angles

从表5 可以发现，由于考虑转轴转动对铺装的影响，开启桥动态开启过程中铺装的应力响应结果要大于简化转轴模型的静态结果，动力响应增加系数为15%～20%，这是因为建立精细化转轴实体的模型在开启过程中，转轴在箱室中转动时产生的振动传递到整个桥面结构时带来了附加应力，从而导致钢板铺装应力的增大，所以在开启过程中要关注层间的粘结性能，不可忽略转轴实体转动对于铺装产生的动力响应，同时由于考虑转轴实体的模型与工程实际更为符合，所以本文的模拟结果对后期铺装体系的设计优化更具参考价值。

4 结论

1） 在开启桥转动过程中，铺装体系存在明显的应力集中现象，铺装层的力学控制指标为铺装最大拉应力。 铺装层拉应力和层间剪应力均随着开启角度的增大而增加，在开启角度最大时达到峰值，且峰值出现在结构的自由端。 由于变速方案的选择，铺装层应力的峰值随时间增长趋势变化较大，随角度呈缓慢的线性增长趋势。

2） 考虑转轴动态影响的开启桥开启过程中铺装的动力响应结果明显大于简化转轴的静态应力， 且动力响应增加系数为15%～20%；因此建议开启桥设计阶段的复合结构模型要考虑建立精细化转轴。