解决热学U型管问题的 “三步曲”
2020-05-13周胜
周胜

摘 要:从全国卷热学考题出发,分析了学生在解决关于热学U型管问题时容易出现的错误,提出解决此类常见问题的“三步曲”。
关键词:高考;热学;U型管模型
在2019年高考考试大纲关于选修3-3热学的考点中,只有气体实验定律为II级要求,即要求考生能够理解并运用气体实验定律解决相关实际问题。在2019年高考中,全国三套试卷中的选考第33题第2小问,完全遵循考试大纲的要求,分别从不同角度考查了学生对气体实验定律的运用。全国卷I以实际生产、生活中用于材料加工的热等静压设备为背景,要求学生根据题意建立恰当的气体变化模型,运用气体实验定律解决相应问题。全国卷II则以连通的气缸活塞为模型背景,学生在平时的考试或者练习中也见过此类模型,因此并不陌生。通过对活塞的受力分析和对气体的变化过程分析,可以解决相关问题。全国卷III以玻璃管模型对学生的能力以及学科素养进行考查,这一模型学生也比较熟悉,通过分析玻璃管中封闭气体倒置前后的压强变化,利用玻意耳定律可以解决细管的长度问题,加热封闭气体,气体压强不变,利用盖-吕萨克定律可以求出密封气体的最终温度。
1 原题呈现
(2019年全国卷III) 如图1,一粗细均匀的细管开口向上竖直放置,管内有一段高度为2.0 cm的水银柱,水银柱下密封了一定量的理想气体,水银柱上表面到管口的距离为2.0 cm。若将细管倒置,水银柱下表面恰好位于管口处,且无水银滴落,管内气体温度与环境温度相同,已知大气压强为76 cmHg,环境温度为296 K。
(i)求细管的长度;
(ii)若在倒置前,缓慢加热管内被封闭的气体,直到水银柱的上表面恰好与管口平齐为止,求此时密封气体的温度。
(i)该问难度不大,根据题意可知,理想气体的变化过程为等温过程,需要用到玻意耳定律PV=C。假设细管的横截面积为S,长度为L,水银柱高度为h,水银柱上表面到管口的距离为h',初始时,气体的压强为P1,体积为V1,末状态(倒置时)气体压强为P2,体积为V2。
2 遇到的问题及解决策略
教学中可以发现,关于这类考题主要涉及的模型有气缸与活塞模型、玻璃管与U型管模型两类,解决这些问题通常需要列出三个方面的方程:力学方程,即上下表面气体的压力差大小等于重力或者其他力的合力;热学方程,即利用气体实验定律列出气体对应的规律方程;关系方程,即气体压强与外界大气压以及液体高度之间关系的方程[1-3]。常见的U型管问题包括液面下降高度问题、加入水银问题、气体长度变化问题以及这些问题的综合。笔者在教学中发现,学生对于U型管问题处理时经常出现状态分析不清、气体变化过程分析不清、压面高度差寻找、初末状态参量寻找、所列方程关系混乱、求解出错等问题。为此,笔者鼓励学生通过“一寻、二画、三列式”的“三步曲”分析这类问题,可以较为有效地形成解题思路并解决问题。
“一寻”,指寻找关键词。寻找题中的关键词信息,即判断出气体的变化过程是等压、等容,还是等温过程,进而判断所需采用的气体实验定律。
“二画”,指画等高线。利用连通器原理,液面等高处压强一样,所以一般需画出初末状态液面对应的等高线,能够更快地判断出液面高度之间、压强之间的关系。
“三列式”,指列出相应表达式。列出表达式,一般而言需要根据气体实验定律和液面的几何长度关系列出对应的气体参量方程和气体体积关系方程,而后求解相关参量。
笔者利用高三复习课中的三个常见例题进行说明。
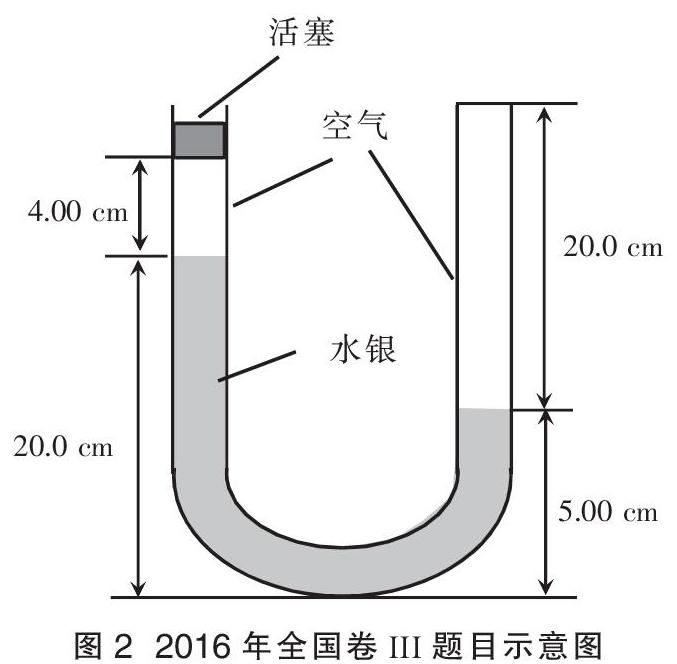
例1 (2016年全国卷III)一U型玻璃管竖直放置,左端开口,右端封闭,左端上部有一光滑的轻活塞。初始时,管内汞柱以及空气柱长度如图2所示。用力向下缓慢推动活塞,直至管内两边汞柱高度相等时为止。求此时右侧管内气体的压强和活塞向下移动的距离。已知玻璃管的横截面积处处相同,在活塞向下移动的过程中,没有发生气体泄漏,大气压强P0=75.0 cmHg。环境温度不变。
分析 此题为气体压缩求活塞移动距离问题,需要同时考虑气体压缩以及液面下降距离。
“一寻”,题中“环境温度不变”,即其中涉及气体的变化过程均为等温过程,即PV = C(玻意耳定律),因此需要确定初末状态的P和V。
“二画”,画初末状态等高线(等压线),如图3所示,可以明顯看出左侧液面下降x,右侧液面上升x,最终液面平齐,由此得到2x=20-5,也可分析出右侧气柱长度由20 cm变成了20-x=12.5 cm。初始状态左侧气体压强为P0,根据等高线,可以得到右侧气柱初始压强P1=75 cmHg+15 cmHg=90 cmHg,初始体积V1=S·20 cm3。末状态体积为V2=S·(20-7.5) cm3。
最终,左右两侧液面高度一致,左侧气体压强为P3=P2=144 cmHg,初始状态压强为P0=75 cmHg,初始体积为V0=S·4 cm3,由于初末状态的PV=C,因此最终左侧气体的长度L3为:
例2 (模拟题)如图4所示,在粗细均匀的U型管右侧,用水银封闭一段长L1=19 cm、温度T1=280 K的气体,稳定时,左右两管水银面高度差为h=6 cm。已知大气压强为P0=76 cmHg。
(1)给右管密闭气体缓慢加热,当右管内气体温度为多少时,两管水银面等高。
(2)若不给右管密闭气体加热,而是向左管缓慢补充水银,也可使两管水银等高,求补充水银柱的长度。
对于第1小问而言:
“一寻”,寻找题目中的关键词,发现气体的温度、体积、压强均在变化,故需要采用理想气体状态方程PV/T求解相关参量。
“二画”,画出初末状态的等高线(如图5所示),可以明显看出右侧液面下降x1,左侧液面上升x1,最终液面平齐,由此得到2x1=h,于是x1=3 cm。
“三列式”,采用理想气体状态方程求解参量,需要求出初末状态的三个参量。初始状态:
对于第2小问,可以发现对应的封闭气体为等温过程,左侧加入水银后,压强发生变化,右侧液面也会发生变化。假设右侧液面上升高度为x2,通过画出的等高线(如图6所示),可以明显地看出左侧液面上升h+x2,列出的表达式为:
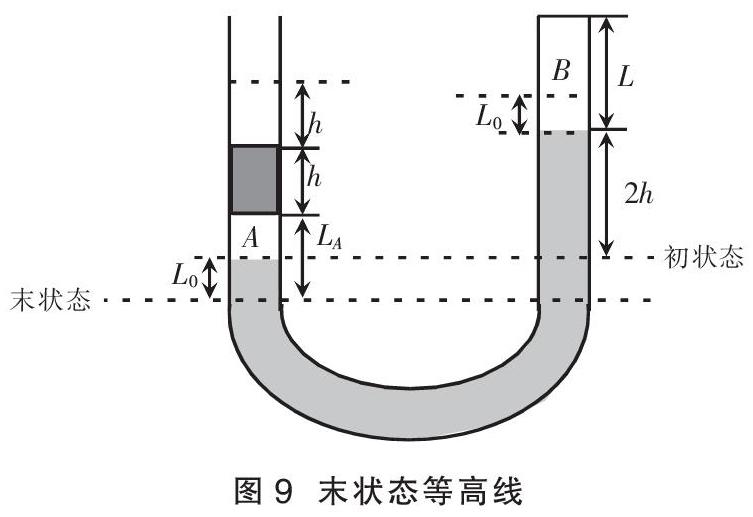
例3 (模拟题)如图7所示,粗细均匀的U型玻璃管,竖直放置,左端开口,右端封闭。右端封闭了一定质量的理想气体B,气柱长为L=12.5 cm,左端长为h=4 cm的水银柱封闭了一定质量的理想气体A,气柱长度也为h,且两端最上方液面齐平。现再往左端缓慢加入长为h的水银柱。已知大气压强为P0=76 cmHg,整个过程温度保持不变。当气柱稳定时,求:右端液面上升的高度L0及气柱A的长度LA(计算结果均保留一位小数)。
分析 该题液柱中包含气体,需要求解液面上升高度以及气柱长度问题。
“一寻”,通过题目可以发现,A和B气体均属于等温过程,即PV = C(玻意耳定律),故需确定初末状态的P和V。
“二画”,画等高线需从U型管底端计算,由于气体压强处处一致,与液体不同,因此等高线(等压线)以下不可有气体,如图8所示。
以上是笔者针对热学中的U型管模型常见的液面高度、加入液柱长度、气柱长度问题中,鼓励学生采用的快速解决问题的思路与方法。不足之处,请读者不吝赐教。
参考文献:
[1]曹少平. 分类讨论在热学解题中的应用[J]. 物理教师, 2019,40(4):65-68.
[2]沈锐. 热学计算题求解思路及题型汇总[J]. 中学物理教学参考, 2016,45(10):84-85.
[3]靳建设,淮萍萍,陈勇. 2019年高考物理备考专题——热学部分[J]. 中学物理教学参考,2019,48(1-2):112-124.
(栏目编辑 陈 洁)
