探析水银外溢问题的通解

■湖南省株洲市第二中学 朱兴中

题目：如图1所示,长度为Lcm,粗细均匀的玻璃管开口向上,竖直放置,管内用长度为hcm的水银柱封闭一定质量的理想气体,气体的初始长度为L0cm,温度为T0K。设大气压强为p0cmHg,若使水银柱全部溢出,则应对气体加热到多高的温度？

图1

分析：在水银柱的上端面到达管口之前,气体发生的是等压变化,根据盖-吕萨克定律(C为常数)可知,随着气体体积的增大,其温度也一定升高。从水银柱上端面到达管口位置开始考虑,当水银柱的溢出长度为xcm 时,因其温度,即T∝pV,故接下来只需要考虑pV的变化即可。因为pV=(p0cmHg+hcmHg-xcmHg)(Lcmhcm+xcm),其中0≤x≤h,所以pV-x图像为开口向下的抛物线,零点x1=h-L＜0,x2=p0+h＞h,对称轴,它的三种可能性如图2甲、乙、丙所示。

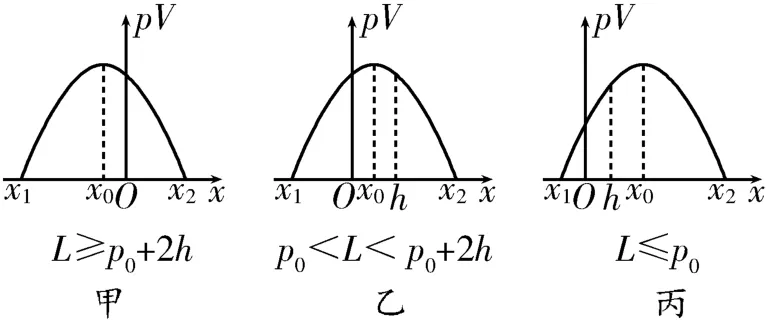
图2

在图2 甲中,x0≤0,即L≥p0+2h,在0≤x≤h的范围内图像递减,故从x=0状态气体开始降温,水银自动溢出,须加热到的最高温度;在图2 乙中,0＜x0＜h,即p0＜L＜p0+2h,在0≤x≤h的范围内图像先递增再递减,故从x=x0状态气体开始降温,水银自动溢出,须加热到的最高温度;在图2 丙中,x0≥h,即L≤p0,在0≤x≤h的范围内图像递增,故须一直加热到水银柱的下端面到达管口位置为止,此时的温度。

例1如图3所示,将长度为L,粗细均匀的玻璃管开口向上,竖直放置,管内用长度h=5 cm 的水银柱封闭一定质量的理想气体,气体的初始长度L0=50 cm,温度T0=300 K。设大气压强p0=75 cmHg,试求下列三种情景下使水银全部溢出所需加热到的最高温度Tmax。

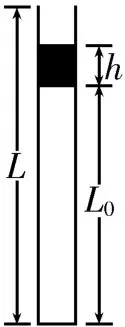
图3

①L=90 cm;②L=80 cm;③L=70 cm。

解析：①当L=90 cm 时,对应L＞p0+2h的情景,此时x0=-2.5 cm＜0,即只需加热到水银柱的上端面到达管口即可,此后气体降温,水银自动溢出,故须加热到的最高温度。

②当L=80 cm 时,对应p0＜L＜p0+2h的情景,此时x0=2.5 cm,即水银柱溢出2.5 cm 时达到最高温度,此后气体降温,水银自动溢出,故须加热到的最高温度Tmax=。

③当L=70 cm 时,对应L＜p0的情景,此时x0=7.5 cm＞5 cm,即需要一直加热到水银柱的下端面到达管口为止,故须加热到的最高温度。

例2如图4所示,粗细均匀的U 型玻璃管竖直放置(底端水平),左端封闭,右端用一段水银柱封闭一定质量的理想气体,温度T0=300 K。玻璃管左右两端高度相同,图中L0=20 cm,L1=30 cm,L2=10 cm,h=10 cm。若大气压强p0=75 cmHg,现在均匀加热管内封闭气体,试求使水银全部溢出所需加热到的最高温度Tmax。

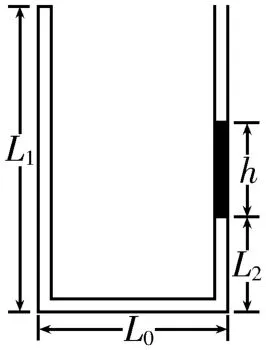
图4

解析：设溢出水银柱长度为x时,玻璃管内封闭气体的温度为T,玻璃管的横截面积为S,根据理想气体状态方程得数学表达式代入数据解得因此当x=7.5 cm 时,Tmax=450.3 K,此后水银自动溢出,气体温度开始降低。

例3如图5所示,长度为L,粗细均匀的玻璃管开口向下,竖直放置,管内用长度为h的水银柱封闭一段长为L0、温度为T0的空气柱。设大气压强为p0,均匀加热管内封闭气体,试求使水银柱全部溢出所需加热到的最高温度Tmax。

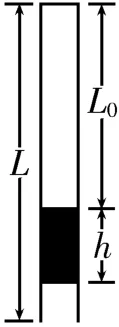
图5

解析：设溢出水银柱长度为x时,玻璃管内封闭气体的温度为T,玻璃管的横截面积为S,根据理想气体状态方程得 数 学 表 达 式解得T=,表明随着x(x＞0)的增加,T也增大。因此当x=h时,气体的温度最高,且。

小结:求解水银外溢问题的基本思路是从最根本的理想气体状态方程入手,准确描述各种情景下压强p和体积V的特征,通过合乎物理条件的数学分析,求得正确答案。

拓展：若将玻璃管内长度为h的水银(密度为ρ)换成另一种密度为ρ'的液体,则描述其产生压强对应的高度应换算成,但描述其对体积影响的长度仍为h;若玻璃管与水平面成夹角θ放置,则描述水银柱产生压强对应的高度应换算成h'=hsinθ,但描述其对体积影响的长度仍为h。