叶片角度对输水泵站泵装置水力性能影响分析

施伟，成立

(1. 南水北调东线江苏水源有限责任公司，江苏 南京 210019； 2. 江苏省泵站工程技术研究中心，江苏 南京 210019； 3. 扬州大学水利科学与工程学院，江苏 扬州 225000)

立式轴流泵装置是低扬程泵站常用的一种泵装置形式，其进、出水的形式由泵站规模、布置要求、附属设施形式以及投资经济性等因素确定.目前，大型泵站的进水建筑物的形式较多地采用肘形进水流道、斜式进水流道，与开敞式的进水池相比，一方面节省了土建开挖量，另一方面能够为水泵提供更好的入流流态.出水建筑物虹吸式出水流道、低驼峰式出水流道和直管式出水流道均较为常用[1-2].中型泵站的进水建筑物常用的形式有开敞式进水池、封闭式进水池、肘形进水流道.对于运行台时较长的调水、供水泵站，考虑到运行的经济性和安全稳定性，一般选用水力性能较好的肘形进水流道和直管式出水型式[3-4].

随着水泵叶片调节技术的发展，内置式叶片全调节机构的安全可靠性进一步提高，中型立式轴流泵站已具备叶片全调节机构的技术条件[5-7].因此，为提高效益，中型泵站在供水工程等长时间运行的应用场合，更多地采用全调节技术.随着叶片角度调节的变化，泵装置的水力性能也会受到影响.谢丽华等[8]针对15°斜式轴流泵进行水动力特性研究发现，泵装置在小叶片角度下的空化特性优于大叶片角度；陈红勋等[9]采用数值计算和试验相结合的方法对轴流泵液压式叶片调节结构调节过程受力进行研究，结果表明叶片调节力均随着叶片角度增加而逐渐减小；程炀等[10]针对不同叶片角度下轴流泵装置特性进行数值模拟，研究表明不同叶片角度下进水流道压力脉动差异较大.目前，传统的水泵选型方式还是以满足设计工况的要求为主，通过设计工况下的水力性能优劣来选择设计运行角度，忽视了对满足设计工况运行条件的水泵装置在其他叶片角度运行的水力性能分析.

文中以某大型供水工程低扬程立式轴流泵站为研究背景，基于CFD技术和模型试验，对设计流量工况不同叶片角度下泵站泵装置进水流道、出水流道流动及叶轮内流特性和水力性能进行研究，以期为实际工程提供参考.

1 计算模型及方法

1.1 计算模型

泵站单机设计流量为8 m3/s，设计扬程为5.5m，以研究泵站单台机组为计算模型，包括进水延伸段、肘形进水流道、叶轮、导叶、直管式出水流道、出水延伸段.根据泵站原型尺寸建立三维数值模型，如图1所示.水泵叶轮直径D=1500 mm，叶片数为4，导叶片数为7，转速为250 r/min.

图1 泵站单机组计算模型

1.2 湍流模型

泵装置内部流动近似认为是不可压缩流体的湍流流动，可采用三维雷诺时均N-S方程(RANS)计算分析其流动特性和水力性能.湍流模型采用RNGk-ε模型，这是一种RANS方法常用的涡黏模型，采用重整化群统计方法，通过修正湍动黏度和增加时均应变率项来考虑流动中的旋流情况，适用于各种泵装置流动特性的稳态模拟，特别是带有肘形进水流道的泵装置水力性能模拟[11-13].

1.3 计算网格及边界条件

文中研究的计算模型组成部件较多，较为复杂.整体划分网格难以控制质量，并且叶轮和导叶的结构相对复杂，其内部水流流动变化急剧，需要相对精细的网格捕捉流动特性，因此采用分块网格剖分策略.应用Turbogrid软件对叶轮、导叶用结构网格进行剖分，肘形进水流道、直管式出水流道及进、出水延伸段等采用Mesh软件中非结构网格剖分.叶轮、导叶网格如图2a所示.为减少网格对计算结果的影响，对整个计算域进行网格敏感性分析，对整体计算域网格进行调控，设置了6个不同网格数N的方案，并进行数值模拟，且对比各方案的扬程计算结果.计算结果表明网格单元数达到千万量级时，泵装置的扬程波动值小于1%.为了保证精度和计算效率，取网格数为1 200万.网格敏感性分析如图2b所示.

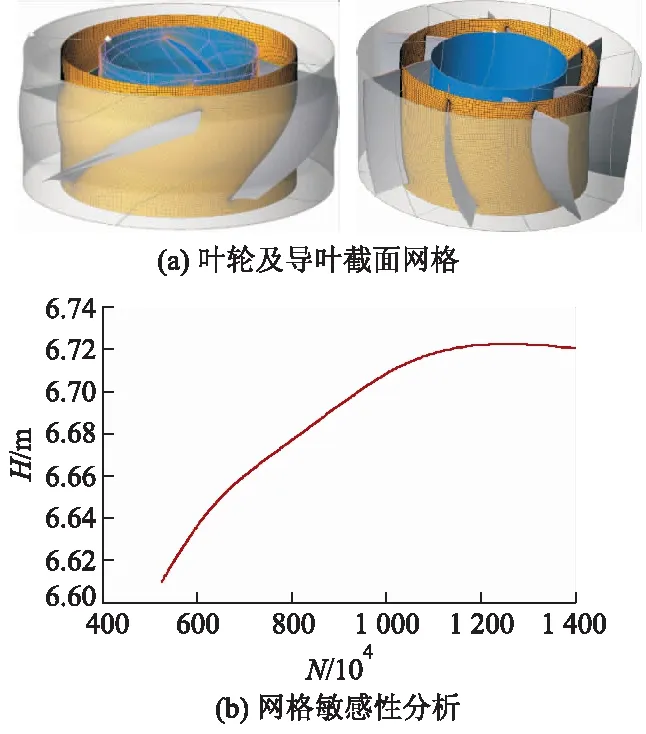
图2 计算网格示意及网格敏感性分析

计算进口设置在进水延伸段进口，进口边界条件为流量进口；计算出口设置在出水延伸段出口，出口边界条件为压力出口，进水延伸段表面为自由对称水面，采用刚盖假定设置为symmetry.对固体壁面采用无滑移边界条件，在近壁区采用壁面函数.对于泵站而言，包含旋转的叶轮，静止的导叶和进、出水流道，其中进水流道与叶轮、叶轮与导叶之间有相互流动耦合作用，设置为动静交界面.计算格式为高阶迎风，收敛精度为10-4.本次计算流量范围为7.0～10.5 m3/s，叶片角度为-8°,-6°,-2°,0°,+2°.

1.4 性能预测模型

由计算得到流速场和压力场，根据伯努利能量方程计算泵装置净扬程，通过数值积分计算叶轮上作用的扭矩，从而预测泵装置的效率.

将泵装置进水流道进口1-1与出水流道出口2-2的总能量差定义为泵站扬程，即

(1)

式中：H1,H2分别为断面1-1和断面2-2的高程，m；p1,p2分别为断面1-1和断面2-2的压力，Pa;u为速度，m/s；S1,S2分别为断面1-1和断面2-2的面积，m2；Q为流量，m3/s；ρ为水的密度；g为重力加速度，m/s2.式(1)右边的第1项为断面2-2和断面1-1的静压能水头差，第2项为断面2-2和断面1-1的高程差，第3项为断面2-2和断面1-1的动能水头差.

因此，水泵装置的效率为

(2)

式中：Tp为扭矩，N·m；ω为叶轮角速度，rad/s.

2 数值模拟计算及分析

2.1 泵装置能量性能曲线

文中研究的供水泵站是某个供水系统的1个环节，其运行的性能既要满足系统特性，还要具有较高的效率，因此需要根据运行的实际情况调整叶片的运行角度α.图3为-8°～+2°角度下原型泵装置经数值计算得到的能量性能曲线，由图可知，当流量为8m3/s，叶片角度α由-2°到+2°时，扬程为6.10～7.10m，满足设计工况要求，效率为76.6%～80.8%.根据《泵站设计规范》对轴流泵站装置效率不低于70.0%，南水北调工程建设专用技术规定平均扬程5m的泵站效率达到73.0%的要求，该装置在叶片角度-2°～+2°时能量性能较好.

当流量为8m3/s，叶片角度为-6°时，扬程为4.36m，效率为75.4%；叶片角度为-8°时，扬程为3.49 m，效率为69.3%.在流量为8m3/s，叶片角度从+2°变为-2°，效率下降了4.2%；叶片角度从-2°变为-6°，效率下降了5.6%；叶片角度从-6°变为-8°，效率下降了6.1%；在叶片角度从- 6°变为-8°的过程中，泵装置的能量性能下降较从-2°变为+2°时急剧.

图3 不同叶片角度下泵装置的能量性能

Fig.3 Energy performance of pumping system at different blade angles

2.2 不同叶片角度下进、出水流道内流态

图4为叶片角度α为-8°,-6°,-2°,0°,+2°，流量为8m3/s时，肘形进水流道速度v分布情况.由计算可知，各个角度下，肘形进水流道内水流沿着流道几何轮廓转向平滑，无回流区，流道内流速变化均匀，进水流态较好.

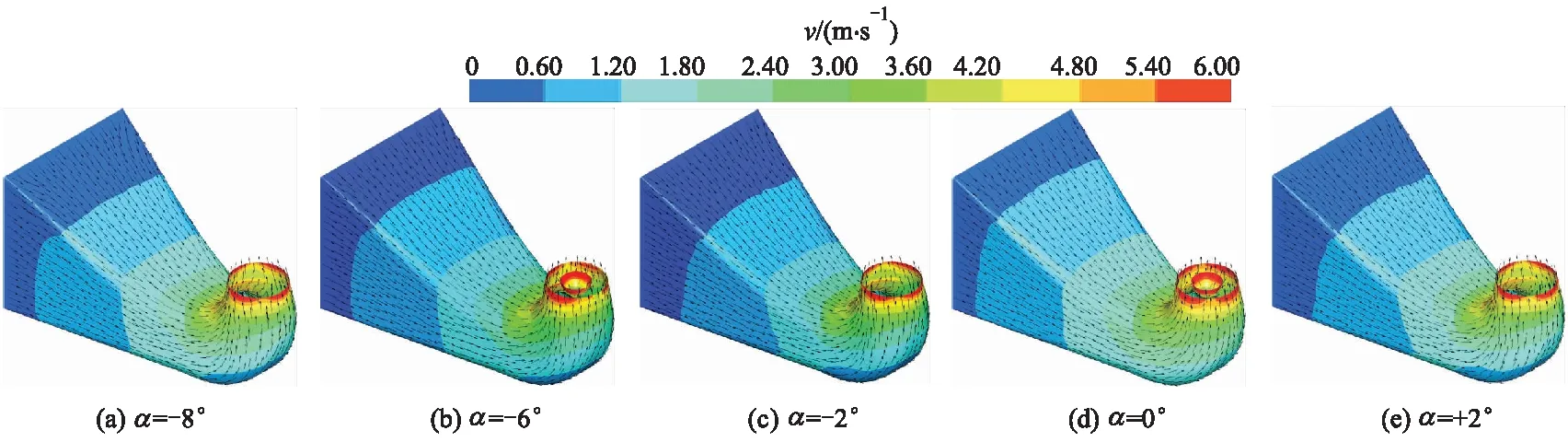
图4 不同叶片角度下进水流道的流态

(3)

(4)

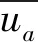
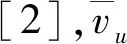
表1 肘形进水流道出口流态和水力损失

Tab.1 Flow pattern at outlet and hydraulic loss of elbow inlet passage

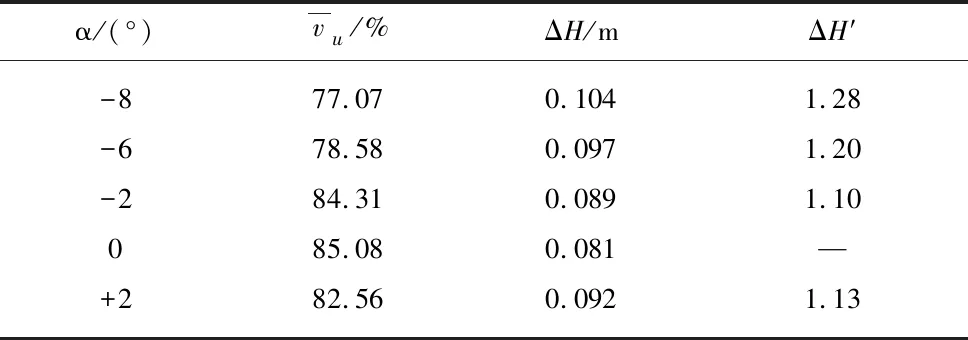
α/(°)vu/%ΔH/mΔH′-877.070.1041.28-678.580.0971.20-284.310.0891.10085.080.081—+282.560.0921.13

图5为叶片角度为-8°,-6°,-2°,0°,+2°时，出水流道流速分布情况.由图可知，叶片角度为0°，流量为8m3/s时，出水流道水流流速分布较为均匀；叶片角度为-8°，-6°，-2°，+2°时，直管式出水流道沿水流方向进口侧存在明显的且范围较大的局部低压区和高压区.由此表明，叶片设计运行角度发生变化，偏离设计运行角度，进入出水流道的水流流态较差，存在局部的回流区.

图5 不同叶片角度下出水流道的流态

表2为直管式出水流道入流涡角和水力损失.入流涡角是评价出水流道入口水流流态的一项指标，定义为轴面平均切向速度与轴向平均速度的比值.入流涡角越大，水流流入出水流道的环量越大，流态越差.由表2可知，流量为8m3/s时，叶片角度为0°的出水流道入流涡角θin最小，水力损失也最小.叶片角度偏离0°越大，入流涡角越大，水力损失也增大.研究表明，在流量不变情况下，叶片角度偏离设计角度，出水流道入流流态变差，水力损失增大.

由表1，2可知，为保证一定的流量，在水位发生变化，进行偏角调节时，进水流道的水力损失变化相对较小，水力损失相对值最大为1.28(叶片角度-8°)；出水流道水力损失变化相对较大，水力损失相对值最大为2.89(叶片角度-8°)，叶片角度变化对出水流道流态影响较大.

表2 直管式出水流道入流涡角和水力损失

Tab.2 Inflow vortex angle and hydraulic loss of straight pipe outlet passage

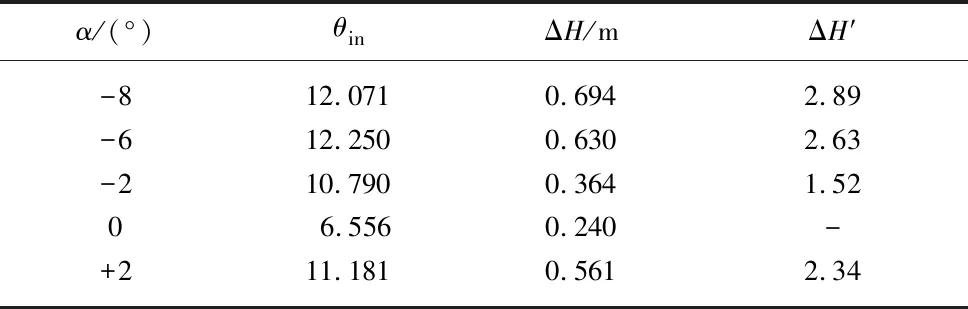
α/(°)θinΔH/mΔH′-812.0710.6942.89-612.2500.6302.63-210.7900.3641.5206.5560.240-+211.1810.5612.34

2.3 不同叶片角度下叶轮内流态

S为叶轮内部某一点到轮毂的距离与轮缘到轮毂的距离比值，当S=0.1时，所取剖面上的所有点都满足其到轮毂的距离与对应位置轮缘到轮毂的距离之比为0.1.图6为S=0.1，流量为8m3/s时，叶片角度为-8°,-6°,-2°,0°,+2°的轴向速度vz分布翼展图.

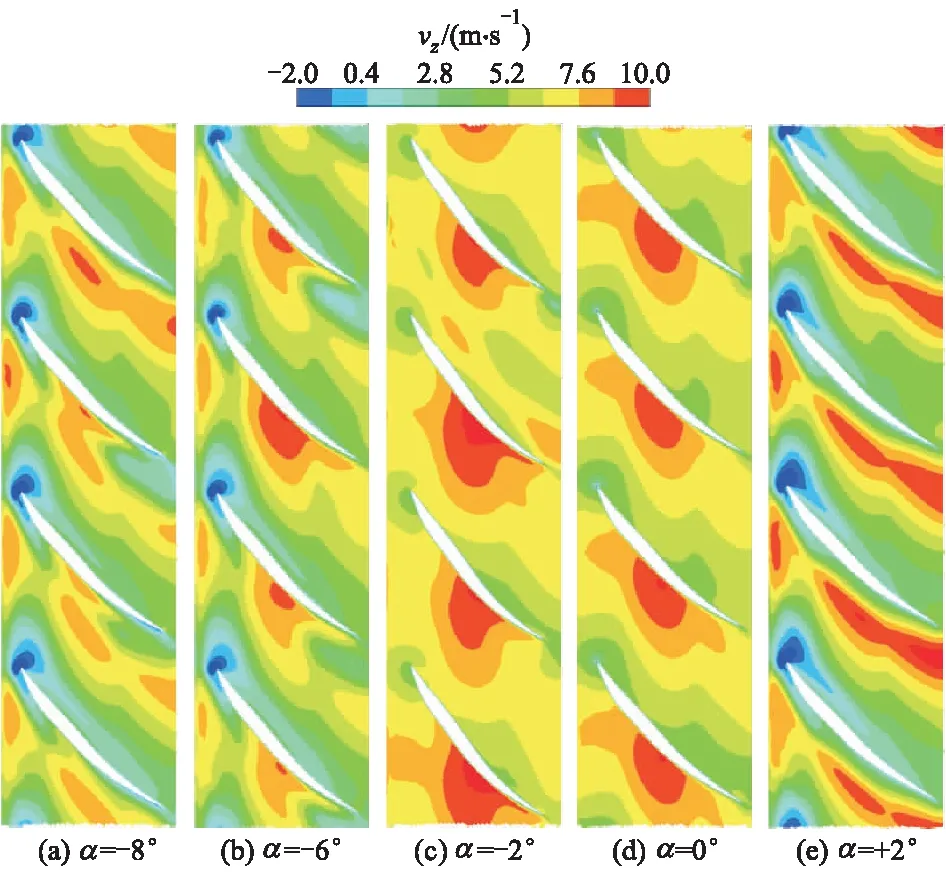
图6 叶轮轴向速度分布翼展图

由图6可知，叶片角度为-8°,-6°,+2°时，靠近轮毂的区域，叶片头部存在小范围的回流区.这是由于叶片角度变化，叶轮在偏设计工况运行，叶轮内出现脱流、回流的现象.这种脱流、回流发生在叶轮的进口靠近轮毂的区域，也影响了进水流道的水流流动，使得进水流道的出口流态变差，水力损失增大.

3 模型试验

为进一步验证数值计算的可靠性，进行了模型试验研究.水泵装置模型比例为1∶5，模型叶轮直径D=300 mm，叶片数为4，用黄铜材料加工成型.模型导叶叶片数为7，用钢质材料焊接成型.进出水流道采用钢板焊接制作，模型泵装置如图7所示.模型泵安装检查，导叶体与叶轮室定位面轴向跳动0.10 mm，轮毂外表面径向跳动0.08 mm，叶顶间隙控制在0.20 mm以内.

图7 泵装置模型

图8为叶片角度为0°时，CFD预测能量性能与试验结果对比.由图可知，流量为8m3/s时，CFD预测扬程为6.724m，预测效率为80.2%，试验测得扬程为6.801m，效率为78.5%.扬程的相对偏差为1.1%，效率相对偏差为2.1%，均在5.0%以内，表明在流量为8m3/s时，CFD预测结果与试验结果吻合较好.

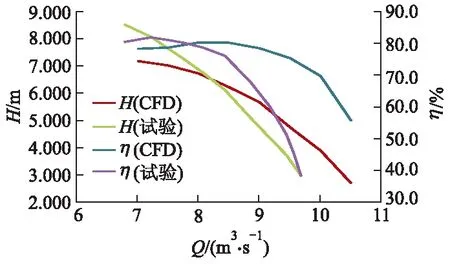
图8 CFD和试验结果对比

4 结 论

1) 叶轮叶片角度调节对叶轮及出水流道影响较大，在非设计角度下，叶轮进口近轮毂区存在回流、脱流.叶片角度偏离设计工况角度越大，进水流道出口速度均匀度越差，出水流道进口环量也越大，导致进水流道、出水流道内水流流态越差；同等偏离角度下，出水流道水力损失增大幅度较进水流道显著.

2) 采用模型试验对数值模拟结果进行了验证，在设计流量工况下，叶片角度为0°时，扬程相对误差为1.2%，效率相对误差为2.1%，两者吻合较好.

3) 对于运行工况变化较大、运行时间较长的输水泵站，采用变角调节时，应在设计中，对不同叶片角度下泵装置的流动特性进行分析及优化.