蜗壳式混流泵轴向力的数值计算与试验验证

董志强

(上海凯士比泵有限公司，上海 200245)

轴向力作为泵的重要设计参数之一，与泵自身的安全性、稳定性、经济性密切相关.工程实践中，过小的预测轴向力将导致机组振动、噪音、温升等指标超标，甚至发生泵轴断裂、机组损坏等重大事故，影响泵自身性能和使用寿命.汪燕[1]利用经验对照法、类比法、系统安全评价法对某泵站断轴事故进行了详细分析，发现轴向力是断轴产生的首要因素；反之，过大的评估轴向力会引发泵自身体积和重量增加，造成不必要的浪费，降低设计的合理性及经济性.因此，准确计算泵的轴向力意义重大，也是泵的重要研究课题之一[2-7].

泵轴向力的常用计算方法有理论计算法、试验法、数值计算法.理论计算法建立在盖板腔体无泄漏的假定之上，对经验系数的依赖程度较高且不同理论公式的计算结果差异较大.刘在伦等[8]提出基于平衡腔液体压力数学模型的轴向力计算方法，并将轴向力计算结果与测试实例试验结果进行对比，验证了方法的可靠性，设计工况下相对误差约25%.高红俐等[9]以分段式多级离心泵为例，采用多种不同计算公式分别对其轴向力进行计算，通过与试验结果进行对比，评估了不同公式计算结果的差异性，相对误差为-270%～800%.试验法须借助一套专用测试系统来测量泵的轴向力，不仅成本高昂，而且往往需要在泵盖处或推力轴承处额外设计相应的接口以布置测点，增加了结构设计的复杂性.数值计算法经济性高、时间成本低，且不受泵自身结构、使用工况的限制，学者们对此进行了大量研究[4, 10-13].然而，针对盖板腔内压力引起的轴向力，现有研究中仍需借助泵腔压分布理论或试验测量，完全依靠数值模拟、考虑盖板腔内泄漏流动的轴向力计算的相关研究较少.

文中以某工厂生产的立式、单级、单吸、蜗壳式混流泵为研究对象，采用CFD数值方法分别对基于泵腔压力分布理论的无泄漏模型和基于泵腔流动的泄漏模型进行轴向力计算，并将数值计算结果与理论计算结果、轴向力试验结果进行对比，详细分析了不同轴向力计算方法的准确性及泄漏流动对轴向力计算的影响.文中的研究结果可为混流泵轴向力计算提供一定的参考.

1 模型构建

研究所用混流泵的叶轮为闭式叶轮，其额定点参数如下：转速nopt=1 450 r/min，流量Qopt=1 128.3 m3/h，扬程Hopt=15.46 m.叶轮的具体参数如下：叶轮进口直径D1=300.0 mm，叶轮出口中径D2=260.0 mm，泄压孔分布圆直径Drh=115.0 mm，泄压孔数量Z=4，泄压孔直径drh=16.0 mm，叶轮前密封环直径Drs2=316.0 mm，叶轮前密封环间隙宽度Srs2=0.2 mm，叶轮前密封环间隙长度Lrs2=9.0 mm，叶轮后密封环直径Drs1=234.5 mm，叶轮后密封环间隙宽度Srs1=0.2 mm，叶轮后密封环间隙长度Lrs1=9.0 mm.

1.1 基于压力分布理论的无泄漏模型构建

泵腔压力分布理论假定盖板腔体内泄漏量为0，腔内液体只作单一的环形旋转，无径向流动，并以1/2的叶轮旋转角速度旋转[14].如图1所示，采用NX 11.0软件对混流泵全部流体域，包括进水流道、叶轮、蜗壳、盖板前腔、盖板后腔进行建模，其中，盖板前腔进行建模、盖板后腔均只在叶轮出口处通过密封环间隙与蜗壳流域连通，腔体本身无其他接口或泄漏口.

图1 无泄漏模型结构图

1.2 基于泵腔流动的泄漏模型构建

泵腔内液体的真实流动情况如图2a所示，叶轮出口高压区部分液体通过密封环间隙流入盖板前腔、盖板后腔，盖板前腔内液体通过叶轮与泵体的间隙a泄漏至叶轮进口；盖板后腔内一部分液体通过泄压孔b泄漏至叶轮进口，另一部分液体通过轴封c泄漏至泵体外.采用NX 11.0软件对混流泵全部流体域进行三维建模，如图2b所示.

图2 泄漏模型结构图

2 数值计算

采用ANSYS 18.0软件的ICEM模块对混流泵整个流场域的各个部分进行六面体结构化网格划分，其中叶轮壁面处y+控制在1～60，如图3所示.以泵出口压力及盖板前、后腔内压力作为监测量，进行网格无关性验证.网格总数最终选定为930万，最低网格质量控制在0.45以上.

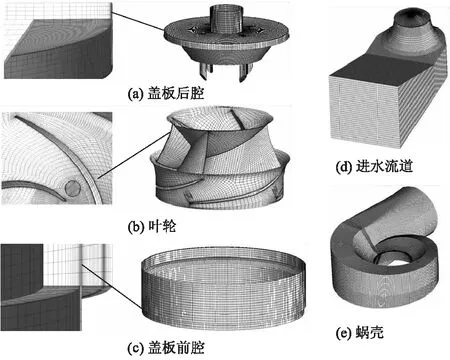
图3 网格示意图

考虑到叶轮旋转域内部流场比较复杂且流线弯曲程度较大，文中数值计算选用RNGk-ε湍流模型，与多重坐标下的连续性方程及N-S方程构成封闭计算方程组；基于SIMPLEC算法，求解压力与速度的耦合；采用2阶中心差分格式进行扩散项的离散，1阶迎风格式进行对流项的离散，收敛精度设置为10-4.为了提高小流量工况下的计算准确性及收敛鲁棒性，动静交界面采用Stage边界条件，同时将大流量下收敛的计算结果作为小流量工况的计算初值.

3 数值计算结果及分析

3.1 外特性性能分析

图4为混流泵外特性曲线对比图，图中Q/Qopt为流量比，H为扬程，η为效率.从图中可以看出，在0.80Qopt～1.20Qopt流量下，计算结果与试验结果较为接近，其中无泄漏模型预测扬程、效率的最大误差分别为3.2%，3.4%，泄漏模型预测扬程、效率的最大误差分别为3.6%，1.1%；在0.03Qopt～0.50Qopt流量下，2个模型的数值计算结果均小于试验结果，计算偏差随着流量的减小而增大，其中扬程的预测偏差较小，无泄漏模型、泄漏模型扬程的最大误差分别为4.7%，5.1%；效率预测偏差较大，无泄漏模型、泄漏模型效率的最大误差分别为42.8%，48.7%.这主要是由于小流量工况下泵内流态极为复杂，从而导致数值计算精度下降，出现了效率计算失真的现象.对比2个模型的预测曲线，泄漏模型预测的H-Q，η-Q曲线均低于无泄漏模型预测曲线，且η-Q曲线下降的幅度大于H-Q曲线的.这是因为泄漏流动产生的容积损失对机组效率的影响较大，对机组扬程的影响较小.

文中基于无泄漏模型与泄漏模型对混流泵外特性的数值计算数据与试验数据变化趋势完全一致.除小流量工况下效率计算值偏差较大外，预测曲线与试验曲线吻合度较高(最大误差均在5.0%以内)，特别是泄漏模型对额定工况下机组效率的预测具有较高的精度，验证了文中数值计算方法的可靠性及准确性.

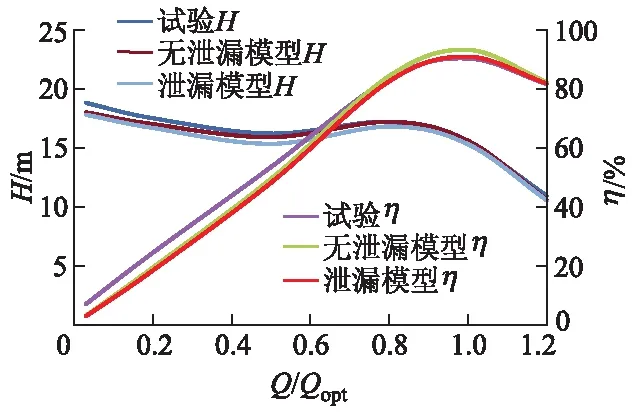
图4 外特性曲线

3.2 分项轴向力计算

如图5所示，按照IEC 60193标准[15]绘制水动力F1(方向向上)、上盖板力F2(方向向下)、下盖板力F3(方向向上)曲线，其中转子部件重力F4、叶轮浮力F5、静压力F6与泵内流动无关，因此未绘制曲线.无泄漏模型与泄漏模型计算的F1随流量变化的曲线形状相近，但同一流量下其数值存在差异，特别是在0.03Qopt～0.50Qopt小流量工况下，无泄漏模型计算值明显大于泄漏模型的计算值.这是因为盖板腔内的泄漏流对叶轮区域内主液流会产生一定的影响，导致叶轮内部压力场发生变化.对于上盖板力F2及下盖板力F3，无泄漏模型的计算曲线均大幅高于泄漏模型的计算曲线，同时2个模型计算的F2差值和F3差值均表现为随流量的减小而增大.这说明盖板腔内泄漏流动对其内部流态具有显著的影响，能够有效降低腔内压力，且这种影响随着流量的减小而增大.F1，F3方向与混流泵轴向力方向相反，能够起到平衡轴向力的作用；与F1，F3相比，F2方向与混流泵总的轴向力方向相同且数值较大，约为F1与F3之和的2倍.由此可见，盖板后腔内部压力是混流泵轴向力产生的主要因素.

图5 分项轴向力对比曲线

3.3 后腔压力分布及流态分析

根据文献[16]的研究结果，结合文中分项轴向力计算结果，可以看出泵体后腔内部压力是轴向力产生的主要原因，也直接决定了轴向力大小.因此，文中以盖板后腔为研究对象，对其内部压力分布规律及流态进行分析.

为了消除压力在圆周方向分布不均的影响，如图6所示，提取叶轮盖板上相同半径下0°，45°，90°，135°，180°，225°，270°和315°的压力均值，并绘制压力均值沿径向的分布曲线.盖板后腔内部压力随着半径的增大呈上升趋势，压力曲线整体近似于一条上升的弧线，局部类似于抛物线，但随着半径的减小，曲线变得更加平缓，如图7，8所示，图中p为压力均值，r为半径.不同工况下盖板腔内压力分布规律存在差异，采用泵腔压力分布理论无法对其进行准确描述.

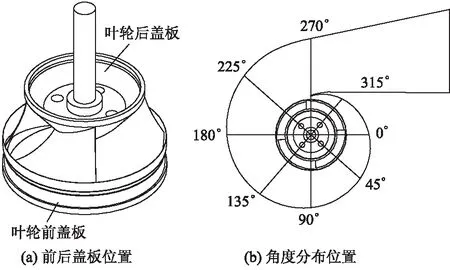
图6 压力提取位置示意图

对比图7，8可以清晰地看出：同一流量工况下，与无泄漏模型相比，泄漏模型盖板后腔内部压力整体偏低，仅为无泄漏模型的60%～75%，压力曲线分布更陡峭、梯度更大；不同流量工况下，无泄漏模型计算的盖板后腔压力曲线近似相互平行，相同半径处的压力、扬程随流量变化规律一致；泄漏模型计算的盖板后腔压力曲线在0.03Qopt～0.80Qopt流量下出现局部相交，特别是0.80Qopt流量下，r在80.0～234.5 mm时的压力曲线高于其余工况下的压力曲线.

图7 无泄漏模型盖板后腔压力分布曲线

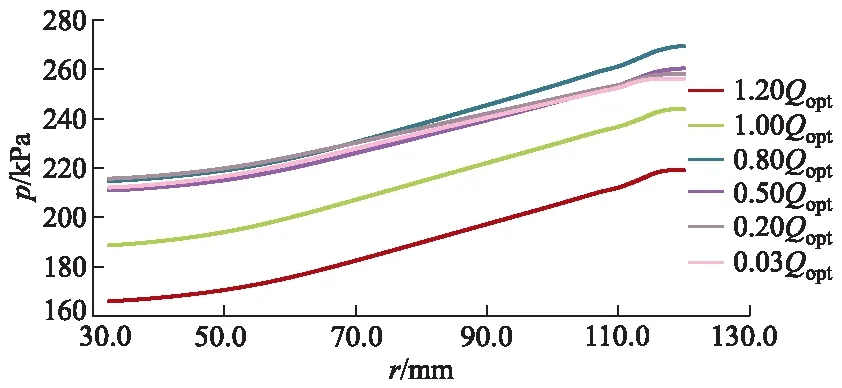
图8 泄漏模型盖板后腔压力分布曲线

出现上述现象的可能原因如下：无泄漏模型盖板后腔封闭，液体由密封环间隙流入并充满腔体后，腔内液体与叶轮区域液体之间不流动；相同转速下，密封环间隙及盖板后腔液体流态受运行工况的影响较小，产生的阻力损失近似相等，压力的大小主要取决于叶轮出口压力.而泄漏模型盖板后腔进口通过密封环间隙与叶轮出口区域连通，通过泄压孔与叶轮进口区域连通，通过轴封与外部大气连通，2个泄漏口相对于进口均属于低压区，进而形成泄漏流，并与叶轮区域主液流彼此影响，此时盖板后腔压力受到叶轮出口压力和液体流经密封环间隙产生的阻力损失的共同影响；相比0.80Qopt工况，0.03Qopt工况下叶轮内部流动更复杂，作为入流边界，直接导致密封环间隙内部流态更紊乱，流经密封环间隙产生的阻力损失更大，使0.03Qopt工况下盖板后腔进口处压力值低于0.80Qopt工况对应的压力值.

为了评估泄漏流动对盖板后腔内部流态的影响，以Qopt工况点为例，提取盖板后腔内部45°，135°，225°，315°圆周方向所对应的轴向平面流线图，如图9，10所示，其中v为流线速度.

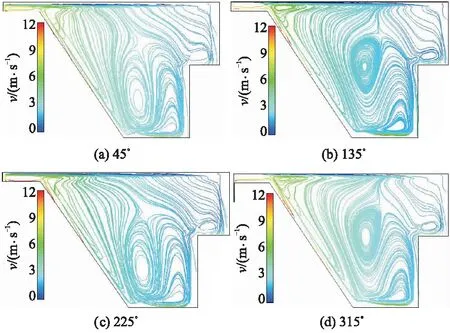
图9 无泄漏模型盖板后腔流线分布图

Fig.9 Streamlines distribution map of non-leakage model

从图9，10中可以看出，泄漏模型中，盖板后腔内液体流态十分紊乱：腔内液体在叶轮旋转作用下，在圆周方向上绕轴旋转；径向上则受腔体形状、泄压孔回流、轴端泄漏等因素的影响，形成较多“涡带”，最终流入叶轮进口及泵体外.径向流速随着半径的减小而减小，变化范围在3～12 m/s ；不同圆周角度下的流态存在明显差异，这是因为受到叶轮旋转、蜗壳形状、隔舌位置等因素影响，叶轮区域内出现了非对称流，进而导致盖板后腔内液体流动在圆周方向存在一定的不均一性，进一步验证了盖板腔内泄漏流与叶轮区域主液流之间存在相互影响.无泄漏模型中，径向流速仅在进口局部区域存在小范围变化，腔内大面积区域的径向流速均在3 m/s左右；不同圆周角度下的轴面流态存在局部差异，但整体趋势一致，均表现为沿腔体内壁近似做等速旋转运动.

图10 泄漏模型盖板后腔流线分布图

4 试验验证及结果分析

4.1 轴向力试验

轴向力试验在某国家重点水力试验室进行.试验原理如下：驱动电动机通过柔性联轴器与泵轴相连；该联轴器的主要作用是将电动机扭矩传递给泵轴，其自身不能承担任何轴向力；混流泵转子部件的重量及工作中产生的轴向力均由测量试验台上的静压式推力轴承承担.当泵处于静止状态时，作用在静压式推力轴承上的轴向力仅由转动部件的重量产生，此时轴承前、后腔体压差为Δp0；当泵运转时，叶轮处产生的轴向力通过刚性轴传递到推力盘，进而使推力轴承前、后腔体压差上升至Δp1.此时，叶轮产生的轴向力F计算公式为F=(Δp1-Δp0)·SAM，其中SAM为推力轴承腔体的有效面积.混流泵总的轴向力为叶轮产生的轴向力与自身转动部件的重力之和.试验原理简图如图11所示.

图11 轴向力测量装置结构图

4.2 轴向力理论计算

根据文献[11]推荐的混流泵轴向力计算公式，并结合研究所用混流泵相关参数进行轴向力理论计算.盖板腔内压力p的计算公式为

(1)

式中：p2为叶轮出口静压力，Pa；ω为叶轮旋转角速度，ω=2πn/60，rad/s；r2为叶轮出口半径，m；ρ为介质密度，kg/m3.对式(1)从轮毂直径积分到密封环直径，即可计算出作用于盖板的轴向力.

4.3 结果对比与分析

从图12可以明显看出，分别采用理论计算和数值模拟预测的轴向力F随流量变化曲线与试验曲线分布规律一致：随着流量的减小，混流泵轴向力呈上升趋势；在0.50Qopt附近，曲线上出现一段“驼峰”区间.

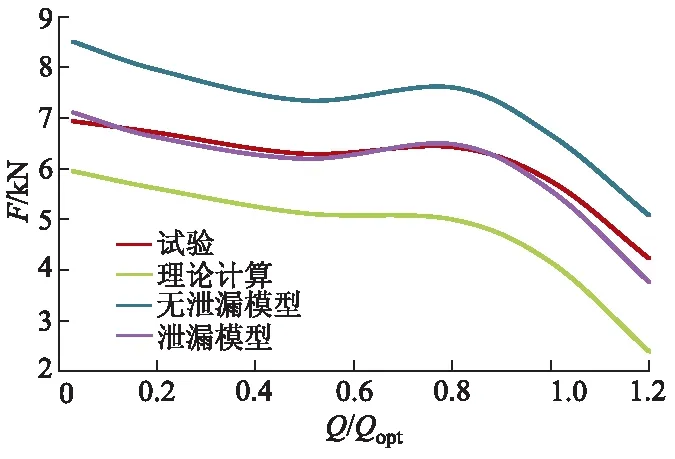
图12 轴向力分布曲线

不同工况下，理论计算的机组轴向力均小于试验数据，误差范围在18%～44%；无泄漏模型数值模拟的不同流量下轴向力均大于试验数据，误差范围在14%～25%，且计算误差随流量的减小而增大；泄漏模型数值模拟的轴向力与试验数据较为接近，除了1.20Qopt工况计算误差10%略高外，其余工况的轴向力计算误差均在3%左右，计算精度有了较大幅度的提升，特别是在临近关死点的0.03Qopt工况下，基于泄漏模型的轴向力数值计算精度比无泄漏模型提升了23%，比理论计算法提升了15%.这说明文中提出的基于泵腔流动的泄漏模型数值计算方法可较准确地预测混流泵的轴向力，能为混流泵的工程设计提供科学指导.

5 结 论

1) 基于泄漏模型的混流泵轴向力数值计算方法预测结果与试验结果十分接近，最大误差小于10%，计算精度比轴向力理论计算法、基于无泄漏模型的混流泵轴向力数值计算法均有较大幅度的提升，说明该方法具有更高的准确性和可行性.

2) 叶轮盖板后腔内部压力是混流泵轴向力产生的主要因素，泄漏流动可以较大幅度地降低腔内液体压力，理论计算法和基于无泄漏模型的数值计算法均忽略了泄漏流动对盖板腔内压力的影响，导致轴向力计算结果存在较大误差.

3) 同一流量下，盖板腔内液体压力随半径的增加而增大，压力曲线类似于一条上升弧线；与无泄漏模型相比，泄漏模型预测的盖板腔内液体压力更小且随半径的变化率更大，压力曲线更陡峭.

4) 盖板腔内的泄漏流动导致其内部液体径向流速表现出随半径减小而减小的变化规律，加剧了内部流态的复杂性；同时，受到叶轮区域主液流的影响，腔内流态在圆周方向上存在一定的不均一性.间隙流与主液流之间的相互影响是后续重点研究方向之一.