翼型间隙空化数值模拟的湍流模型比较分析

陆于衡，冉红娟*，史天蛟，刘永，钱信如

(1． 上海交通大学核科学与工程学院，上海 200240； 2. 中国核动力研究设计院，四川 成都 610213)

间隙泄漏空化现象常见于旋转水力机械，其叶片两侧的压差会使转轮与泵壳的间隙中产生空化.这类流动的湍流特性很强，将导致水力机械产生振动、噪声，从而影响效率.许多学者对间隙空化及相关流动进行了试验研究.早期RAINS[1]对压缩机间隙流动进行了研究.覃大清等[2]比较了轴流式水轮机中间隙空化和翼型片状、云状空化的差异.BOULON等[3]通过试验对翼型叶片顶部空化进行了研究，分析了不同间隙尺寸及壁面对空化的影响.张德胜等[4]通过流场可视化研究，发现轴流泵叶顶区域是空化最严重的区域.HIGASHI等[5]、DREYER等[6]利用流场可视化方法对间隙泄漏流动进行了研究，获得了流动及流场几何参数对间隙泄漏空化形态的影响.

由于空化试验对流速和设备要求较高，因此数值模拟成为重要的研究方法.WATANABE等[7]根据二维间隙空化的研究，对间隙涡空化的模型进行了修正.赵宇[8]、郭嫱[9]均根据间隙泄漏空化的特性，对空化模型进行了优化.CHENG等[10]利用SST-CC湍流模型和涡识别空化模型对翼型的间隙空化进行计算，并讨论了空化对间隙泄露涡产生的影响.

目前，对于翼型间隙泄漏空化的机理已有一些数值模拟研究，但针对不同湍流模型对计算影响的分析还比较少.文中对比3种不同湍流模型模拟间隙空化流动时的结果，并利用修正密度的RNGk-ε湍流模型对一定间隙的空化流动进行非定常数值计算，并分析翼型几何特征对间隙泄漏空化特性的影响.

1 数学模型

1.1 控制方程及湍流模型

对于采用了均相流假设的两相流动，涡黏模型的N-S方程可表示为

(1)

(2)

式中：ρm和μm分别为混合相的密度和动力黏度；μt为涡黏模型假设引出的湍流黏度.

目前广泛应用于计算的k-ε方程和k-ω方程中，其湍流黏度的表达式分别为

(3)

(4)

GIRIMAJI等[11]由k-ε模型发展了PANS模型，近几年来，该湍流模型得到了较好的发展. PANS模型中定义了未求解湍动能、耗散率与总湍动能、耗散率的比值fk和fε，并对耗散率输运方程中的耗散系数进行了修正，使fk和fε可以对湍动能与耗散率的输运方程产生影响.PANS模型中fk和fε分别定义为

(5)

(6)

其湍动能与耗散率的输运方程分别为

(7)

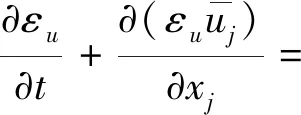
(8)

式中：

(9)

(10)

其中，σk，σε，Cε1和Cε2均为标准k-ε模型中的系数.

考虑到空化流动的可压缩性，COUTIER-DELGOSHA等[12-13]通过在涡黏模型的湍流黏度表达式中增加1个关于密度的函数，对RNGk-ε模型进行了修正，获得了修正密度(density correction method)的RNGk-ε模型(以下简称“DCM RNGk-ε模型”).该模型中，湍流黏度μDCM和密度修正函数f(n)分别如式(11)，(12)所示，即

μDCM=μtf(n)，

(11)

(12)

式中：ρv和ρl分别为气相和液相的密度；αl为液相体积分数.

1.2 空化模型

文中计算采用Zwart空化模型.它是一种由R-P方程推导发展而来，并得到广泛使用的空化模型.最终得到的蒸发率、凝结率公式分别为

(13)

(14)

式中：Rb为空泡半径，Rb=1μm；rnuc为水中气核密度，rnuc=5.0×10-4；Fvap为蒸发系数，Fvap=50；Fcond为凝结系数，Fcond=0.01.

2 数值计算

为了分析不同湍流模型在模拟间隙泄漏涡空化时的预测能力，文中对不同间隙攻角的翼型流动进行计算，选取DCM RNGk-ε，PANS和SSTk-ω这3种湍流模型进行对比.翼型NACA0009，弦长100 mm，在翼型接近间隙一侧的边缘，有半径1 mm的圆角.流道截面接近正方形，长度150 mm,并设置3°，5°，7°，10°共4个攻角，2，10，15 mm共3个间隙.图1为计算模型示意图.为方便后续分析，在流场区域中建立坐标系，其中坐标原点位于翼型旋转线与壁面的交点.

图1 计算模型示意图

计算区域的网格均采用六面体结构化网格，并进行了无关性验证.验证选取翼型前后缘上方的压力差Δp为监测参数.监测点示意图和无关性验证结果如图2所示，监测点距间隙侧壁面20 mm.由图2b可见，当网格数N达到450万后，监测值已较为稳定.考虑到计算的准确度和计算资源，选取600万的网格进行计算.近壁面网格如图3所示.k-ε，k-ω型湍流模型的表面y+分别为30～80和1～10.

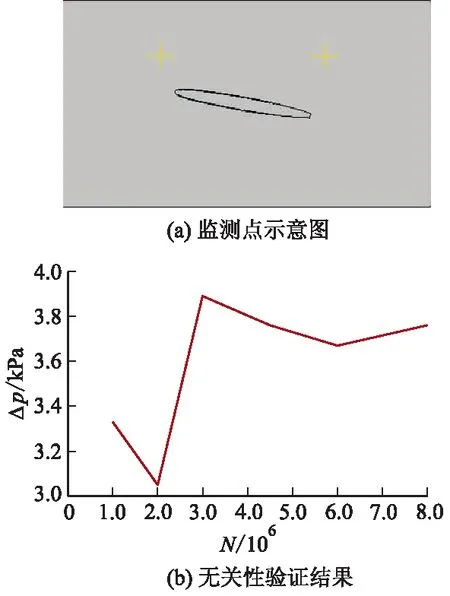
图2 网格无关性验证

图3 计算网格示意图

水的物性取25 ℃，饱和压力取3 174 Pa.进口采用10 m/s的速度条件，出口压力设为100 kPa，选用光滑无滑移壁面，参考压力为0，设置收敛精度为10-5.根据文献[14-15]，PANS模型中湍动能比例取0.6，DCM-RNG模型中n取10，选用Zwart空化模型进行计算，并根据文献[9]将空化模型中凝结系数修正为0.001，以提高其空化预测能力.

3 计算结果分析

3.1 不同间隙条件下气相体积分数分析

将上述计算结果与文献[6]中的试验结果进行对比.图4, 5分别为攻角α=10°，间隙d=2，10 mm时，流场中气相体积分数φ>0.1的区域图.

图4 间隙为2 mm时，不同湍流模型计算的空化形态与试验结果对比

图5 间隙为10 mm时，不同湍流模型计算的空化形态与试验结果对比

由不同间隙空化形态的对比图可知，间隙为2 mm时，3种模型均能对间隙空化的形态进行一定的预测，其中DCM RNGk-ε模型计算得到的空化带长度与试验结果最为接近.但空化涡带直径过大，由PANS模型和SSTk-ω模型计算得到的结果中空化涡带的长度明显短于试验结果.3种模型均能准确预测空化的起始点及空化与翼型的角度和空化涡带向下游发展的趋势，但仍有一定偏差.DCM RNGk-ε模型计算得到的泄漏涡的气相体积分数较PANS有较明显的提高，说明利用密度函数对湍流黏度进行修正能在一定程度上提高模型的空化预测能力.由结果可见，当间隙较大时，空化带与翼型表面较为接近，此时翼型空化可沿主流方向发展得更远.

3.2 不同攻角、间隙主流方向速度对比

翼型压力面和吸力面之间的压差会导致间隙间形成剪切流动，这些流动在达到翼型上面时会形成涡旋流动，局部低压引发了间隙内的附着空化和随主流发展的空化.为分析不同的翼型攻角和翼型间隙对间隙空化的影响，文中结合不同的翼型攻角和间隙尺寸，将距翼型中心1个弦长的涡中心处的主流方向速度与文献[6]中的数据进行对比，截面位置如图6所示.

图6 涡中心速度观测截面示意图

涡中心取观测截面处平面流线因涡旋流动所形成圆环的中心，如图7所示.在不同攻角、间隙尺寸条件下，计算距翼型中心1个弦长的间隙泄漏涡中心主流方向速度，并与文献[6]中的试验结果进行对比，如图8所示，其中vm为主流方向速度.

图7 涡旋中心示意图

计算结果中泄漏涡中心速度随间隙尺寸变化的趋势与试验结果基本吻合，在间隙约10 mm处可取得最大值.在速度预测上，各模型的误差整体比较稳定，主要分布在0.5～1.0 m/s，其中DCM RNGk-ε模型的整体预测结果更准确.

图9，10分别为间隙为10,2 mm时，用不同湍流模型计算所得间隙周围轴向速度云图和文献[6]中试验测得的主流方向速度vm云图的对比图,其中y=0处为翼型转动中心所在位置.从图9可见，间隙为10 mm时，模型能较准确地得到涡的形态和中心轴向速度.间隙较大时，泄漏涡位置较低，与翼型后缘脱落的尾迹存在相互影响.此外，从图9，10中可见涡中心与流道壁面间存在较大的速度梯度.间隙为2 mm时，计算对泄漏涡的形态预测有所偏差，对涡中心的速度预测过高，且压力梯度较小，如图10所示.小间隙条件下，泄漏涡距翼型上表面更远，且不易受到翼型后缘尾迹的影响，但泄漏涡距间隙壁面更近，壁面条件会对涡产生更大影响.在上述间隙条件下，产生的泄漏涡中心速度较主流速度更低，不易产生空化，因而小间隙时，翼型上方的空化区域较短，空化更早溃灭.结合试验和计算图，发现在翼型后方，泄漏涡的中心位置偏离间隙，说明间隙间的剪切流动在到达翼型吸力面后存在向翼型吸力面侧的流动，并促进了间隙泄漏涡的形成.

图8 主流方向速度随间隙尺寸变化示意图

图9 间隙为10 mm时，截面处主流方向速度云图

图10 间隙为2 mm时，截面处主流方向速度云图

3.3 间隙空化非定常特性分析

综合考虑3种湍流模型的预测能力及其所需计算资源，选择DCM RNG湍流模型对间隙为10 mm、翼型攻角为10°的流动区域进行非定常计算.入口和出口条件分别选用流速和静压，采用光滑壁面条件；时间步长设置为0.000 5 s,以无空化模型结果作为初始条件.

图11为气相体积分数φ>0.1的流场区域等值面图，图中t0为选取的空化初生时刻.从图中可见，该类空化具有较强的非定常特性.在翼型前缘上方存在附着于翼型表面的片状空化.不同的间隙尺寸对泄漏引起的空化形态影响很大.小间隙条件下，更为强烈的剪切流动将导致泄漏涡空化距翼型上表面更远，间隙空化更为强烈，发生位置更接近翼型前缘.间隙为10 mm时，泄漏空化向下游发展较远，表明在该间隙尺寸条件下，翼型上方由泄漏流动和主流交混所引起的涡旋流动较为稳定.

图11 间隙为10 mm时，间隙泄漏空化随时间发展图

图12为z轴方向上距原点0.4倍弦长处间隙的局部矢量图，其中v为流体速度.从图中可见，泄漏流动在与主流交混后形成了流速较快的涡旋流动，造成该处压力下降较为明显，从而引发空化.翼型压力面处的圆角附近也有较快的速度，而在无圆角的翼型间隙内侧，流动速度的差异更明显.这表明圆角可以减小间隙附近区域流动的突变，引导压力面的流体经间隙向翼型上方流动，使空化发生位置向翼型的吸力面偏移.

图12 距原点0.4倍翼型弦长处间隙局部矢量图

Fig.12 Local vector contour near gap at 0.4 times airfoil chord length from origin

4 结 论

文中利用近年几种应用较广泛的湍流模型，结合经过修正的空化模型，对不同尺寸间隙的翼型绕流流动进行了数值计算，并将计算结果与文献中高速摄像的试验图像和数据进行了对比.研究结果表明：

1) 采用经密度修正的RNGk-ε模型计算间隙泄漏空化流场的结果更为准确.该模型计算所得的流场速度数值与文献结果吻合度更高.密度修正提高了模型对空化的预测能力，计算得到的空化区域更接近实际情形.

2) 不同间隙大小会对间隙泄漏空化的位置、维持时间造成明显的影响.小间隙条件下，间隙内附着空化的发生位置更靠近翼型前缘，泄漏涡引起的空化偏离翼型更远，且溃灭更早.

3) 间隙泄漏空化的发生与泄漏流动以及主流交汇产生的涡旋流动密切相关，涡旋产生的局部低压促进了空化的初生和发展.翼型压力面的圆角可以减小局部流动的突变，促进泄漏流动的发生.