质量不平衡对单叶片叶轮径向受力的影响

张华，陈斌，汪源，徐云峰，王震

(1. 合肥工业大学机械工程学院，安徽 合肥 230009； 2. 蓝深集团股份有限公司，江苏 南京 211500； 3. 南京信息工程大学环境科学与工程学院，江苏 南京 210044; 4.南京合工智能环保研究院有限公司，江苏 南京 211500)

单叶片叶轮由于叶片的非轴对称分布，不仅造成生产过程中动平衡配重困难，更导致实际运行中径向力过大，甚至开机失败.因此，国内外大量学者对单叶片泵的内部流动机理进行了研究，期望能够改善单叶片泵的径向受力情况.

NISHI等[1-2]采用LDV试验和数值模拟研究了单叶片叶轮内的流场分布；SOUZA等[3-4]采用恒定速度法对单叶片叶轮的蜗壳设计进行优化，同时在试验和数值仿真的基础上对单叶片叶轮进行了优化设计.AGOSTINELLI等[5]研究了离心泵径向力分布，给出了多种形式蜗壳泵的径向力随比转数的变化规律.王家斌等[6]介绍了一种单叶片螺旋离心叶轮的测绘及静平衡方法.张华等[7]采用虚拟样机仿真技术对单叶片螺旋叶轮进行了配重，该方法不仅缩短了配重周期，减小配重成本，更提高了叶轮表面光洁度.BENRA等[8]对单叶片泵进行流场模拟，并采用流固耦合计算获得了转子所受的水力激励及振动位移.袁丹青[9]、裴吉等[10]针对单叶片泵，实现了瞬态流固耦合求解与试验的验证，获得了各个转速及流量下单叶片泵转子系统周期性水力激振位移轨迹，为单叶片叶轮的径向力分析提供了参考依据.

从国内外学者的研究成果发现，目前有效减小和改善单叶片叶轮径向力的方法鲜见，因此，文中在前人研究的基础上，综合考虑单叶片叶轮在实际运行中受到不平衡水力径向力以及不平衡质量引起的离心力的共同作用，提出精确控制偏心质量和偏心相位角，利用质量不平衡引起的离心力来平衡部分水力径向力，并基于非定常数值计算、虚拟样机仿真及流固耦合等技术，对该方法的可行性进行验证.

1 水力设计

根据标准GB3215—2007和API610—2004规定，对于旋转部件，当零件的最大外径与宽度比值D/b>6.0时，零件的配重可以在1个端面上进行.因此，选择低比转数离心叶轮进行研究，确定设计参数：流量Q=15 m3/h，扬程H=15 m，转速n=1 450 r/min，比转数ns=45.表1为本次单叶片叶轮及蜗壳的水力设计参数结果，其中D1,D2,D3分别为进口直径、出口直径和蜗壳基圆直径；b2为出口宽度，φ为叶片包角；β1,β2分别为进口安放角和出口安放角，b3为蜗壳进口宽度.根据设计结果中D/b值，该叶轮满足单端面配重要求.

表1 单叶片螺旋离心叶轮的水力设计参数

Tab.1 Hydraulic design parameters of single-blade spiral centrifugal impeller

设计参数取值设计参数取值D1/mm60D2/mm220b2/mm25φ/(°)250β1/(°)17β2/(°)15D3/mm230b3/mm45

2 定常数值计算与试验验证

对全流场计算区域进行三维造型，包括叶轮、蜗壳、进水管、出水管及前后泵腔，如图1a所示.对所有计算水体进行六面体结构化网格划分，如图1b所示.以N-S方程为基本控制方程，采用MRF相对旋转坐标系法进行定常数值计算.调用标准k-ε湍流模型，采用scalable壁面函数.进口设置为速度进口，出口设置为压力出口.旋转区域与静止区域采用动静转子交界面.

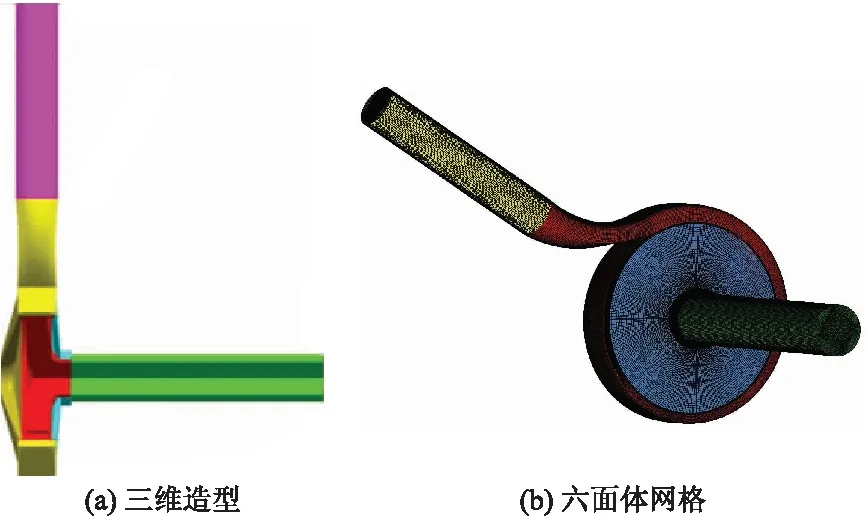
图1 全流场数值计算区域的三维造型及网格划分

Fig.1 3D modeling and hexahedral structured mesh of numerical calculation area of whole flow field

为保证试验模型与设计模型的一致性，对叶轮、蜗壳等主要水力部件采用3D打印的方式进行制造.图2a为试验现场.对6～36 m3/h工况范围内进行定常数值计算，为不考虑质量偏心及其他机械因素的影响，外特性试验仅验证对比扬程-流量曲线，如图2b所示，图中H为扬程，Q为流量.从图中可以看出，在设计工况下，数值计算扬程与试验扬程极为接近.大流量工况下，试验扬程高于数值计算扬程；小流量工况下则相反，符合一般低比转数离心泵的仿真规律.数值计算与试验获得的扬程-流量曲线走势基本一致，因此，定常数值计算结果可信.

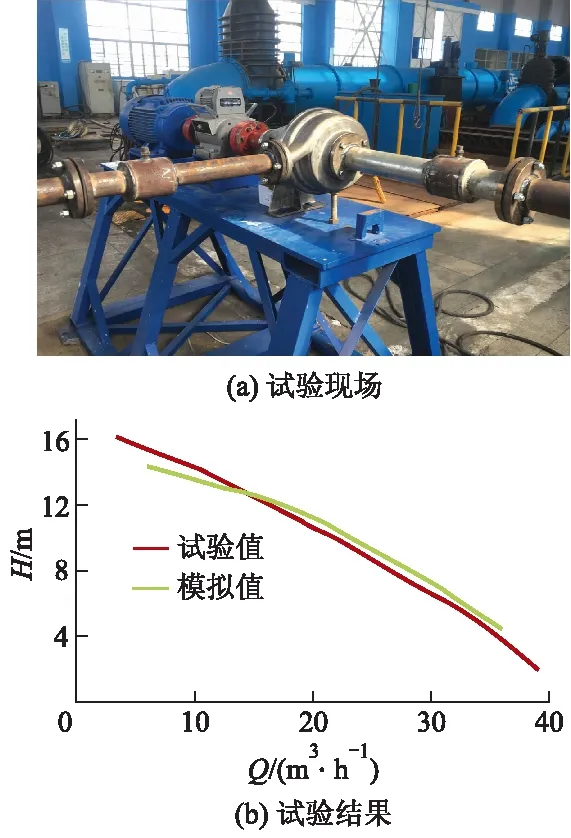
图2 外特性试验

3 非定常数值计算

叶轮所受径向力为瞬时特征，为掌握单叶片叶轮所受径向力情况，应进行非定常数值计算研究.对0.8Qd，1.0Qd和1.2Qd这3个工况进行非定常数值模拟.以定常数值计算结果作为非定常数值计算的初始条件.以叶轮每转动3°作为1个计算步长，即时间步长为0.000 34 s，共计算6个周期，总计720个步长，将最后的稳定周期作为分析对象.

图3为不同工况下叶轮径向受力的矢量分布图(FX为X轴方向受力；FY为Y轴方向受力).从图中发现，3个流量工况下，径向受力曲线呈现椭圆形分布，而且随着流量的增加，径向受力分布曲线不断向外围扩散；扩散的同时，椭圆的中心点越接近坐标原点，并在第二象限内，径向受力分布曲线存在突变.图4为整周期内径向力合力Fr的变化趋势，θ为转动角度.从图中可知，3个工况下，径向力合力的走势基本呈与正弦波相反的趋势，在整周期内，各自出现1次最大值、最小值，并都在25°附近出现突变.

图5为叶轮径向力合力最大、最小与突变时对应的叶轮与蜗壳相对位置.由图可以看出，径向力突变时，叶轮出口边的位置正好旋转至蜗壳隔舌附近.径向力最大时，叶片出口边指向蜗壳第五与第六断面之间；径向力最小时，叶片出口边指向蜗壳第二断面附近.3个工况下，径向力最大、最小与突变时，叶轮与蜗壳的相对位置基本接近.

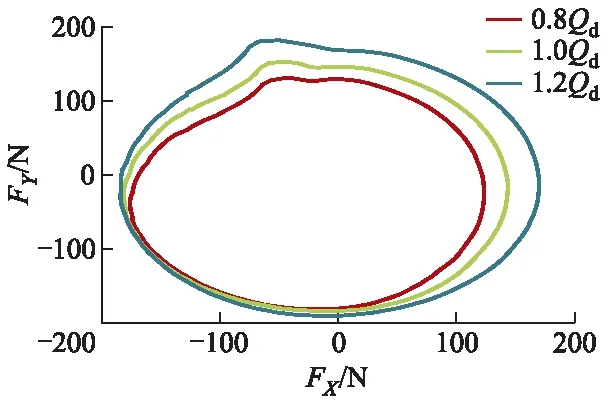
图3 不同工况下的叶轮径向力矢量分布

Fig.3 Radial force vector distribution of impeller under different working conditions

图4 整周期内径向力合力的变化趋势

图5 径向力合力最大、最小与突变时叶轮与蜗壳的相对位置

Fig.5 Relative position of impeller and volute in case of maximum, minimum and sudden change of radial force

4 虚拟样机仿真

从图4可发现，3个工况下，叶轮所受径向力的方向，始终随着叶轮的旋转而旋转，即与叶轮的相对位置固定，仅受力的大小在变化，因此可以考虑通过设计偏心质量的叶轮来平衡部分水力径向力.

以Adams软件为虚拟样机仿真平台，导入叶轮三维模型，设置与实物一致的材料属性，在配重端面与转轴相交位置添加轴承副，设置旋转速度为1 450 r/min，设置叶轮旋转1周经过720个步长.假设叶轮转轴为Z轴，则监测轴承副上Y轴方向的受力大小，根据受力最大时对应的步长，找到需要配重的相位角.根据力的大小及配重半径，计算出配重质量m为

式中：F为偏心力，N；R为配重半径， m；v为配重点的速度， m/s.

以叶轮后盖板的外表面为配重表面，经过多次调整与仿真，最终Y轴方向的受力最大值为0.3 N，几乎接近平衡状态，将此叶轮记为叶轮A.

根据前面的非定常数值计算结果，统计整周期内不同时刻下，叶轮径向受力方向与叶轮出口边之间的夹角，发现叶轮所受径向力的方向与叶轮的相对位置固定，夹角约为78°，如图6所示.

以设计工况为对照，对1个整周期内的径向力大小求平均值，结果约180.0 N，并在水力径向力的反方向进行加重处理.根据上述公式及叶轮尺寸进行初步计算，获得需要配重的重量，采用相同的方法对叶片后盖板外表面进行配重，为保证叶轮后盖板的变形量，采用加重和去重的方式同时进行，最终保持在径向力的反方向上，获得约180.0 N的离心力，该精确配重后的叶轮记为叶轮B.

图6 水力径向力与叶片出口边的相对位置

Fig.6 Relative position of hydraulic radial force and blade outlet edge

最终质量平衡的叶轮及精确配重后的偏心质量叶轮三维图如图7所示.

图7 2只叶轮的三维形状

5 流固耦合仿真分析

研究单叶片叶轮转子系统的真实受力，必须同时考虑转子系统的机械不平衡引起的离心力与水力径向力.由于2只叶轮的盖板形状发生变化，因此必须对2只叶轮重新进行数值计算.设计工况下，重新进行定常全流场数值模拟，发现盖板形状变化后，对扬程几乎没有影响.

对2只叶轮分别建立转子系统的三维模型，并进行网格划分，如图8所示.设置材料属性后，根据实际水泵结构，在轴承位置设置圆柱约束，切向为自由运动，轴向固定.最后设置旋转条件，并监测整个转子系统的等效应力分布及变形量分布，以及转子系统的受力情况.

图8 转子系统的网格

在设计工况下，对叶轮A,B分别进行非定常数值计算，并将2只叶轮的非定常数值计算结果分别作为单向流固耦合时流体载荷的加载边界条件.

对水力径向力在突变位置、最大位置及最小位置3个相对位置进行统计分析，如表2所示，表中l为最大变形，s为最大等效应力.从表中可以看出，3个相对位置下，在未加载流体载荷时，2只叶轮各自的最大变形量及最大等效应力基本相同，说明仿真具有高度可重复性，数据可靠.在未加载流体载荷时，叶轮B的最大变形量及最大等效应力值均大于叶轮A.加载流体载荷后，3个相对位置下，叶轮B的最大变形量均小于叶轮A.

另外，从表2中还可以看出，未加载流体载荷时，突变位置、最大位置及最小位置，叶轮A径向力的大小均为16.6 N，叶轮B径向力大小都在183.8 N附近，叶轮B的径向力明显大于叶轮A.加载流体载荷后，叶轮A不同位置所受的径向力在不断变化，在突变位置时径向力为185.1 N，在最小位置时径向力为195.6 N，在最大位置时径向力为209.1 N.而叶轮B在突变位置时径向力为41.9 N，在最小位置时为37.4 N，在最大位置时为41.6 N.由此可知，对于单叶片转子系统的径向受力，可以通过精确控制质量偏心的方式进行抵消.

表2 单向流固耦合统计结果

6 结 论

采用数值计算、虚拟样机仿真、流固耦合及试验研究相结合的方法，研究了偏心质量对单叶片泵转子系统受力的影响，并获得以下主要结论：

1) 当单叶片叶轮出口边旋转至蜗壳隔舌附近时，会引起径向力的突变，因此，实际应用中可考虑加大蜗壳基圆直径.

2) 采用虚拟样机仿真技术进行单叶片叶轮的动平衡配重，能够获得质量平衡的叶轮，更可以精确控制叶轮的偏心质量及相位角.该方法简单、周期短、成本低，还能够保证叶轮的表面光洁度.

3) 通过精确控制单叶片叶轮的不平衡质量大小及不平衡相位角，利用不平衡质量引起的离心力，能够抵消一部分水力径向力，从而减小实际运行中的转子系统受力，延长轴承寿命.研究可为单叶片泵的发展提供参考和借鉴.