HTPB推进剂蠕变本构方程研究*
2020-05-13罗一智沙宝林
罗一智,沙宝林,侯 晓
(中国航天科技集团有限公司四院四十一所,西安 710025)
符号说明
σ——应力,MPa
εcr——蠕变应变

t——时间,s
S-H——应变硬化方程缩写
T-H——时间硬化方程缩写
M-T-H——改进时间硬化方程缩写
M-S-H——改进应变硬化方程缩写
g1、g2…g4——表示函数关系,无具体形式
G1、G2、G3——表示函数关系,无具体形式
a、b、c、d——为简化方程形式引入的中间量
e、f、r、p——为简化方程形式引入的中间量
A、B、C——为简化方程形式引入的中间量
0 引言
固体火箭发动机经历长期的立式贮存工况,承受温度载荷、自重载荷,药柱产生蠕变变形发生下沉,甚至阻塞排气通道,这些因素都对发动机的结构可靠性和寿命产生影响[1]。对于药柱长期立式贮存的特殊工况及蠕变效应,近些年愈来愈得到重视。国防科技大学的沈怀荣[2],研究了复合固体推进剂的温度相关的蠕变损伤模型;针对大力神-4固体助推器的立式贮存问题[3],国外研究人员利用Rocstar程序包进行模拟,研究大变形情况;南京理工大学的李东等[4-5],针对双基固体推进剂,基于幂律蠕变模型,结合试验数据,研究药柱本构关系和蠕变特性;袁军等[6]针对大型固体发动机,考虑温度载荷和内压载荷的作用,进行燃烧室有限元分析;王永帅等[7]基于时间硬化蠕变方程,研究舰载导弹发动机的蠕变效应;Bihari等[8]采用经典的Kelvin-Voigt模型,对推进剂的粘弹特性进行研究,建立了蠕变粘弹的数学模型;海军航空大学的王鑫等[9-11],对于HTPB推进剂,基于时间硬化模型,研究了考虑蠕变效应的立式贮存发动机在多种载荷作用下的应力应变状态。然而,至今有关固体发动机的蠕变效应研究,多采用时间硬化蠕变方程。前人关于蠕变方程的研究则多集中于金属和岩石领域,对于固体推进剂的蠕变本构方程及其适用性的全面研究尚未见报道。
本文针对某配方HTPB推进剂发动机的立式贮存问题,开展了多应力水平的蠕变试验。根据试验数据,拟合了多种蠕变本构方程,并对其适用性进行了研究。
1 试验
1.1 试验仪器与方案
试验仪器为CMT4203-3A蠕变应力-松弛仪。该仪器的最大试验力为2 kN,准确度等级为0.5级,试验力测量范围为10%~100%,试验力示值分辨力为最大试验力的1/300 000,试验力示值相对误差为示值的±0.5%以内,位移示值相对误差±0.5%,位移分辨为0.03 μm。试验箱使用温度为-30~100 ℃,温度波动度为±2 ℃。
试验对象是某配方HTPB推进剂试件,试件依照QJ 924—1985《复合固体推进剂单向拉伸试验方法》规定执行,推进剂配方如表1所示。

表1 典型HTPB推进剂配方
蠕变试验在常温下进行,考虑到HTPB试件最大抗拉强度在1 MPa左右、药柱贮存过程中的界面最大应力以及试验过程所需大量时间的限制,分别进行0.4、0.5、0.6、0.7 MPa应力水平的蠕变试验,每个应力水平开展3组试验,通过计算机程序实时记录应力和试件的伸长量。根据标距长度计算蠕变应变,对各应力水平的3组试验取平均值,得到试件的蠕变曲线。蠕变试验装置如图1所示。

图1 蠕变试验装置Fig.1 Set-up for creep test
1.2 试验结果
图2为不同应力水平下的应变-时间曲线。试件受到载荷作用时,首先产生瞬时弹性应变;定载荷的持续作用下,试件应变不断增大。初始阶段,应变率随时间的增长而减小;第二阶段也称为稳态阶段,应变率趋于恒定,应变稳定增大;第三阶段,应变率变大,应变快速增大,试件破坏。应力越大,试件破坏时间越短。
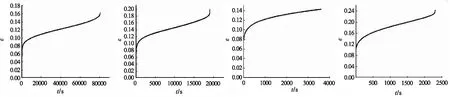
(a)σ=0.4 MPa (b)σ=0.5 MPa (c)σ=0.6 MPa (d)σ=0.7 MPa
2 蠕变本构方程
固体推进剂属于高聚物材料,具有粘弹性特性,在长期自重载荷的作用下,产生蠕变效应。一般情况,蠕变应变率是时间、应力、应变、温度的函数,如式(1):
(1)
对方程进行积分、移项处理,将方程化为
εcr=G1(σ)G2(t)G3(T)
(2)
本文研究的蠕变本构方程[12-13]汇总见表2。
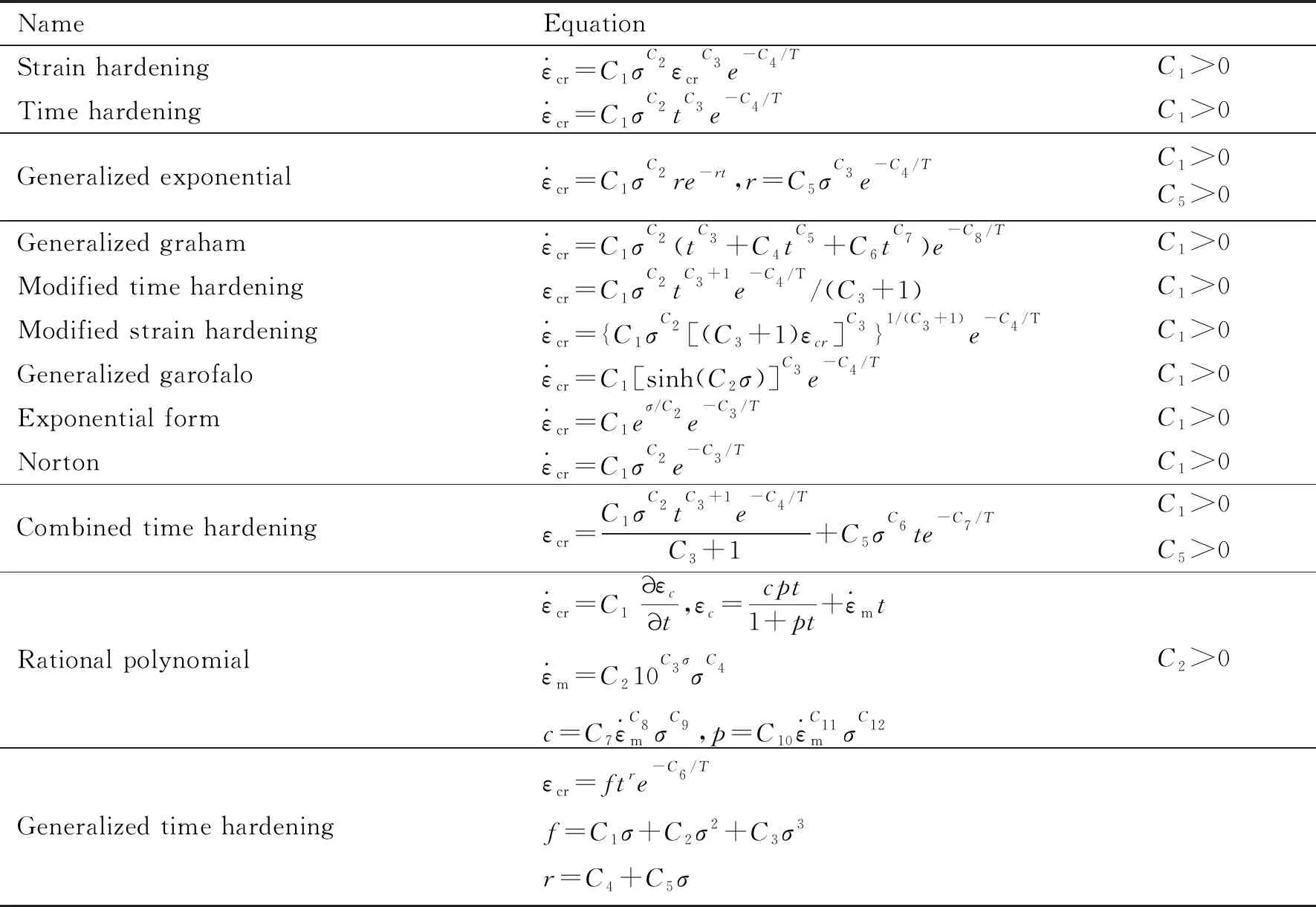
表2 蠕变本构方程
蠕变本构方程包括应力相关项、时间相关项和温度相关项。本文研究对象基于保温筒中发动机燃烧室,温度保持恒定。常温下,不同组蠕变试验的温度保持一致,可忽略方程中的温度相关项,对于温度相关项的系数,进行归零处理;对于某个应力水平下的蠕变试验,应力为定值,G1(σ)为常数,通过G2(t)项描述某定应力水平下的蠕变过程;对于不同应力水平下的蠕变过程,通过G1(σ)项描述规律性。
针对蠕变本构方程研究的总体思路(见图3):
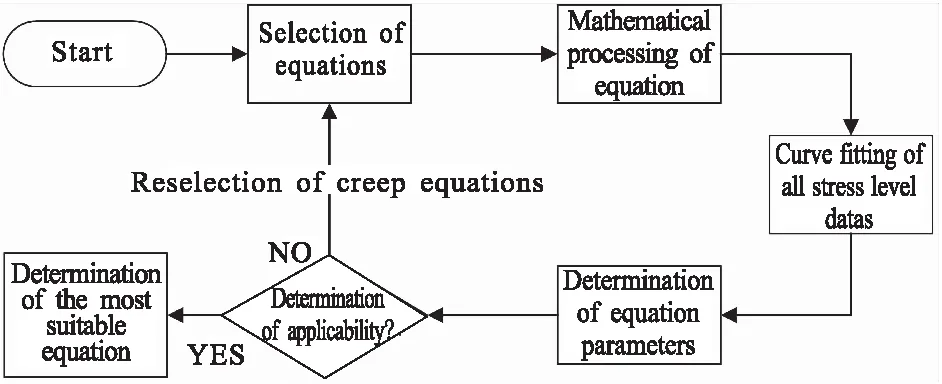
图3 总体研究思路Fig.3 General research process
(1)选择蠕变本构方程,采用最小二乘法针对不同应力的蠕变试验进行数据拟合,确定不同应力水平下的G1(σ)和G2(t)。对于模型参数是非线性的函数,采用Levenberg-Marquardt方法[14]迭代处理。Levenberg-Marquardt方法是非线性最小二乘估计的一种估计方法,在其中引入了阻尼因子,结合了高斯-牛顿法和梯度下降法的优势。
(2)研究分析不同应力水平下G1(σ)与G2(t)的规律性和一致性,判断其与本构方程的匹配度,确定适用于所有应力水平的方程参数。
(3)比较分析各方程与试验数据的拟合程度,最终确定适用于推进剂的蠕变本构方程。
3 蠕变本构方程的适用性
蠕变是时间相关的非线性过程,蠕变本构方程形式多样,数学特征具有异同性。针对不同方程,采取不同的策略,研究方程的推进剂适用性。
3.1 幂律类型蠕变本构方程
此类蠕变本构方程的特点是,通过对蠕变方程积分、移项、合并等处理方式,可将本构方程化为εcr=atb形式,且b为常数,a为σ的幂函数形式。
(1)应变硬化方程
(3)
对方程进行积分、移项、合并等处理,方程可化为
(4)
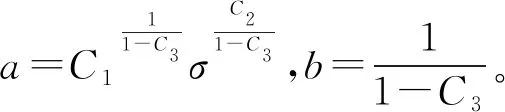
(2)时间硬化方程
(5)
对方程进行积分、移项、合并等处理,方程可化为
(6)
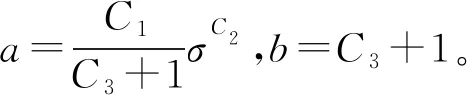
(3)改进时间硬化方程
(7)
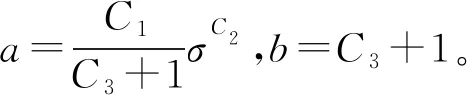
(4)改进应变硬化方程
(8)
对方程进行积分、移项、合并等处理,方程可化为
εcr=C1σC2(C3+1)C3tC3+1
(9)
于是,a=C1(C3+1)C3σC2,b=C3+1。
确定各方程a、b的具体形式,再针对各应力水平的蠕变试验进行数据拟合,确定适用于各自应力水平的a、b值,结果如表3所示。
为统一描述各应力水平的蠕变过程,结合各组试验数据拟合a与σ的函数关系,结果为
a=0.02042×σ2.63112,R2=0.94306
其中,R2为决定系数,表征回归分析的拟合程度,其值越接近1,则模型拟合度越高。R2接近1,表明a与σ的函数关系满足蠕变本构方程要求,幂律类型蠕变本构方程适用于此推进剂蠕变过程。
上述四种方程最终参数结果如表4所示。最终拟合曲线与试验数据对比如图4所示,拟合值与试验值的残差平方和RSS如表5所示。

表4 幂律类方程各参数值
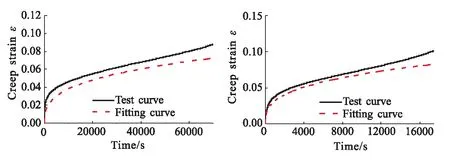
(a)σ=0.4 MPa (b)σ=0.5 MPa

表5 幂律类方程拟合值与试验值残差平方和
需要指出的是,幂律类各蠕变方程在物理意义与方程形式上存在明显差异,但由于各方程均能化为时间的幂函数形式,最终拟合曲线具有相同结果。结果表明,幂律类蠕变方程拟合曲线与试验曲线虽有一定偏差,但趋势一致性较好,能够反映蠕变过程。
3.2 广义指数蠕变本构方程
对原方程进行积分、移项、合并等处理方式,可将方程化为
εcr=-C1σC2e-rt+B
r=C5σC3e-C4/T
(10)
对于某组应力水平的蠕变试验,应力相关项为定值,上式等价于
εcr=-Ae-rt+B
r=C5σC3e-C4/T
(11)
式中A=C1σC2。
对各应力水平的试验数据进行拟合,确定A、B的值,如图5所示。根据图5,拟合计算A=C1σC2中C1、C2的值,拟合结果为A=0.11396×σ0.62424,R2=0.2821。
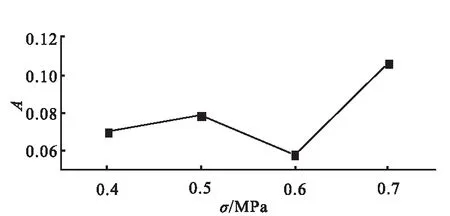
(a)Values of A
关于A=C1σC2的拟合计算中,R2远小于1,故A无法满足A=C1σC2函数条件,广义指数蠕变本构方程不适用于此推进剂的蠕变过程。
3.3 广义格雷厄姆蠕变本构方程
对原方程进行积分,并取C8=0,可化为
(12)
于是,可简写为
εcr=atb+ctd+etf
(13)
其中
根据已有经验和相关文献[15],取b=0.2,d=1,f=2,针对各应力水平的蠕变试验数据进行拟合,确定a、c、e的值,如表6所示。

表6 广义格雷厄姆方程的a、c、e的值
根据a、c、e与应力的幂函数关系,对表中数据进行幂函数拟合,结果如下:
a=1.1149×10-2×σ0.45845,R2=0.56025
c=2.2045×10-3×σ0.45845,R2=0.13102
e=-3.5289×10-9×σ0.45845,R2=0.11934
三个中间量的关于幂函数拟合计算的决定系数R2均远小于1,故a、c、e不具备应力的幂函数关系,说明此广义格雷厄姆方程不适用于推进剂的蠕变过程。
3.4 稳定阶段蠕变本构方程
蠕变过程根据蠕变应变率的变化,划分为三个阶段。蠕变第二阶段蠕变率相对恒定,称为稳定阶段。稳定阶段蠕变本构方程只针对于蠕变第二阶段,描述蠕变第二阶段蠕变率与应力水平的关系,即蠕变-时间曲线中稳定阶段的斜率与应力的关系。
(1)广义伽罗伐洛方程
(14)
(2)指数方程
(15)
(3)诺顿方程
(16)
式中 温度相关项的参数取为0,则式(14)式~(16)均为关于应力的函数。
针对各应力水平的蠕变试验,确定其稳定阶段的斜率,再根据斜率对以上三方程进行数据拟合,拟合结果如图6所示。结果表明,三种方程均能描述蠕变稳定阶段的斜率变化趋势。
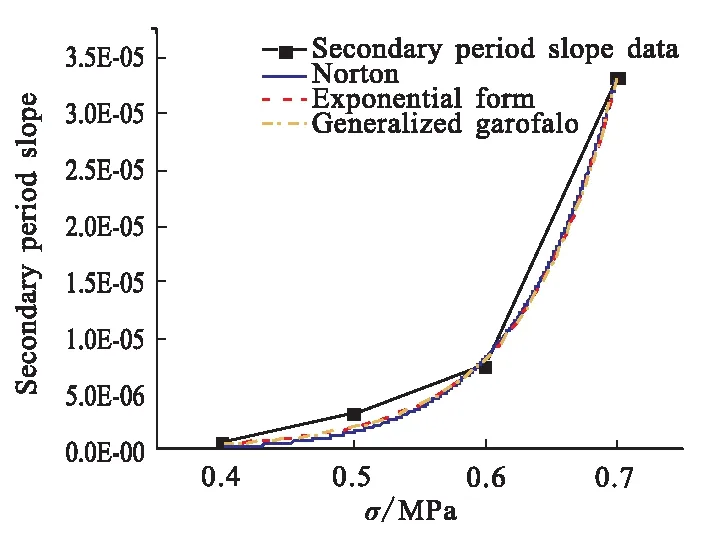
图6 第二阶段斜率的拟合曲线Fig.6 Fitting curves of secondary period slopes
图7为三种方程拟合结果与蠕变试验数据的对比结果。三种方程均能描述蠕变稳定阶段,但不具备描述蠕变初始阶段的能力。本文研究的是描述蠕变前两阶段的蠕变方程,故此类方程不适用于推进剂的蠕变过程。但在具体应用过程中,若确定推进剂的蠕变过程处在第二阶段,可考虑采用以上三种方程。
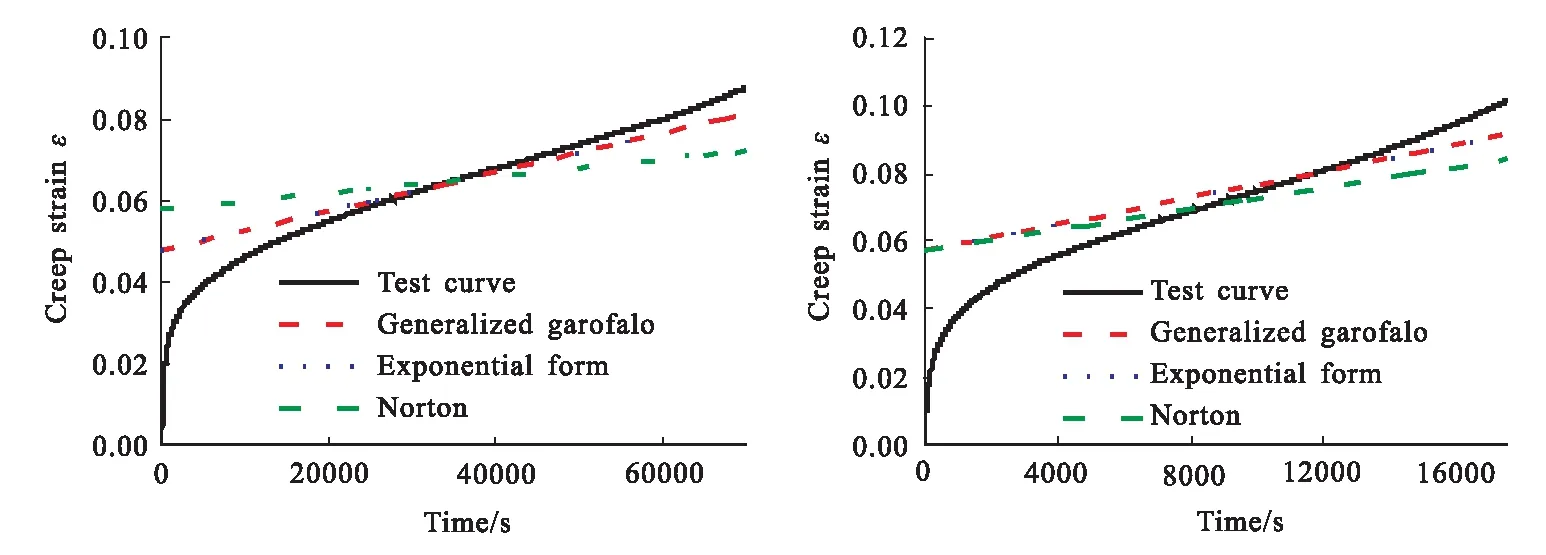
(a)σ=0.4 MPa (b)σ=0.5 MPa
3.5 复合时间硬化蠕变本构方程
(17)
复合时间硬化蠕变本构方程无需进行积分处理,温度相关项参数取为0,即C4=0、C7=0。对于某应力水平的蠕变试验而言,式(17)可写为
εcr=AtB+Ct
(18)

针对各应力水平拟合确定A、C的值,再确定A、C与应力的幂函数关系,结果如下:
A=0.01351×σ1.64377,R2=0.99383
C=0.0172×σ18.82979,R2=0.99645
其中,R2均接近1,表明A、C与σ的函数关系满足蠕变本构方程要求,复合时间硬化蠕变本构方程适用于此推进剂蠕变过程。最终结果如表7及图8所示。

表7 复合时间硬化蠕变本构方程系数值
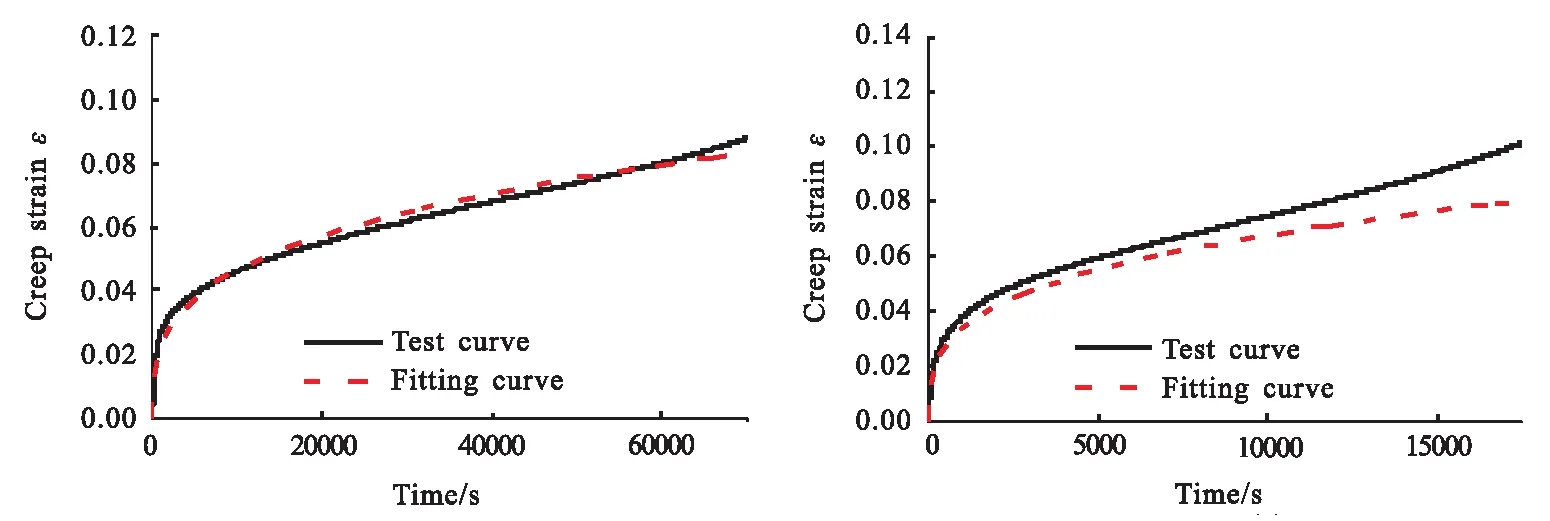
(a)σ=0.4 MPa (b)σ=0.5 MPa
最终拟合曲线与试验数据对比见图8,拟合值与试验值的残差平方和RSS如表8所示。结果表明,复合时间硬化蠕变本构方程拟值线与试验数据偏差最小,拟合曲线与试验曲线一致性最好,复合时间硬化蠕变本构方程能够很好地描述推进剂的蠕变过程。

表8 复合时间硬化蠕变本构方程拟合值与试验值残差平方和
3.6 有理多项式蠕变本构方程
有理多项式蠕变本构方程具有极其复杂的形式,本文对其简化形式进行研究。对方程积分简化后:
(19)
根据各应力水平的蠕变试验数据确定C、b、p值,再研究分析C、b、p与应力的关系。C、b、p结果如图9所示。

(a)Values of C
基于上述数据,拟合确定C、b、p与应力的幂函数关系:
C=5.887×10-2×σ0.3606,R2=0.6092
b=8.0202×10-4×σ9.2175,R2=0.9938
p=1.99×10-2×σ2.5639,R2=0.9788
结合图形与计算结果表明,关于C的幂函数拟合计算的决定系数R2<<1,不具备此有理多项式蠕变本构方程要求的幂函数形式,此方程不适用于推进剂的蠕变过程。
3.7 广义时间硬化蠕变本构方程
对于某应力水平的蠕变试验以及常温条件,原方程可简化为
εcr=ftr
(20)
式中f=C1σ+C2σ2+C3σ3;r=C4+C5σ。
针对各应力水平,拟合确定f、r的值,进一步确定f、r与应力的关系,结果如下:
f=0.02756×σ-0.07577×σ2+0.07208×σ3
R2=0.92548
r=0.19786+0.2221×σ,R2=1
其中,R2均接近1,表明f、r与σ的函数关系满足蠕变本构方程要求,广义时间硬化蠕变本构方程适用于此推进剂蠕变过程。最终确定所有参数的值,结果如表9所示。

表9 广义时间硬化蠕变本构方程系数值
最终拟合曲线与试验数据对比如图10所示,拟合值与试验值的残差平方和RSS如表10所示。结果表明,广义时间硬化蠕变本构方程拟合值与试验数据偏差大于幂律类方程与复合时间硬化方程,但在0.4、0.6、0.7 MPa下的偏差小于幂律类方程,拟合曲线与试验曲线一致性较好,广义时间硬化蠕变本构方程能够较好地描述推进剂的蠕变过程。
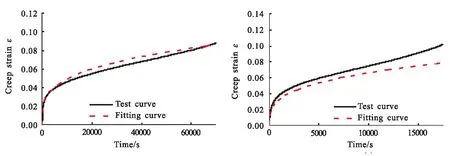
(a)σ=0.4 MPa (b)σ=0.5 MPa

表10 广义时间硬化蠕变方程拟合值与试验值残差平方和
4 结论
本文针对某配方HTPB推进剂发动机的立式贮存问题,开展了多应力水平的蠕变试验。根据试验数据,研究拟合了多种蠕变本构方程,并对各种蠕变的本构方程的适用性进行了研究。结论如下:
(1)开展了某配方HTPB推进剂试件的蠕变试验,获取蠕变数据。试验结果表明,HTPB推进剂的蠕变过程符合蠕变一般规律。
(2)对多种蠕变本构方程进行研究:幂律类型蠕变本构方程、复合时间硬化蠕变本构方程和广义时间硬化蠕变本构方程均适用于HTPB固体推进剂的蠕变过程。其中,复合时间硬化蠕变本构方程的拟合结果与试验数据误差最小。
(3)幂律类蠕变本构方程的拟合曲线与试验曲线在各应力水平都具有较好的一致性,能够反映HTPB固体推进剂的蠕变过程,且形式简单、处理方便,可在初步分析或特定应力水平下使用。本文研究成果可用于固体发动机立式贮存问题的仿真分析,为预示发动机立式贮存过程的蠕变效应提供指导。
