比较·融通·提升
2020-05-12佘路祥
佘路祥
摘要:如果说新授课是“画龙”,那复习课就是“点睛”。复习课不再是一个个分散独立的知识点的教学,而要去寻找这些知识点之间的联系,连点成线,织线成网,挖掘知识背后隐含的数学思想方法,形成整体建构。苏教版小学数学五年级上册《多边形的面积计算》单元复习课教学,可以分为三个阶段:整理比较、融会贯通、巩固提升。
关键词:小学数学复习课《多边形的面积计算》
对小学数学教师来说,上好复习课无疑是一种挑战,又无法回避。如,苏教版小学数学教材五年级上册共安排了64课时的教学内容,其中有11课时为复习课(实际教学中,复习课课时一般更多),单元结束后有单元复习,所有新课结束后还有总复习。
复习课不再是一个个分散独立的知识点的教学,而要去寻找这些知识点之间的联系,连点成线,织线成网,挖掘知识背后隐含的数学思想方法,形成整体建构。所以,复习课不能贪多求全,简单地再现新授课所学的内容,进行低水平的重复。苏教版小学数学五年级上册《多边形的面积计算》单元复习课教学,可以分为三个阶段:整理比较、融会贯通、巩固提升。
一、整理比较阶段
(一)知识梳理
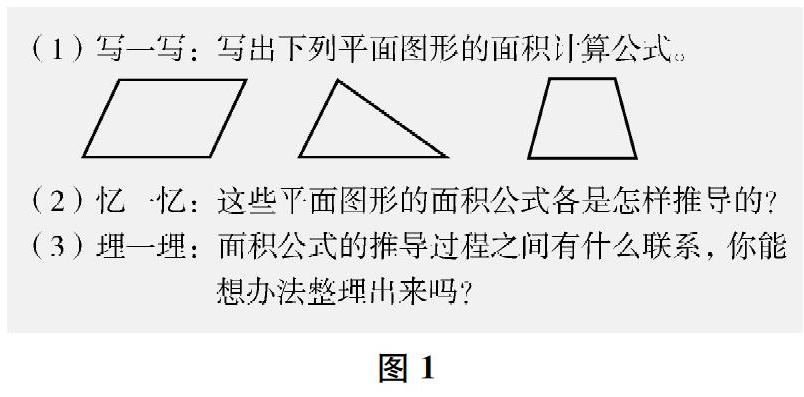
课前,教师布置学生对多边形的面积计算相关知识进行整理:可以让学生用条目式、板块式、导图式等形式进行自主整理;也可以提供“整理单”(如图1),让学生对照整理,引导学生再现所学知识,发现其间内在联系,初步形成整体认知。
(1)写一写:写出下列平面图形的面积计算公式。
(2)忆一忆:这些平面图形的面积公式各是怎样推导的?
(3)理一理:面积公式的推导过程之间有什么联系,你能想办法整理出来吗?
该“整理单”前两问答案相对固定;第(3)问则比较开放,意在促使学生寻找不同图形面积公式推导过程之间的联系。
(二)联系比较
数学是一门研究关系的学科。小学数学复习课中,教师应特别重视引导学生用联系的观点看问题,比较不同知识之间的相似和区别,增强系统观念和思辨意识。
上课伊始,教师让学生组内交流自己的“整理单”,小组形成共识后再在班级展示。在生生互动、师生互动中厘清认识、明晰关系后,教师带领学生就“整理单”第(3)问进行比较——
生(展示图2)通过整理我们可以发现,从长方形的面积公式可以推导出平行四边形的面积公式,从平行四边形的面积公式可以推导出三角形和梯形的面积公式。由此可见,长方形的面积公式是推导其他平面图形面积公式的源头。
生(展示图3)我们组发现,推导平行四边形的面积公式时,可以把平行四边形转化成长方形来研究;推导三角形和梯形的面积公式时,可以把它们转化成平行四边形来研究。即长方形的面积公式是转化的根。
师转化是一种重要的数学思想。我们在研究新的图形的面积计算时,可以把它转化成已经学过的图形,根据两个图形之间的联系,推导出新的图形面积计算的方法。观察平行四边形到长方形的转化与三角形、梯形到平行四边形的转化,它們有什么不同呢?
生平行四边形通过剪、移、拼转化成长方形后,面积没有发生变化;三角形和梯形都是用两个完全一样的图形拼成平行四边形的,拼成的平行四边形的面积是原来图形面积的2倍。
师平行四边形转化成长方形,面积没有变化,这种转化我们可以称为“等积转化”;三角形、梯形转化成平行四边形,面积变成了原来的两倍,这样的转化我们可以称为“扩倍转化”。
二、融会贯通阶段
(一)温故知新
复习课不能简单地理解为“知识梳理+配套练习”,而应着眼于学生的思维提升,做到“温故而知新”,让不同的学生在复习课上都能得到“生长”。
对不同的转化方式归类后,教师要求学生用“等积转化”的方式推导三角形的面积计算方法。另辟蹊径而殊途同归,呈现的是方法多样化,收获的是思维创造性。具体教学片段如下——
师三角形、梯形也能通过“等积转化”的方式推导出面积计算方法吗?我们先来研究三角形。(出示活动要求,见下页图4)为了方便研究,我们把三角形放到方格纸中,请完成这一活动。
(学生活动后展示汇报。)
生(展示下页图5)我把三角形转化成平行四边形:它们的面积相等,平行四边形的底是三角形的底,平行四边形的高是三角形高的一半。因为平行四边形的面积=底×高,所以三角形的面积=底×(高÷2)=底×高÷2。
生(展示图6)我也把三角形转化成平行四边形:平行四边形的底是三角形底的一半,平行四边形的高就是三角形的高。因为平行四边形的面积=底×高,所以三角形的面积=(底÷2)×高=底×高÷2。
生(展示图7)我把三角形转化成长方形:它们的面积相等,长方形的长是三角形的高,长方形的宽是三角形底的一半。因为长方形的面积=长×宽,所以三角形的面积=高×(底÷2)=底×高÷2。
师同学们运用多种“等积转化”的方法都探索出了三角形面积的计算方法,转化时都不约而同地用到了三角形边上的中点。用这样的思路,你能探究梯形的面积计算公式吗?
(学生讨论后展示交流。)
(二)发展图式
图式是人脑中已有的知识经验的网络,表征特定概念、事物或事件的认知结构。学生原有的图式有没有得到发展,是数学复习课应该深入考虑的问题。
本节课复习到这里,学生运用转化的思想推导平面图形面积计算公式的方法在原有的基础上更加丰富:三角形不仅可以转化成平行四边形,也可以转化成长方形;梯形不仅可以转化成平行四边形,也可以转化成三角形或长方形。这时的图式已基本形成,能不能再次刷新学生的认知,构建新的图式呢?可以做如下一些尝试——
师(课件演示梯形变成三角形的动态过程,如图8)现在梯形变成了什么图形?上底是多少?下底是多少?面积公式会怎样变化?
生梯形变成了三角形,上底变成了0,下底变成了三角形的底,面积=(0+下底)×高÷2=底×高÷2。梯形的面积公式变成了三角形的面积公式。
师(课件演示梯形变成平行四边形的动态过程,如图9)这时梯形变成了什么图形?上底、下底发生了怎样的变化?面积公式又会怎样变化?
生梯形变成了平行四边形,上底和下底一样长,都是平行四边形的底,面积=(上底+下底)×高÷2=底×2×高÷2=底×高。梯形的面积公式变成了平行四边形的面积公式。
师(课件演示梯形变成长方形的动态过程,如图10)这时梯形变成了什么图形?上底、下底发生了怎样的变化?面积公式又会怎样变化?
生梯形变成了长方形,上底和下底一样长,就是长方形的长,高变成了长方形的宽,面积=(上底+下底)×高÷2=长×2×宽÷2=长×宽。梯形面积公式变成了长方形面积公式。
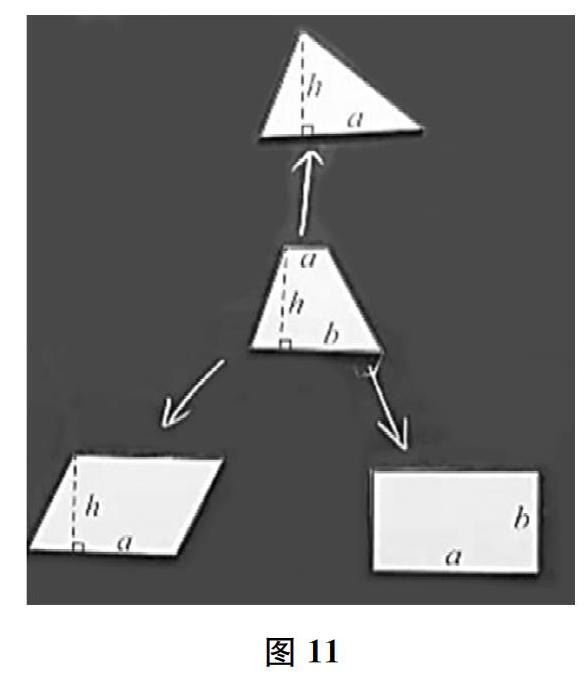
师原来梯形的面积公式可以解释三角形、平行四边形和长方形的面积公式,它真是一个万能公式!所以,(同步板贴,如图11)我们可以得到这样的关系图。看似相互独立的知识点间,实际上有着千丝万缕的联系,这就是数学的迷人之处。
三、巩固提升阶段
一节复习课的效果怎么样,需要通过相应的练习来检验,看学生是否已达到巩固基础、举一反三、灵活应用的要求。我们可设计基础题、变式题、拓展题,供学生分层练习、闯关冲刺;而练习的时间必须充分,以确保课上不仅有练习,而且有反馈。
本节复习课的核心是转化思想的渗透。学生解决图形面积问题时能否自觉运用转化的思想,可以通过如下练习来检测:
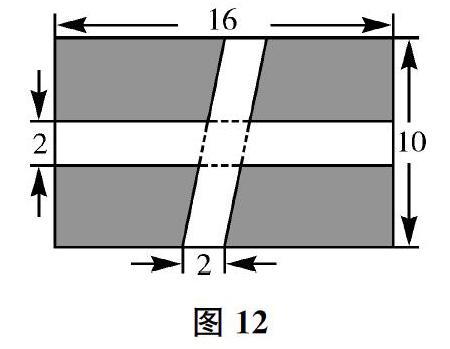
1.如图12所示,有一块长方形草地,长16米,宽10米,中间有两条小路,一条是长方形的,一条是平行四边形的,求草地部分的面积。
2.图13是两个完全一样的直角三角形重叠在一起,求涂色部分的面积(单位:厘米)。
如果说新授课是“画龙”,那复习课就是“点睛”。要真正上好小学数学复习课,需要我们研究教材、研究学生,在教学实践中不断探索,总结经验,因材施教,灵活运用,用数学思想指引学生比较、融通、提升。
