对“发现问题”和“提出问题”的一点认识
2020-05-12陈云
陈云

摘要:当前,培养学生发现和提出问题的能力已经得到一线教师的普遍认可,但在实际教学中,还存在着诸多片面理解和流于形式的弊端。发现问题和提出问题不是一个简单的“看见”和“发问”的过程。发现问题是指,在错综复杂的数学情境或生活情境中,用数学的眼光进行分析,并且能够从中发现自己的困惑,形成自己的质疑。提出问题是指,对自己发现的问题进行整理、提炼,将内部语言外部化,将现实问题数学化,形成清晰、有条理的数学表述。
关键词:数学问题发现问题提出问题创新
《义务教育数学课程标准(2011年版)》将课程总目标由传统的“双基”变为“四基”,由原有的两个能力(分析和解决问题的能力)变为四个能力(增加了发现和提出问题的能力)。之所以做出这样的改变,是因为长期以来“以知识为本”的教育理念使得发现和提出问题能力的培养成为我国基础教育的薄弱环节,进而导致很难培养出当今社会急需的创新型人才。当前,培养学生发现和提出问题的能力已经得到一线教师的普遍认可,但在实际教学中,还存在着诸多片面理解和流于形式的弊端。
一、何为数学问题
不管是发现问题还是提出问题,首先都要弄明白什么是数学问题。有些教师认为,有提问的就是数学问题,有未知量的就是数学问题,需要学生解答的就是数学问题。例如,学生学习了“100以内的加减法”之后,教师结合具体情境给出了这样的问题:
运动会已经到了最后的准备时间,今天在操场上参加训练的男生有58人,女生有39人,请问:操场上参加训练的一共有多少人?参加训练的男生比女生多多少人?
一些教师认为这就是一个数学问题。事实上,答案是否定的!请看一下前提条件:学生已经学习了100以内的加减法。这里,学生只需要运用已有的知识和经验,就能够解决问题。这只是对原有知识和技能的巩固,不需要寻求新的路径和方法。因此,这里的问题只是教师给学生提供的一个“练习”,不是我们所指的“数学问题”。
那么到底什么才是数学问题?孔凡哲、曾峥编著的《数学学习心理学(第2版)》中指出:“数学问题是指不能用现成的数学经验和方法解决的一种情景状态。这里的问题即problem,而不是question。”也就是说,所谓的“数学问题”,应该是学生的一种困惑、质疑,能激发学生进一步探索。对于数学问题,学生不能直接看出答案,不能直接用现成的数学知识解答,需要深入研究与思考,需要采用新的策略、认知等去解决。而这些新的策略、认知等就是我们通常所说的新知(或新的教学内容)。例如,针对上述问题情境,教师可以追问:
体育组的张老师又带来128名要在开幕式上进行体操表演的同学,请问:这时候操场上共有多少名同学?
显然,这里的计算不再是100以内的加减法了。这是学生初次遇到的新问题。学生有了困惑:怎么解答?开始质疑:和100以内的加法计算有什么不同?形成猜想:可不可以把数拆开来算一算或者试着列竖式解答?……像这样能激发学生运用“已知”探索“未知”的问题,才是我们所说的“数学问题”。可见,数学问题应该符合这样两个特点:(1)能给学生造成思维上的障碍;(2)能够激起学生的探究欲望。
二、何为发现问题
发现问题是指,在错综复杂的数学情境或生活情境中,用数学的眼光进行分析,并且能够从中发现自己的困惑,形成自己的质疑。没有经过自主思考,没有感到困惑、提出质疑,就不能算发现问题。
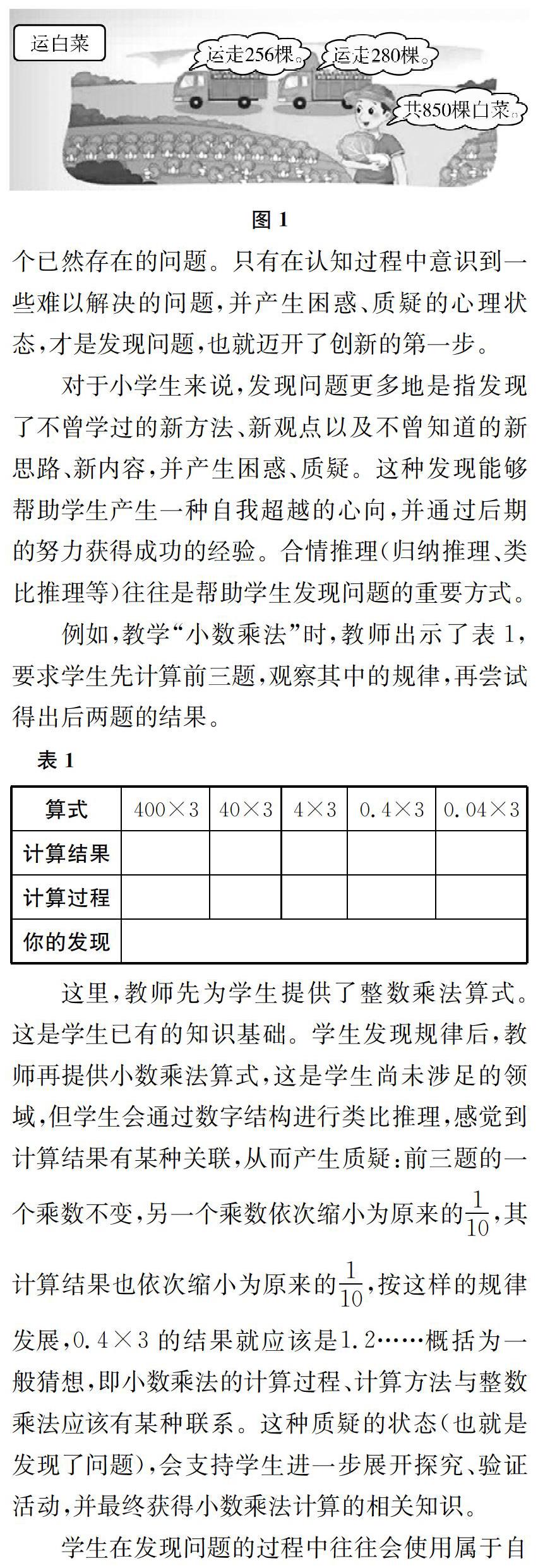
例如,教学“1000以内数的连加连减”时,教师创设了如图1所示的情境,并问学生发现了什么问题。学生回答:“共有850棵白菜,运走了256棵,又运走280棵,还剩多少棵白菜?”
这是发现问题吗?显然不是。发现问题应该是一种复杂的心理状态,不能等同于“看见”了一个已然存在的问题。只有在认知过程中意识到一些难以解决的问题,并产生困惑、质疑的心理状态,才是发现问题,也就迈开了创新的第一步。
对于小学生来说,发现问题更多地是指发现了不曾学过的新方法、新观点以及不曾知道的新思路、新内容,并产生困惑、质疑。这种发现能够帮助学生产生一种自我超越的心向,并通过后期的努力获得成功的经验。合情推理(归纳推理、类比推理等)往往是帮助学生发现问题的重要方式。
例如,教学“小数乘法”时,教师出示了表1,要求学生先计算前三题,观察其中的规律,再尝试得出后两题的结果。
这里,教师先为学生提供了整数乘法算式。这是学生已有的知识基础。学生发现规律后,教师再提供小数乘法算式,这是学生尚未涉足的领域,但学生会通过数字结构进行类比推理,感觉到计算结果有某种关联,从而产生质疑:前三题的一个乘数不变,另一个乘數依次缩小为原来的110,其计算结果也依次缩小为原来的110,按这样的规律发展,0.4×3的结果就应该是1.2……概括为一般猜想,即小数乘法的计算过程、计算方法与整数乘法应该有某种联系。这种质疑的状态(也就是发现了问题),会支持学生进一步展开探究、验证活动,并最终获得小数乘法计算的相关知识。
学生在发现问题的过程中往往会使用属于自己的,不完整、不连贯的,具有高度情境性的语言。这时,教师要引导学生尽可能把这种“内部语言”转化为“外部语言”,理清思考过程中每一个判断的理由和依据,使思考过程清晰、有条理,逐渐形成数学语言,从而为提出问题奠定基础。
三、何为提出问题
提出问题是指,对自己发现的问题进行整理、提炼,将内部语言外部化,将现实问题数学化,形成清晰、有条理的数学表述;不能理解为简单的“发问”。
例如,教学“三位数乘两位数”时,教师创设了如图2所示的情境,并问学生:“根据图中信息能够提出哪些数学问题?”学生回答:“卫星绕地球2圈需要多少分钟?”“卫星绕地球3圈需要多少分钟?”“卫星绕地球4圈需要多少分钟?”……最后,教师“忍不住”自己来提出问题:“卫星绕地球21圈需要多少分钟?”这才终于引出本节课的内容。
可见,对于小学生来说,提出问题不仅需要逻辑推理,还需要教学抽象,在错综复杂的信息中抓住问题的核心,进行条分缕析的陈述。这实在是一件不简单的事。
总之,不论“发现问题”还是“提出问题”,都必须深入思考和组织,诱发智慧和灵感,找到疑难。这与跟着教师去验证、推断既有的结论是不同的思维方式。只有在这样的思维方式训练下,学生才能逐渐形成创新精神,提升创新能力。
参考文献:
[1] 孔凡哲,曾峥.数学学习心理学(第2版)[M].北京:北京大学出版社,2012.
[2] 史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京:高等教育出版社,2013.
[3] 史宁中,柳海民.素质教育的根本目的与实施路径[J].教育研究,2007(8).管理智慧
