信息学科中程序填空问题的解题技巧探究

摘 要：信息学科中程序填空题阅读量巨大，学生需要耗费大量时间来理解题意，而近几年对计数思想的考查，更标志着程序填空题的难度从代码层面到思维深度的跨越。笔者经过对程序填空题的研究归纳，总结出六点解题技巧，让学生尽快理解出题人设计意图及算法核心思想，提高解题效率。

关键词：计数思想;筛法求质数;有效思考

浙江省2017年4月份信息技术选考卷第17题中，考查了计数思想的应用，而计数排序并没有作为一个专门的内容在信息学科指导意见中出现，我们通过分析这道加试题来了解计数思想的算法思想。

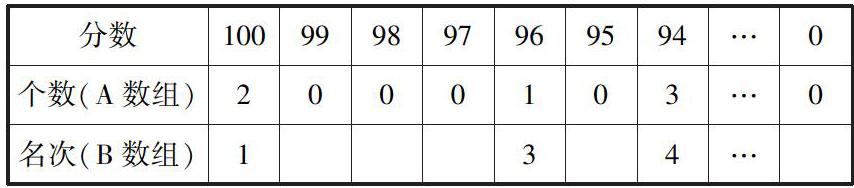
【加试题】小王编写了一个依据成绩计算名次的VB程序，成绩为0到100之间的整数。算法的基本思想：先统计每个分数的个数，然后按照分数从高到低依次计算每个有效分数（该分数的个数不为0）对应的名次，分数相同时名次并列。最高分为第1名，该分数的名次与个数之和为下一个有效分数的名次，以此类推。程序用数组A存放每个分数对应的个数，数组B存放每个分数对应的名次。例如，下表中最高分100有2个，并列第1名，则分数96的名次为分数100的名次加上分数100的个数，即第3名。

程序运行时，学生数据显示在列表框List1中，单击“计算”按钮Command1，计算结果显示在列表框List2中，程序运行界面如图所示。

实现上述功能的VB程序如下，请回答下列问题：

（1）如表所示，若分数93的个数为2，则该分数对应的名次为  。

（2）请在画线处填入合适的代码。

Dim sName（ 1 To 50 ） As String 存放学生姓名

Dim sScore（ 1 To 50 ） As Integer 存放学生分数

Dim recCount As Integr 存放学生人数

本过程从数据库中读取学生数据，存储在相应的变量中，并在List1中显示，代码略

整数转换成长度固定的字符串

Function ads（ x As Integer ， n As Integer ） As String

Dim sx As String ， nx As Integer ， i As Integer

sx = Str（x） ： nx = Len（sx）

For i = 1 To n - nx

sx= ″ ″ + sx

Next i

①

End Function

Private Sub Command1_Click（）

Dim A（ 0 To 100 ） As Integer ， B（ 0 To 100 ） As Integer 存放每個分数的个数和名次

Dim mc As Integer ， score As Integer ， i As Integer

For i = 0 To 100

A（i） = 0

Next i

For i = 1 To recount 计算每个分数的个数

②

Next i

mc = 1

For i = 100 To 0 Step -1 计算每个分数的名次

If A（i） <> 0 Then

B（i） = mc

③

End If

Next i

List2.Clear ： List2.AddItem ″姓名分数名次″： List2.AddItem ″--″

For i = 1 To recCount

Score = sScore（i） ： mc = B（sScore（i））

List2.AddItem sName（i） + ads（score ， 5）+ ″第″ + ads（mc ， 3） + ″名″

Next i

End Sub

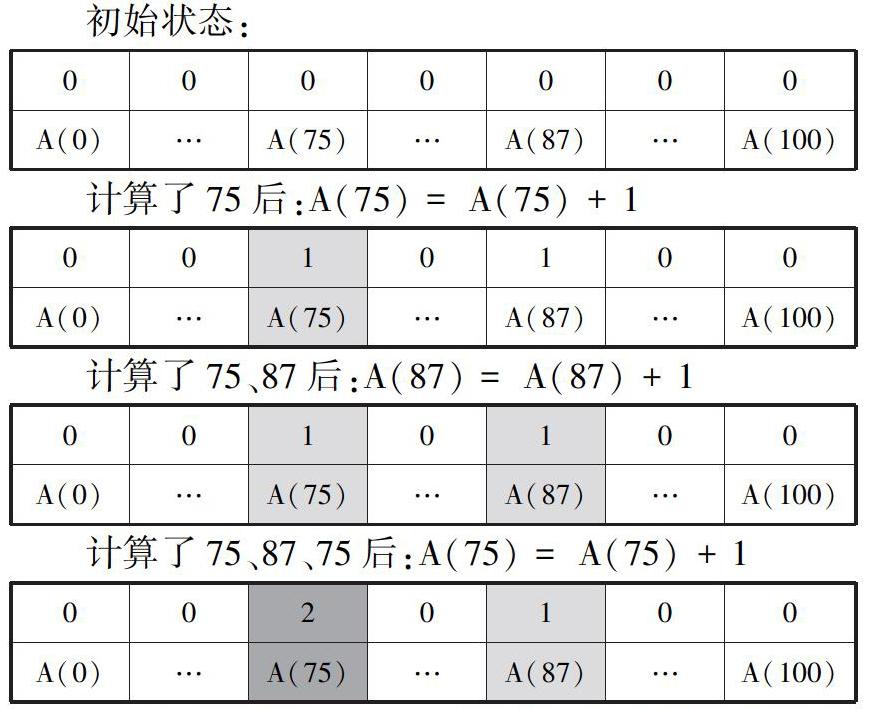
冒泡和选择排序是基于比较的排序，计数排序是基于元素键值的排序，其核心思想是将待排序关键字作为数组下标，将数组值表示为对应下标数字出现的次数。以本题为例，A（i）中的值表示分数i出现的次数，其初始值为0，表示在排序开始时每一个分数都未出现过，再枚举每个学生的分数，表示该分数出现了一次，将该分数对应的计数加1，故②处应填入A（sScore（i）） = A（sScore（i）） + 1，此空也是计数排序核心思想的体现。

假设只有三个学生，其分数分别为75、87、75，则每次A数组的变化过程如下：

此时如果我们需要对三个学生的成绩按照从大到小排序的话，我们只需要从100（分数的上界）枚举到0（分数的下界），第一个遇到非0的A（i）为A（87），其值为1，表示出现了一个87。其后还有两个75，则排序后的结果为87、75、75。

而此题还要计算每个分数的排名，我们只需将相应的排名变量对A（i）做一个累加即可，即第③处的答案为mc = mc + A（i）。第①处考查的是VB中函数返回值的使用，答案为ads = sx。

计数排序算法于1954年由Harold H. Seward提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο（n+k）（其中k是整数的范围），快于任何基于比较的排序算法。当然这也是算法设计中，以牺牲空间为代价来提高时间效率的一种常见处理方法。

近几次技术选考中，也出现过求质数的应用，包括判断一个数是否是质数以及预处理出一定范围的质数。判断一个数是否为质数问题主要考查学生对枚举算法的掌握情况以及数的整除问题的一个简单应用，而求出一定范围内的质数时，常使用筛法求质数，也是计数思想的一种应用。假设需求出1000000以内的所有质数，其算法主要过程如下。

一、 定义布尔型数组f[1 to 1000000]，f[i]表示i是否为质数。

二、 将f数组初始化为true，预设每个数都是质数。

三、 i从2开始枚举到1000000，如果f[i]等于true，则f[i]是质数，且所有i的倍数都不是质数，将f[i的倍数]赋值为false。如果f[i]等于false，则直接枚举下一个i。

四、 当i枚举结束，此时f数组中值为true的数是质数，反之不是质数。当然1为特殊情况，需要特判。

观察以上算法，易发现在计数思想中需要使用额外的辅助存储空间，其空间范围为待统计数值的大小，即如果数值过大，则程序无法申请对应的空间，即使空间足够，逐个枚举每个元素也会导致程序运行过慢。因此我们需要根据题目给定的数据规模与限制条件来选择合适的算法来解决问题。

计数思想的考查，标志着技术科目选考的考查内容从传统的选择排序，冒泡排序，二分查找等常见算法框架提升到对变量、数理逻辑思维等更深层次的领域，作为整张卷子的压轴题，考查内容也更为灵活。而在考场上，程序填空题往往题目描述及代码阅读量都非常大，部分学生仅仅为了读懂题目就耗费了大量的时间，哪怕最后勉强读懂，仓促拿分，也会导致后面的通用模块来不及解答。笔者经过对程序填空题的研究归纳，結合其特点，总结出以下六点思考技巧，让学生在短时间内尽量摸准算法核心思想，提高正确率。

一、 了解输入输出内容。

二、 确定核心变量含义。

三、 变量使用前需要初始化。

四、 初始化后的变量大概率是要被使用的。

五、 循环的初始和结束条件。

六、 函数的返回值是否符合要求。

带着以上六点去思考，可以让学生有针对性地考虑问题，减少无效思考时间，在短时间内做出正确的解答。下面再结合一个例题进行讲解：

小明编写了一个字符串加密程序，功能如下：在文本框Text1中输入明码，单击”加密”按钮Command1后，在文本框Text2中显示加密后的密文。加密算法如下。

（1）将明码中每个字符的八位二进制ASCII码（不足八位的左端补0，凑足八位）分成两段（高4位一段，低4位为另一段），如大写字母“C”的二进制ASCII值为01000011，分段后为0100，0011。

（2）将高位段（左边4位）左移一位，并将4位里原最高位移到最低位处（如0100左移后为1000），再转化为十六进制数（如1000转化为8）。

（3）对低位段（（右4位）按2）所示转化，如0011→0110→6。

（4）顺次连接两位十六进制数，得到该字符的暗码，如“C”的暗码为“86”。

（5）将每个字符的暗码按照明码的顺序连接。

实现上述功能的VB程序如下，请在画线处填入合适代码。

Private Sub Command1_Click（）

部分变量定义

Dim d（ 1 To 8 ）As Integer 数组d存储字符ASCII码二进制从左到右的各位数码

Dim mw As String mw存储暗码

mw = ″ ″

For i = 1 To Len（Text1.Text）

c = Mid（Text1.Text， i， 1）

For j = 1 To 8

d（j） = 0

Next j

m = Asc（c）

①

Do While m > 0

d（k） = m Mod 2 ： m = m ＼ 2 ： k = k - 1

Loop

x = d（1） ： y = d（5）

For j = 1 To 3

d（j） = d（j + 1）

②

Next j

d（4） = x ： d（8） = y

mw = mw + btoh（d）

Next i

Text2.Text = mw

End Sub

以下函数是将数组元素中的二进制数转换成对应的十六进制数

Function btoh（ m（） As Integer ） As String 将数组m作为函数的参数

部分变量定义

str=″0123456789ABCDEF″ ： s = 0 ： ch = ″ ″

For i = 1 To 8

s = s * 2 + m（i）

If i = 4 Then ch = Mid（str， s+1， 1） ： s = 0

Next i

③

End Function

该题篇幅较长，且题面描述的五步加密算法非常复杂，如果从题目描述出发，再去揣摩出题人的代码对应的实际含义，非常费时。下面笔者尝试结合提出的六点思考技巧来解决此题。

首先快速通看全题，第③空相对独立，该函数要将m数组中的二进制转化成对应的十六进制数再通过函数值返回，观察函数段中并没有出现函数返回值处理，故此空显然是关于函数返回值的处理，即关于btoh的赋值语句。

而m中总共8位2进制数，对应2位十六进制数，且程序中在i = 4时对这两个十六进制数做了一个隔断，第一个数存在ch中，而i = 8时并没有额外处理，此时第2个十六进制数还在Mid（str， s+1， 1）中，故此处的答案只能为btoh = ch + Mid（str， s+1， 1）。

再观察第①空，注意到下方的while循环中，有一行代码为k = k - 1，而此时k并没有初始化，故大胆假设此处是关于k初值的赋值语句，结合代码段前后文中关于d数组下标的处理，此处的答案为k = 8。

题目需要处理的三个空中仅有第②空是关于占据了题目一大部分的加密算法的处理，观察x和y这两个核心变量的处理，易知第②空是处理剩余低位段那3位左移操作，且给出的d（j） = d（j + 1）也已经提醒和印证了我们的结论，故此空的答案为d（j + 4） = d（j + 5），由于规模不大，我们也可再将j代回来进行最后校验。至此，本题圆满解决。

在解决加试题的压轴题环节，我们可以通过强化对计数排序等侧重思维的算法训练，提高算法思维能力，也可通过面对具体题目时，带线索的针对性思考，尽可能绕开大篇幅的背景和代码描述，可以大大减少思考时间，减小题目的整体难度，在解决程序填空类问题时，达到事半功倍的效果。

参考文献：

[1]杨绣丞，李彤，赵娜，等.计算排序算法设计与分析[J].计算机应用研究，2014，31（3）：658-662.

[2]曹红霞.程序设计模块学业水平考试命题研究[J].中国信息技术教育，2014（23）：76-78.

作者简介：

李建，浙江省杭州市，浙江省杭州市杭州第二中学。